参数优化方法在AUV组合导航系统PQR调参中的工程应用

白 龙，彭荆明，吴 爽，吕志刚

(中国船舶集团有限公司第七一⚪研究所，宜昌443003)

0 引言

由于体积小、使用成本低、智能化自主作业、保障维护方便、隐蔽性好等诸多优点,自主式水下无人潜航器(Autonomous Underwater Vehicle,AUV)在海洋开发和国防领域正发挥着越来越重要的作用[1]。随着AUV应用领域的逐渐扩展,对导航系统的要求也越来越高,导航系统必须具备远航程和长航时的高精度导航定位能力[2-3],因为高精度导航定位决定着AUV能否安全作业及返回以及水下目标定位、海底地形测绘、水下定点布放等作业结果的准确性[4-5]。

为提高水下组合导航系统的定位精度,国内外诸多机构和学者从多个方面进行了探索。朱春云等[6]使用Kalman在线估计的方式来实现DVL三个安装误差角的实时估计；于玖成等[7]选取多点参考定位方法,利用GPS系统测量AUV的经纬度和速度信息来估计DVL和SINS的各项误差,从DVL标定方面[8-11]来提高水下组合导航系统的定位精度；Broatch等[12]、穆华等[13]利用分散化滤波中的联邦Kalman滤波,通过动态信息分配系数来优化各子系统的导航信息,以增强AUV的导航性能；魏延辉等[14]、Liu等[15]、付凤婷等[16]分别提出了基于自适应滤波、无迹Kalman滤波和迭代无迹Kalman滤波的水下组合导航系统,以期通过改进多传感器信息融合方法来进一步提高水下组合导航系统的定位精度。但是,在组成水下组合导航系统的INS、DVL、GPS等设备或传感器既定的前提下,如何保证多传感器信息融合[17-18]处于最佳状态以充分发挥出导航系统的整体性能,却很少有相关研究。本文针对由SINS/GPS/DVL构成的AUV组合导航系统,借鉴多学科优化设计思想,使用目标优化方法[19]对组合导航系统的系统参数进行整定,以期挖掘组合导航系统的极限性能,从而保证AUV获得最佳的水下组合导航定位精度。

1 方法原理

本文所研究的AUV组合导航系统采用SINS/GPS/DVL的组合导航方式,为载体提供连续且高精度的导航信息,其系统构成如图1所示。当在水下航行时,AUV使用SINS/DVL的组合导航方式。由于DVL测速误差的存在,水下组合导航系统的位置误差会随着时间不断积累,从而体现出定位误差随航程增加而线性增大的特点。故当AUV水下航行一定路程后,AUV通过上浮出水面或抛出浮标等方式来接收GPS信号,校正AUV当前位置,消除长时间水下导航所积累的位置偏差。校准完成后,AUV继续开展水下作业任务,这种状态即 “水下潜航→水面GPS校准→水下潜航”工作模式。

图1 AUV组合导航系统框图Fig.1 Block diagram of AUV integrated navigation system

1.1 AUV组合导航系统原理

4)当无外界量测信息时,惯导处于纯惯性模式,Kalman滤波器仅进行时间更新。

AUV组合导航系统的Kalman滤波过程如图2所示[21]。图2中,P0、Qk、Rk等系统参数需要根据陀螺和加速度计的性能指标结合工程经验进行设置。由于这些系统参数极大影响着Kalman滤波器的性能,往往需要经过手工调参给出一组合适的值,以使整个组合导航系统实现较理想的组合导航性能。

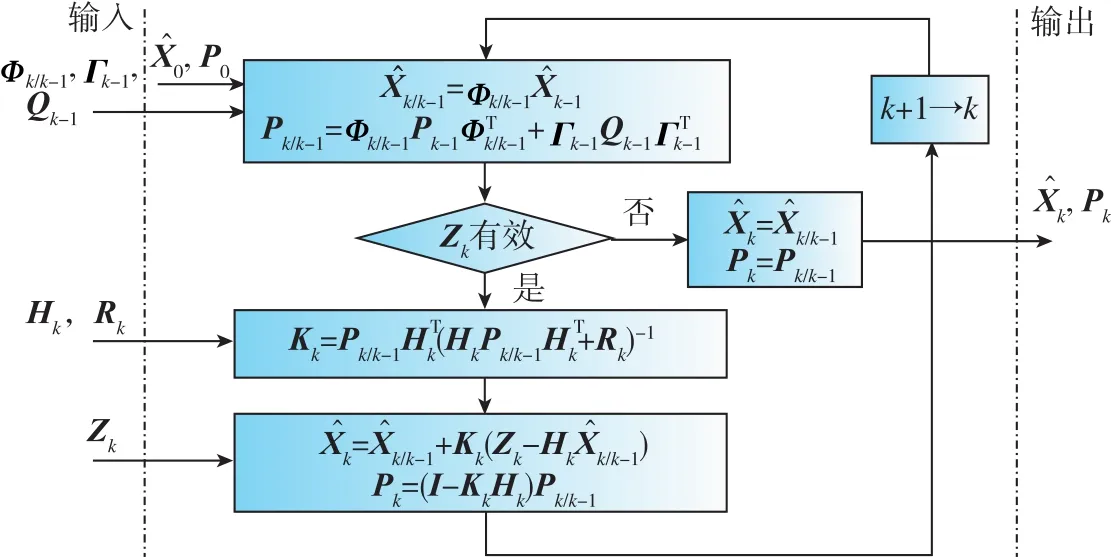
图2 Kalman滤波流程图Fig.2 Flowchart of Kalman filtering

1.2 基于目标优化方法的组合导航系统调参

本文借鉴多学科目标优化设计思想,如图3所示,将P0、Qk、Rk等系统参数视为自变量,几段直线航程的SINS/DVL组合导航的终点定位误差降至最小作为优化目标,通过目标优化算法和手段,来找到能够使终点定位误差实现最小的全局最优解,从而将AUV组合导航系统的系统参数调节问题转化为在几个自变量的各自值域范围内、在一定条件的约束下寻找全域内最优解的目标优化问题。

图3 目标优化问题示意图Fig.3 Schematic diagram of target optimization

(1)拉丁超立方抽样算法

拉丁超立方抽样[22](Latin Hypercube Sampling)是一种从多元参数分布中近似随机抽样的方法,属于分层抽样技术,常用于计算机实验或Monte Carlo积分等。在统计抽样中,拉丁方阵是指每行、每列仅包含一个样本的方阵。拉丁超立方则是拉丁方阵在多维中的推广,每个与轴垂直的超平面最多含有一个样本。

假设有n个变量(维度),可以将每个变量根据各自的取值范围分为m个概率相同的子区间,最后在每个子区间内分别进行独立的等概率抽样。此时,可以选出m个满足拉丁超立方条件的样本点。具体抽样步骤为:

1)将每一维分成互不重叠的m个区间,使得每个区间有相同的概率；

2)在每一维里的每一个区间中随机抽取一个点；

3)再从每一维的步骤2抽取的点集中随机抽取1个点,将它们组成一个解向量,步骤2每一维抽取的点集中被步骤3抽取过的点不再使用,最终抽取获得m个这样的解向量,即为由拉丁超立方算法抽样得到的样本点。

(2)单目标粒子群优化算法

类似于其他进化算法,单目标粒子群优化算法[23]也采用了群体、适应和进化的理念,通过个体间的协作,解决复杂空间中最优解的搜索问题。设d维解空间中存在由m个粒子组成的种群,每个粒子称为单个个体。第k个粒子在解空间中第j次迭代时的位置记为,在空间中以速度运动搜索,经历的最好位置为,则对于优化目标函数,种群中所有粒子经历的全局最优位置为

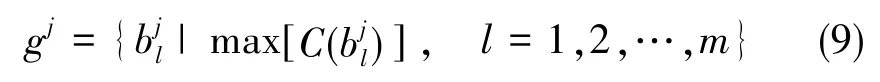
第k个粒子在进化中的速度和位置更新公式分别为

式(10)中,w为惯性权重系数,描述了粒子的惯性对速度的影响,可以通过调节该参数来平衡粒子群算法的全局搜索能力和局部搜索能力；c1、c2为加速度因子,用于调节算法的收敛速度,一般取值在1～2之间；σ1、σ2为[0,1]之间均匀分布的随机数。是粒子在每一次迭代后对自身的认识部分,描述了粒子的自我认知能力；是粒子向整个种群的学习部分,体现了粒子间的协作。第k个粒子经历的最好位置更新为

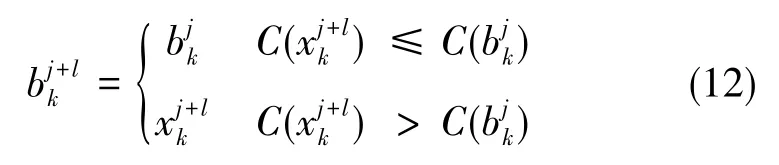
(3)具体实现方法

对于系统参数P0、Qk、Rk的调节问题,首先根据加速度计、陀螺、DVL和GPS的性能指标给出经验值P0、Qk、Rk；然后设置kp0、kQk、kRDVL、kRGPS这4个变量作为P0、Qk、Rk的调节系数,在一定范围内对P0、Qk、Rk分别进行缩放,缩放后的系统参数即变为kp0P0、kQkQk、｛kRDVLRDVL,kRGPSRGPS｝,从而实现调参。最后,通过回放实航采集的传感器数据及调用惯导内置组合导航算法进行离线仿真,复现AUV的初始对准、水面GPS校准、水下组合导航等全过程,并分析计算SINS/DVL组合导航定位精度。本文使用5km以远的定位误差里程比的CEP50指标(简称CEP50指标)作为优化目标,即有

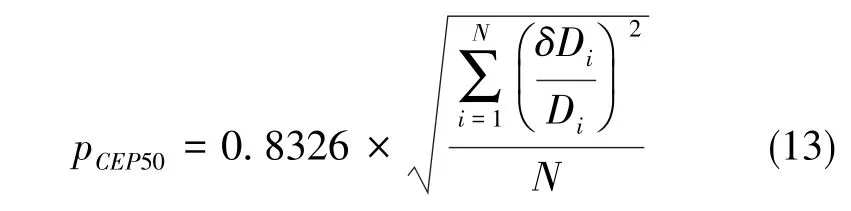
式(13)中,N为测量点数,δDi、Di分别为第i个测量点的定位误差和航程,为第i个测量点的定位误差里程比。

因本文中未使用定位定姿的高精度参考基准,所涉及的定位误差均指惯导经纬度与GPS位置之间的相对误差值。为了保证所计算定位精度的准确性,本文使用CEP50这一统计指标来降低因GPS单次定位跳变对定位精度造成的影响。

这里选取分别对应系统参数P0、Qk、Rk的调节系数kp0、kQk、kRDVL、kRGPS作为设计变量,使用拉丁超立方算法对整个值域空间进行随机抽样计算,建立响应面模型,分析各设计变量与目标量之间的映射关系及贡献灵敏度等,为进一步优化建立起整个空间关系。之后,使用单目标粒子群优化算法,使用响应面模型插值得到的初值以及为各变量分配权重,在限定的｛kp0、kQk、kRDVL、kGPS｝值域空间范围内进行全域目标优化搜索,最终获得使得pCEP50最小的全局最优解,即为该方法整定出的系统参数,其优化流程如图4所示。

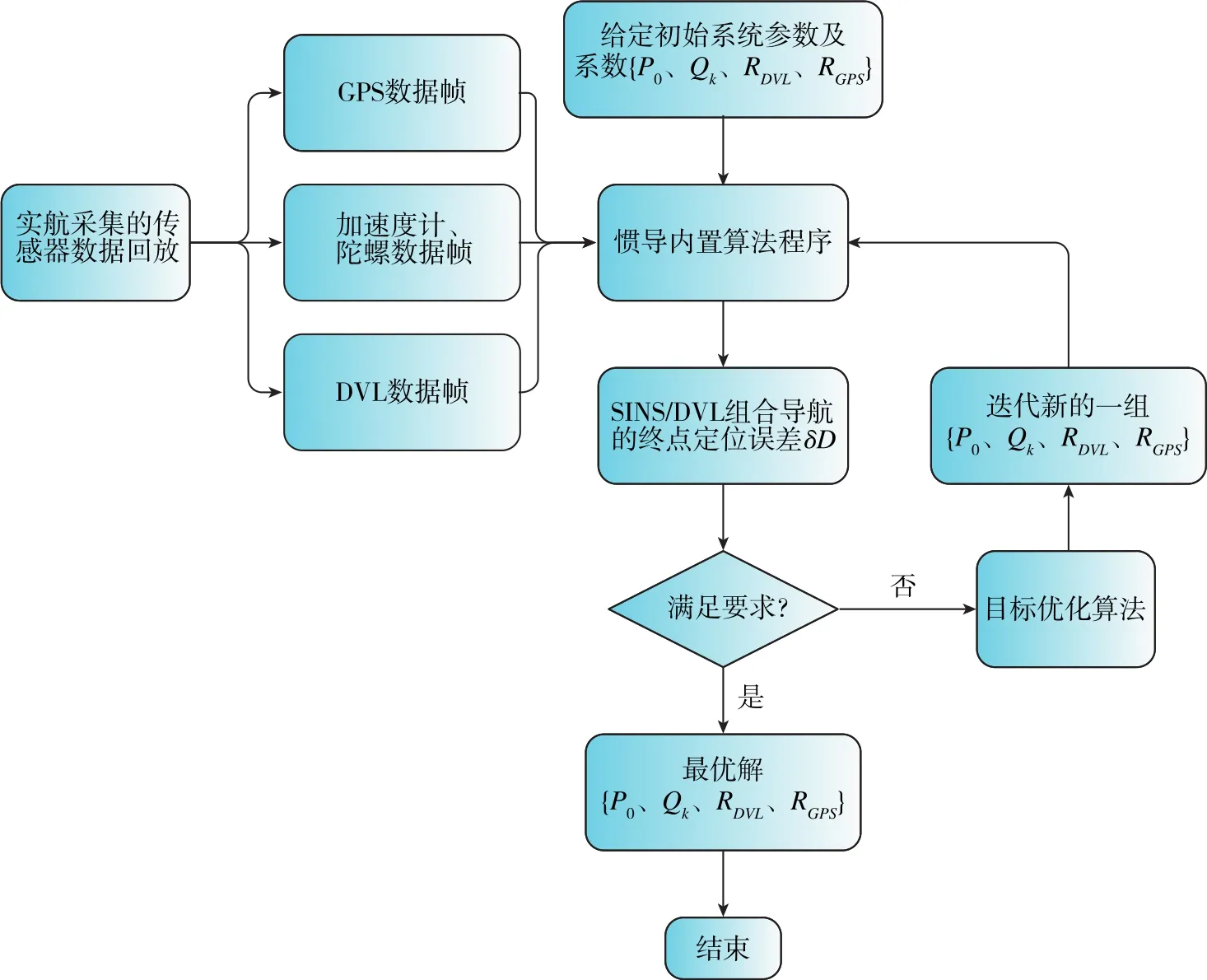
图4 系统调参的目标优化流程图Fig.4 Target optimization flowchart of system parameter adjustment

2 试验验证

2.1 试验方法设计

为了说明本文提出的参数优化方法用于组合导航系统参数调节的有效性,通过下面四个步骤来开展试验验证:1)对PQR参数使用经验值,开展 “初始对准→水面航渡→水下潜航→水面GPS校准→水下潜航”工作方式下的组合导航试验,在整个试验过程中,惯导对加速度计、陀螺、GPS、DVL等传感器数据进行实时存储,同时进行存储的还有下发给惯导的控制指令、惯导状态及导航数据等；2)基于步骤1的惯导内记数据,使用参数优化方法对组合导航系统的参数进行优化；3)使用参数优化方法得出的系统参数开展 “开机对准→水面航渡→水下潜航→出水GPS校准”工作方式下的跑船验证。为了较为准确地评价AUV水下组合导航的精度,本文以AUV潜航5km以远的所有采样点的定位误差里程比的CEP50指标来进行量化。

步骤1中开展的实航试验如图5所示。试验时选择一片开阔水域,AUV的预设航线为A→B→C→D→E→F,整个过程由AUV以自主航行模式进行,AUV将沿预设航线以接近匀速直航的方式跑完所有航路点。当AUV航行至试验起点A后,AUV进行第一次GPS校准,校准完成后沿 AB水下定深自主航行,到达B点后,AUV上浮至水面进行第二次GPS校准,以此类推,分别在 C、D、E、F点进行GPS校准,直到跑完三个直线段后试验结束[24]。其中,虚线代表水面航行,惯导工作在SINS/GPS/DVL组合导航模式；实线代表水下潜航,惯导工作在SINS/DVL组合导航模式。

图5 实航流程图Fig.5 Flowchart of sailing

为验证本文所提出的系统参数调节方法的有效性以及保证试验数据的完整性和便于结果的分析处理,本文在湖北荆门某大型水库搭建了SINS/GPS/DVL组合导航系统,以跑船的方式来进行试验,所使用的器件(或设备)精度为:0.005(°)/h的光纤陀螺、10μg的石英加速度计、0.5%D(D为航程)的DVL和3m定位精度的GPS。

2.2 传统经验值的实航试验

根据本次使用的器件(或设备)的性能参数,组合导航系统的参数设置为

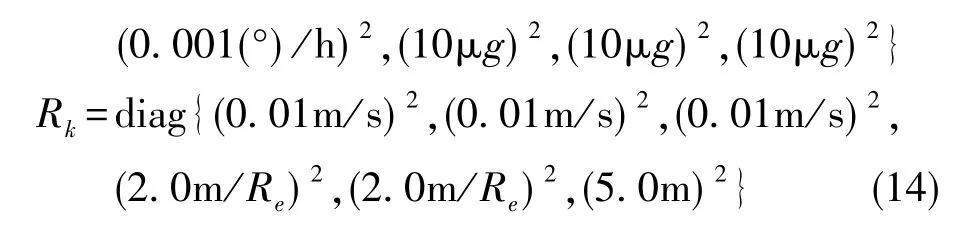
式(14)中,Re为地球半径。

设置组合导航系统参数后,开展 “水下潜航→出水GPS校准→水下潜航”工作方式下的组合导航试验,结果如图6所示。

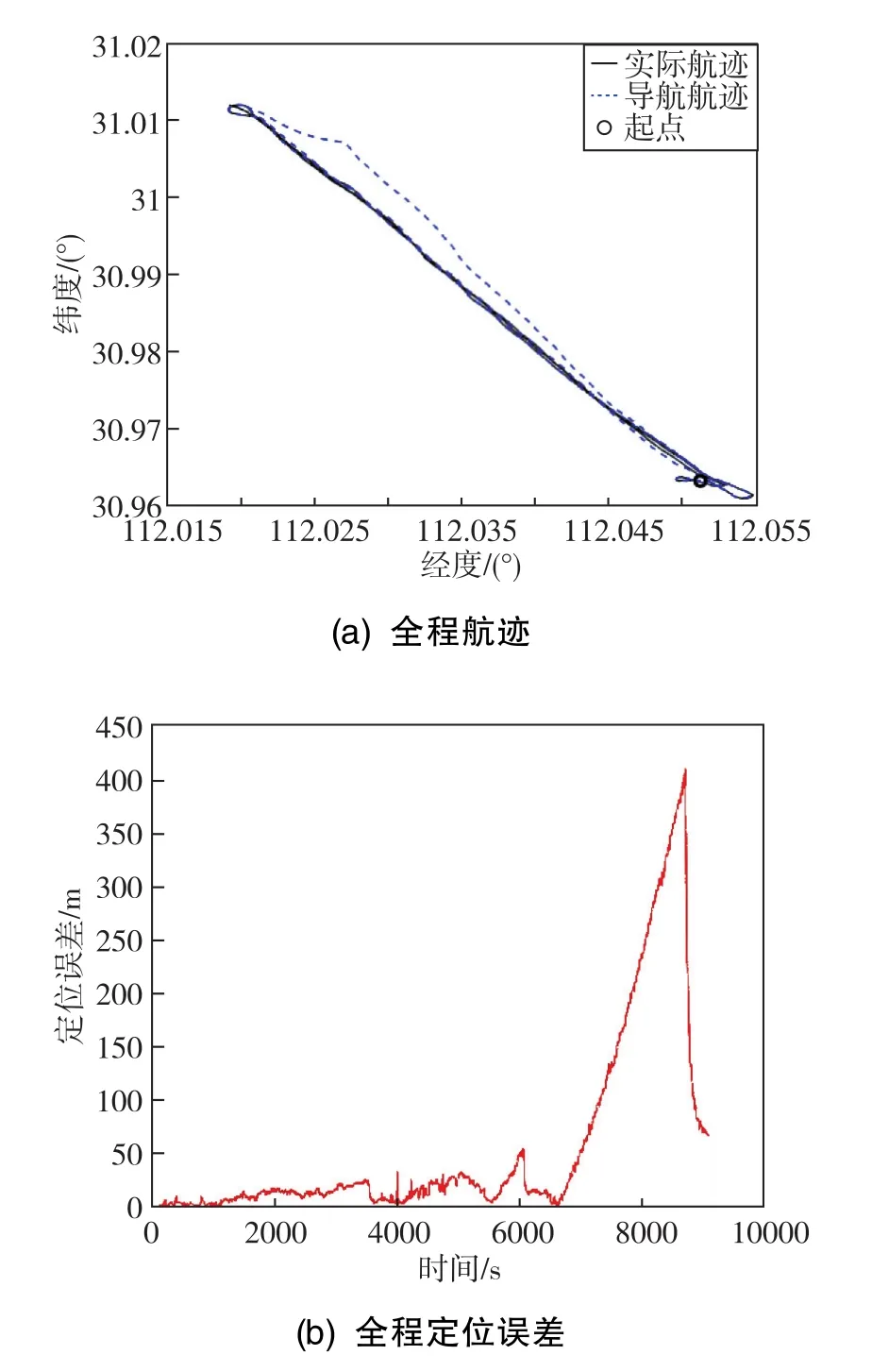
图6 初始参数的实航结果Fig.6 Sailing results of the initial parameters

实航试验中的三个水下潜航段的SINS/DVL组合导航结果如表1所示。

表1 三段SINS/DVL组合导航结果Table 1 Results of the three lines running by SINS/DVL integrated navigation

从未经调参的实航结果来看,第一段水下航程使用0.5%D(D为航程)的DVL组合导航精度为0.34%,表明组合导航系统可以实现较高的对准精度和水下组合导航精度。但在二次水面GPS校准后(限定水面GPS校准时长为1min),系统的收敛速度较为缓慢,无法在限定的时间内完成快速校准。GPS校准结束时刻系统尚未重新收敛,稳定性受到了影响,从而使水下组合导航精度变得越来越差。为了满足使用要求,对系统的PQR参数进行人工调整,使用 ｛0.1P0,960.0Qk,4.6RDVL,0.002RGPS｝作为新的PQR参数,重新开展跑船试验,结果如图7所示。

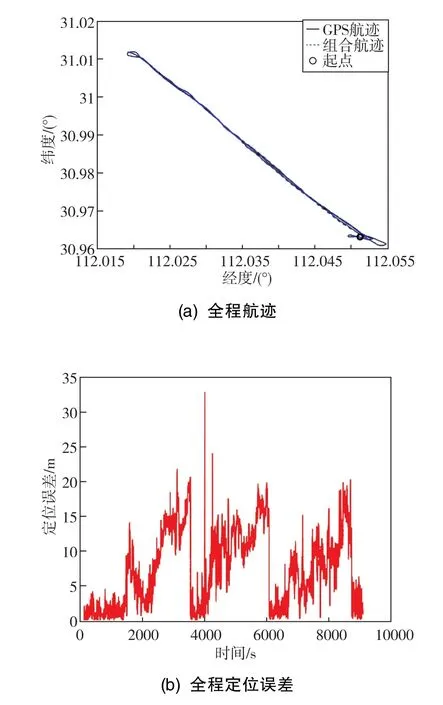
图7 人工调参后的实航结果Fig.7 Sailing results after the manual parameter adjustment

相同条件下(三个水下潜航段),人工调参后的实航试验结果如表2所示。

表2 人工调参后的水下组合导航结果Table 2 Results of underwater integrated navigation after manual parameter adjustment

2.3 基于参数优化方法的系统调参

使用2.2节中实时采集的传感器数据在Optimus优化软件中搭建优化流程,集成调用数据回放和SINS的内置算法程序来离线仿真AUV的初始对准、水面航渡、水下潜航等全过程,以及调用Matlab对SINS/DVL组合导航仿真结果进行CEP50指标计算。为了分析PQR参数中各物理元素对组合导航系统的影响,以2.2节中的PQR经验值作为基准值,使用｛dap,dvp,dpp,ebp,dbp｝、｛webq,wdbq｝、 ｛dvR,dpR｝ 这 9 个变量来对PQR基准值进行缩放,缩放后的系统参数变为

式(15)中,Re为地球半径。

为了同时满足AUV的水面漂浮、甲板系泊等不同工况下的对准需要,同时对GPS+DVL对准、仅GPS对准、仅DVL对准的3种对准方式下的组合导航过程进行离线仿真,以这3组仿真结果中的共9个潜航段的SINS/DVL组合导航精度的CEP50指标的平均值实现最小作为优化目标。之后,对各变量设置足够大的值域范围,选择拉丁超立方算法在整个值域空间内进行600次随机撒种计算,应用响应面模型对计算结果插值出最优解,得到 PQR系数为｛53.89317,57.82437,51.92063,68.92486,44.15826｝、 ｛1810.07749,3544.80884｝、｛14.99721,25.07191｝。

接下来,以响应面模型的插值解为初值,使用单目标粒子流优化算法,以GPS+DVL对准、仅GPS对准、仅DVL对准这3种不同对准方式下的组合导航仿真结果中的9段水下组合导航精度的CEP50指标的平均值作为优化目标,进行单目标优化迭代。迭代过程如图8所示。

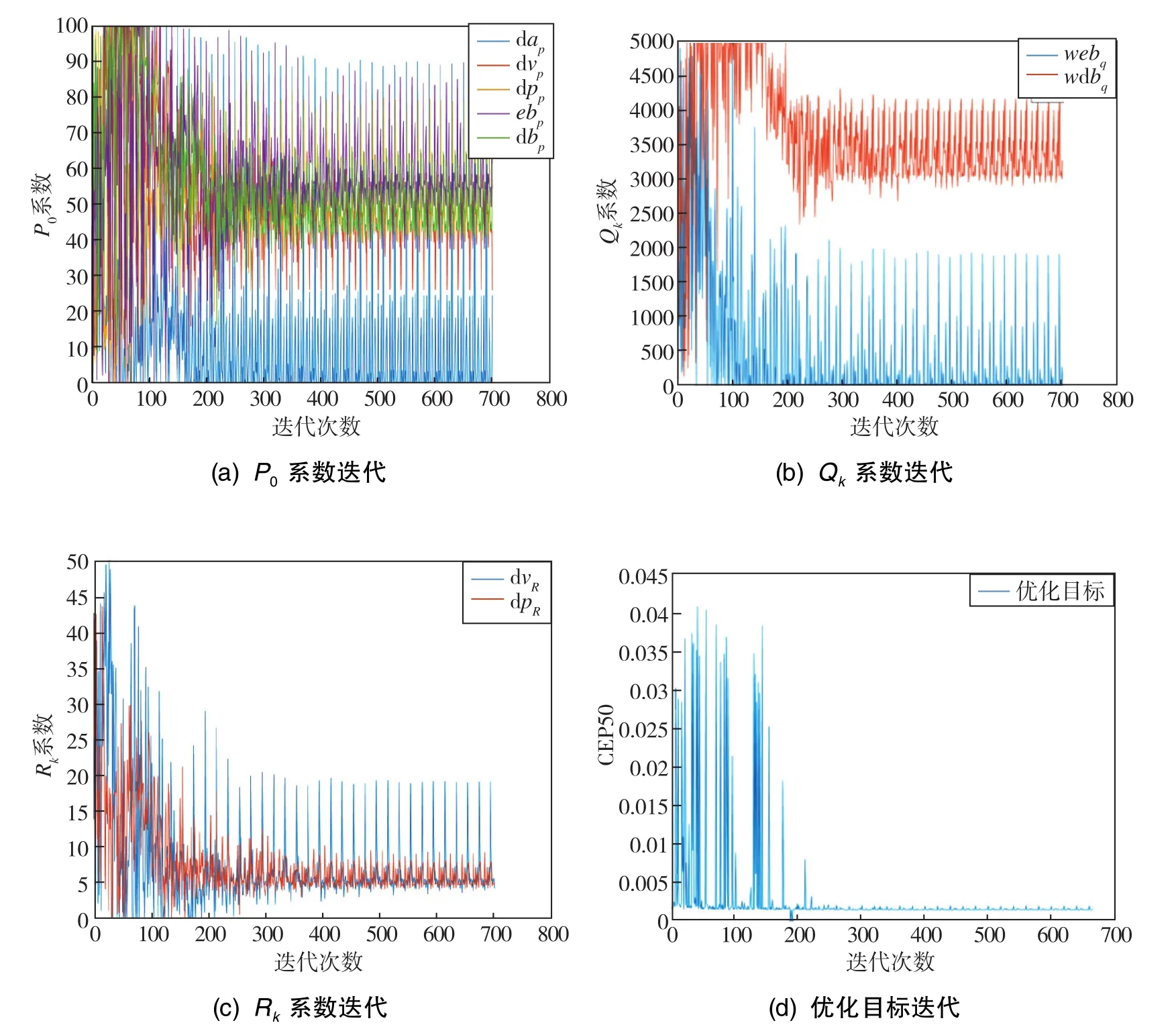
图8 优化迭代过程Fig.8 Iterative process of optimization

经过上述过程,迭代收敛后获得的最优解为｛0.01,32.3058519933,49.9229352822,61.6602577762,51.6745278698｝、｛0.1,4031.04476288｝、｛2.87296322206,3.68002417663｝。以该最优解对应的实际P0、Qk、Rk作为系统参数,分别进行以GPS+DVL对准、仅GPS对准、仅DVL对准的3种不同对准方式下的组合导航过程的离线仿真,结果如图9所示。

图9 最优解的离线仿真结果Fig.9 Off-line simulation results of the optimal solution

使用上述最优解进行离线仿真,结果整理后如表3所示。

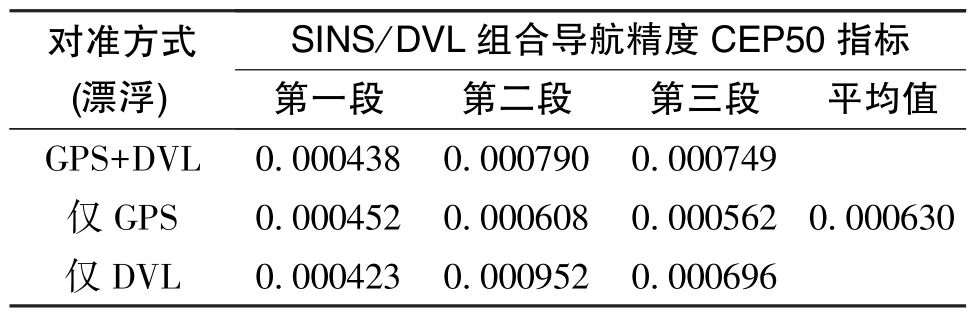
表3 最优解的离线仿真结果统计Table 3 Off-line simulation result statistics of the optimal solution

2.4 调参后的跑船验证和离线仿真对比

对组合导航系统的参数完成优化后,以该最优解对应的PQR实际值作为系统参数,进行包含三个直航段的跑船验证以检验本方法的有效性,结果如图10所示。

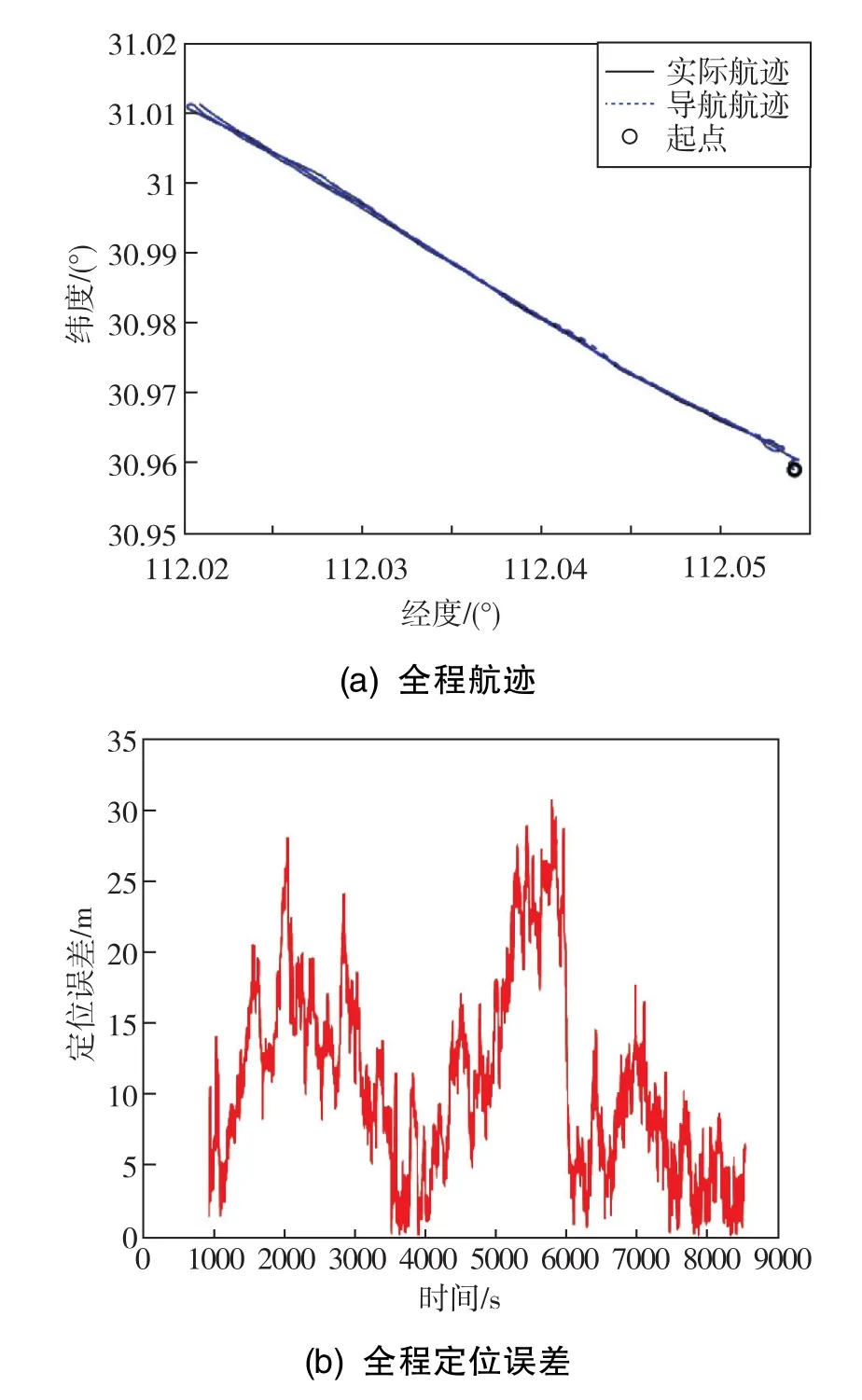
图10 跑船验证结果Fig.10 Results of sailing verification

跑船验证结果整理后如表4所示。

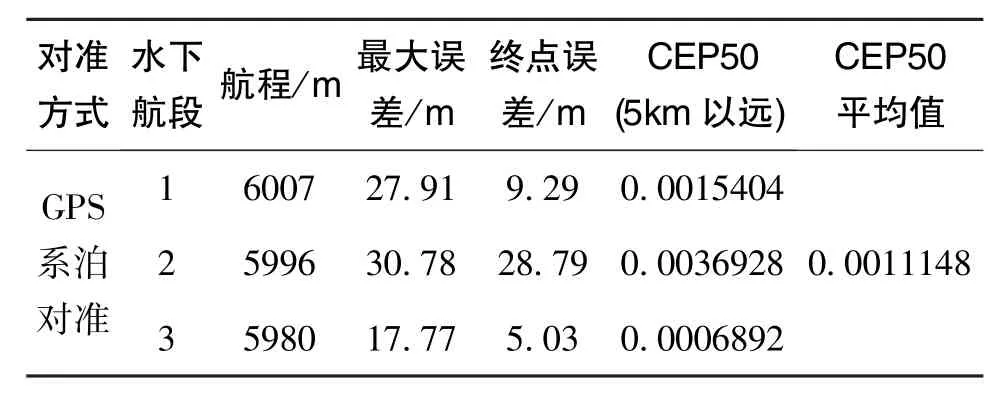
表4 跑船验证结果统计Table 4 Result statistics of sailing verification

为了进一步说明本文提出的PQR调参方法的优越性,开展了4次初始对准+单段6km直线航程的数据采集,分别对使用人工和目标优化方法得出的PQR参数进行离线仿真对比,结果如表5所示。

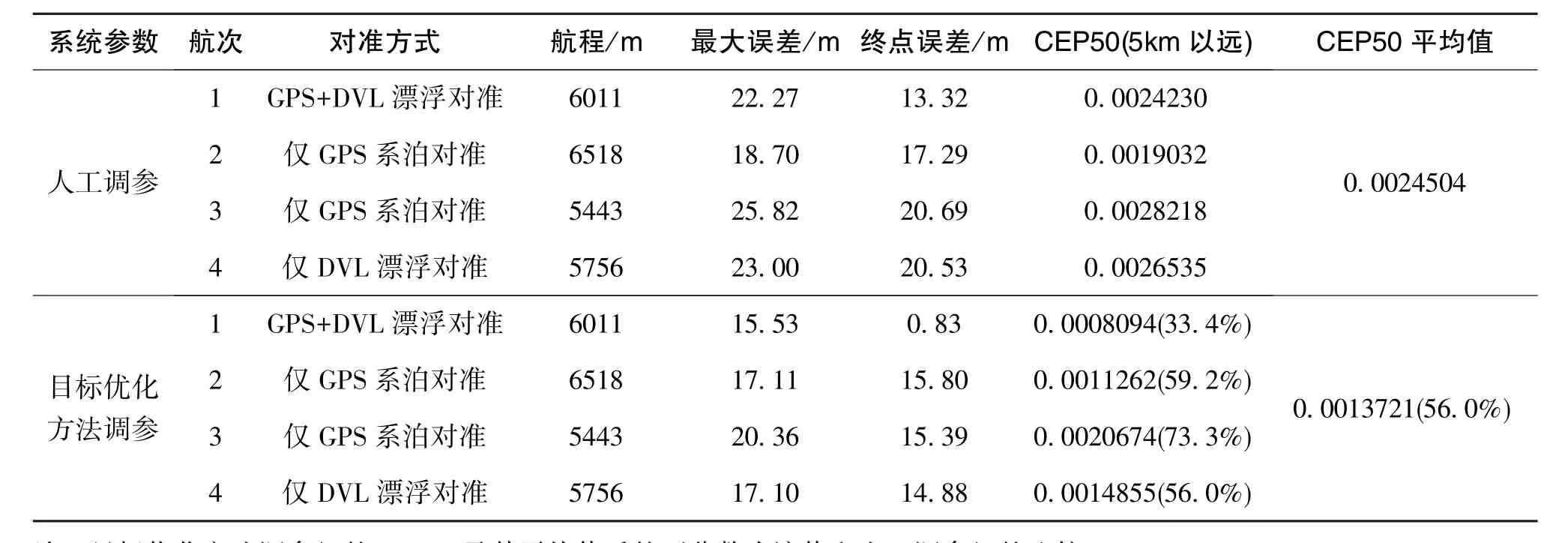
表5 离线仿真对比结果Table 5 Comparison results of off-line simulation

从以上试验结果可以得出如下结论:1)使用陀螺、加速度计、DVL和GPS的性能指标直接设置PQR参数,在跑船验证的第一段中(表1),使用0.5%D(D为航程)的DVL,组合精度为0.34%,表明组合导航系统实现了较高的对准精度和水下组合导航精度。但系统无法在限定1min内完成水面GPS校准,经过GPS校准后的水下定位精度越来越差。2)经过人工调参和目标优化方法调参后,组合导航系统能够在限定1min的时长内完成水面GPS校准,位置误差能够快速校准至1m以内。且水下组合导航性能稳定,不再受到GPS校准的影响。3)使用本文所提出的目标优化方法调参后,水下组合导航的精度得到显著提升,实航验证的CEP50指标由0.252%降低至0.111%,仅为人工方式的44.0%。离线仿真的CEP50指标由0.245%降低至0.137%,仅为人工方式的56.0%。总之,经过参数优化方法调整PQR参数后,SINS/GPS/DVL组合导航系统能够满足工程实际需要。相比传统的人工调参,该方法可大幅提升组合导航系统的定位精度。

3 结论

本文针对AUV组合导航系统的PQR参数调节问题,借鉴多学科优化设计思想,首次提出了基于目标优化方法和传感器实采数据的系统参数整定方法。首先,以跑船实航的方式,使用传统经验值设置PQR参数,开展了模拟AUV“水下潜航-水面GPS校准-水下潜航”工作方式的组合导航试验及传感器数据采集。之后,基于传感器数据回放和组合导航过程的离线仿真,使用参数优化方法对组合导航系统的PQR参数进行了优化求解。最后,使用目标优化方法得到的PQR最优解开展了实航验证和离线仿真对比。试验结果表明,目标优化方法能够应用于AUV组合导航系统的PQR调参,可以保证SINS/GPS/DVL组合导航系统的稳定性和较高的水下组合导航定位精度。使用该方法调参后,经实航验证和离线仿真对比,水下组合导航定位精度的CEP50指标分别降低至人工调参方式的44.0%和56.0%。该方法简单、有效,具有较高的工程应用价值。