“等号”意义文献考察

□ 代婧宇 郜舒竹

等号（=）是一个简洁的、明晰的、人人熟知的数学符号，任何一个等式中都有它的存在，如1=1，1+1=2，y=x+1，等等。按道理，教师和学生都应该非常熟悉等号的意义。然而，部分学生、教师对等号（=）的理解存在片面性，误以为它只具有单方面“运算”的意义而没有等价、相等关系的意义。

一、操作性认识

等式是使用等号表示两个数学表达式呈等价、相等关系的数学陈述，其中，等号当属最重要的符号之一。小学生在一年级学习等号（=）概念时，它被定义为“等于”，如4=4，读作4等于4。到了四、五年级，小学生学习简易方程（含有未知数的等式），教师发现学生总是将未知数单独写在等号的右边去寻求答案。例如，在做这道看图列式题（见图1）时，有学生列出来的方程是这样的：（126-98）÷3=x。

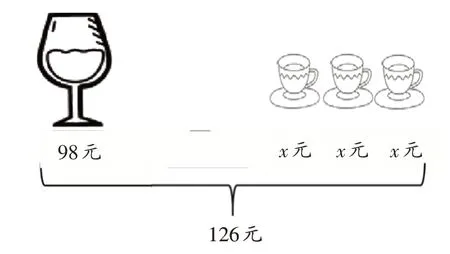
图1 五年级方程的看图列式习题

可以发现，这种方程的形式与“1+1=2”这类等号左边是表达式、右边是答案的算术式高度相似，简单来说，它属于一种“算术式方程”。小学生沿用了之前的经验，书写方程采用特殊的形式：左边有两个或者多个项，右边是结果，中间是一个连接符号——等号。方程也被学生视为算术问题，他们赋予等号操作性的解释，把等号看作一种求得算术结果的标志物。

“将等号看作一种算术运算的操作性符号，而不是代表等价关系的符号”这一观点与麦克尼尔（Nicole M.McNeil）和阿里巴里（Martha W.Alibali）在2005年研究中得出的三到五年级学生对等号的定义的认识是一致的。许多学生将等式中等号前所有的数字相加求答案，看到“=”就联想到“总数”或“写答案”。福克纳（Falkner）等人在研究一至六年级学生对等式“8+4=□+5”的求解后得出结论，学生提供的答案相当于将等号理解为“求结果”，再次表明了学生所持的“等号是操作性符号”的观点。事实上，等号表示的是表达式双方的等价、相等关系。那么，为什么学生会产生“等号是操作性符号”的误解呢？

综合来看，学生产生这一误解的原因主要有两种。第一种，“将等号视为操作性符号”的观点是小学生早期算术训练的产物，他们难以在不同情境下灵活运用等号。第二种，学生甚至不少数学教师对等号的意义了解不够，对等号的概念产生误解，缺乏对等号关系性意义的认识。如果教师意识到方程中的等号表示等价的关系，那么困难便迎刃而解。

从古至今，数学符号发生了一系列的演变才被最终确定，等号并不只有“算术运算结果”这一操作性意义。为此，就需要对历史上等号意义的多样性有所认识。

二、意义多样

20 世纪之前，人们认为等号拥有五种不同的意义。1591 年，弗朗西斯（Francis Vieta）用等号表示算术差（arithmetical difference），作为两个自然数相减之后的差的符号；1638 年，笛卡尔（René Descartes）①勒内·笛卡尔（René Descartes，1596—1650），法国哲学家、数学家、物理学家。他对现代数学的发展做出了重要的贡献，因将几何坐标体系公式化而被认为是解析几何之父。他还是西方现代哲学思想的奠基人之一，是近代唯物论的开拓者，他提出了“普遍怀疑”的主张。他的哲学思想深深影响了之后的几代欧洲人，并为欧洲的“理性主义”哲学奠定了基础。在《几何》中用“=”表示加号或减号，即“±”，等号就相当于现在的“+”或“-”；约翰（Johann Caramuel）使用“=”作为小数的分界线，如“102=857”相当于现在的“102.857”；1706 年，帕里修斯（G. H.Paricius）把“=”“：”和“-”作为通用符号用于分隔解决算术问题过程中出现的数字；迪洛朗（Dulaurens）和赖厄（Reyher）用“=”表示平行线（现在用“‖”），这也造成了当时代数语言的混乱。最终，等号被确定为表示相等关系的符号，在数学中被普遍采用。

进入20 世纪以后，莱特（G.S.Light）在1980 年提出了等号的六种不同的相等意义。第一种是有条件的数字上的相等（conditionally numerically equal），比如 3x-2=7x-6，只有当x=1 时，等式才成立，再如x2+4y2-4x+8y+8=0，此等式出现了两个条件，只有当x=2、y=-1时，等式才成立。第二种是无条件的数字上的相等（unconditionally numerically equal）。第三种是完全相似（exact similar），莱特认为世界上没有完全相似的两种东西。第四种是相同（identical），莱特希望“相同”只具有下面这种语句的含义：昨晚在厨房里跑来跑去的老鼠和今天早上在陷阱里的老鼠一模一样，这区别于“完全相似”。第五种是等价（equivalent），比如：1 元=1 元，在等号的交换性和等价性的基础上，一张旧的1元纸币和一张新的1元纸币是等价的，尽管它们的颜色、外观和序列号都不一样。最后一种，等号还可以表示“是”的意思，有些等式中的“=”可以用符号“→”代替，可以翻译为“成为”，也可以解释为“执行左边运算的结果是右边的表达式”。

1983年，弗赖登塔尔（H.Freudenthal）②弗赖登塔尔（H.Freudenthal，1905—1990），国际上极负盛名的荷兰数学家和数学教育家。弗赖登塔尔指导、推动和亲身参与了荷兰的数学教育改革实践，并对20世纪国际数学课程的改革与发展做出了重大贡献。断言，在数学中，相等符号的使用通常是一个定义问题，例如代数表达式：①x2+2x+1=（x+1）2；②x2+2x+1=0。在第①种情况下，等号意味着所有x的值都是相等的，而在第②种情况下，它意味着等式中的x只有一个值。同年，巴鲁迪（Arthur J.Baroody）和金斯伯格（Herbert P.Ginsburg）提出了多种观点共存的可能性，消除“等号”的操作观是不可能也是不可取的，应该拓宽对相等的看法，使之包含一种关系的意义。保罗（Paul Shoecraft）在1989 年提出“等号”意味着“和……一样（is the same as）”，应该把等式中的“等号”解释为一个关系，用于比较两个实体。例如在8=3+5 中，8 和3+5 是一样的。他还建议教师使用跷跷板、盘式天平、数学天平等帮助学生理解此意义。1998年，在保罗的这一观点的基础上，一些研究人员试图塑造孩子们遇到等号的话语情境，例如采用相同的语言，将等号读作“是和……一样的”。2004年，丽贝卡（Rebecca L.Mann）提出，教师应该帮助学生认识到等号是代表等价和平衡的符号，在教学过程中引入了跷跷板和平衡标尺等帮助学生理解。2006 年，心理学家麦克尼尔（Nicole M.McNeil）得出研究结论：把等号解释成一个信号来执行它之前的运算，学生把“等号”视为“位置指示符”。琼斯（Ian Jones）和普拉特（Dave Pratt）在2012 年认为学生应该使用等号的“关系意义”和“替换意义”这两种不同的意义来解决算术难题。等号左边的内容可以被等号右边的内容替换掉，在方程中也可由数值代替未知数。

乔治（George Boggs）等研究人员还考虑到“=”在数学以外的环境（特别是社交、媒体和广告场景）中的意义。以不同的语言和文化为背景，人们通过概念整合使用“等号”。从隐喻的角度来看，如果源域是数学领域，那么可以映射的目标域就包括结果、价值、状态等等。

第一，“‘加’的结果”。通常指两个或多个输入条件结合，共同产生某种结果或后果。比如“1%的灵感+99%的汗水=成功”，在这种语句中，可以将“等号”的意思推断为收益、结果或原因。其中，加数被映射为活动，加法或加号（+）被映射为连接词“和”等，等号（=）就被映射为合并两个或多个活动的结果，而不是加法计算，等式的右边给出的不是加法的“和”，而是事件的结果和后果。

第二，“简单的结果”。在这种语句中，不需要使用“+”或其他运算符号就能表示因果关系或逻辑关系，如“少休息=多回报”“工作=赚钱”，其中，可以用箭头“→”代替等号“=”。这种语句中都有一个明确或暗含的因果关系来表达实体间的关系，实体的情况、现象等分布在等号的左右两边。另外，这种语句也隐喻了等号的运算意义，问题在等号左边，答案和结果在等号右边。

第三，“定义和描述形式”。比如“No=不可以”，等号表示等价。虽然语种不同，但英文中“No”表达的意思和中文里“不可以”的意思是等价的。

第四，“评估、状态和价值形式”。比如“猪=肥胖/贪吃/懒”，等号所传达的相关状态、价值、形式等只是为了表达某物或某事的状态、价值、形式。这些类别和例子说明等号可以与语境匹配出多个适当意义，不同背景中事物之间的相似或不同之处说明了等号意义的细微差别。

综上所述，等号（=）具有多种不同的意义。如何在众多意义中恰当选择，使等号适用于不同情境，值得进一步思考。

三、等价关系

“关系”就是把双方甚至是多方连接、联系起来进行认知的过程，是从事物之间的相互联系中观察和分析各种现象并揭示其属性以及发展规律的一种思维方式。“=”属于基本符号中的关系符号，理解等号的关系性意义与关系思维有关，学生可以通过专注于等式或方程中数字之间的关系来解决数字语句而不是执行所有计算。如何利用“关系”的思维方式理解等号的多样意义以便于人们使用呢？在此，通过总结前人研究，笔者从“关系”的角度理解等号所代表的意义，将其分为两大类：操作性意义和互换性意义。

小学生计算通常采用操作运算形式，等号左边是执行运算，右边是要得到答案的地方；在“‘加’的结果”和“简单的结果”语句中，不管左边拥有几个活动和事件，右边都包含了现实世界的活动及其后果。这是因为使用了数学中的算术运算模板，引用了等号（=）的操作结果意义。学生将等号定义为运算结果可能是通过描述行为过程，根据行为结果来给符号定一个概念。因此，可以将各种情境下等号用来传达结果的意义统称为等号的“操作性意义”。

等号（=）的操作性意义意味着“在这里写下答案”，是作为“做某事”的符号，表达了“答案是……”“找到总数”的意思，可理解为执行出现在等号左侧的操作的“命令”，或者视为从左到右执行计算的信息。学生只需要操作这些数字就能得到答案。小学生普遍采用的操作形式是表达式=数，即a+b=c。这是他们对于等号最基础的理解，具有严格的操作性。他们只会在等号的左边进行操作，严格遵循“a+b=c”这样的形式进行计算。等号的操作性意义多见于算术中，在小学生眼中，他们相对熟悉等号的这个意义。然而，等号还具有非操作性的意义。

等号一般在等式中出现，它维持着等式两边表达式的等价关系。数学之外，“定义和描述形式”“评估、状态和价值形式”等语句都生动地描述了多种不同事物之间的关系，等号连接着的事物双方在一定语义背景下是等价的。比如一张旧的1 元纸币和一张新的1元纸币等价，工作和挣钱等价……不管是数学领域之内还是数学领域之外，本质上都采用了等号的一种特殊用法和意义，在不同事物间建立左边表达（式）等价于右边表达（式）的联系，描述了对象之间在一定程度上的相同性或互换性。这里，将此等号意义统称为等号的“互换性意义”。等号的“互换性意义”说明两个对象间可以互换（对称），一个对象可以和自身互换（自反），对象间还可以进行传递互换。

等价，强调的是一种关系，在数学中表示等号两边的表达式有相同的值，这其中还含有平衡（balance）的观点。等号两边的值相同，不仅指等号两边是相同的数，还包括等号两边看起来很不一样，是不同的组合，但看似不同的组合，数量可能仍然具有同等的价值。比如：2+3=4+1。从感官上看，等号两边的数字是不一样的；从意义上来看，联想到涉身活动，2+3表示的意思可以是一个箱子中原来有2个苹果，后来又放进去了3个苹果，而4+1表示的意思是一个箱子中原来有4个苹果，后来又放进去了1 个苹果，2+3 和4+1 这两个式子所代表的意义也不一样。但是若把两个式子联系起来，从这些不同中寻找相同就会发现，2+3的计算结果是5，4+1的结果也是5，两个式子在数值上相同，等价关系就成立了。

互换，指等号没有左右之分，等号两边的内容彼此可以互相交换。如，2+3=4+1可以写成4+1=2+3，二者意义不变。

等号还能与变量一起用来描述或表达关于数字之间关系的事实。比如：3x+3=4x+2。根据等式的性质可以得出x等于1，当x=1 时，等式中看似不同的两个表达式构成等价关系，使得等号左边表达式的值和等号右边表达式的值一样。学生对于“等号”的等价关系观，是学习方程的基础。理解等价性要求理解等号两边的表达式的值是相同的，学生要能够从不同的两件或多件事实中寻找相同的部分去建立等价关系。

处于掌握等号互换性意义水平的学生，能够在等号的右边进行操作或者不操作，能理解“c=a+b或a=a”的形式，具有灵活的操作性观点。比如说计算21+30，可以知道21=20+1、20+1=1+20、20+30=50、50+1=51，由这几个算式的等号左右两边进行替换得出，21+30=51。在方程中，数值和未知数可相互替换。比如，将i2=-1 理解为替换规则，即在所有方程中i2都可以被-1 替换，反过来也是一样，在所有方程中-1都可以被i2替换。学生在掌握“a+b=c”之后，又进一步习得了“c=d+e”，根据替换原则能够得出“a+b=d+e”的基本等价关系形式。掌握等号的互换性意义是小学高年级学生运用等价关系处理方程和不等式的基础。

事实上，以“关系”的眼光来看，等号的操作性意义同样属于一种关系性意义，它暗示了等号两边的因果关系。如1+1=2，因为有1+1，所以有了2。

总的来说，等号的操作性意义和互换性意义同为等号的关系性意义，前者暗示了等号两边的因果关系，后者突出了等号两边的等价关系。

四、关系思维

因果关系，是前一个事件（即“因”）和后一个事件（即“果”）之间的作用关系，其中后一事件被认为是前一事件的结果。一般来说，一个事件是很多原因综合产生的结果，而且原因都发生在较早时间点，而该事件又可以成为其他事件的原因。等价关系，描述的是两个事件或对象在一定程度上的相同性，它们之间是自反的、对称的、传递的。等号的操作性意义在语句中所暗示的等号前后的因果关系是有先后顺序的，“因”在前，“果”在后。然而，等号的互换性意义所暗示的等号两边的等价关系是不区分先后和左右的。互换性意义比操作性意义更进一步诠释了等号。因此，等号的操作性意义和互换性意义这两个属概念，虽都包含在关系性意义这个种概念之下，但“操作性”和“互换性”呈并列不相容的关系（如图2）。

图2 等号的操作性和互换性的关系

等号的操作性意义和互换性意义在多数情况下是共同应用的（如图3）。

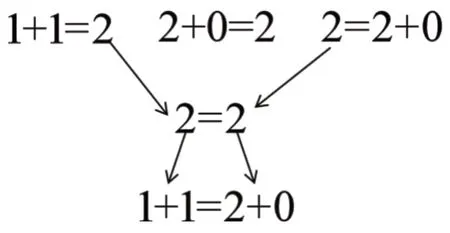
图3 操作性意义和互换性意义共同应用的过程

1+1 的运算结果是2（因为有1+1，所以有 2），2+0的运算结果是2（因为有2+0，所以有2），0+2的运算结果是2（因为有0+2，所以有2），2=2（自反），所以2+0=0+2，经过对称交换，0+2=2+0、0+2=2，所以2=2+0，1+1和2+0的值相同，所以1+1=2+0，显示了等价关系的传递性。

在小学阶段，等号通常以在等式的末尾，后面只有一个数的形式出现。对于只含有数的“a+b=□”形式的式子，例如2+5=7，学生认为等号充当的是“位置指示符”（操作性意义），这种想法是正确的。但是，对于等号两边都含有数的等式和含有未知数的等式（方程）来说，等号充当互换性符号的角色，只看重等号的操作性意义是不够的。等式中，等号两边的表达式的值相等，满足等价关系，等号就不能只是在等式的末尾出现。回到文章开头，根据学生所列出的（126-98）÷3=x这样的“算术式方程”，可以明确学生并没有接受“等号”由操作性到互换性的角色转变，没有灵活运用等号的不同意义，式子中的等号还只是充当运算符号，所列式子当然是不准确的。事实上，把x放在等号末端没有实质性意义。

小学数学教师要想传授等号的等价关系意义，首先要做的就是培养学生关于等号的关系符号的意识。小小的等号不仅仅是一个指向运算结果的操作符号，同时也是表达等价关系的符号，甚至更倾向于表达多方的等价关系。教师在教学过程中应向学生渗透等号的互换性意义，引导学生意识到等号表示的是两边相等，而不只是指导他们计算结果和写答案。

不管是通过“关系”思维对“等号”的多样意义进行分析和归类，还是认识“等号”的关系性意义，都分别进行了同中求异、异中求同的思维过程。同中求异，从相同中看到不同；异中求同，从不同中识别相同。利用数学中与等号相关的知识发展“关系”思维，就可以发展学生异中求同、同中求异的能力。比如用“关系”看待“平行”这个词语。据《新华汉语词典（在线）》所记载，“平行”的基本解释为：平面上两条直线、空间的两个平面或空间的一条直线与一平面之间不相交时的关系。《义务教育数学课程标准（2011 年版）》中的“图形与几何”部分规定了“平行线”的概念：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行。在数学以外的语句中，也有平行思维，指从不同的方向寻求互不干扰、互不冲突的方法来解决问题的思路。物理领域中还有平行宇宙，指从某个宇宙中分离出来，与原宇宙平行存在着的既相似又不同的其他宇宙。虽然“平行”所处的领域、语境、描述对象等都不一样，但是，通过异中求同就可以发现，这些“平行”都有相同的特性：描述事物双方之间互不相交，它们之间的关系是平行的。学生学习平行线段的记忆点不在于两条线一模一样，而在于不管两条线的粗线、大小、长短有多不一样，只要它们永不相交，没有公共点，那就满足“平行”的条件，它与“相交”相对。凡此都体现出关系思维及其在数学理解中的重要性。