依托材料创新，构建新型课堂——《测量地图上的面积》教学实践与反思

□ 严国娟

从数学教学的实际来讲，问题是驱动课堂教学发展的核心。一个好的数学问题不仅可以有效推动课堂教学，还可以为教师开发拓展课提供思路。教师可以以问题为导向，以学具材料的创新应用为抓手，适度融入全科教学的理念，去尝试探寻数学拓展课内容开发的新路径。《测量地图上的面积》就是在这一理念指导下设计的一节六年级拓展课。

【课前思考】

人教版教材中有不规则图形（组合图形）面积计算与估计的相关内容，学生在解决这类问题时，通常采用单纯计算和化繁为简的方法得出结果，缺乏对不规则图形面积的测量经验。基于此，教师针对“不规则图形的面积”这一知识点，以测量某机场面积的现实情境为依托，设计开发了一节拓展课《测量地图上的面积》，立足打破学生对于面积测量的思维定式，鼓励他们创造性地运用学习材料探索求不规则图形面积的方法，促进学生空间观念和创新能力的发展。

《测量地图上的面积》一课的教学目标如下。

1.通过学习和观察，经历运用多种不同的方法测量不规则图形面积的过程，了解多种测量不规则图形面积的方法。

2.在解决问题的过程中提高问题解决能力，积累测量活动的经验。

3.培养数学的应用意识和数学素养，感受生活与数学的联系。

【教学实践】

（一）直接引入，提出问题

师：今天的数学课，我们要一起来研究和测量与面积有关的问题。（揭示课题：测量面积）

教师用PPT呈现图片（如图1）后，继续引导：这是某机场的平面图，我们今天的任务就是求出这个机场的大概面积。先想一想，要解决这个问题，你将面临的困难和挑战可能是什么？

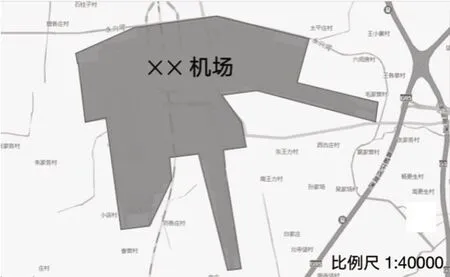
图1

生：它是不规则的，即便知道比例尺，想求不规则的机场的面积也很难。

生：怎么把它变得规则，这是我们要解决的问题。

生：可能不需要把它变得规则，说不定可以有别的方法求它的面积，找到这样的方法就是我们的任务。

师：如果可以借助一些材料或工具帮助你测量，你觉得需要些什么？可以讨论一下。

（设计意图：教学中，教师直接抛出问题，并根据互动了解学生的认知起点。大部分学生都能想到“数方格”或“转化成基本图形计算”这两种他们已经相当熟悉的方法，而借助材料开展测量，探寻解决这一问题的新的可行性路径才是本节课的重难点所在。因此教师设计了学生自主讨论的环节，给学生留足创造性解决问题的空间。）

（二）展开教学，活动探究

1.依据材料，商讨测量方案

教师引导学生讨论交流解决问题需要的材料，并根据学生讨论的结果，提供以下材料（如图2），供学生选择。

图2

师：怎样运用这些材料，对于我们测量面积会有所帮助呢？

生：烧杯是用来测量体积的，我想到了体积等于底面积乘以高，如果把机场的面积当成底面积，把黏土平铺在地图上，再用黏土的体积除以铺黏土的高度，就是机场的面积。

师：你能把面积和体积联系在一起，通过测量体积间接求出面积，是个好主意！那么黄豆可以怎么用？

生：黄豆只能铺在地图上，但是铺好后可以移动变成规则图形再求黄豆的占地面积，就是机场的面积。

生：先算出整块长方形的面积，然后把黄豆间隔均匀地撒在整张地图上，机场上黄豆的颗数除以整个长方形黄豆的颗数就是机场面积除以整个长方形的面积。我们可以用比例的知识解决问题。

（设计意图：在活动设计时，教师尊重学生的差异，给学生提供不同层次的测量材料，让不同水平的学生都能参与测量，体验数学活动的乐趣。运用透明方格纸和剪刀这两种材料进行测量的方法大部分学生都已熟知，并且能够顺利讲解测量步骤和注意事项。这一环节的设计重在引导学生面对新的材料，打破常规思维，发挥创造力，研究新的测量方法。）

2.合作探究，动手实践测量

（1）小组合作，实践测量。

小组讨论协商，选择一种材料进行测量。学生上台展示，介绍自己小组的测量方案与测量中遇到的问题（如图3）。

图3

（2）汇报交流。

生：我们小组直接把方格铺在地图上，不满半格不数，满半格当成1 格，这样结果是111 格，也就是111平方厘米。

师：你们小组用的是数方格的方法。下面我们问问用剪拼法的小组。在剪和拼的过程中你们是否遇到过难题？又是如何解决的？

生：我们小组发现图形剪开后不能完全拼成一个规则图形，所以就将它近似看成了宽7.6厘米、长13.8厘米的长方形，这样面积约是105平方厘米。

师：为什么可以看成长方形来求呢？

生：因为我们把它看成长方形，长方形外面有多的面积，长方形里面也还有空白的地方，可以互补。

师：你们小组选择的材料是黏土和烧杯，你们是怎么用它们来测量面积的？

生：我们先测量了全部黏土的体积，是120 立方厘米，然后把黏土铺在地图中机场的位置上，尽量将高度铺均匀，黏土的高度是1.2 厘米，用公式“体积除以高等于底面积”求出地图上机场的面积大约是100平方厘米。

师：我想问问选择用黄豆测量的这组同学，为什么你们把用黄豆铺成的机场形状变成了长方形？

生：为了方便计算，我们把铺成机场形状的黄豆移动成长方形的形状，虽然形状变了，但是颗数没有变，所以面积还是一样的，只要计算长方形的面积就可以了。

师：当黄豆不够铺满“机场”时，把黄豆均匀地撒满整张地图，你能看懂这其中的意思吗？

生：这个和概率有关系，谁的面积大，黄豆撒上去的概率就大。当黄豆均匀地铺在整张地图上，可以数一数整张地图一共有几颗黄豆，再数出“机场”里面有几颗黄豆。根据就可以大概求出机场的面积。

师：你们特别会思考，原来我们还可以利用部分与整体之间的比例关系来测量面积。

（设计意图：这个环节中，学生在提出问题、商量对策的基础上进行操作，通过思考和实践，自主选择适合的级别进行任务挑战。学生在操作活动中深刻理解面积的概念，主动感悟面积与体积、面积与概率之间的联系。）

3.回顾整理，感悟方法

师：同样都是这一机场的面积，为什么大家测量的结果不相同呢？

生：因为无论使用什么材料，在测量过程中都有可能存在误差，导致结果也有可能存在误差。

师：如何才能减小误差呢？

生:数方格的时候应该注意方格纸不能移动，最好能数1格做一下标记，防止遗漏。

生:在剪拼的过程中应该尽量拼得准确，测量和计算也要准确，把多余的和空白的地方互相填补，以减少误差。

生：铺黏土的时候要注意尽量每个地方的高度都一样，不能有的地方高一些有的地方矮一些，这样用体积除以高得到的面积才准确。

生:在撒黄豆的时候要注意它们的间距均匀，这样算出来的比例才会准确。

……

全课小结：今天同学们用不同的材料，探索了测量不规则图形面积的多种方法。原来面积不仅可以通过计算算出来，也可以通过测量量出来。数学在实际生活中无处不在，我们要学会用数学的眼光观察我们的生活。

【教学反思】

（一）紧扣课堂目标，把材料用对

学生对事物好奇心的强弱、探索欲望的高低、注意力集中时间的长短都与学习素材是否具有吸引力有关。因此，教师有必要根据学生身心发展的特点，在学习材料的选择上下功夫。设计拓展课《测量地图上的面积》时，教师紧扣教学目标，通过提供黏土、黄豆等与求面积大小看起来不相关的材料，来激发学生解决问题的兴趣和愿望，为学生创造力的培养搭建平台。

（二）注重学生本位，把材料用透

1.因“材”施教，提供多样材料

学生思维发展的水平是有差异的。因此，教师应相对把握各个层次学生的思维水平，为不同层次的学生提供不同层次的操作材料，以满足每一位学生的认知需求。本节课的测量活动，提供的是具有难易梯度的学习材料，学生既可以选择格子图，用最为基本的数面积的方法解决问题，也可以选择用剪拼的方法、黏土测量的方法，甚至挑战用黄豆测量的方法求机场面积。这样做不仅做到了材尽其用，还能生成各类生本教学资源。

2.小“材”大用，多种挑战方法

除了给学生提供多样的学习材料外，教师还要关注材料使用的有效性。为避免出现学生盲目使用材料的情况，教师有意在学生正式操作活动开展前对不同材料的使用进行指导和交流，再通过具体操作，小组合作，分类实施，共同完成面积测量的任务。学生测量方法多种多样，既有数一数、量一量，也有剪一剪、拼一拼、算一算等。这样的过程，在提升学生思维能力的同时，也促进了学生团队合作经验的积累。

（三）加强沟通联系，把材料用活

1“.数与代数”“图形与几何”的相互沟通

数与形都是数学研究的主要内容。两者互相依存，在一定条件下可以互相转化。比如学生在用黄豆“测量地图上的面积”时，首先需要考虑到图上单位面积内黄豆的数量，计算整个图形黄豆覆盖的数量，再结合比例尺的相关知识，通过计算相对准确地测量出其大概的面积。再比如借助黏土求地图上的图形的面积，需要先沿着地图边缘将黏土铺平展开，然后依据黏土的体积和高度，求出直柱体底面的面积，也就是地图上的图形的面积。无论哪种方式，都是将原来的测量任务转化为另外一种问题形式，这对学生空间想象力和思维创新能力的培养都具有重要意义。

2.“数学”与“其他学科”的横向联系

数学与其他学科之间都存在交叉关联关系。方格纸、剪刀、黏土、烧杯和黄豆，这一系列看似在美术、科学课程中才会用到的材料出现在数学课堂中，成为帮助学生解决挑战性任务的重要工具。这让数学与其他学科之间相互融合的意味更加明显，有助于学生综合能力的提升。

总而言之，教师在确立拓展课主题和材料时，既要遵循儿童的认知规律，又要尽可能把握学生的思维与能力起点。赋予数学材料以丰富的教育功能，实现课堂教学目标的达成，进一步提升学生综合素养与关键能力的培养实效。