GANs与GRBFNN在空间插值中的对比分析

刘 鑫， 韩宇平， 黄会平

(1.华北水利水电大学 水利学院， 河南 郑州 450046； 2.华北水利水电大学 测绘与地理信息学院， 河南 郑州 450046)

目前气象数据主要来自气象站的直接观测，具有局部性与离散性等特点，利用空间插值的方法可以根据已知气象站的数据估计那些没有气象站但知道经度、纬度及高程的位置的特征。空间插值的方法很多，不同的插值方法结果差别可能较大，在实际应用中并不存在一种普适性的插值方法。常用的空间插值方法主要有普通Kriging法(Ordinary Kriging，OK)[1-2]和反向距离加权法(Inverse Distance Weighted，IDW)[3-4]等。OK法在Kriging插值方法中应用最广泛，通过对已知样本加权平均估计平面上的未知点，而加权平均势必要对数据做平滑处理，会削弱变量的自然属性，从而不能较好地表现非线性特征数据的空间分布。IDW法以插值点与样本点间的距离为权重进行加权平均，该方法要求离散点均匀分布。

人工神经网络(Artificial Neural Network，ANN)处理非线性数据的能力较强[5]，且不依赖数据分布和假设，因此ANN模型被广泛应用于空间插值[6]。徐英等[7]利用Bayes最大熵融合Bayes人工神经网络，在农田土壤水分和养分的空间插值中取得了较好结果。但是ANN学习能力不足，在纯数据驱动模式下建立数据之间的映射关系，ANN容易过度拟合[8-9]。此外ANN只是在输入与输出之间建立映射关系，没有对该映射关系进行优劣评价。虽然ANN也得到一定的改进和完善，但是性能的提升却比较有限。近些年深度学习模型的出现为数据插值处理提供了新的思路，如径向基网络[10-11]、长短时记忆循环神经网络[12-13]及生成对抗网络[14-15]等展示了出色的性能，在预报预测及空间插值等领域取得了较好的结果。

本研究搭建深度学习模型生成对抗网络(Generative Adversarial Networks，GANs)，最小二乘生成对抗网络(Least Squares Generative Adversarial Networks，LSGANs)及Gauss径向基神经网络(Gaussian Radial Basis Function Neural Network，GRBFNN)，期望通过博弈及局部逼近提高降水量和平均气温的插值精度。为了验证GANs、LSGANs及GRBFNN模型在空间插值中的优劣，我们选择OK和IDW法作为基准方法，将GANs、LSGANs及GRBFNN的插值结果与基准方法的插值结果进行对比分析，并进行交叉验证。结果表明：IDW法比OK法更适合对空间数据进行插值；LSGANs和GRBFNN的插值精度优于IDW法，有利于拓展空间插值的应用范围，具有很好的应用前景。

1 研究区与数据

本研究以国家气象科学数据网1960—2013年619个气象站点数据的平均值为例进行实验。

数据包括经度、纬度、高程、相对湿度、降水量、平均风速、气压、平均气温及日照时数。数据样本覆盖中国的海河流域、黄河流域、淮河流域及长江流域等多个流域；涵盖31个省级行政区，包括西藏和青海等高海拔地区、新疆和甘肃等干旱半干旱地区，也包括南方的湿润半湿润地区。研究区涵盖不同地形、不同海拔及不同气候等各种复杂条件。

在实际应用中，我们得到的样本数据是多个维度的，且这些数据可能存在有不符合要求，以及不能直接进行分析的数据，需要经过数据清洗才可以满足模型构建的要求。因此，首先根据箱图筛选出异常值(离群点)，将异常值删除后，对全部缺失值进行插补，插补方法使用Lagrange法。其次，样本数据的量纲和数值存在很大差别。为了消除每个维度之间的量纲与数值的影响，模型训练前要进行数据的标准化处理，使得不同的维度具有相同的尺度，从而解决维度之间的可比性。测试时再全部映射回原始值。

2 研究方法

2.1 生成对抗网络(GANs)

自动编码解码器最开始是一种数据的压缩方法，使用神经网络模型作为编码器和解码器，得到了较广泛的应用[16-17]。编码器慢慢演变成了生成对抗网络的生成网络。生成对抗网络与自动编码解码器最大的区别就是多一个判别网络，自动编码解码器是通过对比输入输出矩阵之间的差异计算损失函数，而生成对抗网络则通过判别网络与生成网络的博弈来更新模型参数，这也是生成对抗网络效果要更好的根本原因。判别网络就是一个判别真假的判别器，相当于完成的是一个二分类的任务。因此，判别网络的损失函数是二分类的交叉熵(Binary Cross Entropy，BCE)：

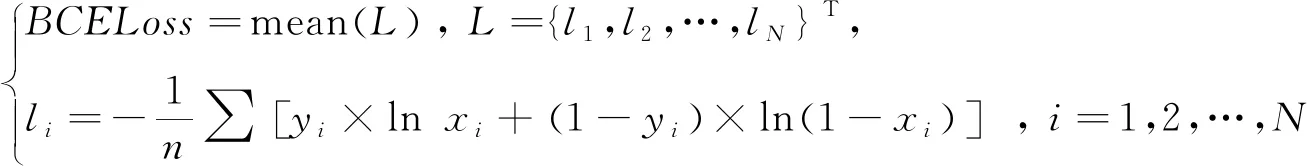
(1)

式中：样本标签y的范围是0～1，yi是目标样本第i个标签；xi是输入矩阵的第i个值；输入输出矩阵都是(N，n)，N是批的大小，n表示特征的维度；函数mean表示求平均值。生成对抗网络的结构见图1。

图1 GANs的缩略图与详细配置

生成对抗网络由两部分组成：生成网络G与判别网络D。输入观测数据时希望D的输出结果是Real(值为1)，输入噪声时希望D的输出结果是Fake(值为0)。这跟原始数据的标签没有关系，不管原始数据包含几个类别，只要是观测数据，输出标签是1，非观测数据的标签是0。生成对抗网络的对抗过程就是生成网络与判别网络的“博弈”过程，掌握观测数据的D不断地对观测数据与生成数据进行判别来更新自身，而G也通过不断寻优，希望产生的生成数据通过D的输出为1，能够“欺骗”D，即G生成的数据能够被判别为真。

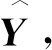
BatchNorm1d是批标准化操作，作用于隐藏层，目的是上一层的输出进行标准化以后再传入下一层。这是因为数据经过这一层网络计算后，数据的分布会发生变化，如果不进行标准化，会增加下一层网络学习的困难，还可能导致梯度消失的问题。Dropout是引入集成学习的思想，将网络中的隐藏层设置为非全连接的，即随机切断某两个神经元之间的连接，旨在训练模型的时候，每层以一定概率P丢弃每个神经元，也就是每次训练的时候有些神经元是没有建立连接的。这样每一次训练之后，训练好的模型都可以看成是一个新的模型，然后训练结束以后，最终模型就可以看成是这些新模型的集成。这样可以增加模型的随机性，本研究取P=0.3。模型中的算法、激活函数及优化器等需要人工设置值的参数，都是根据以往大量的计算、训练及验证经验得出的。

G的隐藏层中先使用Tanh激活函数(式(2))，将数据映射到(-1,1)，输出变成了0均值，后使用ReLU激活函数(见式(3))，简单地将大于0的部分保留，将小于0的部分变成0，因为它是线性的且参数更新过程中不存在梯度消失的问题。

(2)

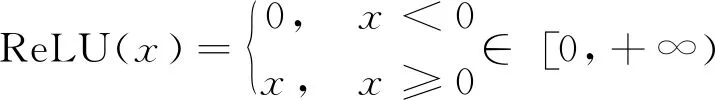
(3)

D中使用LeakyReLU激活函数(见式(4))，这个函数解决了神经饱和问题，它不再是简单的舍弃小于0的部分，而是以一定的斜率留下小于0的部分，可以保证神经元不死。最后输出结果时使用Sigmoid激活函数(见式(5))，将结果映射到(0,1)。

LeakyReLU(x)=max(0,x)+slope×min(0,x)

(4)

(5)

式中：slope在本研究设置为0.2。

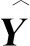
优化函数使用自适应矩估计优化器Adam(Adaptive Moment Estimation)。本研究取Adam的β1,β2为0.9和0.999。为了避免模型收敛到一定程度时会出现震荡现象，使得模型不能较好地持续收敛，本研究采用动态学习率，初始学习率设置为0.000 2，且在训练的过程中设定监视器，实时检测误差的变化。当模型误差持续减小时不对学习率进行更新。当误差反弹时不立即更新学习率，而是等待200次训练后将学习率乘0.9，再等待200次训练之后重新启动监视器，一直到两次更新后的学习率的差小于10-8时关闭监视器。

对于与观测数据非常相似的数据，我们希望D的输出能够趋近于1，对于不相似的数据，我们希望D的输出趋近于0。对于ln函数，在(0,1]上获得的最大值就是0。通过将Noise不断输入D，目的就是将与观测数据不相似的数据全部判别为0或者趋近于0，而希望D(G(x))被判别为1或者趋近于1，使得代价函数V趋近于最小值，使用期望求最值。

V(G,D)=Ex～Preal(x)[lnD(x)]+Ex～PG(x)[ln(1-D(G(x)))]

(6)

(7)

(8)

将数学期望E(x)表示成微积分的形式，可以将V变为式(7)。对于这个积分，要取它的最大值，就是希望对于给定的x，积分里面的项是最大的，即计算出一个最优的D使得积分里面的项最大化。通过对D求导可以得到D*，将D*代回V中。

(9)

(10)

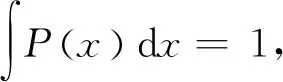
(11)

式(11)中，如果两种分布没有重叠部分，或者重叠部分可以忽略，对于不重叠的部分x的取值，Preal(x)=0或者PG(x)=0，则代价函数恒等于常数，即使两种分布很接近，但是只要它们没有重叠，代价函数就是常数，这会导致梯度为0无法更新。而通过大量实验发现，梯度为0的概率较大，即真实分布与生成分布没有重叠部分的概率较大。除此之外，如果D训练太好，G梯度消失非常严重。如果D训练地不好，G很容易欺骗D，则G可能产生错误的优化方向。如果希望GANs较好收敛，需要D训练地不好也不坏，而这个程度很难把握。因此，GANs的训练非常困难。

2.2 最小二乘生成对抗网络(LSGANs)

最小二乘生成对抗网络(LSGANs)[18-19]，是把交叉熵损失函数换成最小二乘损失函数，期望构建一个更加稳定收敛更快且生成质量更高的模型。GANs的判别网络在输出结果前使用了Sigmoid激活函数。很显然Sigmoid有一个很显著的特点就是将输出结果划分到0或者1，这在分类任务中是很有效的，因为分类任务的目的是将目标的种类进行划分，而目标的种类不是0就是1(二分类)。但是生成对抗网络的目的是生成对抗样本，让D和G进行博弈，二分类没办法衡量这个G到底好不好。而LSGANs把二分类问题变成了求损失的问题，这就更好地为生成模型找准了寻优方向，解决了GANs训练困难及生成样本质量不高的问题，且LSGANs训练过程十分稳定。LSGANs的最小代价如下：

(12)

(13)

式中：a=c=1，b=0。模型仍采用Real(1)和Fake(0)标签，但不做分类而是求损失。

2.3 Gauss径向基神经网络(GRBFNN)

Gauss径向基神经网络(GRBFNN)[20-21]是比较理想的非线性神经网络(见图2)。由于GRBFNN是局部逼近网络，对于输入空间的某个局部区域只有少数几个连接权值影响输出，不仅继承了ANN的优点，还在一定程度上克服了ANN需要调整每一个权值从而导致学习速度慢的缺点。GRBFNN的分类能力和学习速度都优于ANN。此外GRBFNN结构简单、训练简洁、收敛速度快,能在一定程度上克服过拟合和局部极小值问题。

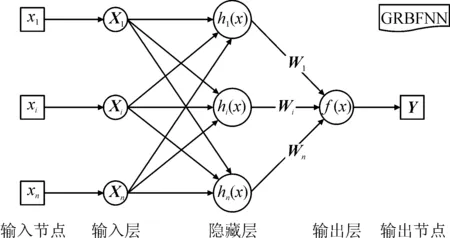
图2 GRBFNN的缩略图

径向基(RBF)是延径向对称取值仅依赖于到中心点距离的实值函数,通常定义为空间任意点x到中心c之间的欧式距离，可以记作dist。然后对dist做一个函数变换，本研究采用Gauss函数，将这个距离函数套入Gauss函数中，得到Gauss径向基函数h(x)，详见下列公式：

dist=‖x-c‖

(14)

φ(dist)=φ(‖x-c‖)

(15)

(16)

(17)

output=w0+f(x)

(18)

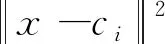
GRBFNN用RBF作为“基”构成隐藏层空间，隐藏层对输入矢量进行变换，将输入数据变换到高维空间内，使得在低维空间内线性不可分问题在高维空间内线性可分，这样就可以将输入矢量不通过权连接,直接映射到隐藏层空间。当RBF的中心点确定以后，这种映射关系也就确定了。而隐藏层到输出层的映射是线性的，即网络输出是线性加权和，此处的权即为网络的可调参数。

见图2，(x1,xi,…,xn)T是输入端，(X1,Xi, …,Xn)T是输入层，(h1(x),hi(x), …,hn(x))T是隐藏层，(W1,Wi, …,Wn)T是隐藏层到输出层的连接权重，f(x)是输出层，最后Y是输出端。输入层到隐藏层的数据变换是非线性的。通过径向基变换之后，将这些结果进行线性加权求和就可以得到GRFBNN的输出，其中激活函数选择为Tanh和ReLU，优化器是Adam，参数设置同上。

OK和IDW法有非常多的公开资料可查，本研究不再叙述，直接利用ARCGIS10.2实现OK和IDW的插值。GANs、LSGANs和GRBFNN深度学习模型使用PyTorch实现。PyTorch是Python的深度学习框架，该框架具有非常强的灵活性及易用性。

2.4 评价标准

本研究评价标准采用均方根误差RMSE(Root Mean Square Error)和Nash效率系数NSE(Nash-Sutcliffe Efficiency Coefficient)。其计算公式为：

(19)

(20)

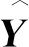
RMSE体现的是估计值与观测值的绝对偏离程度，反应了估计值与观测值的误差。RMSE越小，估计值和观测值之间的误差就越小。NSE系数常用于评估模型的预测能力，代表了插值的吻合度。NSE等于100%表示估计值与观测值完全吻合。估计值越接近真实值，NSE就接近100%。

3 结果与分析

3.1 5种方法插值精度的对比分析

分别应用上述方法建立GANs、LSGANs和GRBFNN深度学习模型，将3个模型的插值结果与基准方法进行对比。表1给出了5种方法对降水量插值的结果。

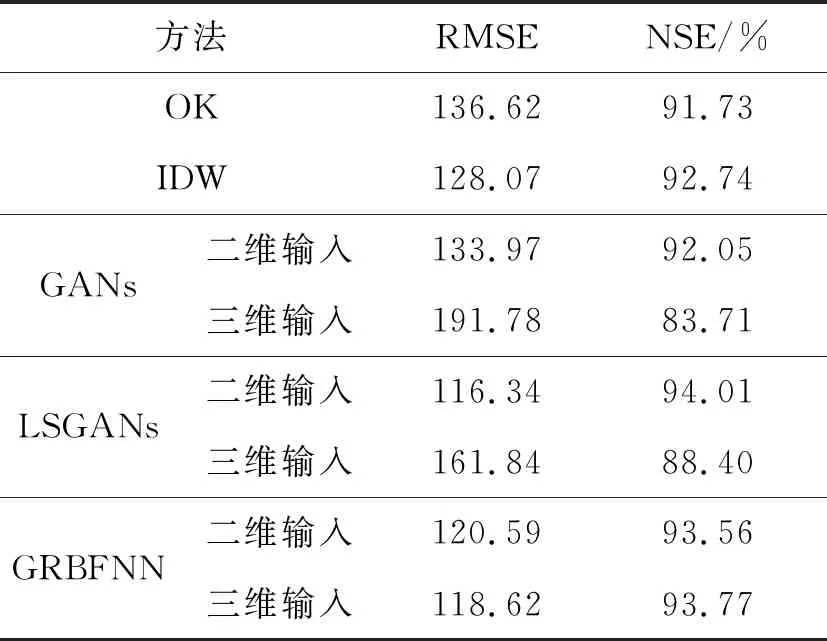
表1 降水量的插值结果对比

因为619个气象站点的高程值存在一定差别，为了探讨高程对于降水量和平均气温插值的影响，应用3个深度学习模型时分别采用两种方式建模，二维输入代表使用经度和纬度建模，三维输入代表使用经度、纬度和高程进行建模。

由表1可知，IDW法的RMSE和NSE都优于OK法。与三维输入相比，使用二维输入，GANs的RMSE减小30.14%，NSE提高8.34%；LSGANs的RMSE减小28.11%，NSE提高5.61%。GANs和LSGANs的二维输入的估值精度明显高于三维输入，可见在降水量的插值中，GANs和LSGANs对于高程比较敏感。与IDW法相比，使用二维输入，LSGANs的RMSE减小9.16%，NSE提高1.27%；GANs的RMSE和NSE虽然优于OK法，但却不如IDW法。对于GRBFNN，二维输入与三维输入的估值精度相差不大，可见在降水量插值中GRBFNN对高程不敏感。使用三维输入的GRBFNN比IDW的RMSE减小7.38%，NSE提高1.03%。5种方法精度最高的是LSGANs。

表2给出了5种方法对平均气温进行插值的结果。结果表明，IDW法的RMSE和NSE都优于OK法。与二维输入相比，使用三维输入，GANs的RMSE减小28.10%，NSE提高5.06%；LSGANs的RMSE减小49.78%，NSE提高8.83%；GRBFNN的RMSE减小47.86%，NSE提高11.5%。GANs，LSGANs及GRBFNN模型使用三维输入的估值精度高于二维输入，可知在平均气温的插值中，3个深度学习模型对高程都比较敏感。与IDW相比，使用三维输入，GANs的RMSE减小18.38%，NSE提高2.71%；LSGANs的RMSE减小39.46%，NSE提高5.16%；GRBFNN的RMSE减小27.57%，NSE提高3.89%。

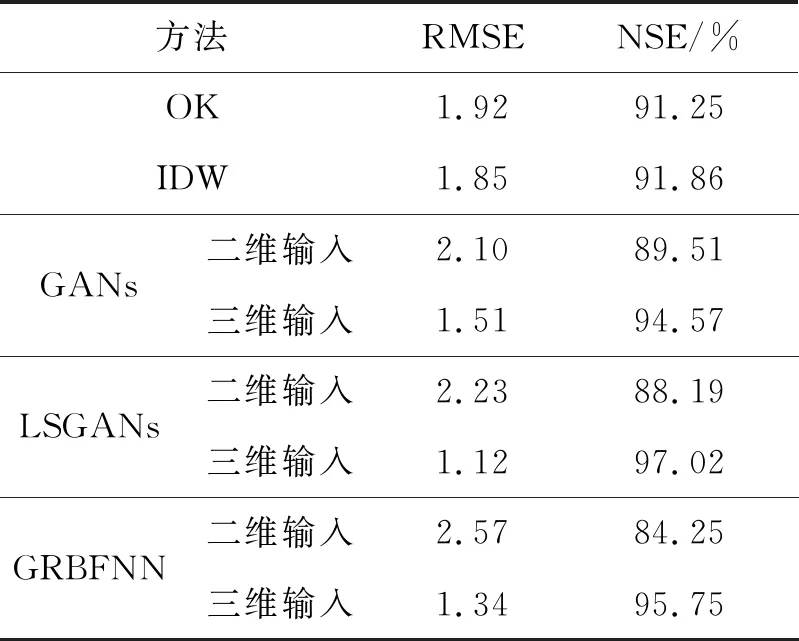
表2 平均气温的插值结果对比

下面对模型的最好结果进行对比。由表1～2可知，在降水量和平均气温的插值中，IDW法的估值精度优于OK法，因此IDW法更适合于空间数据的插值。LSGANs的RMSE和NSE都优于GANs，表明LSGANs在根本上解决GANs模型训练困难及生成样本质量不高的问题。在降水量的插值中，LSGANs的RMSE比GANs的RMSE减小13.16%，而NSE提高1.96%；比GRBFNN的RMSE减小1.92%，而NSE提高0.24%。在平均气温的插值中，LSGANs的RMSE比GANs的RMSE减小25.83%，而NSE提高2.45%；比GRBFNN的RMSE减小16.42%，而NSE提高1.27%。在降水量和平均气温的插值中，3个深度模型的泛化能力排序：LSGANs>GRBFNN>GANs，泛化能力最强的是LSGANs。GRBFNN的效果不如LSGANs，是因为GRBFNN是一个网络训练与测试，只能通过算法减小误差，没有两个网络的博弈，很难捕获数据深层的数量与特征关系。LSGANs通过两个网络的博弈，使得模型能够深度挖掘数据之间的潜在联系，使生成网络学习目标更明确，优化方向更清晰，因此LSGANs的插值精度最高。

3.2 LSGANs的生成对抗过程

本研究从对抗训练过程中，截取600轮的训练数据进行展示，详情见图3。

图3 LSGANs的生成对抗过程

图3的(a)和(b)分别是模型在降水量和平均气温的插值训练时，生成网络G与判别网络D的对抗过程，(c)和(d)分别是模型在降水量和平均气温的插值训练时，估计值与观测值的RMSE变化。从(a)和(b)中可以轻松地看到模型的对抗过程。(a)中黑色曲线G在下降到一定程度时会突然上升，这反映了生成网络G的对抗性质。当G达到一个局部最优值时，G无法进一步欺骗判别网络D，这时G将跳出局部参数空间并调整更新方向，尝试找到更理想的解决方案。而在尝试新方向的优化时，通常会返回较差的生成数据从而导致曲线上升。较差的生成数据在通过D后的输出与Real的误差会变大，导致D的最小二乘损失MSELoss(Mean Square Error Loss)会升高，即D的曲线也会反弹。通过G不断更新自身，产生的生成数据能够骗过D，即生成数据更逼真，此时G的MSELoss将会下降(曲线下降)，产生的生成数据质量较高，再通过D后的输出与Real的误差变小，D的曲线也会下降。随着模型的持续优化，估计值与观测值的RMSE也逐步下降。

由图3(c)也可以获得验证，每次G重新选择优化方向时误差变大，估计值与观测值的RMSE都会反弹一个较大值，之后随着G的更新再持续下降。从RMSE曲线还可以发现，在这600轮训练的最初一段，RMSE曲线处于稳定下降的状态。这是因为图3(a)中，G持续更新自身调整模型参数，G的MSELoss在波动下降，产生的生成数据更逼真。而生成数据质量较高，骗过D的可能性很大，导致D的MSELoss也在波动下降。因此估计值与观测值的RMSE稳定下降。在600轮训练的中间一段，D和G的曲线波动比较剧烈。G调整优化方向之后，多次出现趋于0.25的极小MSELoss，对应D出现趋于0.15的极小MSELoss，估计值与观测值的RMSE也多次出现趋于100的极小RMSE。而在343～600轮训练期间，G的MSELoss仍然在剧烈波动，虽然G的曲线也出现了趋于0.25的极小MSELoss，但是D的MSELoss却稳定在0.3～0.35之间，这是因为经过一定程度的训练，D的判别能力提升，G很难欺骗D，所以对应估计值与观测值的RMSE也没有再出现更小的值。

图3(b)的变化与图3(a)的变化情况类似。唯一的区别就是在第35～205轮训练期间，D和G的MSELoss有一小段波动上升，对应图3(d)中估计值与观测值的RMSE也有一定程度的波动上升。这是因为D的MSELoss波动上升导致G认为目前的优化方向是错误的，因此加快调整自己的优化方向导致G的MSELoss也在波动上升，一直到G找到一个可以让D的MSELoss不再波动上升的方向，而不断的调整优化方向导致估计值与观测值的RMSE也出现增大的现象。

3.3 交叉验证

将训练集与测试集交换作为交叉验证的测试集与训练集。分别应用IDW、LSGANs和GRBFNN对降水量和平均气温进行插值，结果见表3和表4。因为IDW法优于OK法，GANs的效果较差，因此不再进行交叉验证。

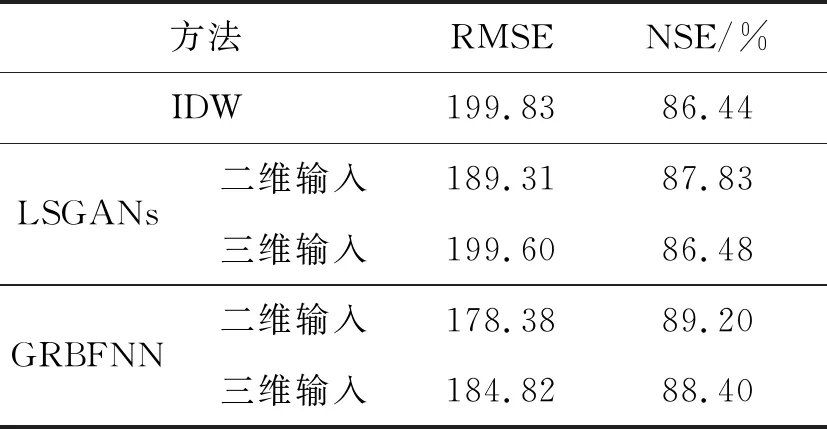
表3 降水量的插值结果对比

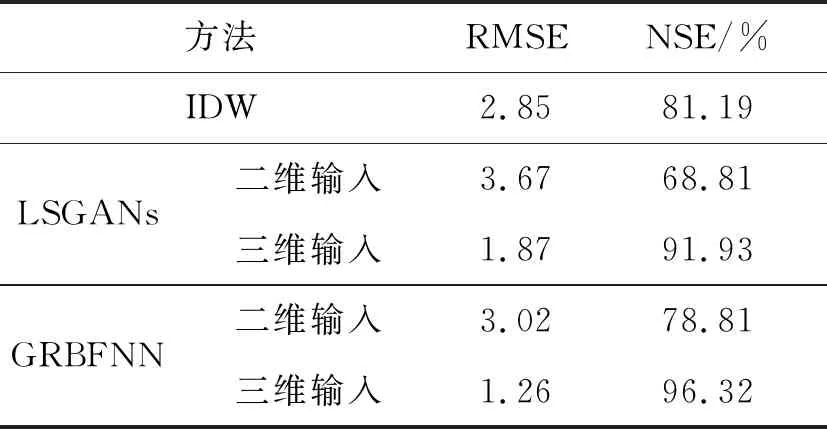
表4 平均气温的插值结果对比

由表3可知，与三维输入相比，使用二维输入，LSGANs的RMSE减小5.16%，NSE提高1.35%；GRBFNN的RMSE减小3.48%，NSE提高0.8%。LSGANs和GRBFNN的二维输入虽然优于三维输入，但是差别不大。这可能是训练样本总量减少导致。与IDW法相比，使用二维输入，LSGANs的RMSE减小5.26%，NSE提高1.39%，GRBFNN的RMSE减小10.73%，NSE提高2.76%。GRBFNN比LSGANs的RMSE减小5.77%，而NSE提高1.37%，GRBFNN的精度要优于LSGANs。

由表4可知，与二维输入相比，使用三维输入，LSGANs的RMSE减小49.05%，NSE提高23.12%；GRBFNN的RMSE减小58.28%，NSE提高17.51%。LSGANs的三维输入的估值精度明显高于二维输入，表明在训练样本总量较少的情况下，模型对于平均气温的插值精度依然对高程很敏感。与IDW法相比，使用三维输入，LSGANs的RMSE减小34.39%，NSE提高10.74%；GRBFNN的RMSE减小55.79%，NSE提高15.13%。GRBFNN比LSGANs的RMSE减小32.62%，而NSE提高4.39%，GRBFNN的精度要优于LSGANs。

综上，对于降水量的插值，建模时更适合使用二维输入；对于平均气温的插值，建模时更适合使用三维输入。当训练样本充足时，LSGANs优于GRBFNN，但是LSGANs的插值精度受到训练样本总量的影响，当训练样本总量较少时，模型的插值精度会降低，插值精度不如GRBFNN。

4 结 论

深度学习侧重从数据驱动的角度来理解过程，在给定复杂空间一部分特征情况下，预测未知特征的能力很强，因此可以提供非线性近似描述数据潜在关系的方法。基于GANs的深度学习模型由生成网络G和判别网络D组成。G尝试从空间数据中挖掘出数据之间潜在的数量与特征关系，并使用学习到的空间知识尽可能准确地生成空间数据，目的是骗过D，而D也不断的优化自身，希望可以判别出观测数据和生成数据。本研究建立了GANs、LSGANs及GRBFNN三个深度学习模型进行空间插值，与基准方法的插值结果进行对比分析，同时进行交叉验证，得出如下结论。

IDW法比OK法更适合对空间数据进行插值。LSGANs进行了改进之后，从根本上解决GANs训练困难及生成数据质量不高的问题。当训练样本较多时，LSGANs在空间插值中表现最好，降水量的插值结果比IDW法的RMSE减小9.16%，NSE提高1.27%；平均气温的插值结果比IDW法的RMSE减小39.46%，NSE提高5.16%。当训练样本数量较少时，GRBFNN的插值精度更高，降水量的插值结果比IDW法的RMSE减小10.73%，NSE提高2.76%；平均气温的插值结果比IDW法的RMSE减小55.79%，NSE提高15.13%。高程对于平均气温的插值精度影响较大，对于降水量的插值精度影响较小。

本研究利用LSGANs和GRBFNN的深度学习模型进行空间插值的想法，期望能给未来有关空间插值的工作带来启发。随着大数据技术和人工智能的快速发展，深度学习模型未来可能在与空间预测有关的各个领域被采用，具有很好的应用前景。