基于网格划分的空间关联区域VOCs浓度预测研究
陆秋琴, 兰 琼, 黄光球
(西安建筑科技大学 管理学院, 陕西 西安 710055)
随着工业化的快速发展,区域性大气污染日益突出,VOCs的大幅度排放引发了诸多环境问题。作为PM2.5和臭氧等大气污染物的重要前体物,VOCs能发生光化学反应并生成有害的二次有机气溶胶等物质[1-2]。部分VOCs易燃易爆,部分VOCs有毒,可以致癌、引起病变,严重危害人体健康[3],所以“十三五”生态环境保护规划将VOCs纳入大气污染防治的重要模块[4]。因此,对VOCs浓度进行预测研究,有助于掌握其发展和变化规律,对制定有效的污染防治对策具有重要意义。不同的研究方法拓展和推动了预测理论的发展,为其他行业的预测研究提供了参考。同时,该预测研究可为环境保护规划提供重要的数据积累,对开展污染控制有着积极的参考意义,也促进了公众参与和居民环保意识的提高。
当前,对VOCs等大气污染物浓度的预测研究主要是在其排放清单的基础上展开的,通过建立基准年的污染物排放清单,来实现其他时段的预测[5]。国内外学者还利用大气排放因子S型曲线预测大气污染物的未来排放趋势[6-7];除此之外,还有基于情景分析法的污染物浓度预测,通过识别关键不确定因素,构建几种可能出现的情景并分析内容[8];优化模型也是污染物浓度预测的常见方法[9-10]。已经提出的大气污染浓度预测模型主要有回归分析、灰色模型[11]、神经网络模型[12]、混沌模型[13]、基于时间序列的模型等[14],以及他们的组合和改进模型。最优定权组合法大气污染物浓度预测是基于多个空气质量模式,以各单项空气质量模式的组合预测误差平方和最小为原则,构建出针对大气污染的预测模型[15]。模糊综合评价方法一般都是结合预测模型来使用。通过模糊聚类分析,将影响环境质量的各因素按主次区分,预测时考虑主要因素[16]。
以上研究还存在一些不足:①由于资金、地理条件等限制,对VOCs并不能做到全方位监测,所获取的数据和信息不太完整;②研究主要集中在数量预测方面,较少通过划分区域精细到每一个网格进行研究;③预测过程中较少考虑气象指标等因素对预测结果的影响。为了解决上述问题,本文提出基于网格划分的空间关联区域VOCs浓度预测方法,以实现区域内VOCs精细化预测研究。
1 网格划分与编号
1.1 区域坐标集合
根据选定区域建立相应的坐标系,建立原则为其中的每一点都能用坐标表示,可以取所选范围比例尺为坐标刻度,获取不同地方的坐标,形成区域坐标集合Rc:
Rc={(x1,y1),(x2,y2),…,(xn,yn)}
(1)
式中:(xi,yi)表示选定区域中的第i个坐标,用二维平面坐标表示,其中i=1,2,…,n;n表示区域坐标点总个数。
1.2 点云网格划分算法与编号
点云网格划分算法是利用点与点之间的距离关系来实现网格划分,基于一点搜索临近点形成线段,根据线段中点临近检索第三点,连接三点形成一个三角网格。对其新边进行中点临近检索,依次形成网格体系,具体步骤如下。
1) 获取区域坐标点集合Rc,初始化一个种子网格。基于点p1=(xm1,ym1)进行临近检索到第二个坐标点p2=(xm2,ym2),连接两点形成线段L(p1,p2),再基于线段L的中点临近检索第三点p3=(xm3,ym3),连接点p3形成第一个三角网格,如图1所示。将网格形成过程中产生的每条边存入集合El,开始时El=Ø。
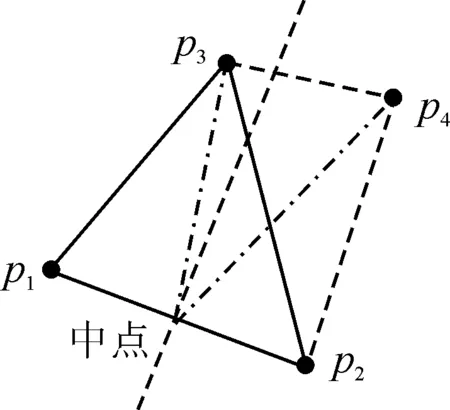
图1 种子网格
El=El∪(p1,p2)∪(p4,p3)∪…∪(pi,pj)
i,j=1,2,…,n
(2)
2) 在种子网格的基础上进行网格扩充,利用中点检索,形成原始网格。从边集合El中获取未进行中点检索的边Lh(h=1,2,…,l;l为边的数量),其端点坐标为pi=(xmi,ymi)、pj=(xmj,ymj),计算其中点坐标Ci,j;从集合Rc检索距离点Ci,j最近且未形成边的点,中点边与新点构造出两条新边,形成一个新的三角网格,并将新产生的边存入集合El中。重复该步骤,直到边集合El中不再提供外边中点检索为止。
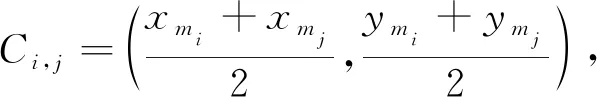
(3)
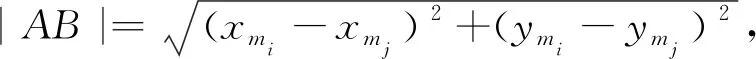
(4)
3) 原始网格扩展,形成新网格。第二步结束形成一个原始网格,检索集合Rc是否存在未形成边的点,如果存在,则寻找新的种子网格重复第一、第二步,直到集合Rc不再有未形成边的点为止,如图2所示,此种情况下所选区域中存在大量的坐标点。在形成网格过程中,如果出现中断现象,只需重复上述第一、第二步形成新的网格即可。
4) 编制网格顺序码,标识网格信息。在初始化种子网格时,将初始化的第一个三角网格编号为001,表示该区域的第一个网格。在网格扩充时,根据网格划分步骤以及检索点算法,对形成的新网格依次编号,最后输出编号后的区域网格以及网格编号信息 [(pi,pj,pk),Num](k=1,2,…,n),如图2所示。其中(pi,pj,pk)表示形成该网格的三个坐标点,即pi=(xmi,ymi)、pj=(xmj,ymj)、pk=(xmk,ymk),Num表示网格编号,其编号值范围为0~999的整数。
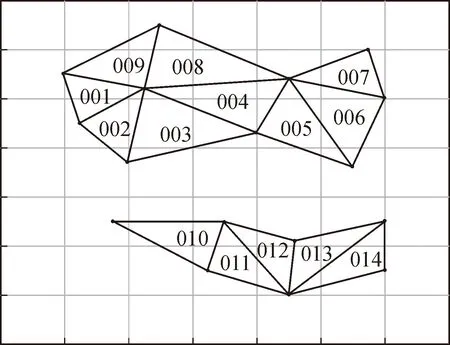
图2 原始网格及网格编号图
1.3 点云网格划分的优点
1) 不规则划分。根据所取点不规则形成大小不一的三角网格。
2) 划分区域选点灵活。根据划分需求可以随意选取点,选点过程能有效避免山川、河流等地理条件的限制。
3) 自动编码。在划分过程中自动编码表示网格,达到网格唯一性和明确性的要求。
4) 点利用率高。在网格划分中采取三点为一的原因是可以将研究区域中所有的点全部划分完,不会遗留未划分的点。
2 空间关联区域数据预估与收集
2.1 空间关联区域数据预估
1) 网格数据预估原理
在实现VOCs精细化监管的过程中,将区域划分成网格,在网格内设置监测点,监测设备在固定时段对网格内VOCs污染物进行监测,能够准确地标识该网格内VOCs污染物的监测浓度值。但由于网格数众多,并不是每一个网格都会设置监测点,为了收集和计算未设置监测点的网格数据,以及预估其污染物发展态势,采取克里金插值法,通过已知网格数据及其与未知网格之间的空间关联性来预估未知网格数据。
2) 克里金插值法预估过程
克里金插值被称为空间最优无偏估计器,它是以变异函数理论和结构分析为基础[17],所选变异函数由数学期望、随机场内特定点的数学期望、方差运算组成。克里金插值法会根据所选的变异函数模型进行模拟,最终对待估点进行预估。
设区域网格坐标点pi处设有监测点,监测值为V(pi),i=1,2,…,n,则未设置监测点p0的估计值可以通过周围n个监测点的监测值V(pi)求得,即
(5)
式中:λi为监测点pi的权重,λi的取值不仅要考虑监测点与预测点之间的距离,而且需结合二者的空间分布关系来确定,样点分布如图3所示。
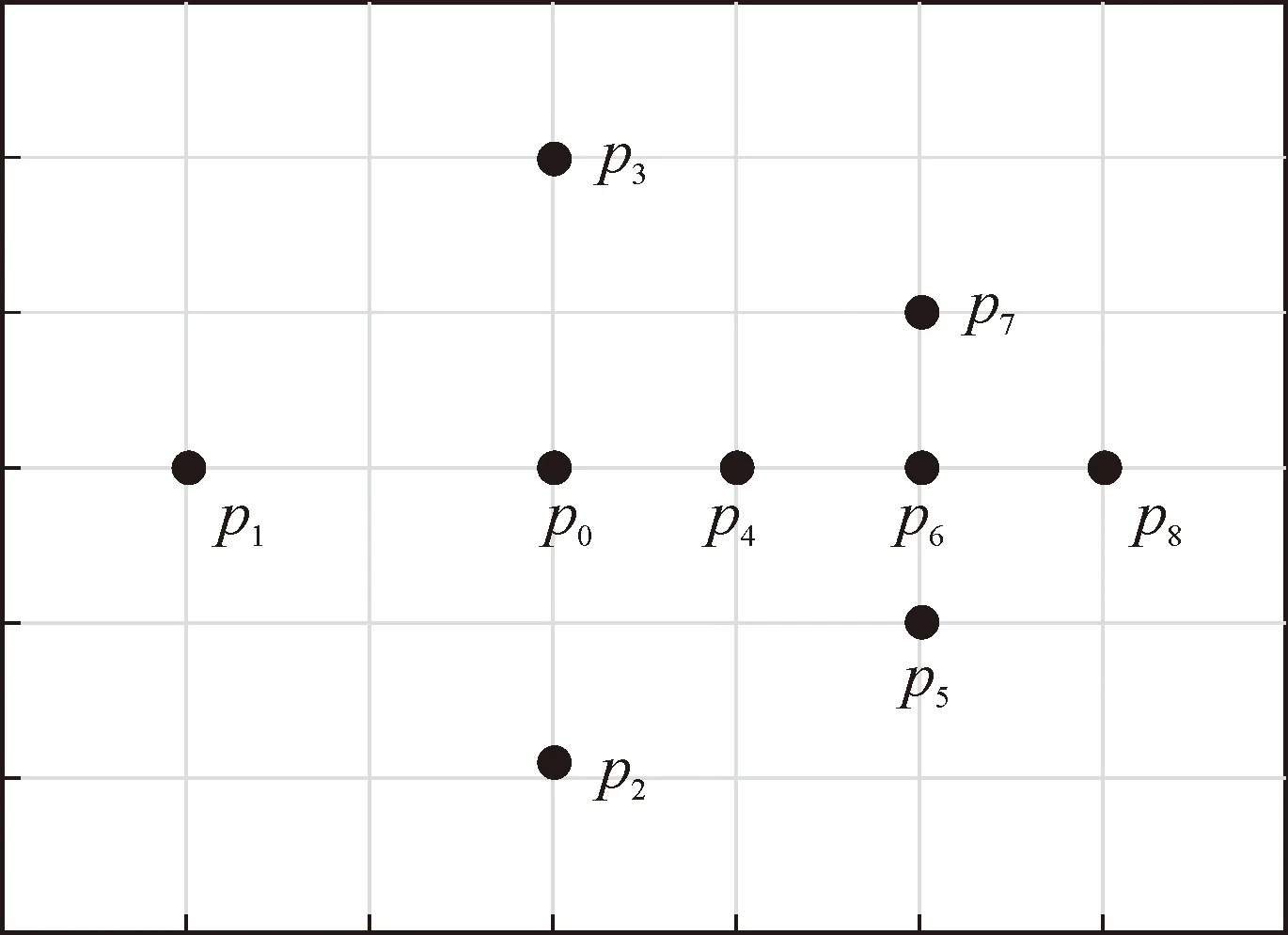
图3 样点分布图
设p0为待估计点,已知其邻域内有p1,p2,…,p8共8个采样点,其位置如图3所示,各点的权重分别是λ1,λ2,…,λ8,由于图中p1、p2、p3、p6到p0的距离相同,并且有p2与p3、p1与p6关于p0对称,则有λ2=λ3,但由于样点p5、p7、p8与p6丛聚在一起,这种丛聚作用降低了样点p6对待估计点p0的影响,p1是一个单独的样点不存在丛聚影响,而且点p6与p0之间存在点p4,由于点p4距离点p0更近,对p6存在屏蔽效应,所以λ1>λ6。
要得到无偏最优估计值,必须满足下面两个条件:
a) 无偏估计,即E=[V(p0)-V*(p0)]=0
b) 估计方差最小,即
Var[V(p0)-V*(p0)]=min
则要求权重λi满足下列方程:
(6)
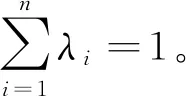
2.2 数据收集及预处理
1) 数据收集
现有的监测设备不仅可以监测到VOCs的浓度(即单位体积排放量),而且可以分析出该区域内VOCs不同组成成分的含量,并将监测数据上传至服务器进行存储,对于设有监测点的网格,通过监测设备获取到VOCs监测值,并按照统一格式处理。已知监测点的监测数据,通过克里金插值法计算未设有监测点网格的VOCs组成成分预估值。将网格监测数据与网格预估数据合并,得到区域网格的VOCs污染物浓度值,如表1所示。

表1 区域网格VOCs污染物浓度值
表1对VOCs主要成分依次划分了编号:苯为1号、甲苯为2号、……、苯乙烯为12号,并结合单元网格顺序码,描述不同网格中不同成分的监测浓度值,如V001(1)表示001号网格中苯的浓度值、V028(12)表示028号网格中苯乙烯的浓度值,依次收集得到区域网格VOCs污染物的浓度值。
2) 数据预处理
数据预处理是对收集到的网格数据进行整理的过程,通过研究区域每个网格的VOCs污染物浓度数据,形成区域VOCs污染物数据集合:
(7)
式中:D表示整个研究区域网格VOCs组成成分浓度集合;vij表示第i网格内第j类污染物的浓度值。
3 基于随机森林算法的VOCs预测模型
3.1 数据集及模型结构
1) VOCs预测模型特征
VOCs预测模型特征可分为两大类型,VOCs污染物和气象指标,具体特征如表2所示。
表2中VOCs污染物特征是指VOCs污染物的烷类、烃类、酯类、醇类、苯系物等具体监测成分;气象指标是指监测当天的气象特征。表2中所有特征形成特征向量集合F。
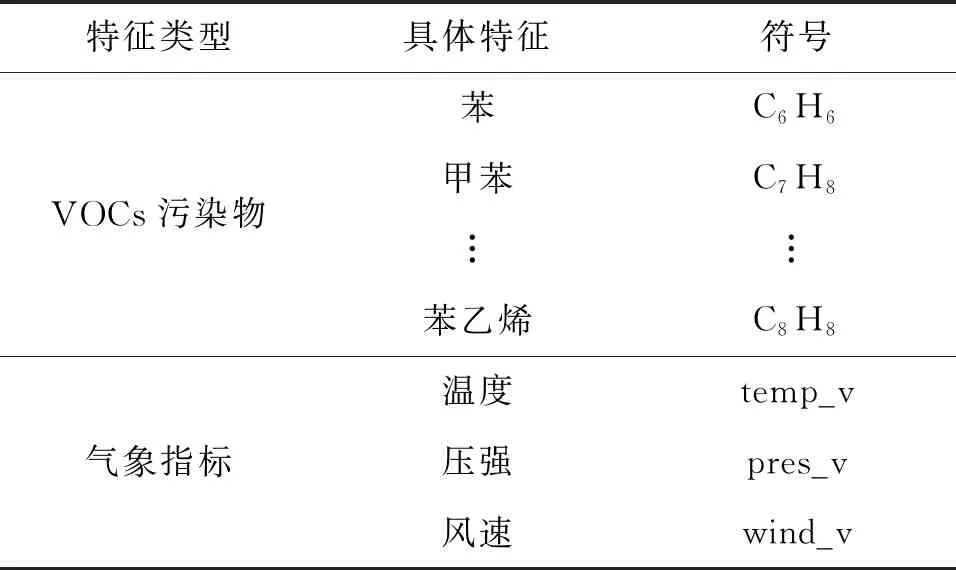
表2 VOCs特征表
2) VOCs预测模型原始训练样本数据集合
基于研究区域VOCs污染物数据特征以及时间维度,形成区域VOCs数据集VD:
(8)
式中:αt1,αt2,…,αti和βt1,βt2,…,βti是时序特征向量,分别表示某一时间段内区域VOCs污染物浓度集合和区域VOCs总浓度序列数据;γ1,γ2,…,γm是非时序特征向量,包含气象指标参数值、VOCs污染物特征。
3) VOCs预测模型构建
在上述数据处理的基础上,运用随机森林算法对研究区域VOCs浓度进行预测建模,建模过程如图4所示。
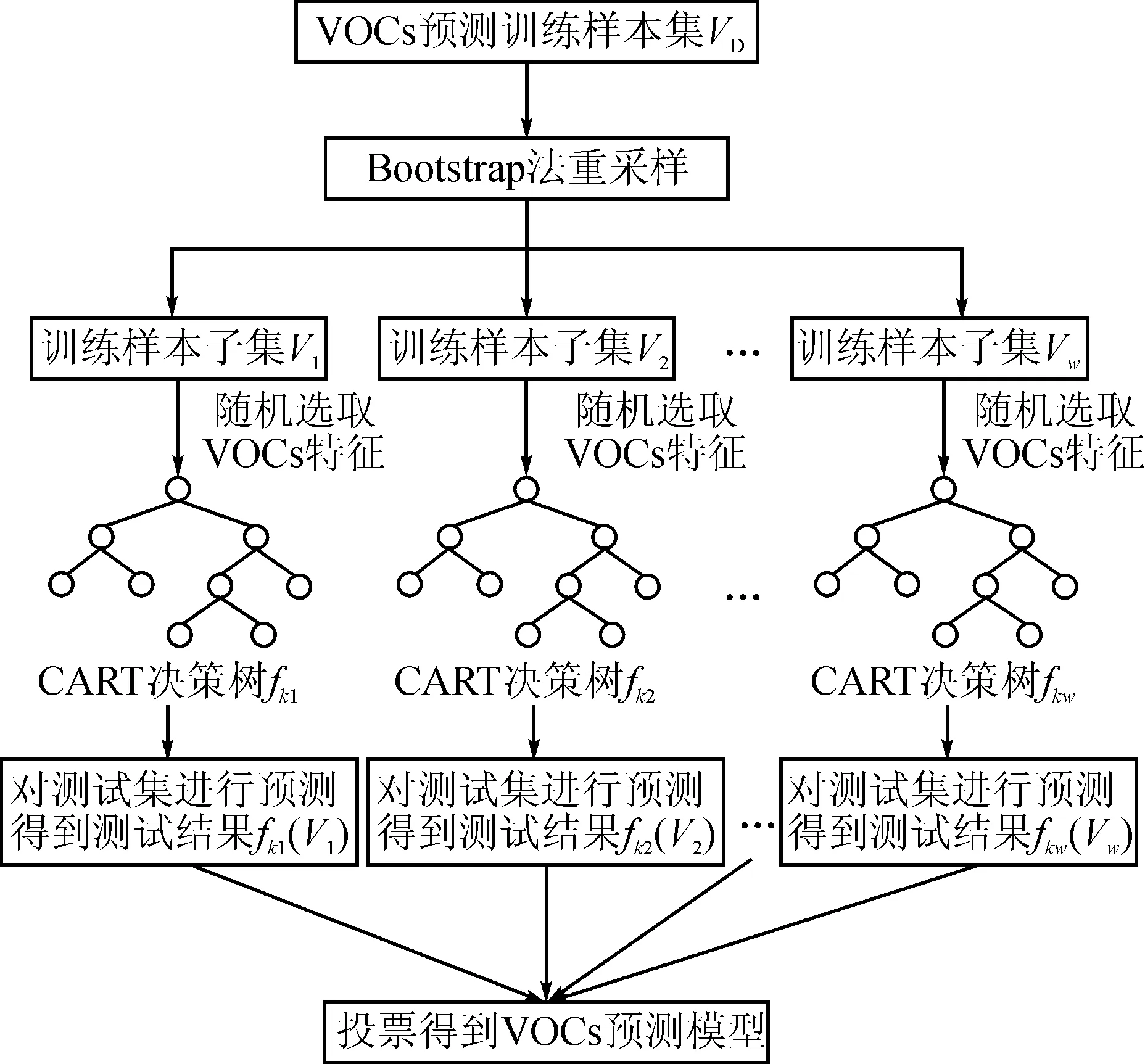
图4 基于随机森林的区域VOCs预测建模过程
首先,利用Bootstrap方法从原始训练样本集VD中随机抽取多个训练样本子集,对每个子集分别进行决策树建模,然后利用测试集对各决策树进行测试,综合多棵决策树测试结果,通过投票得出最终的预测模型。
3.2 训练样本子集的随机选取
原始训练样本子集由两部分构成:一类为VD中区域VOCs总量数据集合βti,将其作为预测模型的输出;另一类为对应的区域网格VOCs污染物平均浓度集合αti和非时序特征数据集合γm,将其作为预测模型输入。
利用Bootstrap方法从VD随机选取w个训练样本子集V1,V2,…,Vw,用于构建w棵分类回归树(CART)。由于训练样本集的选取采用有放回的采样方法,在采样过程中会有36.8%的原始样本不会出现在采集的样本集合中,这些数据称为袋数(out-of-bag,OOB),对CART决策树的误差进行估计。对误差估计取平均,便可得到随机森林的泛化误差估计值,由此可以对VOCs浓度预测模型的精度进行量化度量[18]。
3.3 CART决策树的构建
对每个训练样本子集,采用CART算法生成一棵决策树,共生成w棵决策树。为保证决策树构建的随机性,采用随机子空间思想,从VOCs特征集合F中随机选取m个特征作为随机特征变量,参与决策树节点分裂过程,其中m≤log2(M+1),而M表示特征集合F的集合长度。此外,整个随机森林中决策树的棵数w需根据预测结果来调整。
3.4 VOCs浓度预测结果投票及性能评价
1) VOCs浓度预测结果
当w棵树构建完成后,利用测试集对数据进行仿真。将测试集数据Vk作为输入,得到各决策树模型预测的结果序列{fk1(V1),fk2(V2),…,fkw(Vw)},基于随机森林算法的预测模型最终预测输出的VOCs浓度采用投票方式产生:
k=1,2,…,n
(9)
式中:Fk为组合预测模型;fki为单棵决策树预测模型;I为示性函数;Yk为各决策树预测的结果序列。将预测模型进行线性组合,即可得到区域VOCs浓度预测模型。
2) 性能评价指标
采用通用的模型误差、拟合程度、效率作为度量指标,进行多模型量化评估,如平均相对误差(MRE)和决定系数(R2)。其中R2表示模型输入变量对输出变量的解释程度,也称为拟合优度,取值在0到1之间。MRE越小,R2越接近于1,说明模型准确度越高。
(10)
(11)
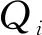
4 案例分析
4.1 数据源
以西安市某区域涉及VOCs排放的企业为研究对象,企业清单来源于北极星网站,时间跨度为2018年6月至2018年12月。VOCs具体浓度数据通过企业年报、地方统计年鉴以及天气后报网站获得。将研究区域划分成不同大小的网格,收集设有监测设备网格的污染物数据,通过克里金插值估计法计算出未设监测设备网格的污染物数据,形成VOCs数据集VD。
4.2 研究区域网格划分及数据收集
1) 网格划分
通过点云网格算法对西安市某区进行网格划分并且对网格进行编号。首先获取该区的坐标点集合,初始化种子网格,然后在种子网格的基础上继续扩充,形成新的网格,以此类推,将整个区域的网格划分完毕,并编制网格顺序码,标识网格信息,结果如图5所示。
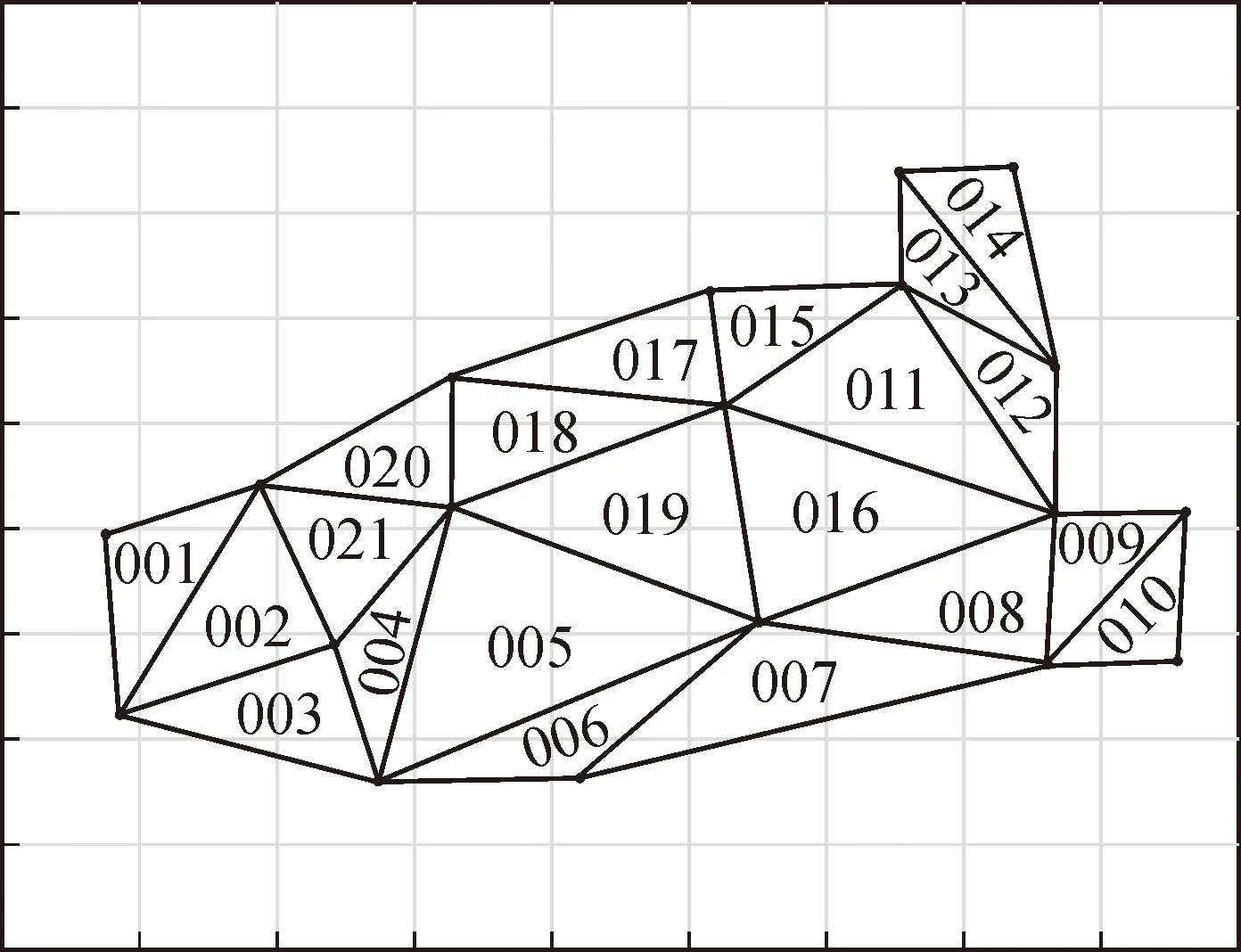
图5 西安市某区网格划分及编号图
2) 数据集
研究区域中有部分网格设有监测点,由监测点获取到网格VOCs监测数据,包括VOCs污染物组分中的甲苯、乙烯、苯乙烯等12种物质,具体监测数值如表3所示。
表3 监测点VOCs污染物浓度值
4.3 空间关联区域数据预估
根据网格坐标点及VOCs污染物浓度值,构建一个40×40的网格,标注范围为1~40,即使网格间距为1。创建矩阵S和Y分别存储坐标值和观测值(即VOCs污染物浓度值)用于预测,根据其预估点和已知数值网格坐标点的空间位置,形成预测值表面,如图6所示。
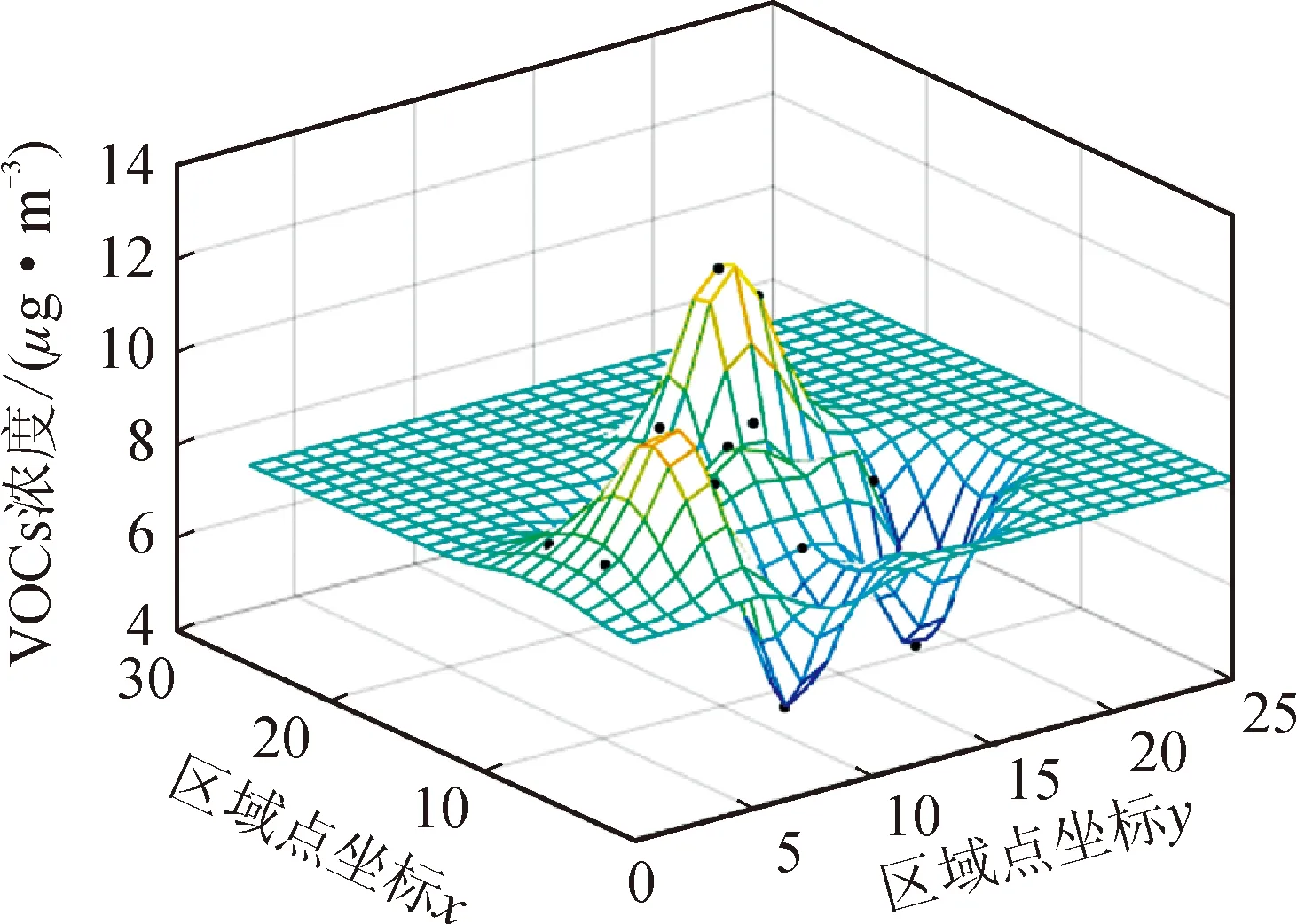
注:黑色点表示原始散点数据
根据图6中预测值表面,结合每个点的拟合误差值,求解出待估点的预估值,拟合误差值如图7所示。
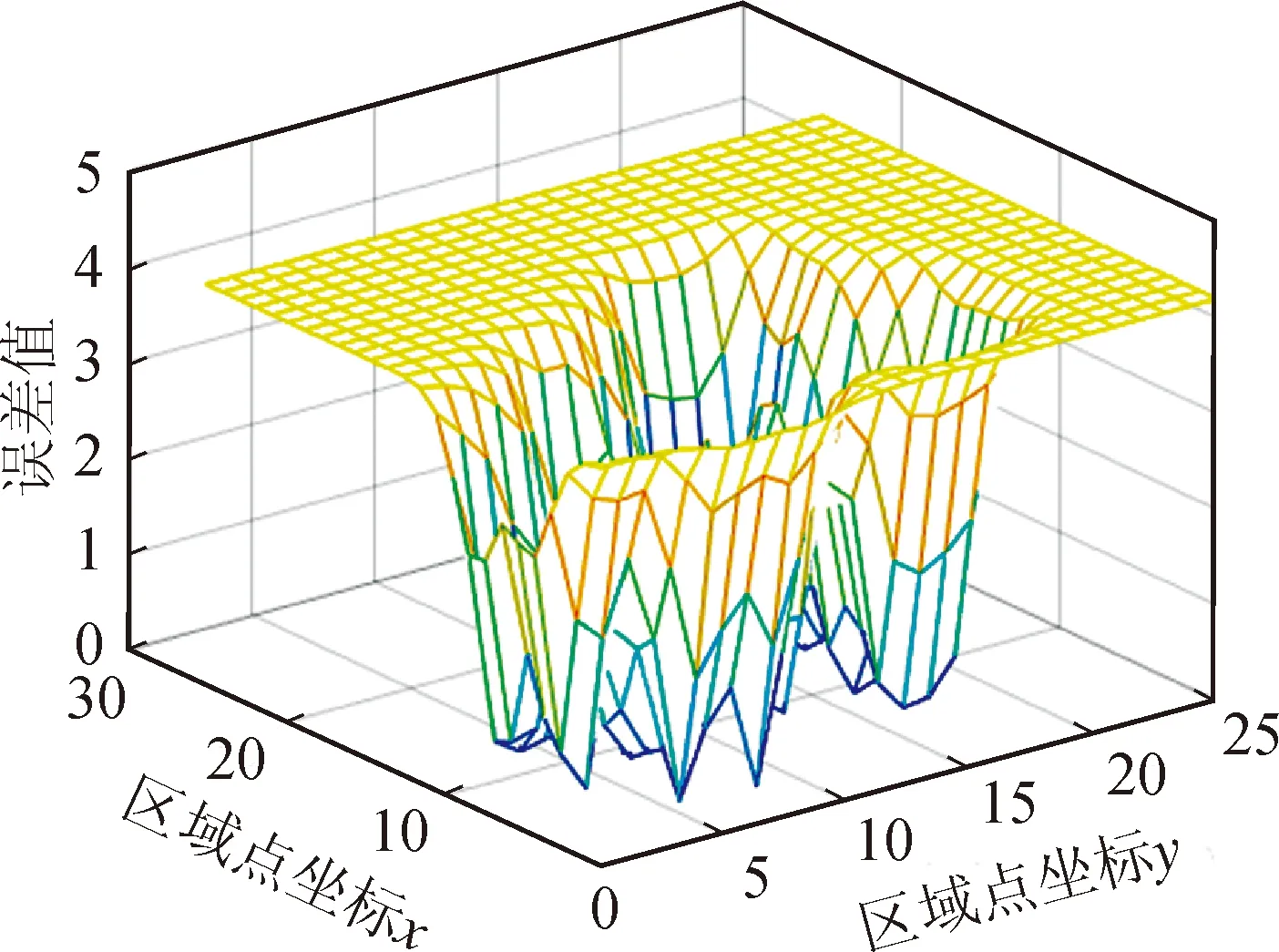
图7 拟合误差值
在λi满足式(6)的条件下,将其相关数值代入式(5)计算出未设有监测点网格的VOCs污染物预估值,具体数值如表4所示。
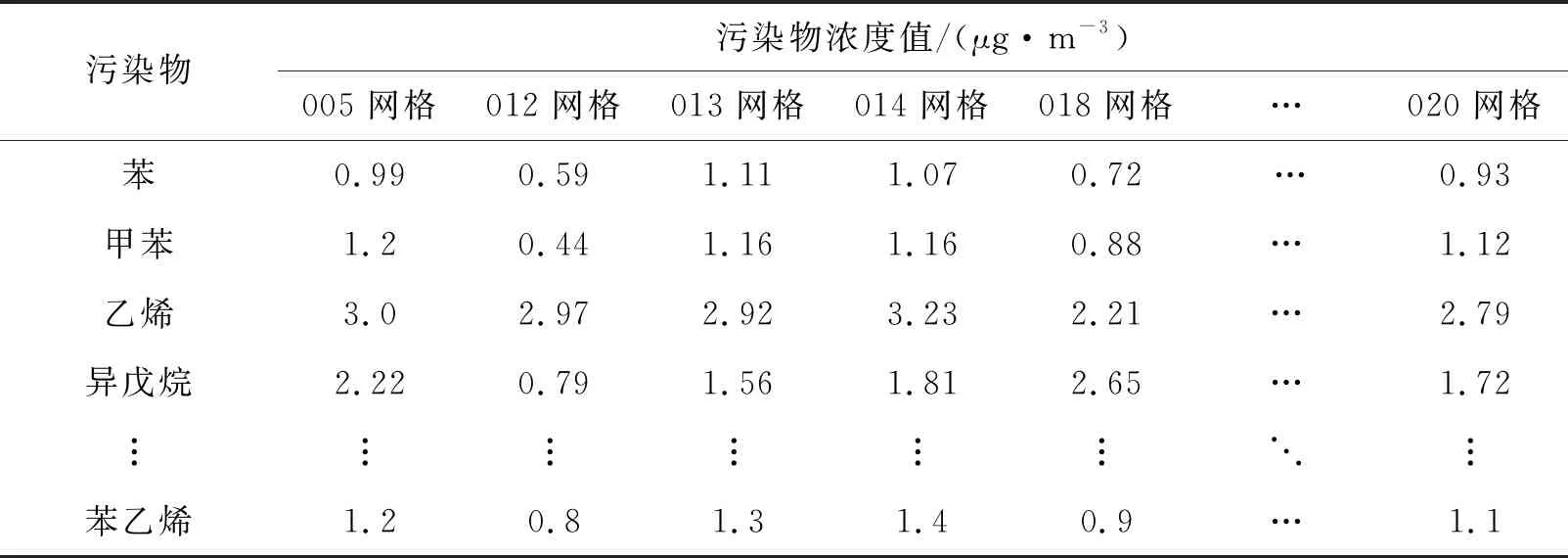
表4 预估点VOCs污染物浓度值
4.4 随机森林模型预测
1) 模型构建及变量相关性分析
通过上述数据收集,获得1 237组VOCs浓度数据,按式(8)处理得到数据集VD形成原始训练样本集,将其划分为训练集和验证集,构建随机森林回归模型预测VOCs污染物浓度。VOCs特征集合F作为变量参与决策树的分裂,模型预测中每个特征所起的作用不同,其相关系数如表5所示。
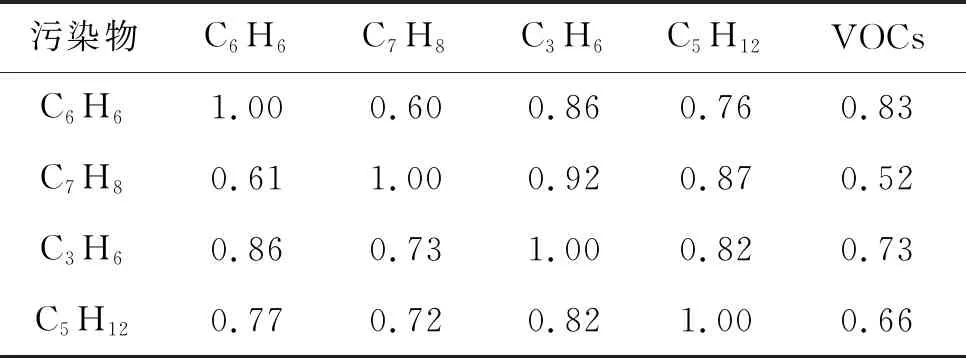
表5 VOCs部分特征相关系数表
根据相关系数表,VOCs与异丁烷以及环戊烷的线性相关性最大,相关系数达到了0.8以上,但是异戊烷与丙烯、甲苯之间的相关系数也达到了0.8以上,即各因素之间存在多重共线性,不满足相互独立条件,不能直接进行线性回归,所以采用随机森林预测。
2) 模型训练、验证和评估
将原始数据集合分为训练集和验证集,由式(10)、(11)分别进行模型的训练和验证,并对模型训练和验证结果进行评估,如表6所示。
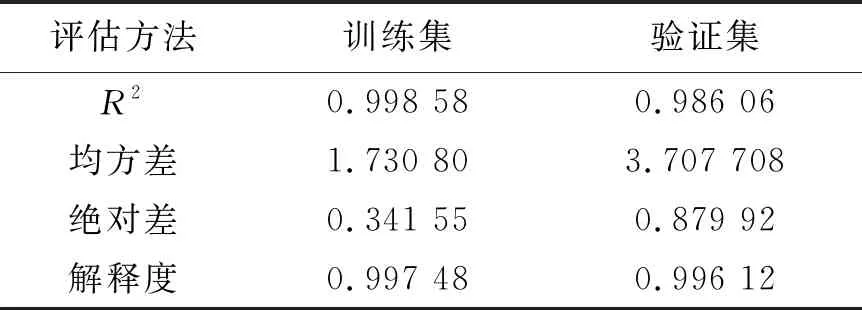
表6 模型评估参数表
表6中训练集和验证集的相关评估参数值相差很小,其决定系数R2以及解释度均达到了98%以上,表明模型在自变量不发生变化的情况下,因变量的变异概率极小。模型训练过程中,各特征参数的重要性如图8所示。
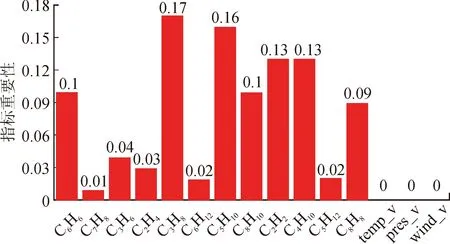
图8 VOCs特征影响系数表
图8表明, VOCs污染物的预测中,烷烃类污染物重要性比较强,相对而言温度及压强作用比较小。
3) VOCs污染物浓度预测
从设有监测点网格中选取19组数据作为预测集输入模型,得到各决策树的预测结果序列,再根据式(9)投票筛选出最优预测结果,预测结果如表7所示。
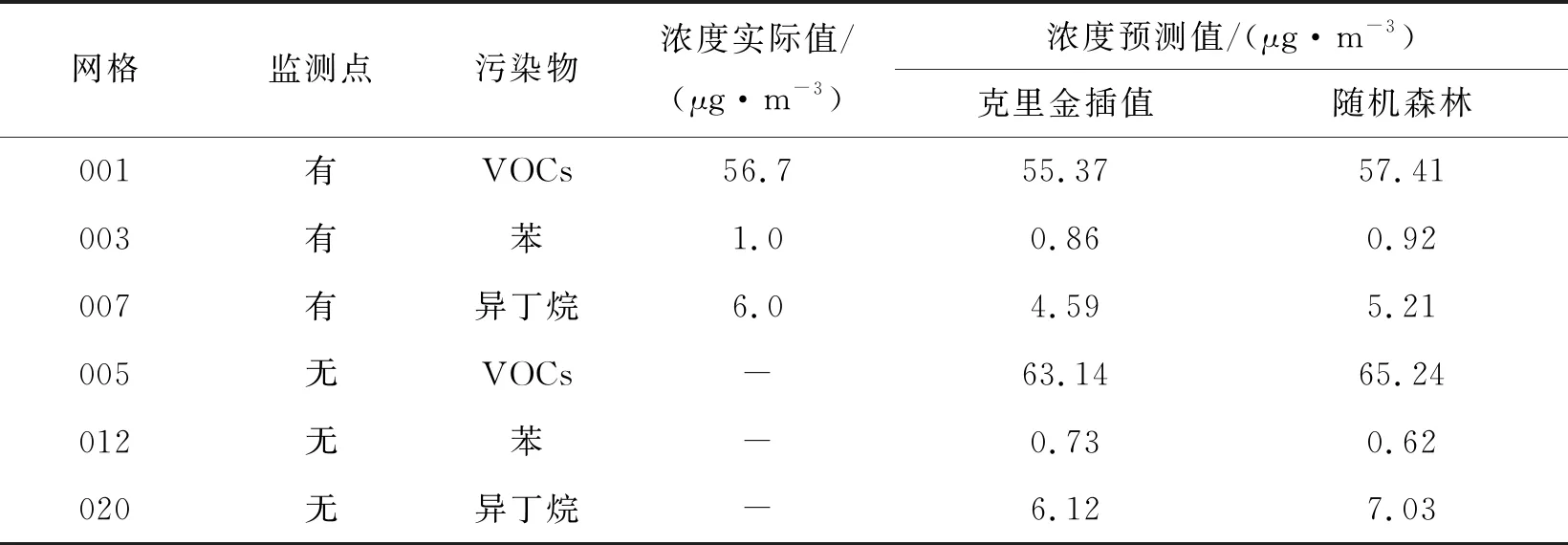
表7 VOCs污染物浓度预测结果
4) 模型比较
本文是基于网格空间特性以及随机森林回归模型实现VOCs污染物浓度预测,现将预测结果与常用的BP神经网络预测结果进行比较,如表8所示。
表8给出了不同网格在两种预测模型下的VOCs污染物预测值,未设置监测点的网格VOCs污染物实际值用克里金插值预测结果代替;分别采用相对误差和平均相对误差对两种模型进行分析。由表8可知,随机森林模型和BP神经网络模型的VOCs总量预测值的平均误差分别是3.15%和13.36%,由此可见,随机森林回归模型误差更小。
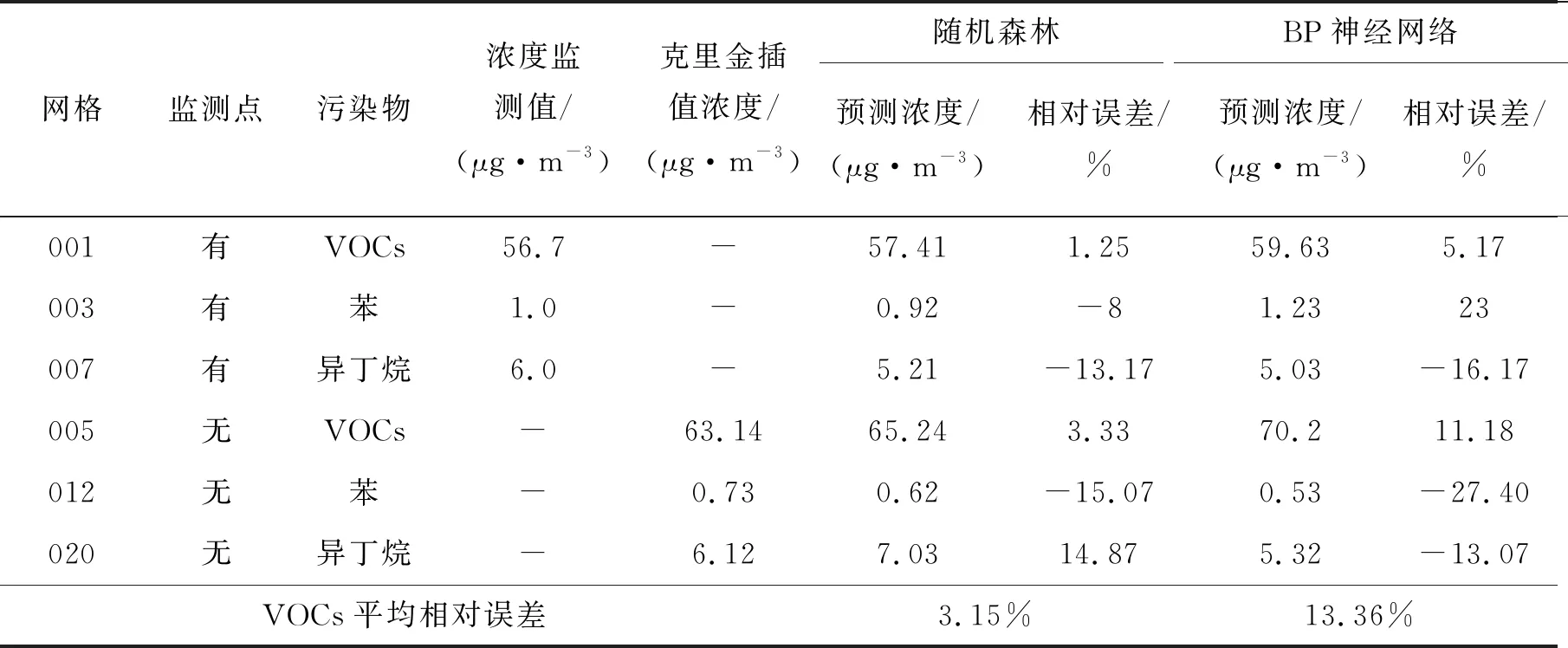
表8 不同预测方法的结果对比
5 结 论
本次预测是根据区域空间关联性以及VOCs污染物特征,对其浓度进行的精细化预测,意在解决监测设备不能普及部署以及区域之间污染物的流动影响问题。
1) 各区域之间的污染物存在相互影响。克里金插值法通过网格的空间地理位置来预估未设置监测点的网格数据;随机森林模型基于污染物特征之间的相关关系预测污染物的浓度,随机森林模型预测的结果更加精准。
2) 和BP神经网络模型相比,随机森林模型误差更小,其VOCs总浓度预测值的平均误差为3.15%。模型构建过程考虑了气象指标对预测结果的影响,更能体现出VOCs特征之间的关联性及相互影响作用。
3) 运用基于随机森林算法的预测模型预测区域VOCs总浓度,同时也可以预测其组成成分的浓度(如苯、甲苯、苯乙烯等),将其与国家VOCs排放控制标准限值进行对比,当超出限值时,结合区域网格编号信息[(pi,pj,pk),Num]获得其坐标信息(pi,pj,pk),而坐标定位位置可为管理者超前管控提供依据。

