局部存水空间对寒区隧道衬砌劣损特性的影响分析
马云峰,徐林生
(1. 重庆交通大学 土木工程学院, 重庆 400074; 2. 重庆水利电力职业技术学院,重庆 402160)
寒区隧道在修筑建设方面面临的技术问题较一般地区复杂得多,其中一个关键性的问题就是冻融和冻胀的影响[1]。在我国的寒区隧道中,非多年冻土隧道是分布最为广泛的一种,此类隧道多数围岩冻胀性很弱或是没有冻胀性,简单地用“隧道衬砌在围岩冻胀作用下开裂破坏”来解释寒区隧道冻害产生的原因是不准确的。在此类寒区隧道中,衬砌背后积存的水体冻胀引起的衬砌冻胀压力是造成冻害的主要原因。由于寒区隧道在开挖过程中开挖面的不规则性导致施工过程中常常没有做到围岩和衬砌结构紧密地贴合在一起,而是在衬砌和围岩之间留下局部存水空间。这种空间大多数存在于拱顶部位,主要是由混凝土浇筑工艺和混凝土在水化过程中自身体积变形引起的。
近年来,学者们除了对隧道围岩冻胀作用的影响进行了大量研究外,对隧道衬砌的冻胀破坏规律也进行了多方面的研究。王亚伟等[2]建立了两种衬砌背后空洞积水的冻胀简化模型,并对衬砌背后冻胀力的内力影响规律以及误差进行定量分析;李岩松等[3]利用复变函数理论引入一种求解考虑衬砌背后空洞积水的冻胀力和冻胀变形的方法;高焱等[4]利用室内模型试验,对隧道衬砌背后不同积水位置和积水体积的冻胀影响进行了分析。
本文在前人研究的基础之上,根据局部存水空间的特点,建立了水热力耦合冻胀模型,在验证模型可行性的基础上,通过数值模拟研究了衬砌存水空间作用位置、冻胀量等因素影响下,衬砌的应力变化及裂缝产生的部位、扩展的状态和分布的规律。
1 水热力三场耦合理论
1.1 基本假设
为了便于对劣损状态进行量化分析,做出假设:
1) 存水空间内的未冻土视为各向同性材料;
2) 不考虑水分由液态转向固态过程中热量的迁移;
3) 水变为冰的压力值不变。
1.2 三维非稳态热传导方程
根据热力学第一定律及传热学基本理论,存水空间内部温度变化遵循能量守恒定律,化简非稳态热传导方程可得[5]:
(1)
式中:T为存水空间温度;t为时间;α为衬砌的热扩散率;qv为单位时间内单位体积放出的热量;γ为衬砌的容重;c为衬砌的热扩散率。
1.3 温度场的离散化
在存水空间范围Ω,采用伽辽金法和加权残余法对热传导方程进行离散[6]:
(2)
式中:W为权函数;λ为衬砌的导热系数。
1.4 三维水分迁移控制方程
本文以压力水头来描述水分迁移的驱动力,以液态水的总体积来描述水分迁移的过程,根据质量守恒定律,迁移的过程遵循达西定律,最终简化的水分迁移微分方程为[7]:
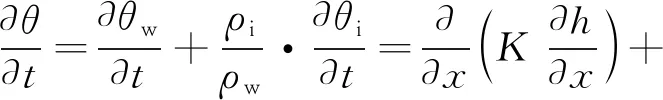
(3)
式中:θ为总体积含水量;θw为液态水体积含量;θi为含冰量;h为压力水头;K是非饱和土体内导水系数;ρw和ρi分别为水和冰的密度。
1.5 应力应变控制方程
1) 平衡微分方程
(4)
2) 几何方程
(5)
3) 物理方程
(6)
4) 当T<0 ℃时
(7)
式中:f为体应力;σ为正应力;τ为切应力;E为弹性模量;μ为泊松比;ε为正应变;∇u为位移矢量;εwi为温水耦合作用产生的应变。
2 ABAQUS有限元数学模型
2.1 定义形函数
(8)
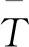
将式(8)代入式(2)中得到温度-渗流耦合方程(9),通过ABAQUS的求解器可以得到中心区域内节点的温度值。
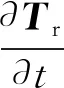
(9)
式中:Tr为温度列矩阵。
(10)
式中:β为介质表面的放热系数;Ta为外界温度;s是衬砌和存水空间的接触面积;e为存水空间和衬砌的集合。
在存水空间中隧道衬砌的冻胀破坏主要是由水体冻胀引起的体积变化而产生[8],根据应变增量法以及上述节点的温度值,按式(9)计算由蠕变和体积膨胀引起的等效节点荷载:
(11)
式中:Δ{εc}为蠕变应变增量矩阵;Δ{εv}为膨胀变形增量矩阵;v为存水空间范围;[B]为单元形函数;[D]为衬砌温度相关的塑性矩阵;结冰时,Δ{R}取正,融化时,Δ{R}取负。
2.2 定界条件
2.2.1初始条件
(12)
式中:Ti(i=r,w)分别为衬砌温度场的初始条件和存水空间内水流温度场的初始条件;T0为边界温度。
2.2.2边界条件
(13)
式中:n为法向;s(x,y,z,t)是接触面的表面积;λi(i=r,w)分别表示衬砌的导热系数和存水空间内水体的导热系数。
2.2.3边界耦合条件
衬砌和存水空间的交界面是耦合面,需满足以下两个条件[9]:
(14)
3 数值模型的可行性分析
数值模型以国道316线江洛镇至天水段八盘山隧道的主洞为原型。计算中为了凸显局部存水空间对隧道二次衬砌劣损性的影响,本文的数值模拟不考虑隧道埋深对隧道衬砌结构开裂的影响,主要考虑衬砌混凝土压溃、拉裂以及裂缝的延展导致的衬砌承载力失效。衬砌裂缝的扩展准则采用最大主应力失效准则[10]。数值模拟中采用ABAQUS中的XFEM模块模拟衬砌开裂,此法无需对裂缝进行预设,嵌入的cohesive单元层不依赖网格,可以模拟多裂缝的扩展和扩展速率。隧道衬砌网格采用六面体结构划分,单元类型为3D应力减缩积分单元,并在存水空间位置处网格加密,共划分单元65 654个,采用弹簧单元模拟围岩抗力。数值模型热物理学参数和衬砌的物理力学参数如表1、2所示。

表1 数值模型热物理学参数

表2 数值模型衬砌物理力学参数
八盘山隧道采用复合式衬砌,衬砌厚度为60 cm,隧道内轮廓为曲墙式等截面三心圆,拱顶高7.0 m,净宽10.5 m。结合长期的监控数据以及2018年八盘山隧道维修完善工程数据显示,该隧道衬砌环向裂缝23处,其中环向贯通裂缝约4处,缝宽在0.1~5.0 mm之间,缝长(除环向贯通裂缝)在10~130 mm之间,环向裂缝大部分存在渗水泛碱现象;衬砌纵向裂缝10处,其中边墙纵向裂缝4处,缝宽在0.2~0.3 mm之间,拱腰及起拱线纵向裂缝6处,缝宽在0.2~0.5 mm之间;衬砌斜向裂缝15处,缝宽在0.2~0.6 mm之间,缝长在5.0~16.0 m之间,斜向裂缝大部分存在渗水泛碱现象;衬砌交叉裂缝2处,主要集中于拱顶及边墙位置,裂缝宽度在0.2~0.5 mm之间,交叉裂缝均存在渗水泛碱现象。基于以上八盘山隧道衬砌裂损状况,选取其中一个监测断面,通过地质雷达和投入式静压液位计探明了该断面在拱顶处有存水空间,并探明了空间水体的位置和大小。为了验证数值模型模拟多场耦合作用下衬砌劣损的规律和适用性,选取拱顶处空间水体为类椭球体的工况进行对比验证。其中,模拟的类椭球体水体空间的静压和液面高度与实测存水空间相同。验证结果如图1、2所示。
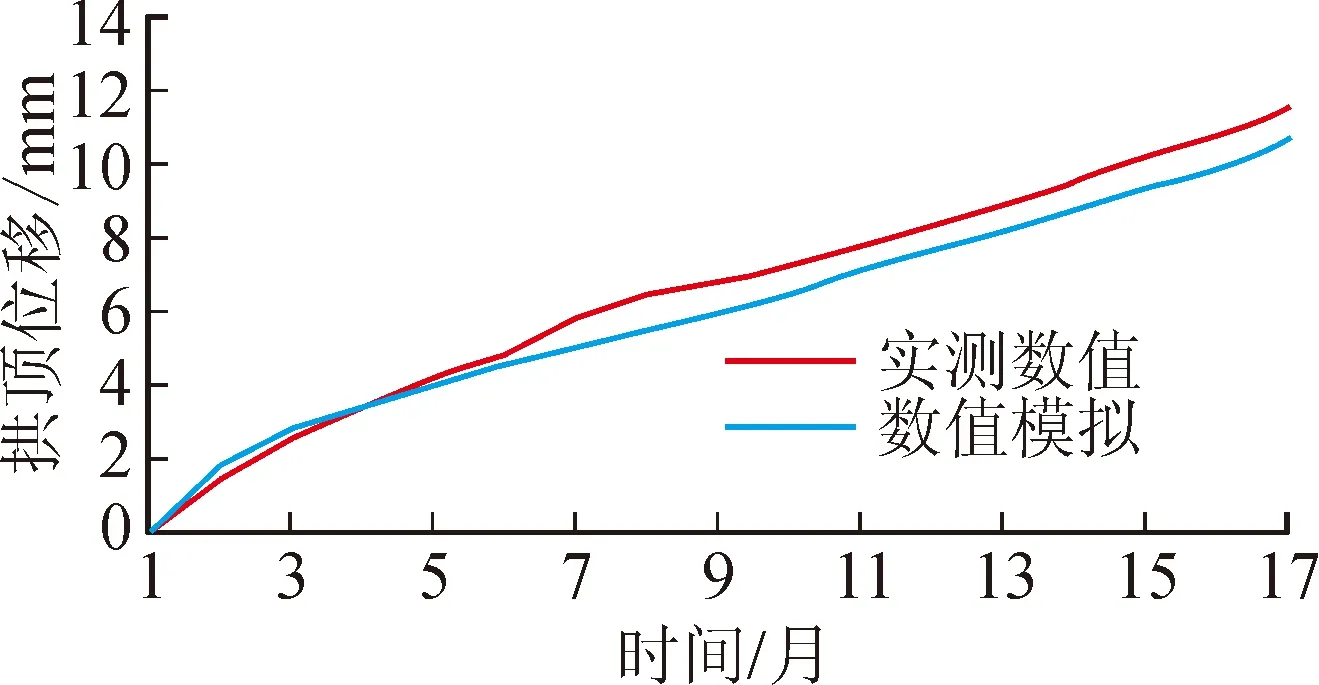
图1 数值模拟与监控数据的拱顶时间-位移曲线
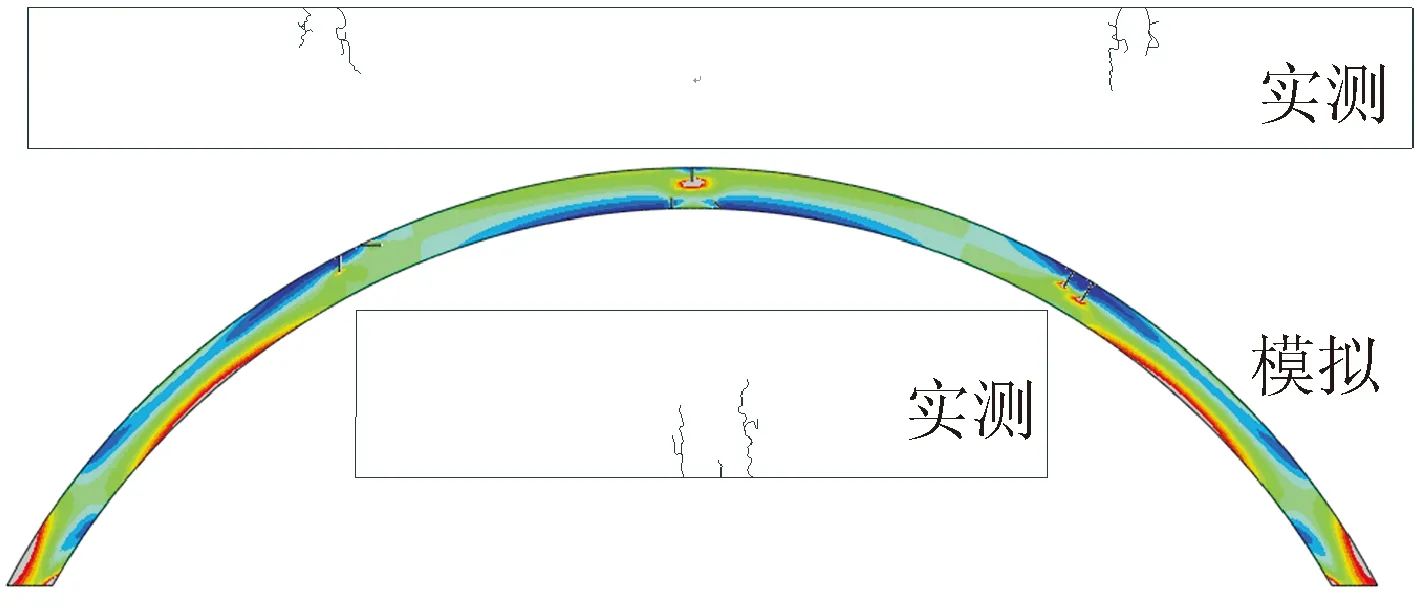
图2 数值模拟与实际监控裂缝分布状态对比图
图1、2分别是数值模拟与现场实测得到的拱顶沉降位移对比曲线和衬砌裂缝分布状态图。通过对17个月的拱顶位移值进行对比分析,结果显示实测数值较模拟数值略高,二者平均值差值低于实测值的5%,并且两数值曲线的拱顶位移扩展趋势基本一致。图2分析结果显示,从裂缝的分布状态和位置上看,二者的结果基本一致,并且实测裂缝的特征与数值模拟基本相同,内表面裂缝呈现出张拉特性,外表面呈现剪压特性。由此可见,采用本模型来模拟寒区隧道衬砌的劣损性是可行的。
4 寒区隧道局部存水空间的数值模拟
为了便于模型收敛计算,将存水空间假定为半椭球体,数值模拟的过程不考虑温度变化对衬砌结构应力的影响,只计算局部存水空间产生的冻胀附加应力和冻融循环对二次衬砌劣损性的影响。图3为局部存水空间的计算示意图。
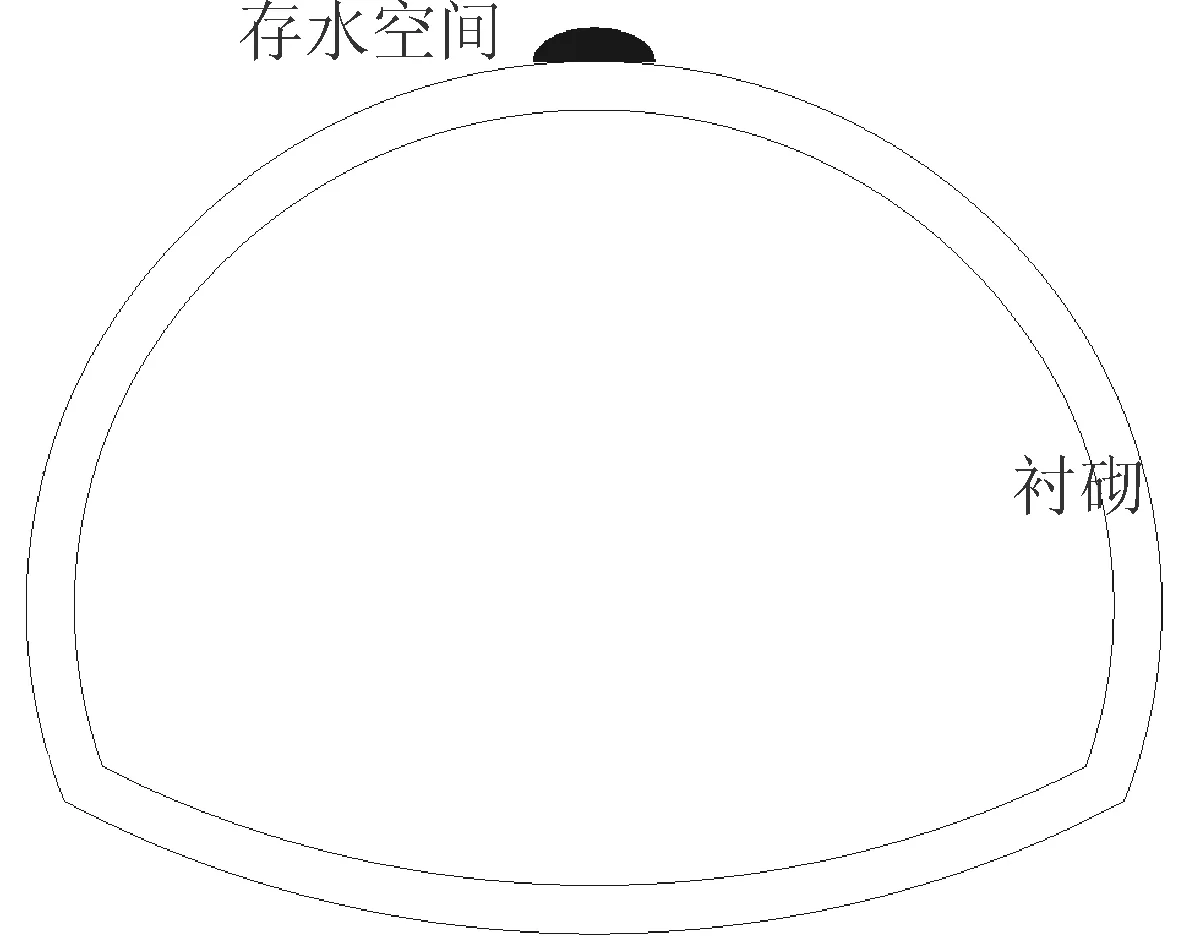
图3 局部存水空间计算示意图
4.1 存水空间位置对隧道衬砌劣损性的影响
考虑到隧道工程实际存水空间所在的位置,本文仅就拱顶、拱腰、拱脚和仰拱四处范围内的存水空间对衬砌劣损状态的影响进行分析。采用温度线性的加载方式对四种工况下裂缝的扩展状态进行对比分析,如图4所示。
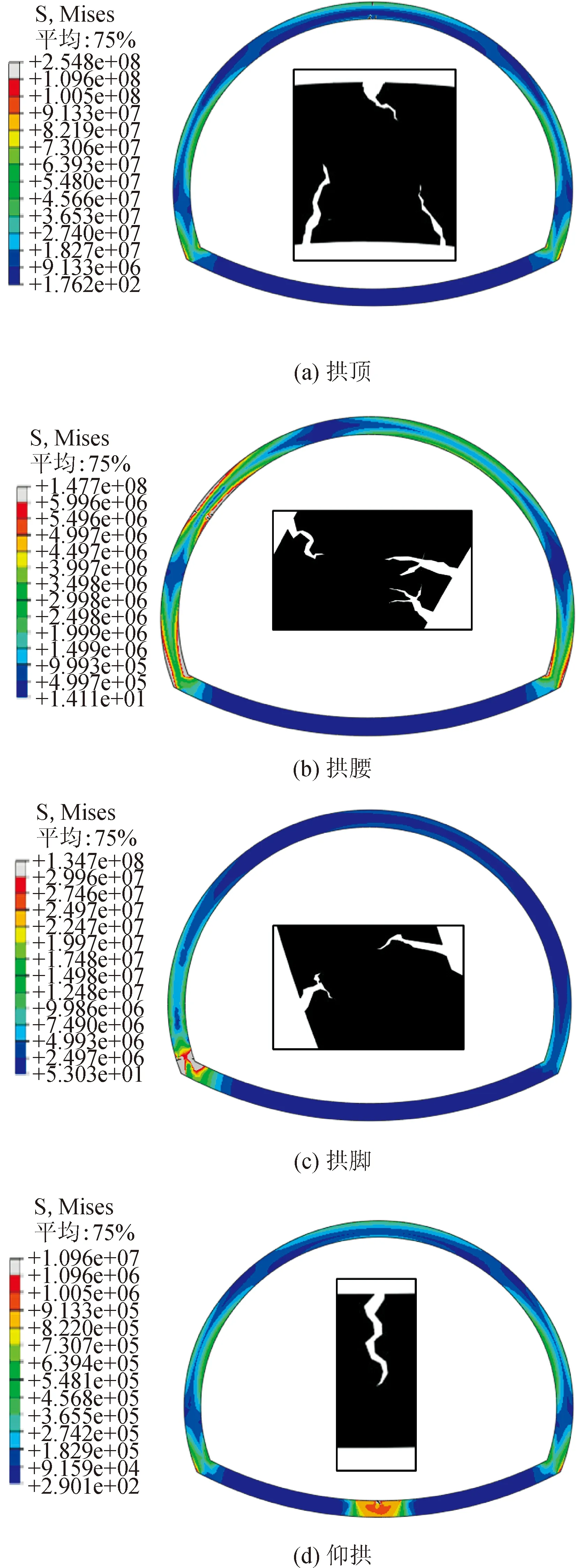
图4 局部存水空间作用裂缝分布状态图
由图4可以看出,四种工况下,产生裂缝的范围都集中在存水部位附近,并且在对应衬砌内表面位置均表现出明显的张拉特性;另外,在拱顶、拱腰和拱脚部位出现了不同程度的压溃型裂缝的起裂。拱顶位置在冻胀过程中内表面出现了较多裂缝,在开裂的过程中,裂缝的状态出现了起裂到闭合到再次开裂的情况,这表明衬砌在受力过程中呈现了剪拉交替的状态,这种状态除了出现明显的剪切破裂面外,同时还伴随着多处拉伸破坏线,这将极大地加速衬砌的劣化损伤进程。拱腰存水部位的冻胀也是一种偏压的作用,衬砌内表面的裂缝主要以张开为主,伴随着温度荷载的不断增加,裂缝的外观形式呈现出“X”状。拱脚处轴力和弯矩增大的过程中,轴力的增长速率大于弯矩的增长速率,呈现以轴力为主导,裂缝的扩展速率降低。仰拱存水部位在冻胀过程中在衬砌内表面出现一处延竖直方向扩展缓慢的裂缝,在衬砌的外表面出现了压力集中现象。
图5为衬砌裂缝开裂前后应力的分布状况,其中拱顶存水对衬砌劣损的影响最大。随着温度的降低,从应力的增长速率和裂缝的扩展速率上看,由大到小分别是拱顶、拱腰、拱脚、仰拱。
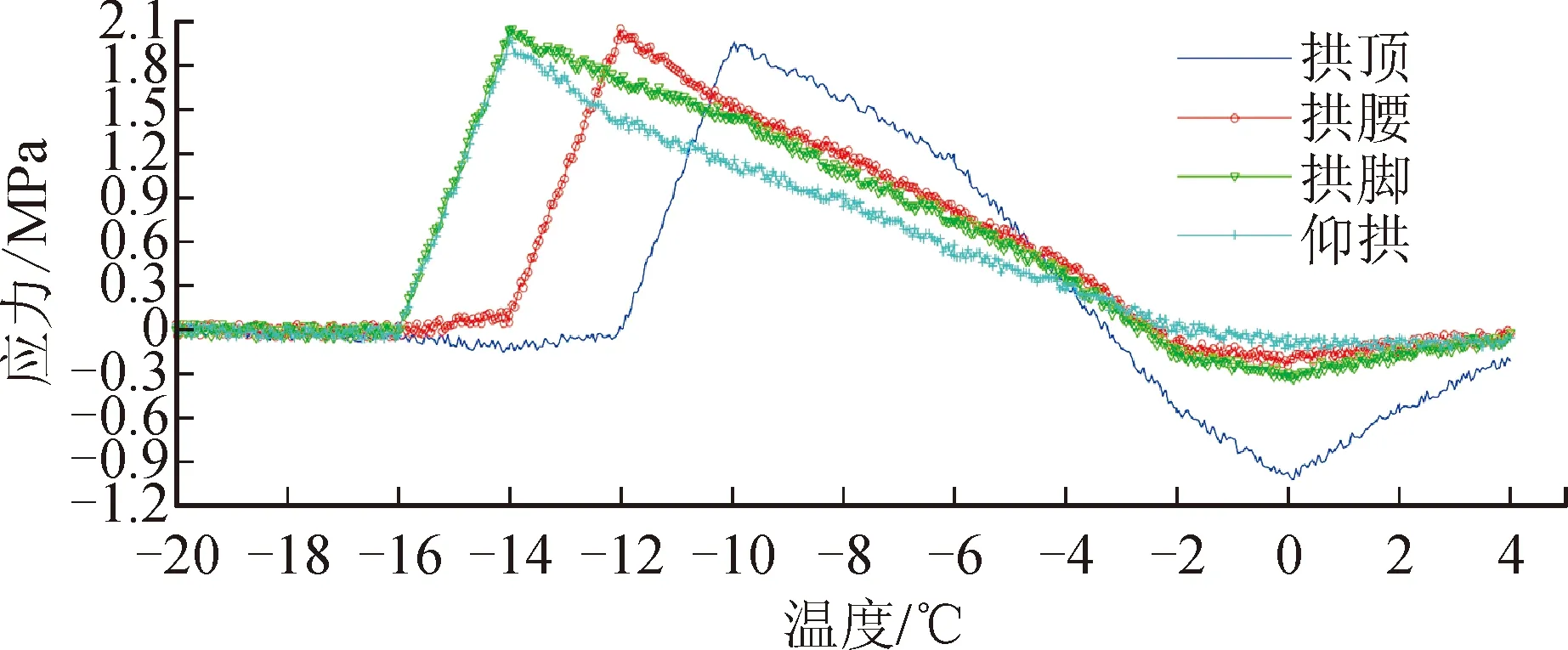
图5 裂缝开裂前后的应力分布规律
4.2 冻胀量对隧道衬砌劣损性的影响
为了描述寒区隧道衬砌的劣损性,选取拱顶冻胀量进行量化描述:
h=fZd
(15)
式中:h为冻胀量;f为拱顶平均冻胀强度;Zd为冻结面至衬砌外表面的法向距离。
八盘山隧道拱顶监测段数据显示,最大冻胀量约为6.7 mm,此时顶板温度为-12 ℃。本文分别在冻胀量为2 mm、4 mm、6 mm、8 mm四种工况下,分析存水空间对隧道衬砌裂缝的分布及开裂规律的影响,如图6所示。
由图6可见,当冻胀量为2 mm时,并未出现明显开裂迹象,但是衬砌内表面存在受压集中现象。当冻胀量达到4 mm时,衬砌的内表面出现开裂迹象,外表面的受压集中区域表现明显。当冻胀量增加到6 mm时,在衬砌内表面出现一处主裂缝且扩展较快,衬砌外表面有轻微压溃现象。当冻胀量继续增大到8 mm时,衬砌裂缝的分布发生变化,在拱腰附近的内外表面也出现多裂缝的扩展,拱顶出现局部压溃。由于拱顶内表面裂缝的持续扩展导致衬砌结构失效。
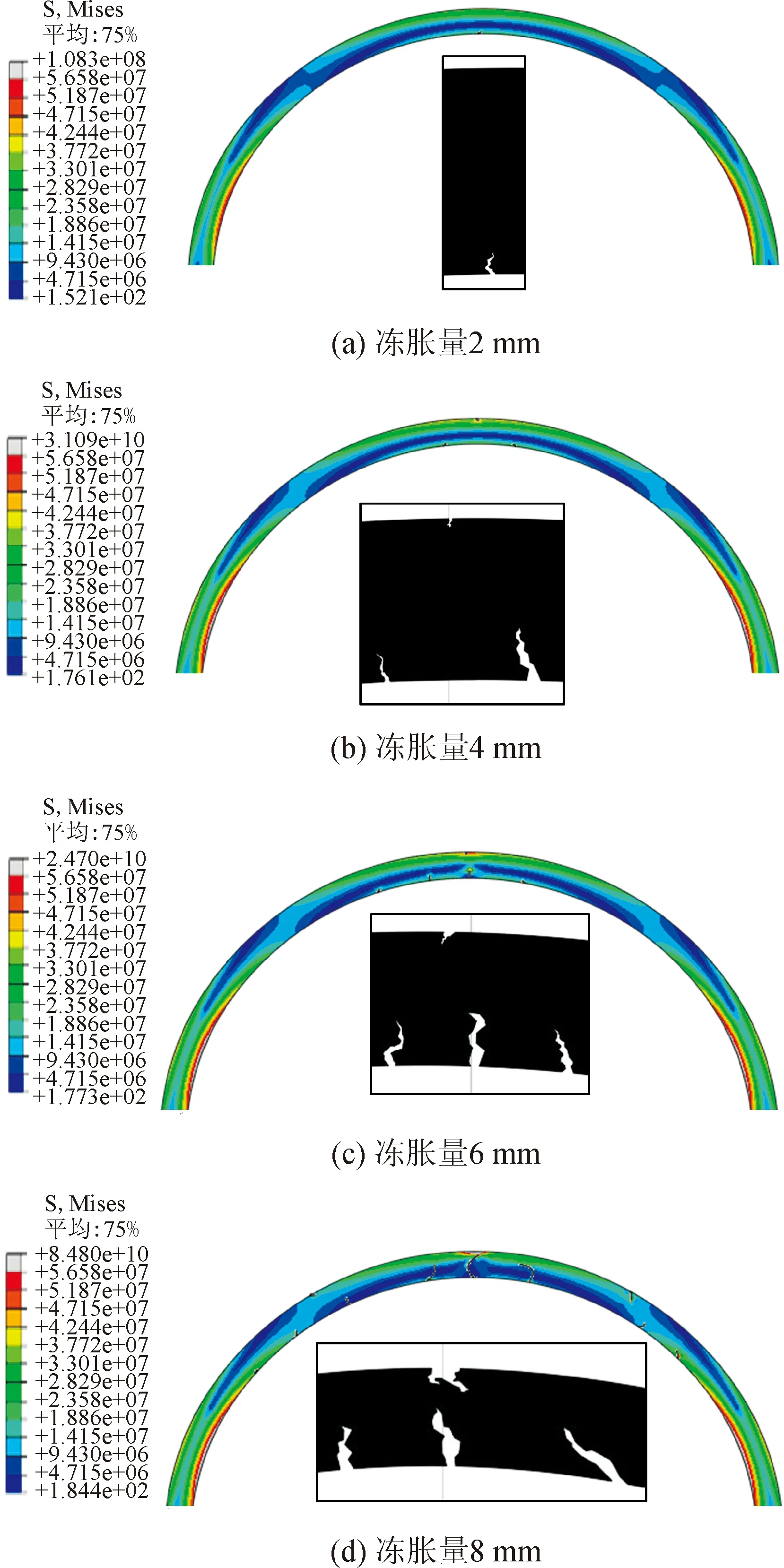
图6 不同冻胀量衬砌裂缝的开裂状态
冻胀量对衬砌应力的影响效果显著,同一冻融周期内,衬砌应力随着冻胀量的增长而增长。考虑到衬砌8 mm的冻胀量存在时间较短,分析24天内不同冻胀量下衬砌的开裂情况。
图7给出了衬砌拱顶内表面裂缝开裂前后的应力分布规律,在裂缝逐步扩展的过程中,衬砌内表面主要承受拉应力的作用,裂缝主要表现出张拉特性。应力的增长速率和裂缝的扩展速率随着冻胀量的增加而增大。
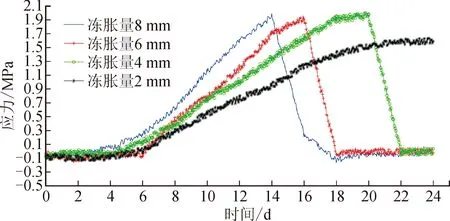
图7 拱顶裂缝开裂前后的应力分布规律
4.3 衬砌厚度变化对隧道衬砌劣损性的影响
本文以八盘山隧道衬砌厚度55 cm为基本模型、衬砌厚度30 cm为衬砌厚度不足模型、衬砌厚度70 cm为衬砌厚度增强模型,隧道的外径不变,分析拱顶在6 mm冻胀量状态下衬砌的劣损性,如图8所示。
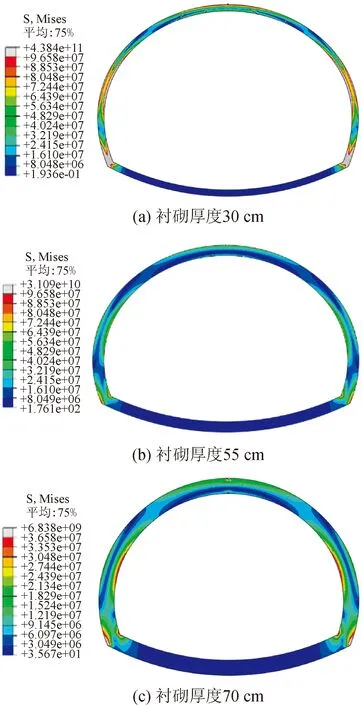
图8 不同衬砌厚度裂缝开裂状态
从图8中可知,在冻胀量加载的过程中,三种模型开裂的位置均分布在衬砌内表面,并呈现张拉特性。其中,衬砌厚度30cm模型产生的裂缝数量较多、宽度较大,裂缝的扩展范围从拱顶延伸至拱肩位置。
为了更好地反映衬砌厚度不足情况下衬砌的渐进劣损状态,输出整个模型的历程变化曲线如图9所示。在整个冻胀量加载过程中,55 cm和70 cm厚度衬砌应变能变化较为平缓,裂纹扩展基本处于稳态阶段;而30 cm厚度衬砌在冻胀量加载中后期,其曲线出现断层式跳跃并以更大的斜率不断增长,说明在此阶段裂缝已经进入扩展状态,并且裂缝在衬砌周身大面积扩展,衬砌的承载性能大幅度下降。
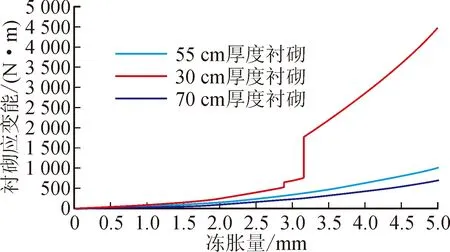
图9 整个衬砌应变能释放的历程曲线
5 结 论
1) 通过对检测监控数据的对比分析,本模型适用于模拟寒区隧道衬砌劣损开裂与裂缝扩展过程的量化分析研究。
2) 存水空间作用下,隧道衬砌结构在存水空间对应的中心区域产生的裂缝较为集中,且多表现为张拉型裂缝。从开裂前后的应力变化及裂缝的扩展状态来看,衬砌的劣损状态由强到弱分别为拱顶存水、拱腰存水、拱脚存水、仰拱存水。
3) 冻胀量的大小对隧道衬砌的应力和裂缝的扩展影响显著,隧道衬砌的劣损性随着衬砌冻胀量的增大而增大。
4) 与正常衬砌工况和加厚衬砌工况相比,在隧道衬砌厚度不足情况下,裂缝的扩展速率较快,应力的增长速率较大,并且整个衬砌产生的应变能远大于正常衬砌模型。

