浅谈小学数学开放性应用题的命制和评价

刘小会

【摘要】新课程理念强调：为了适应时代发展对人才的需要，数学课程需要特别注重发展学生的应用意识和创新意识.本文以三道小学数学开放性应用题为切入点，探讨这类题型的命制和评价.开放性应用题应源于教材，又不拘泥于教材.与其他应用题相比，开放性应用题更具灵活性、开放性和综合性，更能培养学生的应用意识和创新意识.

【关键词】开放性; 魔方; T字之谜;找规律

一、玩转五阶魔方，提升空间观念

在三维空间中，以边长为1 cm的正方体为基本构建块，组成我们熟悉的五阶魔方.通过设置不同的情境，分别求解该五阶魔方的体积和表面积.本题以小学生喜闻乐见的魔方为背景，把学生的认知水平由几何直观上升到空间想象和空间推演.问题梯度由易到难，层层递进.本题适用于五年级下学期及以上学段的学生.

正题：边长为1 cm的正方体组成一个五阶魔方：

（1）求出该五阶魔方（图1（a））的体积和表面积.

（2）如果在魔方内部抠掉一部分正方体，即打通魔方，形成5个洞，如图1（c）所示，求剩下部分的体积和表面积.

（3）在图1（c）的基础上，再抠掉最上面正中心处的方块（打通形成第6个洞，如图1（d）所示），求剩下部分的体积和表面积.

评价参考标准及建议：

（1）体积：5×5×5=125（cm3）.

表面积：5×5×6=150（cm2）.

评价细则：这一问不难，可以利用公式求出五阶魔方（边长为5 cm的正方体）的体积和表面积.

（2）体积：125-5×5=100（cm3）.

表面积：150+5×5×4-5×2=240（cm2）.

评价细则：①在第一问的基础上，用总体积减去抠掉部分的体积即可.5×5表示5个洞总共被抠掉的小正方体的数目.②5×4表示1个洞中魔方内部所增加的面数，5×5×4表示5个洞中魔方内部所增加的面数，5×2表示魔方表面减少的面数.

（3）体积：100-4=96（cm3）.

表面积：240+4×4-2-2=252（cm2）.

评价细则：①在第二问的基础上，用总体积减去抠掉部分的体积即可.4表示第6个洞被抠掉的方体数目.为什么是4而不是5呢？因为第6个洞和原来的一个洞在一个方块处交汇，所以这里不能重复计算.②此时这个问题已经比较复杂了，并且层层递进.在第二问所求表面积的基础上，解答此问的表面积.4×4表示第6个洞中，魔方内部（4个方块）所增加的面数，第一个2表示魔方表面减少的面数，第二个2表示交汇处减少的面数.

二、巧解T字之谜，探寻组合奥秘

本题属于数学好玩的范畴，以民间智慧“T字之谜”为数学背景，探讨组合图形的构造、面积计算和形状多样性等问题.类似于七巧板，“T字之謎”也属于智力拼板玩具，但只有四块，所以也称“四巧板”，与七巧板性质相同.“T字之谜”的组合过程着重考查观察能力、动手能力和衔接能力.本题适用于五年级下学期及以上学段的学生，重在开拓思维和发散想象，答案具有多样性和开放性.

正题：“T字之谜”由四块不同形状的单元块组成：一个等腰直角三角形①、一个不规则五边形②、一个短直角梯形③、一个长直角梯形④.如图2所示.

（1）把这四个单元块组合成“T”字，画出示意图，并计算总面积.（2）计算不规则五边形②的面积.

（3）“T字之谜”中的四块单元块还可以组合成其他图形吗？请列出两种形状.

评价参考标准及建议：

（1）四块单元块拼接成两个长方形，组成“T”字.“T”字如图3（1）所示.对应的T字面积：1×3+1×3=6（cm2）.

（2）不规则五边形②的面积计算如下：

方法一：②的面积=T的面积-①的面积-③的面积-④的面积=6-0.5-1-2.5=2（cm2）.

方法二：把五边形分割成一个平行四边形和一个三角形，如图3（2）所示.根据第一问中“T”字的组成形式，得出平行四边形的高和三角形的底.

②的面积=1.5+0.5=2（cm2）.

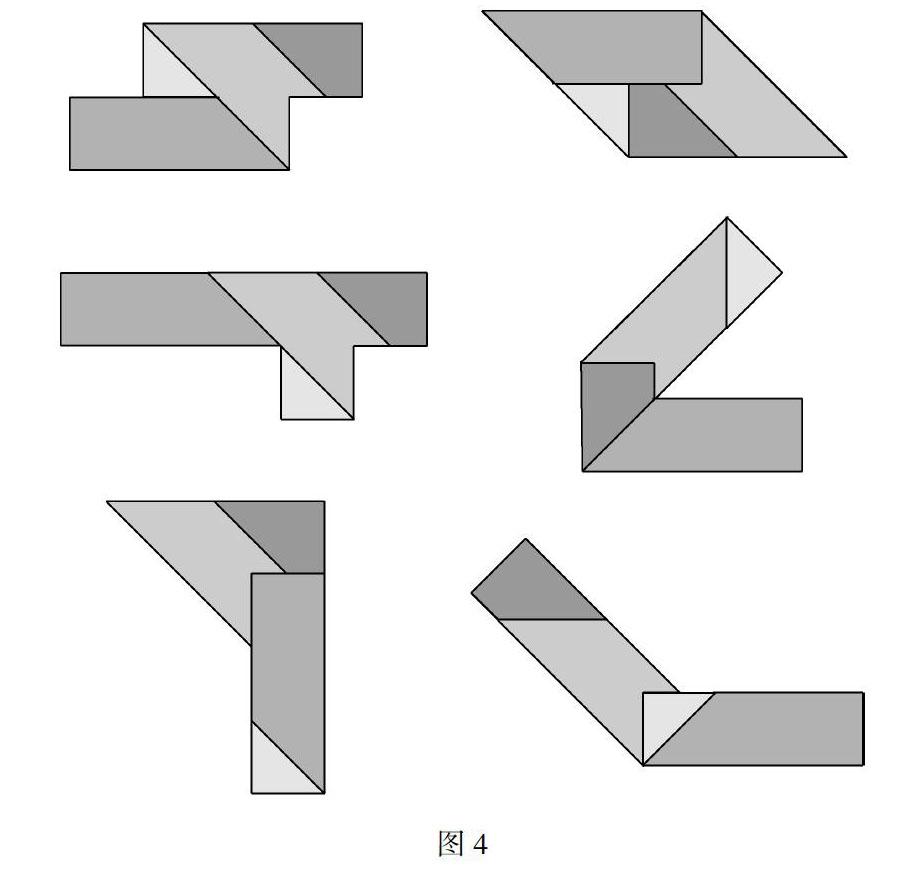
（3）此问具有开放性，答案不唯一.组合的关键在于把长度相等的边拼接在一起.图4中展示了6种形状，方法多样，巧妙有趣.事实上，目前“T字之谜”的拼凑有上百种情况，是老少皆宜的休闲智力玩具.

三、构造方形串联，挖掘潜在规律

本题利用分割法、观察法和找规律法解决求复杂图形面积的问题.学生体验图形形状变化与面积大小变化关系的同时，通过猜想和归纳找到形与数之间的关系.本题适用于五年级下学期及以上学段的学生.

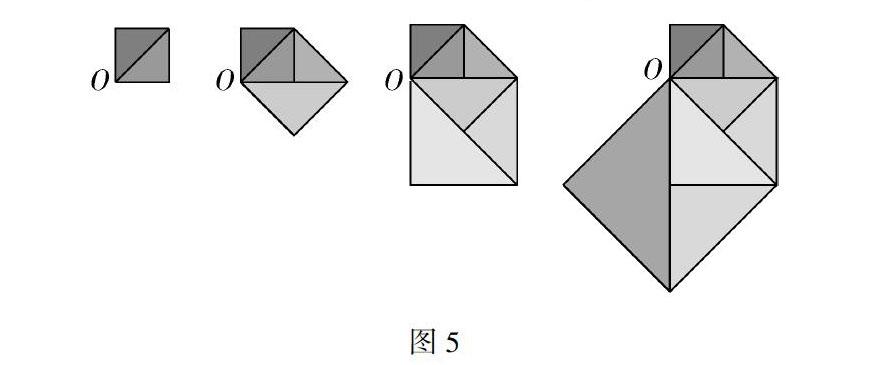
正题：从边长是1 cm的正方形开始，从O点出发，以正方形的对角线为边顺时针连续画正方形，如图5所示：

（1）画出第5个正方形，并求出边长.

（2）用两种不同的方法求画第5个正方形时所得图形的总面积.

（3）综合5幅图，在计算图形总面积的过程中，你可以找到一些规律吗？

评价参考标准及建议：

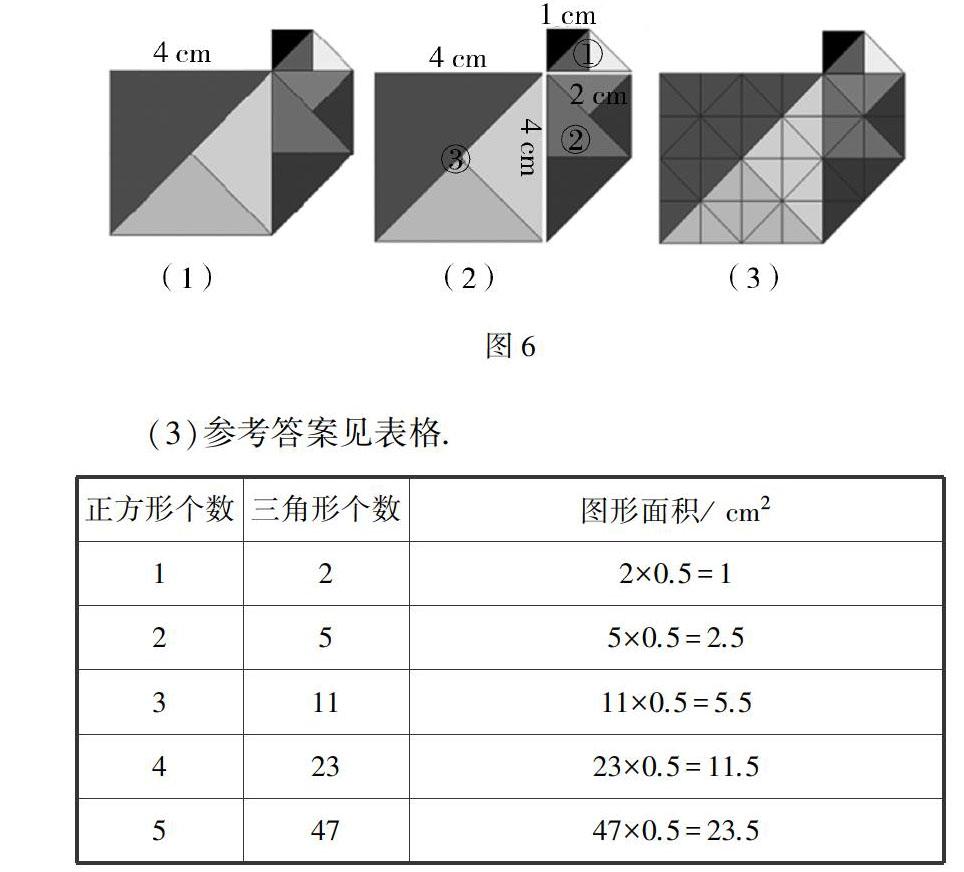
（1）画出第5个正方形，如图6（1）所示，边长为1×4=4（cm）.

评价细则：以第4个正方形的对角线为边，画出第5个正方形.通过观察，发现此时的边长为4个1 cm.

（2）面积计算参考方法（不限）如下：

方法一：图形可以分割成如图6（2）所示的三部分，分别计算求和即得总面积.

面积=①+②+③=1.5+6+16=23.5（cm2）.

方法二：图形可以分割成如图6（3）所示的47个完全一样的小三角形.

面积=47×0.5=23.5（cm2）.

（3）参考答案见表格.

这个规律有点类似于斐波那契数列，利用前一类信息，计算下一类信息.文字描述如下：

后一个图形三角形的个数=前一个图形三角形的个数×2+1，对应数学表达式为：f（n+1）=2f（n）+1，f（1）=2，f（n）=3×2n-1-1.

四、结束语

开放性应用题的探讨就像一段旅行，其终点不是让学生获得一堆零散、呆板和固定的知识，而是让他们能够积极、充分、灵活地运用数学知识去发散思维、解决问题并且学以致用，由此获得人格的健全和精神的成长，成为新时代的社会主义建设者和接班人.此外，应用意识和创新意识的培养应该从义务教育阶段做起，并贯串于数学教育的始终.