基于数字孪生的装配过程质量控制方法*

郝博，王建新，王明阳，赵阳，徐东平

(1.东北大学机械工程与自动化学院，沈阳 110819； 2.东北大学秦皇岛分校控制工程学院，河北 秦皇岛 066004)

0 引言

“Digital Twin”(数字孪生)这一概念最早于2003年出现在美国密歇根大学Grieves教授的一次课程中，并在后续文章中将它定义为包含实体产品、虚拟产品以及二者之间的连接的数字化系统[1]。近年来随着国内外学者的研究数字孪生的定义日趋完善，目前比较认可的是由北京航空航天大学、北京理工大学等给出的定义：数字孪生是利用数字技术创建物理实体的虚拟模型，借助数据模拟物理实体在真实环境中的特征、行为、形成过程和性能，通过虚实交互反馈、数据融合分析、决策迭代优化、精准高效执行等手段扩展物理实体的能力[2-3]。

近年来物联网，大数据，云计算，智能车间，5G通信等技术快速发展，国内外学者在数字孪生的研究方面取得了一些成果。郭飞燕等[4]对数字孪生驱动的装配工艺设计进行了研究，提出了数字孪生模型驱动的航空产品装配工艺优化-反馈-改进环机制；斯图加特大学Behrang Ashtari Talkhestani等[5]提出基于模型融合的数字孪生建模方法，通过多种数理仿真模型的组合构建复杂的虚拟实体；洛克希德·马丁公司[6]创建了“数字线”的工作方式，通过采集物理空间的多源异构动态数据，建立与现实空间中的物理实体完全一致的数字孪生体模型，对其进行仿真、分析和预测实体产品在现实空间中的状态；周石恩[7]提出了基于数字孪生的复杂产品装配建模与精度分析方法，考虑特征配准和物理干涉等情况预测薄壁件真实装配误差，指导实际薄壁件的定位和装配操作。Liu Chao[8]和Park K T[9]等指出第四次工业革命的核心概念网络物理系统(CPS)与数字孪生技术的关联，数字孪生作为虚拟工厂，可表示为网络物理生产系统(CPPS)技术应用的生产现场，能够克服个性化生产过程的限制。目前，我国的数字孪生技术仍处于探索阶段，仍存在一些问题在实际应用中没有得到很好的解决。

本文针对飞机机翼翼盒的装配过程，提出装配过程质量在线补偿及精准控制方法，依托数字孪生车间的各种数字化装配和检测设备对装配数据进行实时采集和分析，在研究和分析装配过程的历史质量数据的基础上，通过Copula理论构建质量控制点之间的相关性模型，再借助装配质量熵和互信息理论构建产品装配稳定性测度模型[10-12]，预测并给出下一步的最优化装配方案，并将最佳方案传输至装配现场，实现减小累计误差，提高装配质量，降低返修率。最后，在某车间以某型号机翼翼盒装配为例，对原型系统进行应用验证。

1 基于数字孪生的装配过程质量优化模型

本文提出基于数字孪生的装配过程质量优化模型主要包括以下4个方面：物理车间、虚拟车间、数据中心和装配车间质量控制系统，如图1所示。

图1 基于数字孪生的装配过程质量控制模型

(1)物理车间：本文中的物理车间是指装配车间，包括由装配产品所需的装配物料、装配和检测设备、人员、正在装配或已经装配完成的产品等组成的真实物理空间。

(2)虚拟车间：按照物理车间的真实拓扑关系或几何关系构建的函数模型，工艺规则以及车间模型、工位模型设备模型、产品模型等二维布局或三维模型。可以通过构建Copula函数的质量控制点相关性模型对装配过程进行优化。

(3)数据中心：主要负责数据的传输和存储工作，包括数据总线和孪生数据。其中数据总线主要是用于数据传输的现场总线、数据接口、智能网关等。孪生数据包括在物理车间内通过三坐标测量仪、温度传感器、震动传感器、角度传感器、速度传感器、力传感器、位移传感器等数字测量设备自动或人工进行采集的数据和在工程软件中的模拟仿真数据。

(4)装配车间质量控制系统：包括各种装配设备的控制软件(如实例中使用的SD-TBC350L型物联网螺丝刀的控制面板)、数据处理分析程序软件和其他企业级车间管理软件。技术人员可以通过装配车间管控系统对装配过程进行干预。

过程如图2所示。装配过程开始后，装配人员按照工艺流程操作，装配同时按照规定的装配质量数据采集要求，通过三坐标测量仪、温度传感器、震动传感器、角度传感器、速度传感器、力传感器、位移传感器等数字测量设备自动或人工进行数据采集，然后通过现场总线和数据接口将数据传输至数据中心进行存储。通过装配车间质量控制系统的程序软件对这些数据进行处理，构建Copula函数质量控制点相关性模型对存储的数据进行实时分析，借助装配质量熵和互信息理论构建产品装配稳定性测度模型，对下一步操作的控制阈[10]进行优化，选取最佳工艺参数，最后将结果通过数据中心传输到物理车间。

图2 基于数字孪生的装配过程质量优化流程

2 基于Copula函数的装配过程质量优化

2.1 Copula质量控制点相关性模型构建

Copula函数由Sklar A[12]首先提出应用在数学和统计定理描述，又被称为连接函数，通过Copula函数将各变量间的联合分布和它们的边缘分布联合在一起，描述不同变量之间的相关关系，其定义为：令C：[0，1]n是定义在[0，1]上的n维联合分布函数，如果C的边缘分布函数分别是定义在区间[0,1]上的均匀分布函数，则称C是一个n元Coupla函数，n=1，2，3，…。由此定义可知Copula函数可以包含很多种类。

质量控制点是在产品装配过程中为了保证装配最终质量需要控制的装配工艺规范，比如飞机机翼翼盒铆接过程中的拉力和位移，螺栓拧紧时的扭矩，各种零部件的尺寸等。使用Copula函数建立的装配过程质量控制点之间的相关性模型可以表达不同质量控制点之间的相关性关系，如图3所示，Si为装配工序，按照规定工序S={S1，S2，…，Sn}顺序装配，每项工序中包含装配工艺规范，αj为质量控制点，α={α1，α2，αj，…，αm}为工序Si的m个质量控制点，由机械产品装配过程的特点可知，前后质量控制点之间相互影响，最终影响该工序的完成质量。

模型的建立主要分为四步：①通过对装配完成且已合格产品的历史质量控制点数据进行分析，估计前后质量控制点的边缘分布函数；②绘制频数直方图和频率直方图，根据图形特点选择Copula函数；③Copula函数未知参数估计；④对函数模型进行评价，选取最优函数，并可得到其函数对应的概率密度函数，令其为f(xi)。

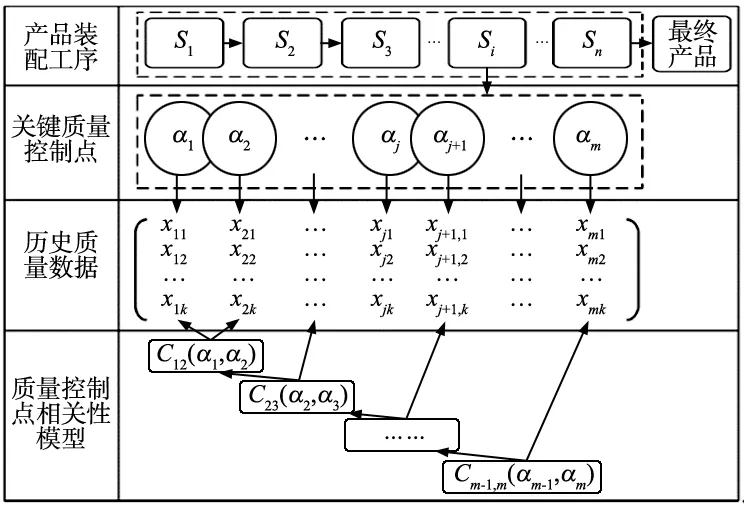
图3 Copula质量控制点相关性模型

2.2 质量控制点控制阈优化

控制阈是指装配工艺规定中所要求的工艺参数范围，比如螺栓拧紧的扭矩为(24±2)N·m，标准值为24 N·m，上下浮动范围2 N·m。根据装配要求将质量控制点αi分为k个控制阈，从小到大依次为[ri0,ri1), [ri1,ri2),…, [ri,k-1,rik),其中αij表示[ri,j-1,rij)，j=1，2，…，k，装配工具的精度、工人技术水平和熟练程度等因素都可以影响k值的大小，工具设备越精密、工人技术水平越熟练，k的值越大。前后吮吸质量控制点之间相互影响，因此选择合适的控制阈可以对装配质量达到优化的效果。通过装配质量熵AQE[13]的方法对其进行优化选择，设质量控制点αi对应的概率密度函数为f(xi),那么质量控制点αi的AQE如公式所示为：

(1)

其中，a、A是与质量控制点相关的常数，Xi的定义域为S，H(Xi)是对概率分布的无偏估计，可应用该参数预测下一装配质量控制点的数据，其度量方法不受变量xi的分布的影响，可以实现不同种装配质量控制点之间的比较，可以支持误差积累传递、累计研究。定义互信息用于表征两者或者更多控制点间相关性的大小，公式为：

(2)

I(Xi;Xi-1)=I(Xi)-I(Xi|Xi-1)

(3)

其中，I(Xi;Xi-1)表示的是Xi和Xi-1之间所的共享的信息量，在产品装配过程中，它可以用来体现控制点αi-1处的装配工作完成后其对下一控制点αi处装配质量控制不确定度的影响，一般情况下为正面影响即减小不确定度。因此，我们可以根据控制点之间的相关性，利用工序靠前的质量控制点的装配结果来对工序靠后质量控制点进行装配优化。I(Xi)表示控制点αi的装配质量不确定度，I(Xi;Xi-1)表示的是控制点I(Xi)在利用控制点αi-1装配信息后的装配质量不确定度。在这些公式和定义的基础上建立装配稳定性指数测度模型[11]，公式为：

(4)

R(αi|x∈αi)=1-I(Xi|Xi-1)/H(Xi)

(5)

其中，αij表示的是第i个控制点的j个控制阈。P(αij|αi-1)表示在第i-1个控制点装配完成后，第i个控制点第j个控制阈的装配成功率。R(αi|xα)表示不确定度减小的比例，由分析大量历史装配数据获得。V(αi|xαi)表示装配的稳定性，其值越小，代表装配波动范围越小，即越稳定；反之，其值越大，代表装配波动范围越大，即越不稳定。

3 以机翼上的某组螺栓装配为例

飞机结构复杂，在装配过程中包含几万个甚至十几万零部件，装配过程复杂，飞机结构件的装配质量与其偏差源之间呈现非线性、多层级强耦合、不确定度大的传递关系,难以通过构建装配尺寸链方程的方法诊断出影响装配质量的关键偏差源[14-15]，所以针对某型机翼装配构建模型进行分析，机翼上壁板对接构件如图4所示，以1号螺栓U和5号螺栓V为例。

图4 上壁板对接构件 图5 SD-TBC350L型物联网 螺丝刀和PF50控制器

装配过程开始后，装配人员按照工艺流程操作，使用SD-TBC350L型物联网螺丝刀(设备如图5所示)将螺栓1拧紧并通过物联网螺丝刀测定扭矩为24.5 N·m。此数据通过PF50控制器的以太网接口将数据传输至数据中心进行存。分析装配合格且实际性能良好的500件产品进行历史质量控制点数据分析，构建Copula函数质量控制点相关性模型。部分数据如表1所示。

表1 部分螺栓扭矩

利用Matlab进行分析处理各种数据，按照2.1节的过程估计前后质量控制点的边缘分布函数,可绘制频数直方图和频率直方图，如图6所示。

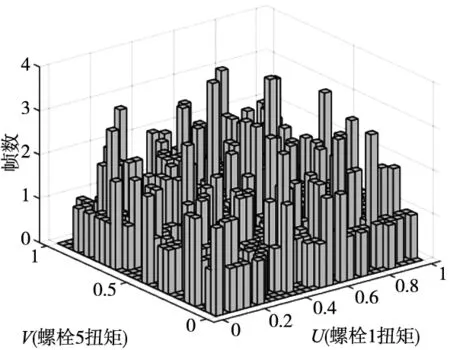
(a)二元频数直方图

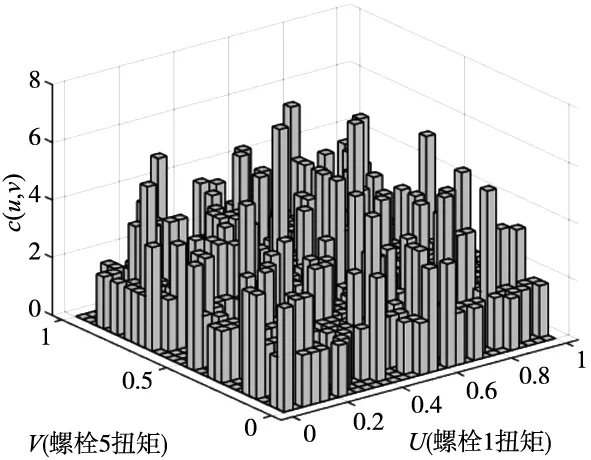
(b)二元频率直方图 图6 频数直方图和频率直方图

分析图形特征，最终选取二元t-Copula函数，绘制二元t-Copula的密度函数和分布函数图如图7所示。

(a)密度函数图

(b)分布函数图

估计未知参数后可得t-Copula函数公式为：

(6)

根据2.2节的方法，两颗螺栓紧固扭矩规范标准为(24±2)N·m，将质量控制点分为4个控制阈，从小到大依次为[22，23)， [23，24)， [24，25)，[25，26]。分别计算下一个需要拧紧的螺栓5的不同扭矩控制阈对应的V(αi|xαi)值，计算结果如表2所示。

表2 螺栓5各控制阈的稳定性值

从表2看出，控制阈[25，26)对应的V(αi|xαi)值最小，故选取控制阈[25，26)为最佳装配质量控制阈。整个计算过程在虚拟车间快速进行，最后将最佳装配质量控制阈的结果通过数据中心以太网接口传输到物理车间物联网螺丝刀控制器，自动设定物联网螺丝刀扭矩的上下限，当扭矩不足25 N·m时则会报警提示装配人员，当扭矩峰值达到26 N·m则会自动停止工作。接下来重复这一流程直至全部螺栓拧紧后结束。

4 结论

本研究针对飞机机翼翼盒的装配过程，提出装配过程质量在线补偿及精准控制方法，通过验证可得以下结论：

(1)依托数字孪生车间的各种数字化装配和检测设备对装配数据进行实时采集和分析，在研究和分析装配过程的历史质量数据的基础上，可以通过Copula理论构建质量控制点之间的相关性模型。

(2)借助装配质量熵和互信息理论构建产品装配稳定性测度模型，可以预测并给出下一步的最优化装配方案。

(3)通过现场总线和数据接口，可以将最佳方案传输至装配现场，最终实现减小累计误差，提高装配精度和产品质量，降低返修率。但是，目前像飞机机翼这种复杂装备产品的数字孪生技术和装配过程质量控制方法仍处于探索阶段，基于数字孪生的装配质量控制方法作为一种新方法，还需要进一步研究完善和验证。