节理化层状岩质边坡变形效应及稳定性分析

徐 盼，程 策，潘松悦，邵开京，潘永建

（铜陵学院 建筑工程学院，安徽 铜陵244000）

随着我国基础建设的快速发展，工程实际中遇到了大量岩质边坡工程的稳定性问题，引起了广大学者的关注。由于露天岩质边坡层中存在大量发育的不同构造、软弱夹层和节理等，构成了岩层的软弱结构面，该类边坡中，裂隙的产生、发展、贯通以及节理间的相互作用，显著影响了节理化岩体的强度和变形，从而严重影响边坡稳定性，给边坡开挖与支护带来困难［1-3］。目前，对于节理化边坡稳定性的研究分析方法主要有实验室试验及数值模拟法。杨圣奇［4］开展了断续节理砂岩试样在单轴压缩试验下的宏观变形与裂纹扩展之间关系的研究；Heng等［5］的直剪试验研究总结了不同倾角的层状岩石在压剪作用下存在四种破坏模式；杨忠平等［6］采用振动台试验结合UDEC数值分析方法，研究了两类不同形式的典型岩质边坡在反复微震作用下的稳定性；蒋明镜等［2］将微观接触模型导入PFC软件中，并基于重力增加法对顺层、反倾两类岩质边坡的失稳演化过程进行了模拟；贺续文等［7］通过离散元软件，对节理岩体边坡的力学性能进行了研究，并分析了节理连通率对边坡失稳破坏形式的影响；韩廷文等［8］利用GeoStudio软件对节理化高陡边坡在地下水和地震作用下的稳定性进行了定量分析。

本文采用离散元方法，利用非连续介质程序UDEC，分别建立水平层理和顺缓层理两类岩质边坡计算模型，考虑了降雨渗透因素的影响，分析含有节理面的岩质边坡变形效应，并进一步讨论了层理倾角对节理边坡稳定性的影响，为工程实际中类似节理化层状边坡的设计和支护提供一定参考。

1 UDEC常用本构模型

UDEC程序增加了非连续介质的力学分析方法，因此能够分析非连续介质材料（如节理岩体）的滑移、裂隙张开及垮落等大变形问题。

1.1 块体本构模型

UDEC的岩石破坏基本准则为M-C准则［9］，与此对应的是剪切破坏的线性破坏面，应力为：

式（1）中，σ1为最大主应力；σ3为最小主应力；c为黏聚力；φ为内摩擦角。

若fs＜0，则发生剪切破坏。但当法向应力变为拉应力时，此时M-C准则不再适用，程序为简化计算，屈服面将扩展到最小主应力σ3等于极限抗拉强度σt的区域。

1.2 节理本构模型

对于不连续面（即接触面），UDEC有四种节理本构模型，分析边坡稳定性时常用的是面接触库伦滑移模型。接触面的塑性剪切破坏准则为：

式（2）中，σs为切向应力，用切向应力增量 Δσs表示，Δσs=Ksδs（Ks为切向刚度系数，δs为相对位移）；σn为法向应力，σn=Knδn（Kn为法向刚度系数，δn为法向嵌入值）。

2 数值计算模型与模拟方案

2.1 数值计算模型

某砂岩边坡，坡高30 m，开挖后坡角为45°。由于模型尺寸效应对计算结果有一定影响，取坡脚至左侧边界的距离为30 m，坡肩至右侧边界距离为34 m，坡脚向下边界延伸15 m。根据优势结构面的产状和组合情况，开挖后形成水平层理、顺缓层理两类岩质结构边坡。边坡竖向节理间距为5 m，水平及顺层层理间距均为3 m，顺层层理倾角20°。边坡左侧水位高15 m，右侧水位高42 m。两类边坡数值计算模型及节理面构造见图1，数值计算采用的物理力学参数及水力学参数见表1、表2。

2.2 模拟方案

首先，分别分析上述两类岩质边坡在自重作用下的变形稳定性，揭示不同节理面控制下的边坡位移及裂隙产生与发展趋势；其次，引入降雨渗透作用，进行流固耦合分析，反映水力学作用对顺层层理边坡稳定性的影响，并进一步分析边坡稳定性随层理倾角的变化。

图1 计算模型及边坡节理面示意图

表1 砂岩及节理面参数

表2 水力学参数

3 模拟结果分析

3.1 边坡结构变形效应分析

边坡位移矢量图如图2所示。

图2 边坡位移矢量图

由图2可知：边坡开挖后，在相同计算步数下，水平层理边坡向坡面临空侧产生了卸载回弹现象，回弹量沿坡面呈递增趋势，最大回弹量为6 mm，坡底也出现了轻微隆起；顺缓层理边坡表现为沿着层理方向的楔形滑移，出现滑移-拉裂，坡脚处位移最大，达到136 mm，远大于水平层理边坡位移量，但坡底几乎不隆起。可见，边坡岩体结构显著影响着边坡变形形式及位移量。

边坡岩体剪切位移如图3所示，边坡岩体裂隙新生与张开分布如图4所示。

由图3（a）和图4（a）可知：边坡开挖后，水平层理边坡内的竖向剪切位移比水平剪切位移大，竖向剪切位移量自上而下呈现递减趋势；坡体呈现拉裂破坏，并存在明显的竖向张开裂隙，裂隙长度约为18 m，主要分布在坡顶至坡脚处。

由图3（b）和图4（b）可知：边坡开挖后，顺层层理边坡沿滑移面产生的最大剪切位移为111 mm，在坡体内可见明显的过坡脚的楔形滑移体轮廓，滑移面延伸到坡脚以下约5 m处，故应对坡脚处进行加固处理。与水平层理边坡相比，顺层层理边坡的新生张开裂隙范围增大了约50%。由此可见，顺层层理边坡的稳定性明显较差。

图3 边坡岩体剪切位移图

图4 边坡岩体裂隙新生与张开分布图

3.2 降雨作用对顺缓层理边坡稳定性的影响

在降雨作用下，边坡位移矢量图如图5所示，边坡岩体剪切位移如图6所示，边坡岩体裂隙新生与张开分布如图7所示。

图5 边坡位移矢量图

图6 边坡岩体剪切位移图

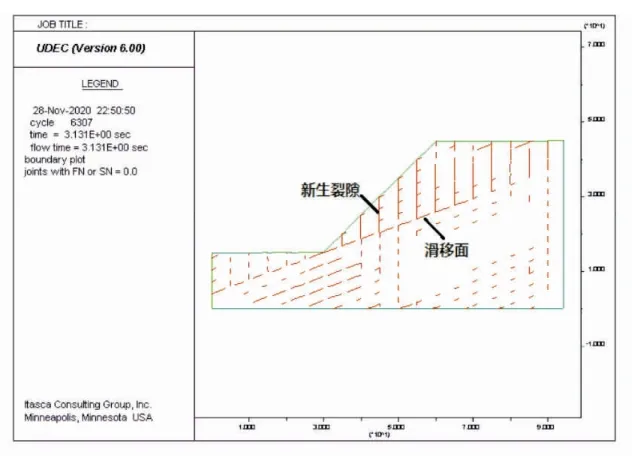
图7 边坡岩体裂隙新生与张开分布图

由图5～图7可知：在降雨渗透作用下，同样计算步数时，顺缓层理边坡楔形滑移的态势更加明显，最大位移出现在坡脚处，约为319 mm，相较于无水力学作用时增长了135%，坡底也出现了隆起现象，这是由于滑移体挤压坡底岩体造成的；边坡沿滑移面滑移产生的最大剪切位移达到280 mm，且随着坡脚剪出、滑移体后缘拉裂，坡体内的楔形滑移轮廓更加明显，降雨渗透的水力学作用降低了顺缓层理边坡的稳定性，加剧了边坡滑坡的趋势。

3.3 层理倾角对边坡稳定性的影响

为进一步分析层理倾角对节理化层状岩质边坡变形稳定性影响，不考虑降雨渗透作用，其他条件不变，改变层理倾角分别为 α=10°、30°、50°、70°、90°、110°、130°、150°、170°（α＞90°时为反倾岩质边坡）。节理化层状岩质边坡位移d随倾角α变化如图8所示。

由图8可知，对于顺层层理边坡（α=10°、30°、50°、70°），随着层理倾角的增大，最大位移量先增加后减小，呈现出两头低、中间高的钟型。α=50°时，位移量最大，达到170 mm。当α＞50°时，位移量陡然下降，这是由于层理倾角过大，边坡岩体沿着层理面滑移时受到边坡底部的阻碍；对于反倾边坡，同样存在最大位移量随倾角的增大先增大后减小的现象。总体来说，反倾岩质边坡的位移量要大于顺层边坡，稳定性也更差。

图8 边坡位移随层理倾角的变化

图9 不同层理倾角边坡位移矢量图

不同层理倾角边坡位移矢量图如图9所示，观察图9可知，随着层理倾角的增大，顺缓层理边坡的破坏模式由滑移—拉裂过渡为滑移—弯曲，反倾边坡主要表现为拉剪破坏。

4 结论

利用UDEC软件，模拟分析了不同条件下节理化岩质边坡的变形效应及稳定性，得到以下主要结论：

（1）边坡岩体结构对边坡滑移变形的控制作用显著，顺缓层理边坡稳定性明显低于水平层理边坡，降雨渗透的水力学作用加剧了顺缓层理边坡滑坡的趋势，工程中应加强对坡脚的加固处理。

（2）一般情况下，边坡位移随层理倾角的增加先增大后减小，反倾边坡的稳定性低于顺层边坡，更易失稳。

（3）随着层理倾角的增大，顺缓层理边坡的破坏模式由滑移—拉裂过渡为滑移—弯曲，反倾边坡主要表现为拉剪破坏。