船舶艉轴承间隙对轴系回旋振动特性影响分析

田川， 杜敬涛， 许得水， 李文龙

(哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)

船舶推进轴系的回旋振动实质上是转轴的进动，其振动特性受影响的因素较多。除了轴系本身结构对其影响外，轴承支点位置、轴系校中状态、支承系统特性等也对其有较大影响[1]。艉轴是船舶轴系中的最后一段，由于它的悬伸布置以及螺旋桨具有较大的自重，使得对艉轴起支承作用的艉轴承成为船舶轴系中负荷最大的轴承。由于轴系运转的不稳定性，导致轴承润滑状态不良，影响了液膜的支承刚度，最终使得支承系统总体刚度受影响[2]。因此，艉轴承的动态特性对轴系回旋振动的影响就显得至关重要。

目前研究人员对油膜动态特性分析已经做了大量的工作[3-7]。魏维等[8]研究了轴承设计间隙对最小油膜厚度、油膜压力分布、动态特性系数以及失稳转速的影响，但得到的规律只具有一般性，对特定的轴承，设计间隙对动态特性系数的影响是复杂的，不是一个简单的曲线可以表达的。王磊等[9]借助有限元软件，分析了螺旋桨惯性力矩(陀螺力矩、应力刚化效应和旋转软化效应等)对轴系回旋振动的影响，对轴承进行了简化处理，但没有考虑轴承对轴系回旋振动的影响。李小军等[10]利用ANSYS软件，分析船舶推进轴系后艉轴承刚度各向同性和各向异性时对轴系回旋振动的影响，但没有具体分析轴承的刚度变化，依然是将轴承简化成一个刚度不变的弹簧支承。夏极等[11]分析了油膜动态特性系数各向同性和异性时对轴系回旋振动特性的影响，但他没有考虑轴承的设计间隙对轴系回旋振动的影响。现存对轴系回旋振动特性的研究，是将轴承简化为弹性支承，其等效的支承刚度是固定不变的，而实际工况下轴承刚度是随转速动态变化的，对轴系的回旋振动有较大影响。目前轴承设计没有考虑轴承刚度变化的影响，未充分研究轴承动态刚度对轴系临界转速影响的机理。

因此本文以船舶艉轴承为研究对象，建立轴承流体润滑的数学模型，根据载荷增量法得到轴承的液膜刚度，研究了艉轴承的设计间隙对液膜刚度的影响；在此研究基础上，利用ANSYS建立船舶推进轴系模型，考虑轴承的刚度变化，计算轴系回旋振动的临界转速，分析艉轴承不同设计间隙对轴系回旋振动的影响。

1 分析模型

1.1 推进轴系模型

船舶推进轴系由齿轮箱、推力轴、中间轴、螺旋桨轴和支承轴承及其附件组成，其一般结构布置形式如图1所示。

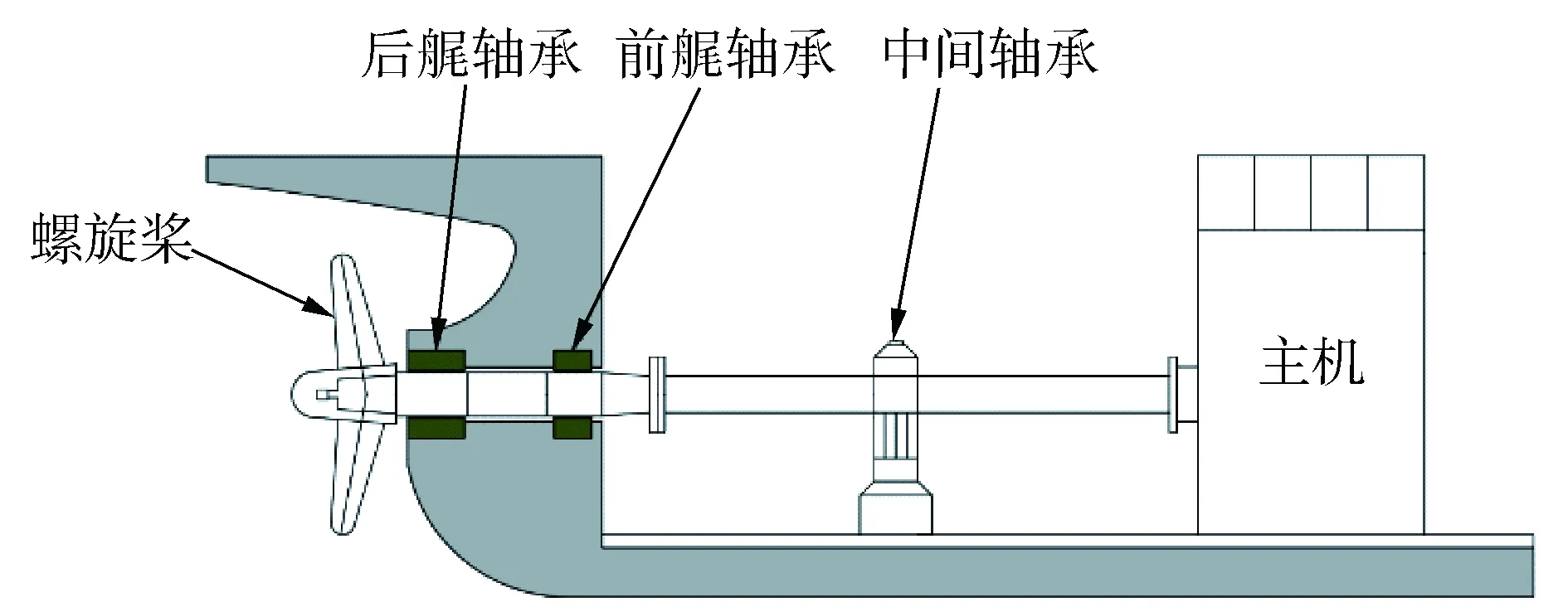
图1 船舶推进轴系结构示意Fig.1 Schematic diagram of ship propulsion shafting structure

本文选用某大型船舶推进轴系为研究对象，其推进轴系实体模型如图2 所示，额定转速为150 r/min，轴系全长13.55 m，螺旋桨叶片数为4，轴承支承数为3。以等截面均质轴端的形式建立螺旋桨轴、中间轴，用梁单元来代替；对于螺旋桨，用质量单元来代替；轴承简化成弹簧支承，用弹簧单元代替；法兰看为均质刚性圆盘组件。边界条件：对于回振，首段元件为高弹性联轴器，取为自由端，艉端边界条件，即螺旋桨处，取为自由端。离散后得到如图3所示的推进轴系简化模型，主要参数如表1所示。

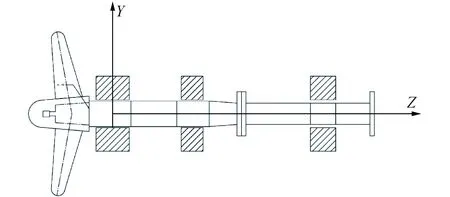
图2 推进轴系实体模型Fig.2 Propulsion shafting solid model

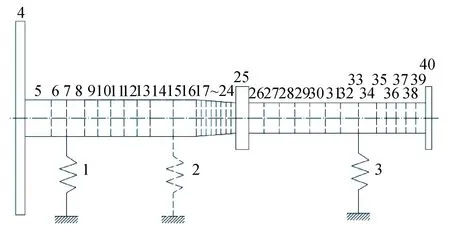
图3 推进轴系简化离散模型Fig.3 Propulsion shafting simplified discrete model

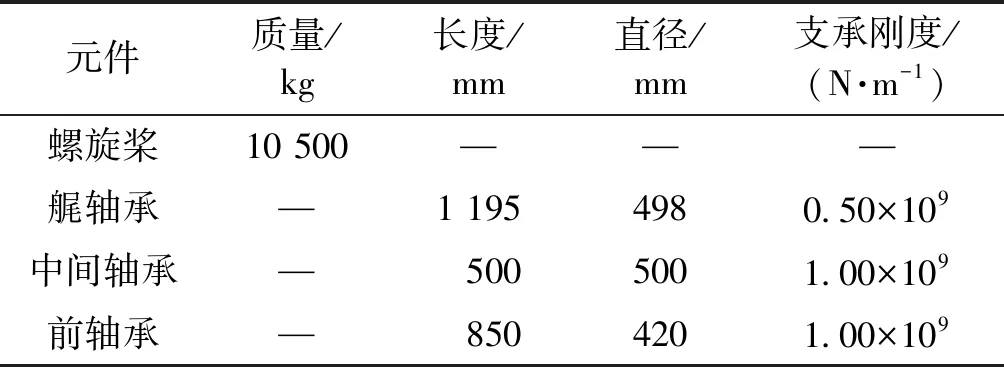
表1 轴系几何参数Table 1 Shaft geometry parameter

1.2 艉轴承模型

从船舶推进轴系的实体模型中提取出艉轴承，如图4所示，规定x方向为水平方向，y方向为竖直方向，O为轴承衬中心，O0为轴颈平衡位置中心，h为M点处的液膜厚度，r为轴颈半径，R为轴承衬半径，φ0为偏位角，e为偏心距。

图4 艉轴承模型周向坐标Fig.4 Tail bearing model circumferential coordinate

2 轴承液膜刚度推导

液膜刚度与许多因素有关，例如轴承结构、负载大小、润滑剂的粘度、温度、轴承间隙等。它还与转速密切相关，它的计算由不稳定载荷下Reynold方程推导求得，在近似计算时，Jasper建议：k=CP/δ，P轴承静负载；C轴承径向间隙；δ系数，Jasper建议取2。对于50 000 t以下的运输商船，艉管后轴承支承刚度约在0.5～2.0×109N/m范围内[1]。本章由流体动力润滑理论建立艉轴承的数学模型进行刚度计算。

2.1 Reynolds方程

径向滑动轴承的Reynolds方程为：

(1)

式中：h为润滑剂膜厚度；p为润滑剂膜压力；η为润滑剂动力粘度；U为轴颈圆周线速度，其中U=ωr=2πNr，ω为轴颈角速度，N为轴颈转速；x表示周向坐标，y表示径向坐标，z表示轴向坐标。

对Reynolds方程，式(1)进行无量纲化。

轴承宽z的无量纲形式为：z=λ(L/2)⟹λ=z/(L/2)，其中-1≤λ≤1；

轴承圆周方向x的无量纲形式为：x=φr⟹φ=x/r，其中0≤φ≤2π；

油膜压力p的无量纲形式为：p=Pp0⟹P=P/p0，其中P0=6Uηr/Cr2；

任意截面z的油膜厚度无量纲形式为：Hz=hz/Cr=1+εcosφ，式中，Cr为轴承径向间隙；ε为偏心率，ε=ez/Cr。

将上述各参数的无量纲形式代入式(1)，可得二维雷诺方程无量纲形式为：

(2)

式中：d为轴颈直径；L为轴承宽度；φ、λ为无量纲坐标；P为无量纲液膜压力；H为无量纲液膜厚度。

本文选用Reynolds边界条件，该边界条件认为液膜呈不连续分布，液膜的自然破裂现象形成液膜压力终止点，即在经过最小液膜厚度后的某一角度φ2处液膜自然破裂，则φ2处为液膜压力终止点。无量纲化后，边界条件可表示为：

(3)

应用Reynolds边界条件积分求解可得到液膜压力分布P(φ、λ)，本文利用FDM法对Reynolds方程近似求解，最终得到如图5所示的液膜压力分布图，本文计算得到的无量纲最大液膜压力为Pmax=5.730 6，文献[7]的结果为5.662 1，基本吻合。

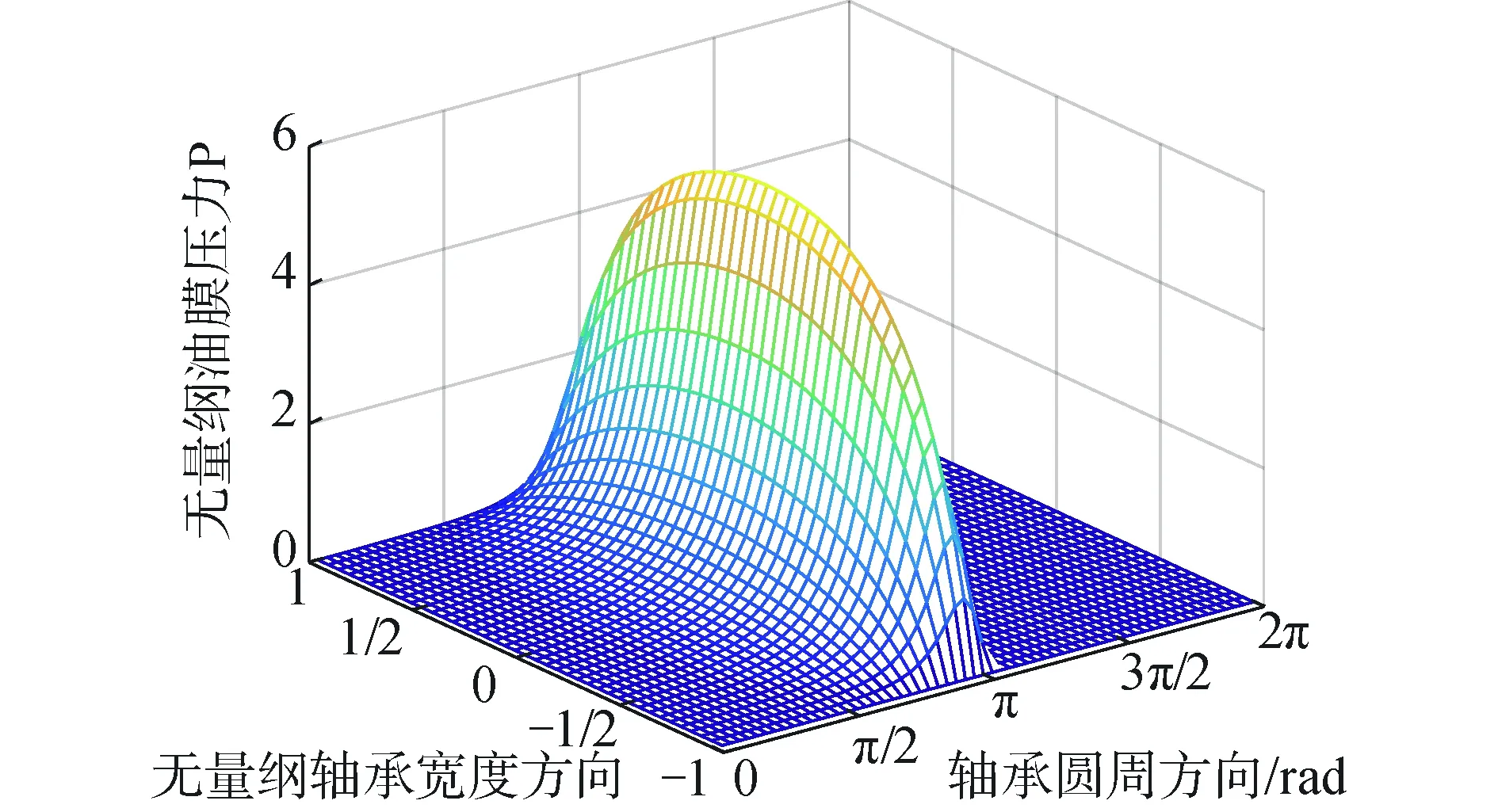
图5 无量纲液膜压力分布云图Fig.5 Dimensional liquid film pressure distribution cloud map

2.2 轴承液膜刚度求解

在获取液膜压力后，通过积分可求得液膜承载力，再将各参数代入无量纲表达式，可得到水平分力Fx和垂直分力Fy为：

(4)

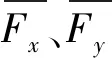
(5)

最后通过载荷增量法求取液膜刚度，当轴颈在水平方向上发生位移扰动Δx时，根据几何关系可得扰动后的偏心距和偏位角计算公式为：

(6)

(7)

当轴颈在水平方向上发生位移扰动Δy时，根据几何关系可得扰动后的偏心距和偏位角计算公式为：

(8)

则：

(9)

按图6所示的流程图进行Matlab编程，即可建立轴承支承刚度的数学分析模型。试算轴承模型参数如下：轴承长度0.2 m，轴承直径0.1 m，轴承间隙0.3 mm，润滑剂粘度0.02 Pa·s，轴承负载1 kN。本文计算得到的轴承液膜刚度与文献[7]的结果对比如图7所示，2个结果基本吻合，验证模型正确，可进行下步研究。

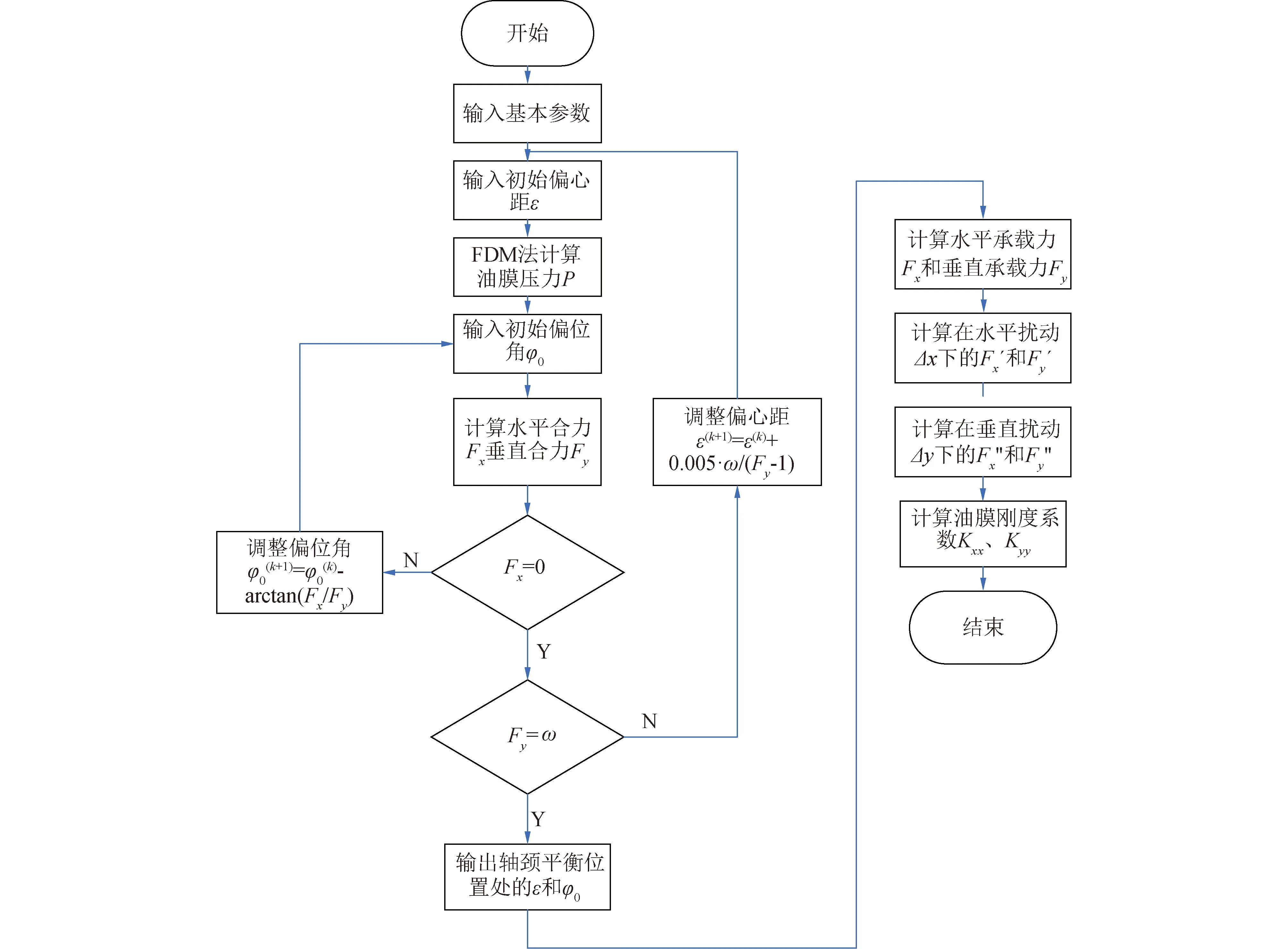
图6 Matlab流程图Fig.6 Matlab flow chart

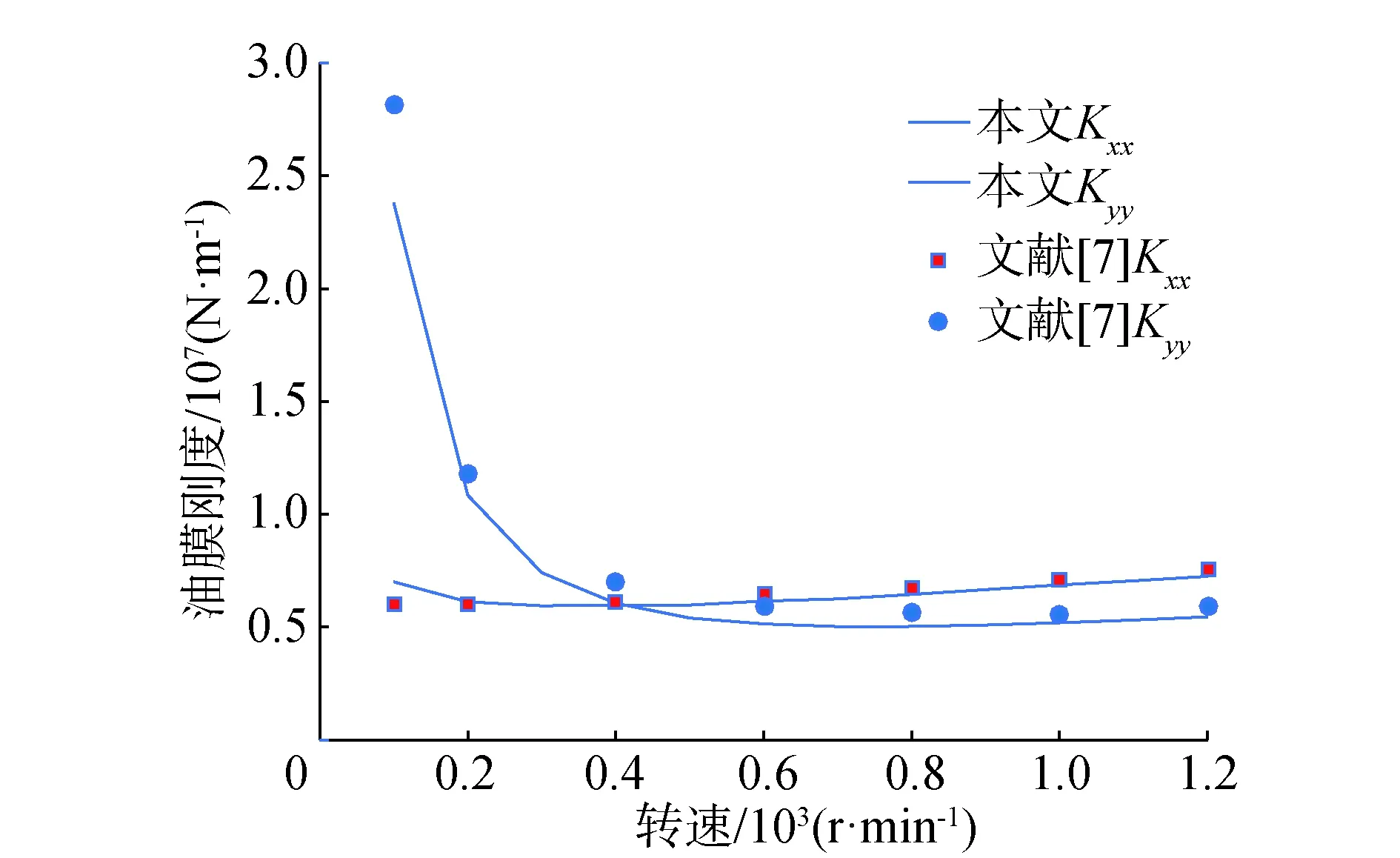
图7 试算轴承液膜刚度与文献结果对比Fig.7 Trial calculation of bearing liquid film stiffness and literature comparison results

3 结果分析

3.1 临界转速

由于螺旋桨的附连水效应，需要考虑螺旋桨附连水质量，本文取质量附连水系数为1.15，最后螺旋桨的附连水质量为12 075 kg，同样考虑极转动惯量附连水系数和径向转动惯量附连水系数后，得到螺旋桨附连水极转动惯量和径向转动惯量分别为16 861 kg·m2、10 376 kg·m2。艉轴承支承点距轴承衬后端面的距离为轴承衬长度的1/5，其余轴承支承点位置取轴承衬中央。

采用MASS21单元模拟螺旋桨，MASS21成为结构质量单元，每个节点可多达6个自由度，每个坐标轴方向可以有不同的质量和转动惯量。使用COMBIN214单元模拟轴承，该单元可考虑更多的轴承特性，如2个支承方向的交叉项、随转速的变刚度和变阻尼特性等。使用BEAM188单元模拟轴，改变截面大小模拟变截面轴段、联轴器、法兰等部件。轴承的平面位于XY平面，推进轴位于Z方向上，材料的弹性模量为2.1×1011N/m2，泊松比为0.3，密度为7 800 kg/m3。

建立推进轴系的有限元计算模型如图8所示，共包含133个节点，129个梁单元，3个轴承单元，1个质量单元，7个截面和1个变截面。

图8 推进轴系有限元模型Fig.8 Propulsion shafting finite element model

为避免扭转振动和纵向振动对回振结果产生影响，需要约束有限元模型轴向方向的平动位移和转动位移，弹簧接地节点约束全部位移。对推进轴系加载约束条件，进行模态求解。

传递矩阵法是将各个元件断面(点)在振动时的特性用状态矢量位移幅值y、角位移幅值θ、力矩M、剪力Q表示出来，再由各类元件的传递矩阵将轴系首末两端状态联系起来，因为首末两端状态已知，方程即可求解，具体方法可参见文献[1]。

求解轴系的临界转速，与文献[12]和传递矩阵法求解的结果对比如表2所示，发现临界转速误差均在允许范围内，最大误差也没有超过1%，说明此轴系的ANSYS模型满足要求，可以进行后面的求解。

3.2 轴承设计间隙对液膜刚度的影响

利用Matlab编程，建立艉轴承液膜刚度分析的数学模型，艉轴承相关参数如表3所示。

表3 艉轴承相关参数Table 3 Tail bearing related parameters

分别选取间隙为0.3、0.35、0.4、0.45、0.5 mm；螺旋桨质量为10 500 kg，轴的总质量为6 537.5 kg，3轴承总负载为166 967.5 N，由于螺旋桨悬挂式布局方式，艉轴承承受负载较大，参考文献[13]，取艉轴承承受1.5倍率负载，即艉轴承静负载为83 483 N；选取转速20～1 200 r/min进行分析。计算艉轴承的液膜刚度，得到如图9～12所示的刚度变化曲线图。

由图9～12可发现，Kxx和Kyy在低速区会出现波动，随着转速N的增加，波动会慢慢减小，并逐渐趋于平稳状态。随着轴承设计间隙Cr的增加，Kxx和Kyy出现波动时的转速区会逐渐加大，即出现波动时的转速会增大，例如当Cr=0.3 mm时，波动首先在94～97 r/min出现，当Cr=0.35 mm时，波动首先在128～132 r/min出现，直到Cr=0.5 mm时，波动首先在260～279 r/min出现。Kxx随Cr的增加而递减，而Kyy随Cr的增加，刚开始递增，当转速升高，又会慢慢演变成递减。

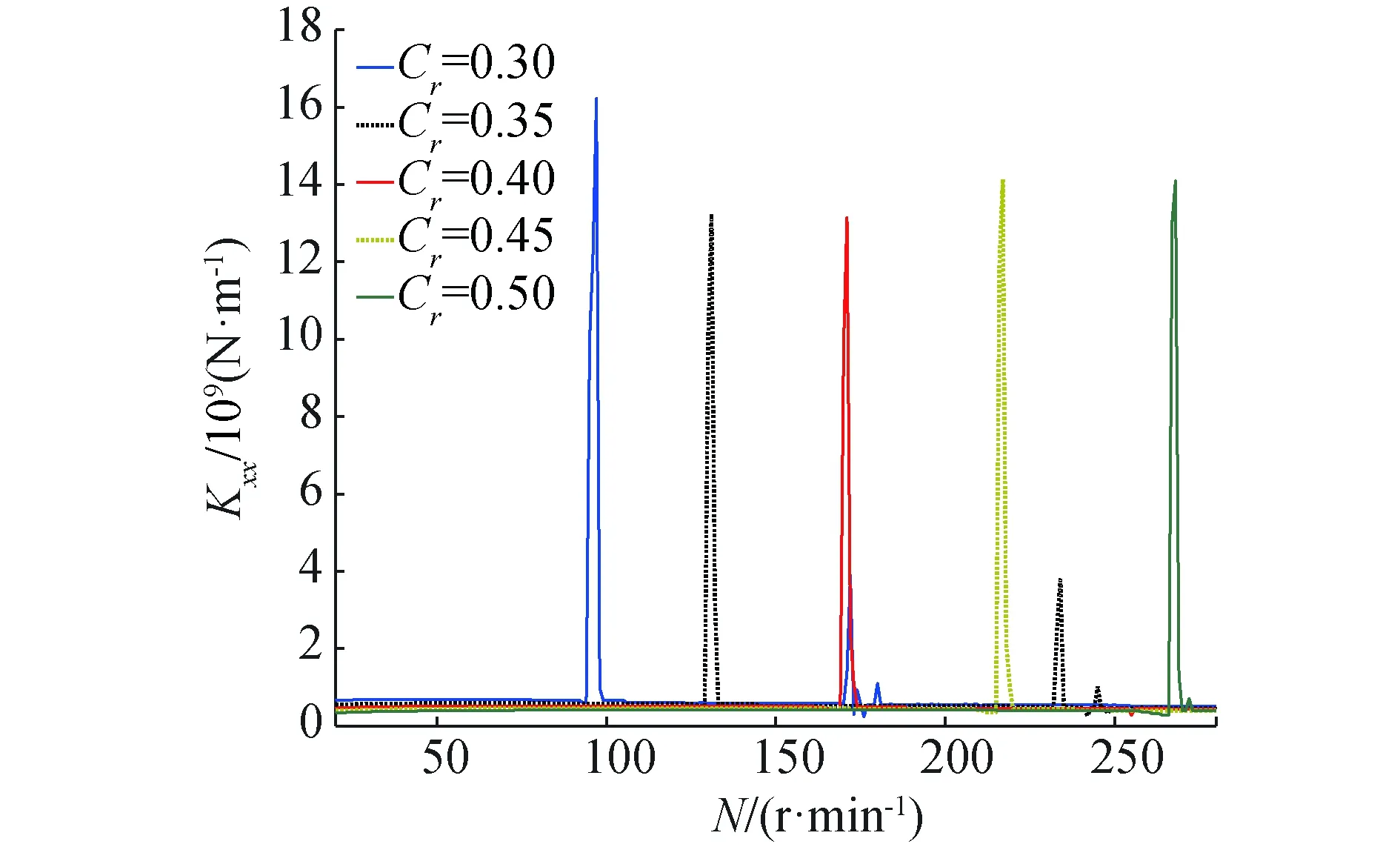
图9 Kxx低速区间Fig.9 Kxx low speed interval

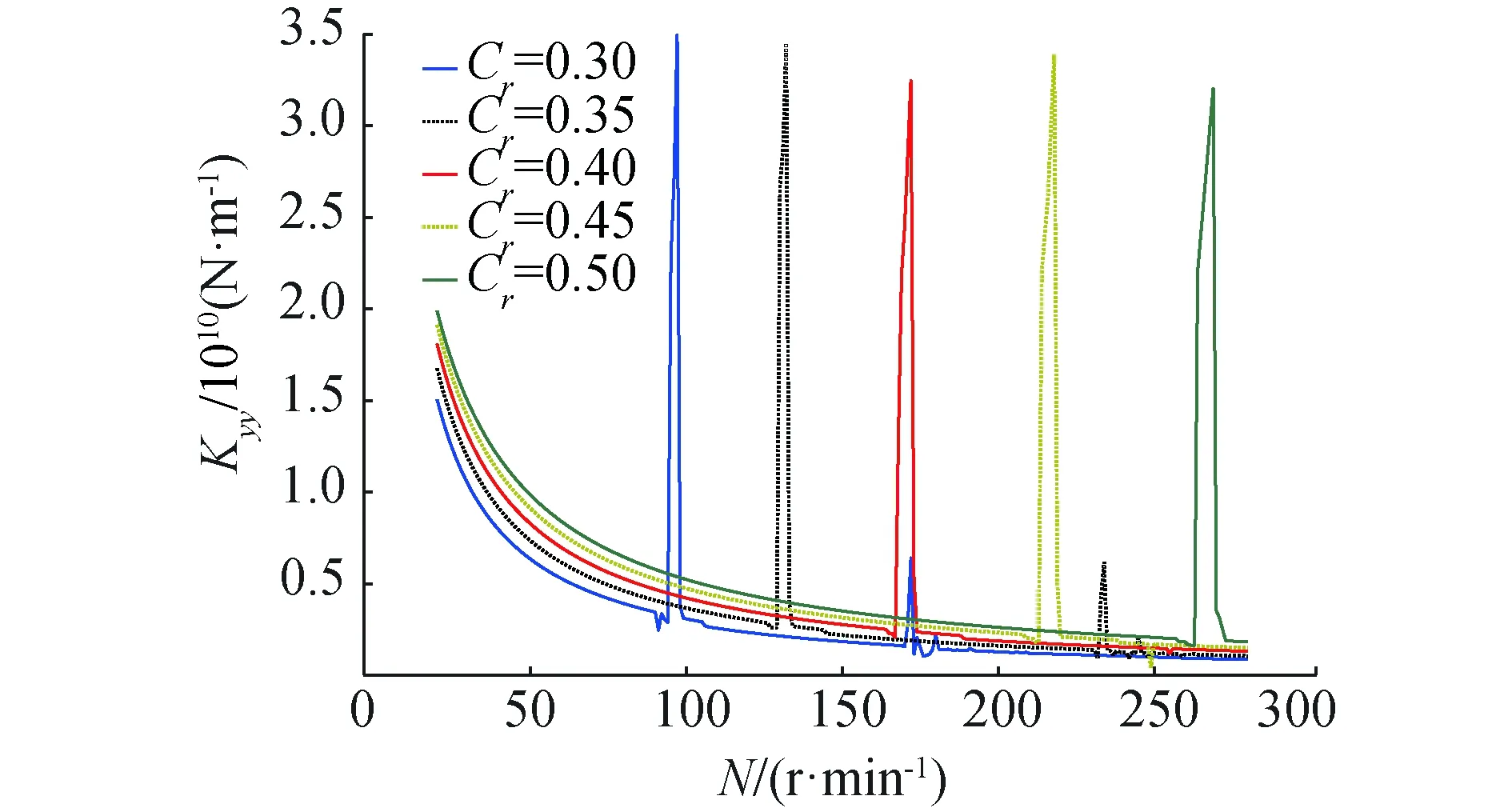
图10 Kyy低速区间Fig.10 Kyy low speed interval

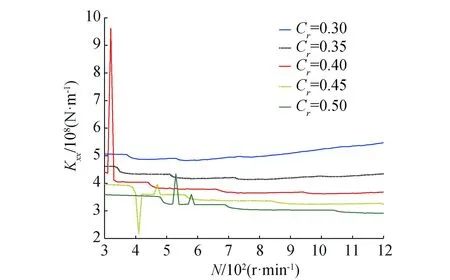
图11 Kxx高速区间Fig.11 Kxx high speed interval

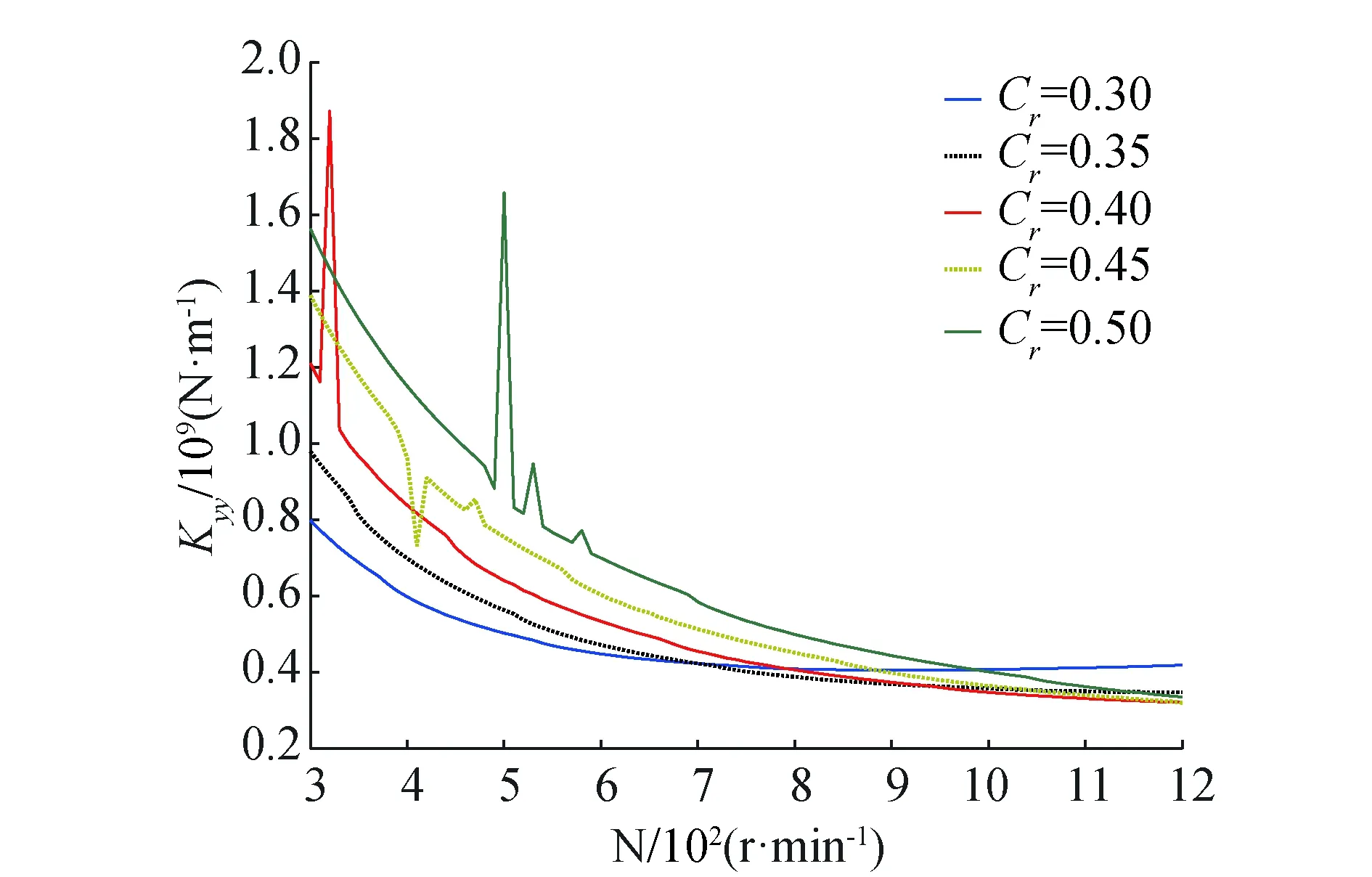
图12 Kyy高速区间Fig.12 Kyy high speed interval

3.3 刚度变化对轴系回振的影响分析

由上一节的结果可以看出，轴承刚度随转速呈非线性变化，会出现波动，并且Kxx和Kyy随轴承设计间隙的变化规律也很复杂。因此，艉轴承设计间隙对轴系回旋振动造成的影响就有待进一步的研究。将上一节得到的轴承随间隙Cr变化的十组刚度导入到ANSYS软件中进行轴系回旋振动临界转速的求解，得到表4所示的临界转速结果。

固有频率与临界转速之间的关系为：ωn=Zp·ω(r/min)，其中ωn固有频率，ω为临界转速，Zp为螺旋桨叶片数。得到如图13和图14所示的轴系固有频率随艉轴承间隙变化图。

由表4可以发现，当艉轴承刚度取流体动力润滑理论计算的结果时，轴系的临界转速在表2中的数值附近变化，验证了轴承模型的正确性。随着艉轴承设计间隙的增大，轴系临界转速总体上是呈减小趋势，但在Cr=0.45 mm时，轴系的叶片次临界转速出现增长，这是因为当Cr=0.45 mm时，刚度在转速N为216～220 r/min时出现较大的波动，临界转速正好处于此区间内，导致叶片次临界转速增大。由此可见，刚度出现波动的转速区域对轴系回振的影响较大。从图13和图14可以看出，正回旋的一次和逆回旋的倍叶片次固有频率变化比较大。

表4 不同间隙的临界转速Table 4 Critical speed of different clearances r/min

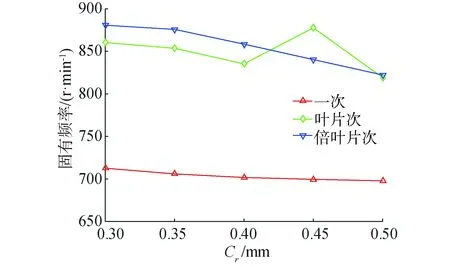
图13 一阶逆回旋固有频率Fig.13 First-order inverse lateral natural frequency

为验证刚度波动对轴系回旋振动的影响，说明图13中轴系叶片次临界转速出现增长变化的现象不是唯一的，另取轴承设计间隙为Cr=0.32 mm和Cr=0.465 mm，分别计算在转速20～1 200 r/min下的水平方向和垂直方向的刚度值。当Cr=0.32 mm时，Kxx和Kyy方向的刚度值在转速107～111 r/min出现波动；当Cr=0.465 mm时，在转速226～234 r/min出现波动。再进行回旋振动特性分析发现，当Cr=0.32 mm时，轴系的逆回旋倍叶片次临界转速相对于表4中的Cr=0.3 mm和Cr=0.35 mm时增大，为111.69 r/min，因转速区间在额定转速以内，此时轴系出现共振，不可忽略。当Cr=0.465 mm时，轴系的逆回旋叶片次临界转速相对于Cr=0.45 mm和Cr=0.5 mm时增大，为280.02 r/min。因此，艉轴承的刚度在某个转速区内出现的波动确实会对整个轴系的回旋振动产生不可忽略的影响。轴承设计时应充分考虑额定转速以内出现的刚度波动现象，以及对临界转速造成的变化，避免共振。

图14 一阶正回旋固有频率Fig.14 First-order positive Lateral natural frequency

4 结论

1)轴承水平方向刚度随轴承设计间隙增大而递增，垂直方向的刚度随间隙增大先减小再渐变为递增。刚度随轴颈转速出现波动，但随着转速的升高会逐渐收敛。刚度会在特定转速区间内会出现波动，当间隙变大时区间对应的转速随之增大。

2)轴系回振的频率随着间隙的增加而递减，且对正回旋的一次固有频率的影响较大，在间隙为0.45 mm时，轴系逆回旋的叶片次临界转速出现增长变化，这是由于在这个转速区间油膜刚度出现较大波动。因此，油膜刚度的波动变化对轴系回振的影响不容忽略。

3)临界转速增长变化的现象不是唯一的，轴承间隙设计时应尽量取允许范围内的最大值，这样可以避免在轴系额定转速范围内出现轴承液膜刚度的波动及轴系的共振现象。