限制水域船舶水动力干扰快速计算方法

黄金， 邓强， 许辰， 诸葛凌波， 任慧龙， 周学谦

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 15001； 2.教育部船舶与海洋工程技术国际联合合作实验室，黑龙江 哈尔滨 150001； 3.中国船舶及海洋工程设计研究院，上海 200001)

船舶在港口、航道等拥挤水域内的自主航行，作为船舶智能航行中的难点问题，吸引了国内外学者的广泛关注。大船型船舶由于其尺寸与载重量极大，其受到的水动力在船舶操纵过程中往往是不可忽略的。当船舶在港口、码头以及内河中航行时，由于空间限制，船舶常常会以较小的距离实现赶超与会遇，而在此操纵过程中船舶受到的水动力干扰极大，并严重威胁船舶航行安全。因此，研究限制水船舶水动力干扰的实时预报方法可为船舶航行安全与自动航行提供一定的技术支持。

船-船水动力干扰作为船舶水动力干扰问题的主要内容之一，其主要的研究方法主要分为2种：模型试验与数值模拟，后者根据计算原理，可分为粘性流方法与势流方法。基于模型试验的方法更能准确可靠地预报实船的水动力性能，因此国外学者很早就对浅水中的船-船水动力干扰进行了模型试验研究。Dand[1]采用模型试验的方法模拟浅水中两船相遇与赶超中的船舶水动力干扰，并研究了航速、船-船横向距离与水深对干扰力和船体浮态(升沉、纵倾)的影响。Vantorre等[2]对4个不同的船模展开了全面的模型试验，并使用回归分析的方法建立了能够预测浅水中水动力干扰力极值的数学模型。

数值模拟方面，根据考虑因素的不同，浅水中的船舶水动力干扰的研究方法主要可以分为3类：

1)模拟真实流体流动的粘性流方法；

2)忽略粘性效应的势流方法；

3)忽略线性效应与自由液面效应的势流方法。

粘性流方法主要是基于雷诺平均N-S方程(RANSE)求解船体周围的流场的特征，该方法能够考虑自由液面的变化与流体的粘性效应，故其计算精度高。刘晓艳[3]使用CFD软件Fluent，计算了限制水域内两船会遇与追越过程中的船舶间水动力干扰，研究了湍流模型与时间步长对计算结果的影响。高智勇等[4]基于RANS方程研究近距并行两船的相互干扰效应对船舶操纵性的影响。Pawar等[5]采用三维粘流方法探究了不同航道情况下航行船经过系泊船的影响。Fonfach等[6]利用不同的流动模型，研究了粘性与自由液面效应对船舶间水动力干扰的影响，对比结果显示：粘性对干扰力的影响较小，但当两船横向距离非常小时，自由液面的影响是较大的。粘性流方法存在低计算效率的特点，不能用于水动力干扰的实时预报，但相较于其他数值方法，粘性流模拟最能够反映真实的流场特性，可用于验证其他计算方法的可行性。

由于粘性效应在船-船水动力干扰中的影响较小，忽略粘性效应的势流方法也被广泛应用于船舶水动力干扰的研究工作中。Söding等[7]使用Rankine源法分析了发生在欧洲Elbe River内一起真实的船舶碰撞事故。王隶加[8]应用泰勒展开边界元法和频域格林函数，系统研究了浅水中两船并行航行时相遇和超越情况下干扰力和干扰力矩的问题。Yuan[9]使用计及自由液面变化的三维边界元法，分别计算了限制水域内船舶沿岸壁行驶、船舶进入船闸及两船相遇过程中的水动力干扰力，对比粘性流结果与势流结果显示：即使没有考虑粘性作用，势流方法仍能获得较高精度的数值结果。但该方法的计算效率较低，求解一个时间步大概需要几分钟的时间，远远不满足实时计算的要求。

由于港口、航道等限制水域内的波浪较小，又因为限制水域内的航速限制，船舶运动引起的兴波较小，不计自由液面效应的势流理论方法也可用于预报限制水域的船舶水动力干扰问题。Sutulo等[10]使用Hess & Smith面元法[11]求解深水中的船舶水动力干扰问题，由于基于低傅汝德数假设，使用了合模方法[12]处理自由液面条件，该算法的计算效率极快。徐华福[13]基于同样的假设，使用高阶面元法研究了水深、船船横向距离与船速对浅水中的船舶水动力干扰的影响。相较于常值面元法，高阶面元法具有更高的鲁棒性，但其计算效率仍不满足实时计算的要求，采用类似高阶面元的研究还有王隶加[8]。Xu 等[14]研究了基于势流理论的水动力干扰预报方法中不对称网格的误差特性。Huang 等[15]基于势流理论提出了一个船岸干扰水动力预报方法，与实验结果和基于RANSE的粘性数值模拟结果相比，除水深吃水比极小的工况外，基于势流理论的数值计算精度均在可接受范围内。

由上述文献可知，使用合模方法模拟自由液面是一种十分高效的方法。并且在文献[10]可以看到，基于常值面元法与高阶面元法获得的横向力与转首力矩差异很小。因此，本文采用常值面元法实时预报限制水域内的船舶水动力干扰。使用镜像法处理水平水底处的边界条件，基于低傅汝德数假设，使用合模方法模拟自由液面。分别模拟船舶经过无航速船舶与两船相遇过程中的船舶水动力干扰，通过与试验结果对比，验证数值算法的可行性与适用性，确定所用假设的合理性。

1 船舶水动力干扰实时计算方法

1.1 坐标系定义

如图1所示，对于限制水域内的两船之间的水动力干扰问题，建立O-ξηζ，o1-x1y1z1和o2-x2y2z23个坐标系。其中，大地坐标系O-ξηζ的ξOη平面与静水面重合，ζ轴竖直向下。o1-x1y1z1和o2-x2y2z2分别与Model 1和Model 2固连，x轴指向船艏，y轴指向船体右舷，z轴方向与ζ轴相同。

图1 坐标系定义Fig.1 Definition of coordinate systems

1.2 控制方程与边界条件

本文基于流体不可压缩，无粘性，流动无旋的理想流体假设，采用势流理论实时求解浅水中两船赶超与相遇过程中的水动力干扰问题。流域内合速度势Φ(ξ,η,ζ,t)可表示为：

Φ=Vcurξξ+Vcurηη+φ

(1)

式中：Vcurξ和Vcurη分别是水中水平均匀流Vcur的纵向与横向分量。φ(ξ,η,ζ,t)为诱导速度势，诱导速度势的梯度为诱导速度VI=φ。在任意时刻，流域中任意一点的诱导速度势均满足拉普拉斯方程：

Δφ=0

(2)

诱导速度势φ在船体湿表面上满足不可穿透条件：

(3)

式中：n是船体湿表面上单位外法向量;Vr是局部相对速度：Vr=Vi-Vcur;Vi是第i条船的速度。在水平水底上，速度势φ同样满足不可穿透边界条件：

(4)

基于低傅汝德数假设，忽略船体兴波对船舶水动力干扰的贡献，使用合模法简化自由液面处的边界条件：

(5)

势流理论中，流域内任意一点某物理量的值可由边界上的值表示，边界元积分方程为：

(6)

式中:S是2条船的湿表面;σ为源强;M(x,y,z)和P(x′,y′,z′)分别为场点和源点;f(M)=Vr(M)·n(M);G为格林函数。由于使用镜像法和合模模型分别处理水平水底与自由液面处的边界条件，如图2所示，本文使用镜像格林函数：

(7)

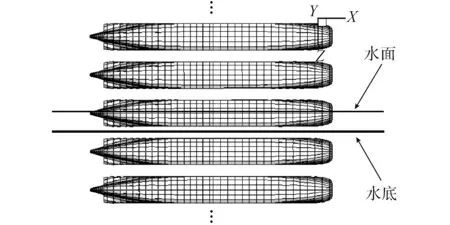
图2 镜像法示意Fig.2 The diagram of mirror image technique

1.3 数值求解

用Hess & Smith面元法将船体表面分割成N个四边形网格，上述积分方程(7)转化分线性方程组：

(8)

式中：Aij为影响系数矩阵，未知数σj为每个面元控制点处的源强。本文使用高斯-赛德尔迭代法求解该线性方程组的近似值。场点M处的诱导速度势φ与诱导速度VI可分别表示为：

(9)

(10)

船体表面压力分布由非定常伯努利方程可得：

(11)

式中：ρ是流体密度，VP=VI-Vr。通过沿着船体湿表面对压力p进行积分，可获得作用在第k条船的总干扰力：

(12)

1.4 船舶操纵与船间干扰力求解

根据船舶操纵性方程得到惯性项水动力：

(13)

(14)

对于本文所研究的问题，船体各方向的加速度都为零，式(13)获得的干扰力即为由船-船水动力干扰力。

2 计算参数与结果分析

分别模拟浅水中船舶平行赶超另一无航速船与两船平行会遇2种典型情况下的船-船水动力干扰问题。在模拟过程中，忽略水动力干扰对船舶姿态、轨迹与速度的影响。通过对比实验结果，验证实时计算方法的可行性与计算精度。

2.1 计算模型

以Dand[1]公开发表的实验报告中的货船与油船作为研究对象，两船的主要参数见表1，两船型线见图3、图4。

表1 船模参数表Table 1 Parameters of the models

图3 货船型线Fig.3 The body profile of cargo ship

图4 油船型线Fig.4 The body profiles of tanker

2.2 计算工况

本文从Dand[1]的报告中选取了5个实验工况，用于验证船舶水动力干扰实时计算方法。其中2个工况属于船舶赶超干扰，另外3个属于会遇问题。这5个工况的主要参数见表2和表3。

表2 赶超工况参数表Table 2 Configuration of the overtaking case

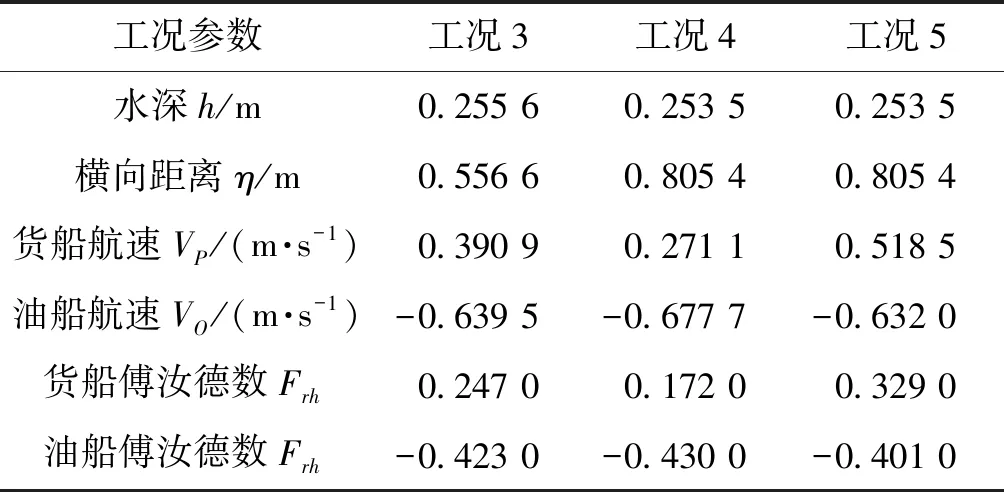
表3 会遇工况参数表Table 3 Configuration of the encounter case

2.3 计算参数的确定

面元数量和时间步长是影响计算结果的重要因素，为保证快速计算要求，并保证一定的精度要求，需要对计算参数进行确定。

面元数量和时间步长是影响船舶水动力干扰快速计算的重要因素。实时预报要求程序计算时间小于时间步长，而程序计算耗时主要在求解线性方程组，面元数量是最主要的因素。因此找出满足面元数量和计算时间的关系，就能确定不同面元数量对应的最小时间步长。通过多组数据得到如图5关系曲线。

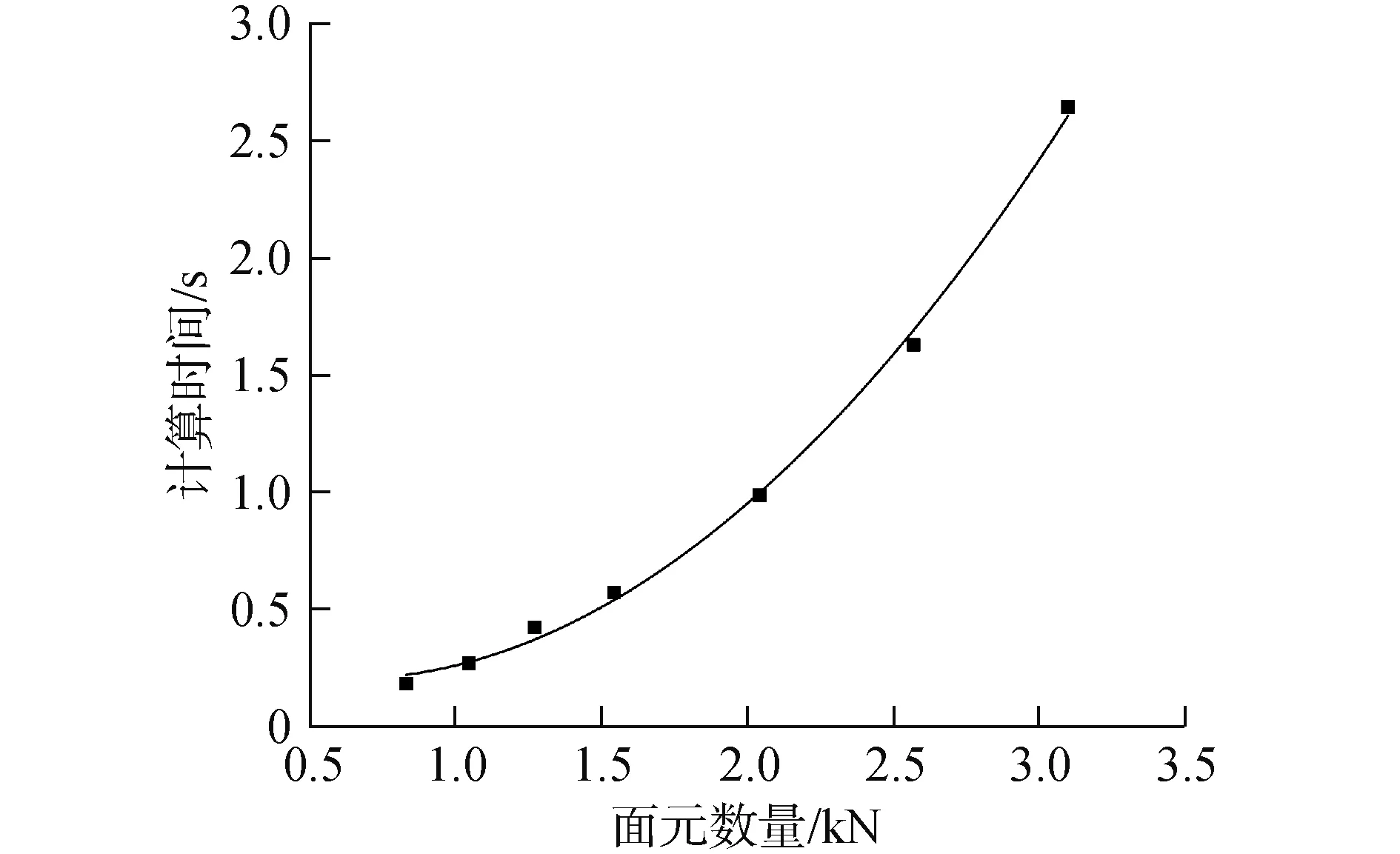
图5 面元数量与计算时间关系Fig.5 Number of panels versus calculation time

由图可得，本文船型计算时间与面元数量成二次曲线关系，经过最小二乘拟合得到如下关系式：t=0.349 07-4.74×10-4x+3.88×10-7x2。其中t为计算时间，x为面元数量。

由以上结果可得，为保证一定的精度要求，当面元数量较小时须采用较小时间步长，反之使用较大步长。因此，为了找到合适的面元数量和时间步长，对不同面元数量计算得到的干扰力进行计算并得到相对误差结果，满足误差最小的即为最佳面元数量，时间步长由上图确定。

选取面元数量为2 000，时间步长为0.5 s作为基准，由图5确定一系列不面元数量和时间步长，取不同工况计算干扰力结果并计算相对误差。相关参数见表4和表5，结果见图6和图7。

表4 面元数与时间步长表Table 4 Number of panels and time step

由图可得，误差最小出现在面元数量1 600附近，根据5%误差标准，面元数取1 520～1 680时，误差最小。取总面元数1 586进行计算，其中货船湿表面离散成798个面元，油船表面离散成788个面元，此时时间步长为0.5 s。两船的湿表面网格见图8、图9。

镜像次数n影响水平水底的建模精度，从而影响水动力干扰的预报精度。由图10可见，当镜像数n=7时，水动力干扰的预报结果趋于稳定，也验证了Suluto等[12]的结论。

表5 工况参数表Table 5 Configuration of the caculation case

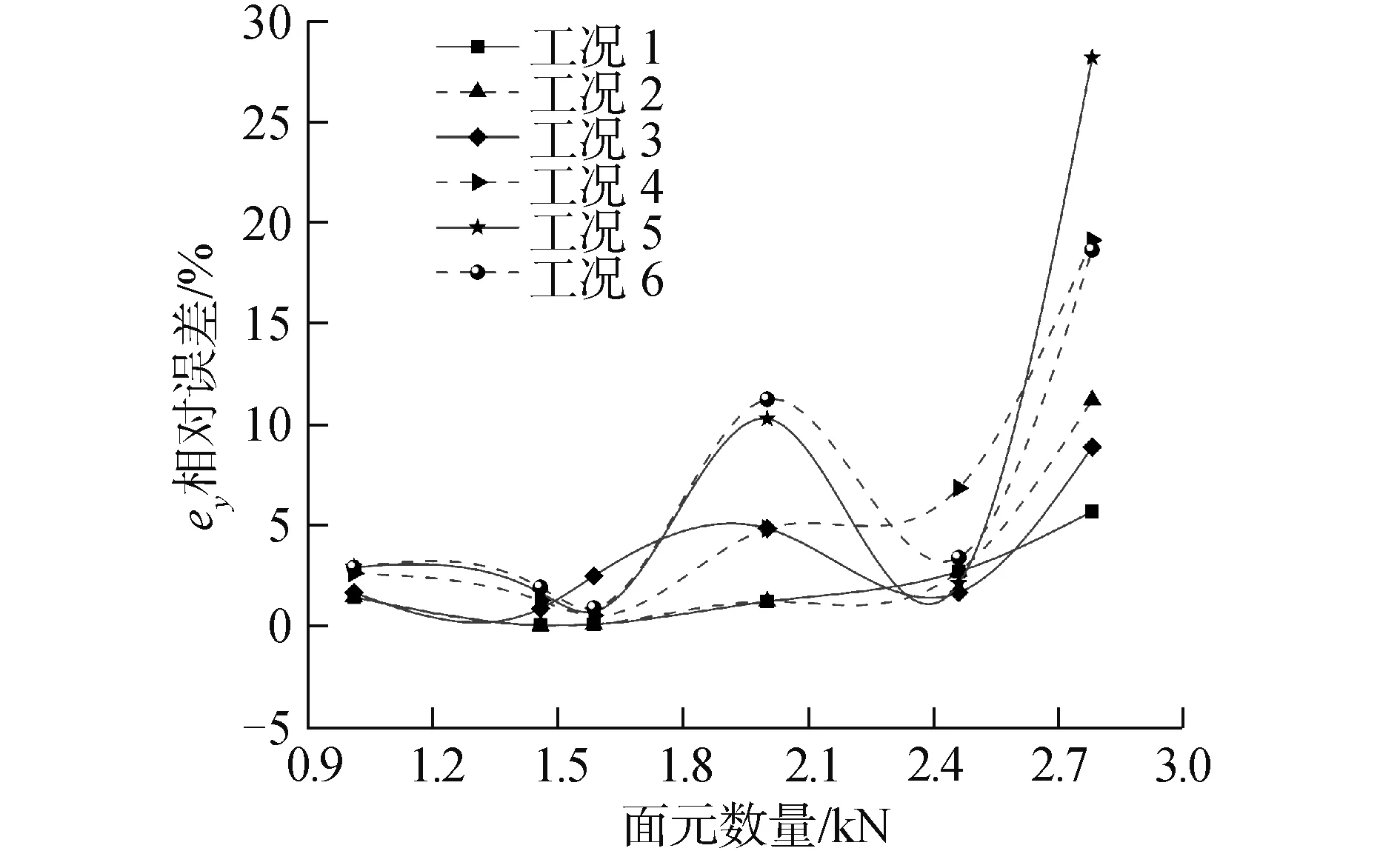
图6 横向力相对误差结果Fig.6 Relative error of sway force

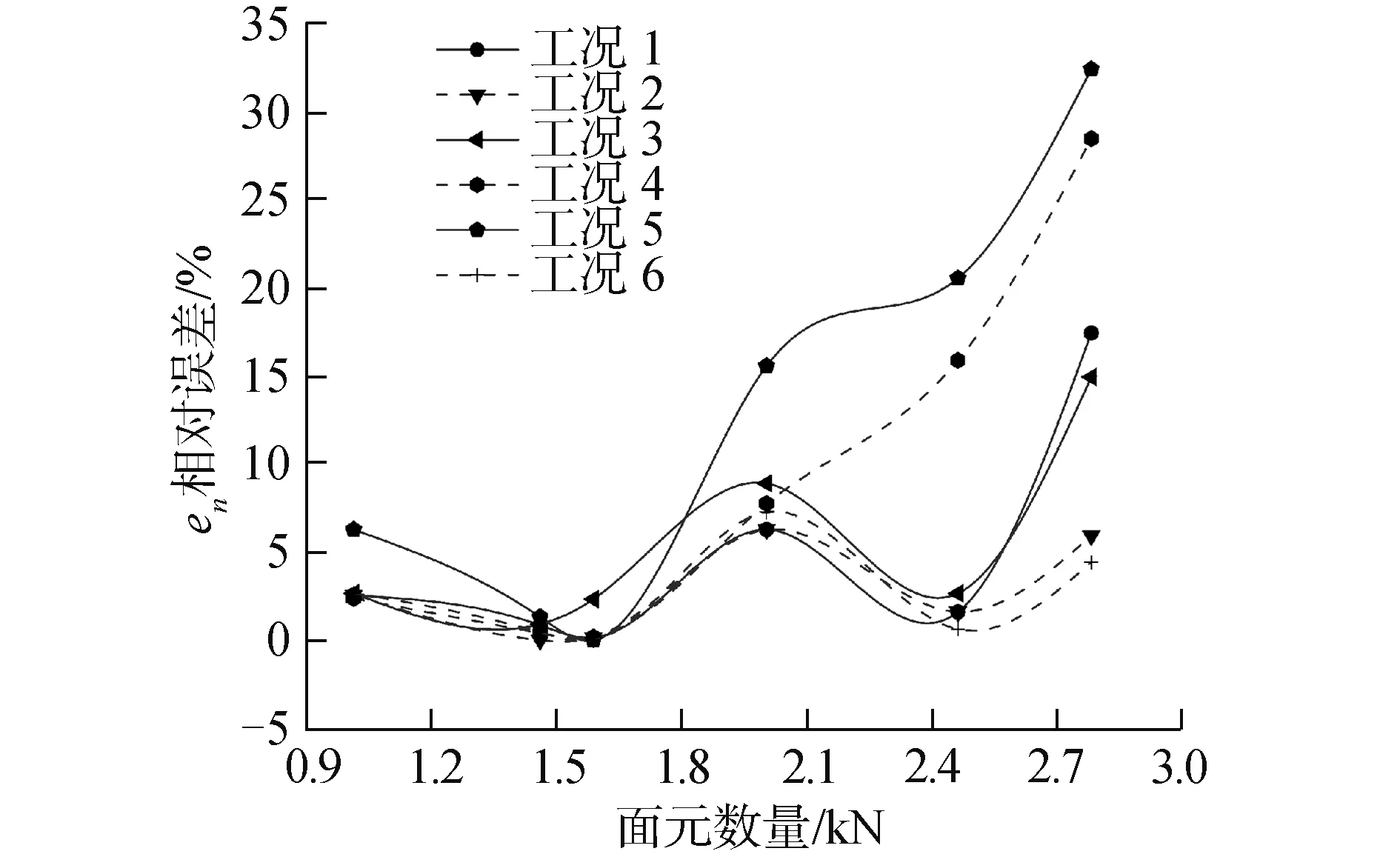
图7 摇艏力矩相对误差结果Fig.7 Relative error of yaw moment

图8 货船湿表面网格划分(面元数量818)Fig.8 Discretization of the wetted surface of the cargo ship

图9 油船湿表面网格划分(面元数量768)Fig.9 Discretization of the wetted surface of the tanker

2.4 数值结果与实验结果对比

由于Dand的实验报告中只有作用于油船干扰力的试验结果，因此本文只对作用于油船的干扰力进行对比。数值结果与试验结果都作无因次化处理：

(15)

式中：Cy和Cn分别是横向力与转艏力矩系数;B0和T0分别是货船的型宽与吃水。两船的相对位置也进行无因次化处理：

(16)

式中：ξp和ξo分别为货船与油船的纵向位置，L0为油船的垂线间长。当ξ<0时，两船的相对纵向间距逐渐变小。ξ=0时，两船船中对齐。ξ>0时，两船纵向间距逐渐变大。

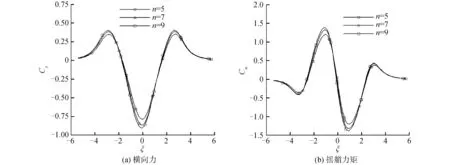
图10 不同镜像次数下油船受到的水动力干扰力Fig.10 The hydrodynamic interaction forces acting on the tanker obtained with different numbers of images

2.4.1 赶超工况

图11和图12是货船平行赶超无航速油船时，油船受到的船舶水动力干扰力，其中图11是工况1的模拟结果，图12是工况2的模拟结果。

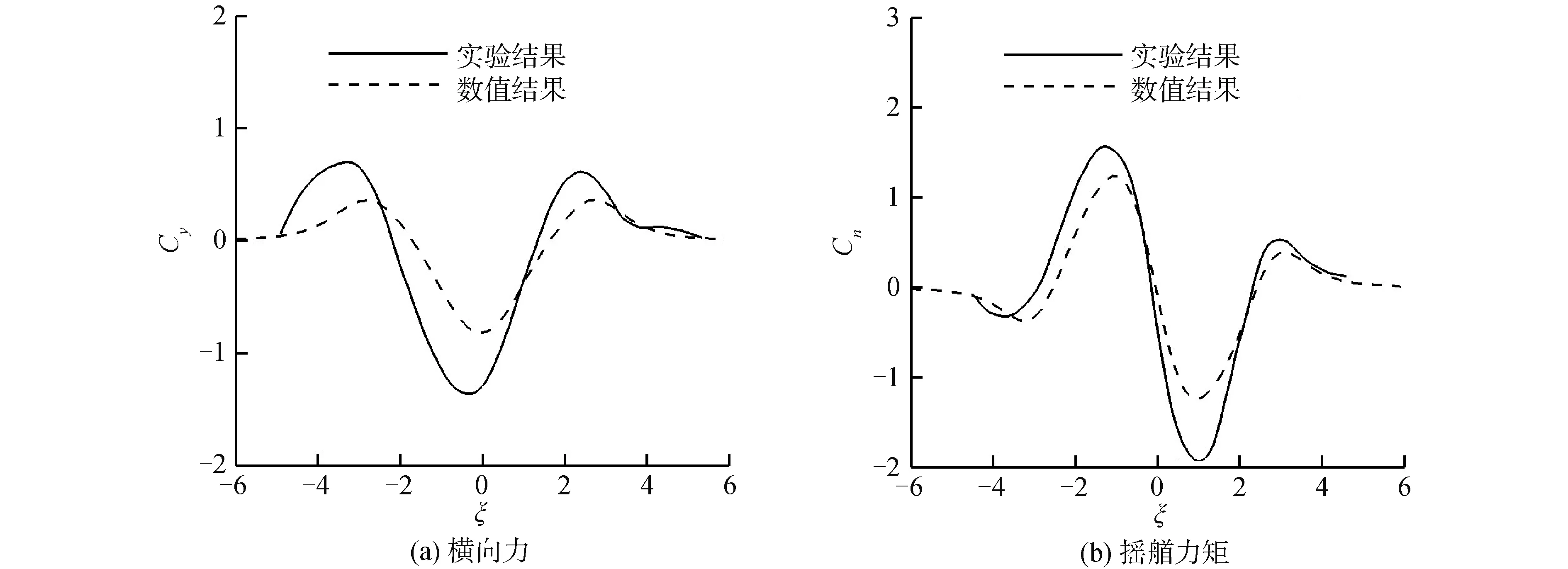
图11 工况1中油船受的水动力干扰力Fig.11 The hydrodynamic interaction forces acting on the tanker in Case 1

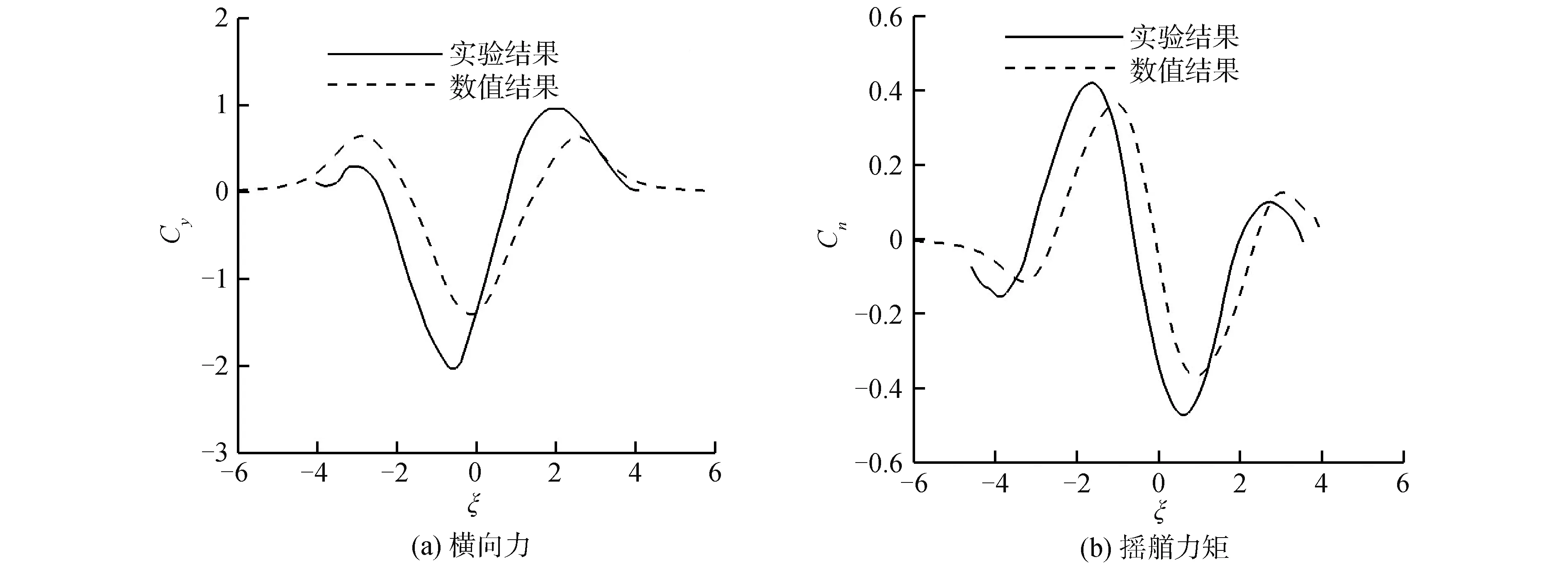
图12 工况2中油船受的水动力干扰力Fig.12 The hydrodynamic interaction forces acting on the tanker in Case 2

由图11(a)和图12(a)可见，当两船距离不断变小时，作用于油船的横向力先表现为排斥力，后表现为吸引力，并在ξ=0附近达到最大值。然后横向力随着两船的距离不断变大也逐渐降低。由图11(b)和图12(b)可见，转艏力矩的峰值大约出现在ξ=±1时。以ξ=-1为例，货船的船艏与油船的船尾位于同一纵向位置，由于两船之间的流速较高，货船的船艏与油船的船艉的压力会降低。由于此刻低压区对应的力臂最大，因此转首力矩在此时达到极值。当ξ=0时，两船相对距离最小，船体表面的低压区转移到船体舷侧。此时低压区的压力最低，低压区面积最大，因此船舶收到的横向力最大，但由于此时低压力臂最小，所以作用于船体的摇艏力矩很小。对比两工况的干扰力，可发现：工况1的水深大约是工况2的一半，但干扰力的峰值却增大了4～5倍，说明了水深对船舶水动力干扰的显著影响，也印证了研究限制水域内船舶水动力干扰的重要性。

对比试验结果可发现，不计自由液面效应与粘性效应的势流方法能够较好地预报船舶赶超过程中的干扰力趋势；但由于忽略了粘性和自由液面效应，在干扰力极值附近，数值结果数值结果均小于试验结果。对比两工况的预报极值可发现：本文使用的数值方法能够更好地预测大水深情况下的船舶水动力干扰。当水深较小时，由于忽略了上述因素且未考虑船舶升沉姿态变化，该势流方法在干扰力极值附近的计算精度较低。

2.4.2 会遇工况

图13、图14和图15分别是两船平行相遇过程中的油船受到的船舶水动力干扰，其中图13是工况3的模拟结果，图14对应工况4。图15对应工况5的结果。与2.3.1节相比，在本节模拟的会遇工况中，两船均有一定航速。

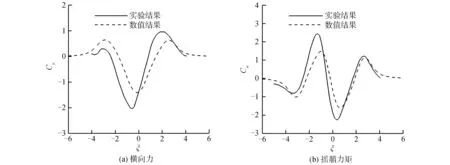
图13 工况3中油船受到的水动力干扰力Fig.13 The hydrodynamic interaction forces acting on the tanker in Case 3

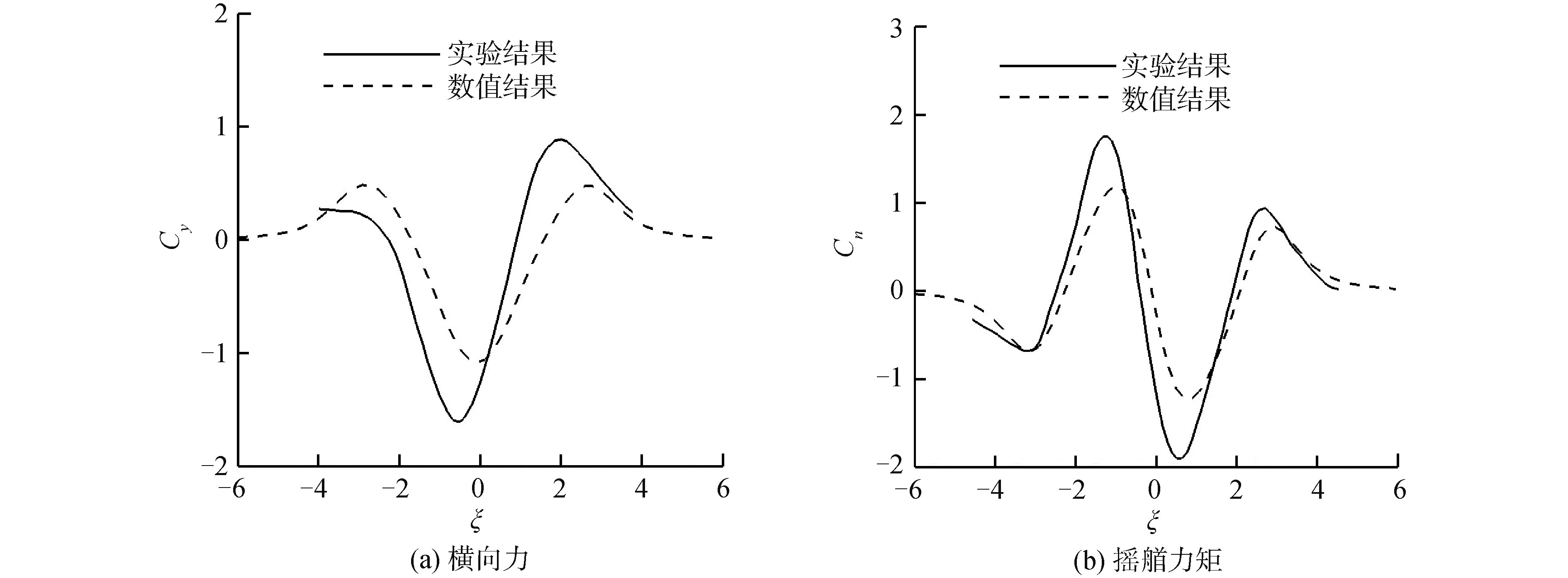
图14 工况4中油船受到的水动力干扰力Fig.14 The hydrodynamic interaction forces acting on the tanker in Case 4

图13～15分别是油船在工况3～5中受到的横向力。与上节对比发现，两船面对面会遇过程中的干扰力变化趋势与赶超过程相同。对比3个工况发现：工况4中两船横向距离最大，两船速度最小，所以工况4中的干扰力最小；工况5相较于其他2个工况，两船的水深傅汝德数都较大，所以工况5中的转艏力矩曲线的第1、4极值与2、3相近。

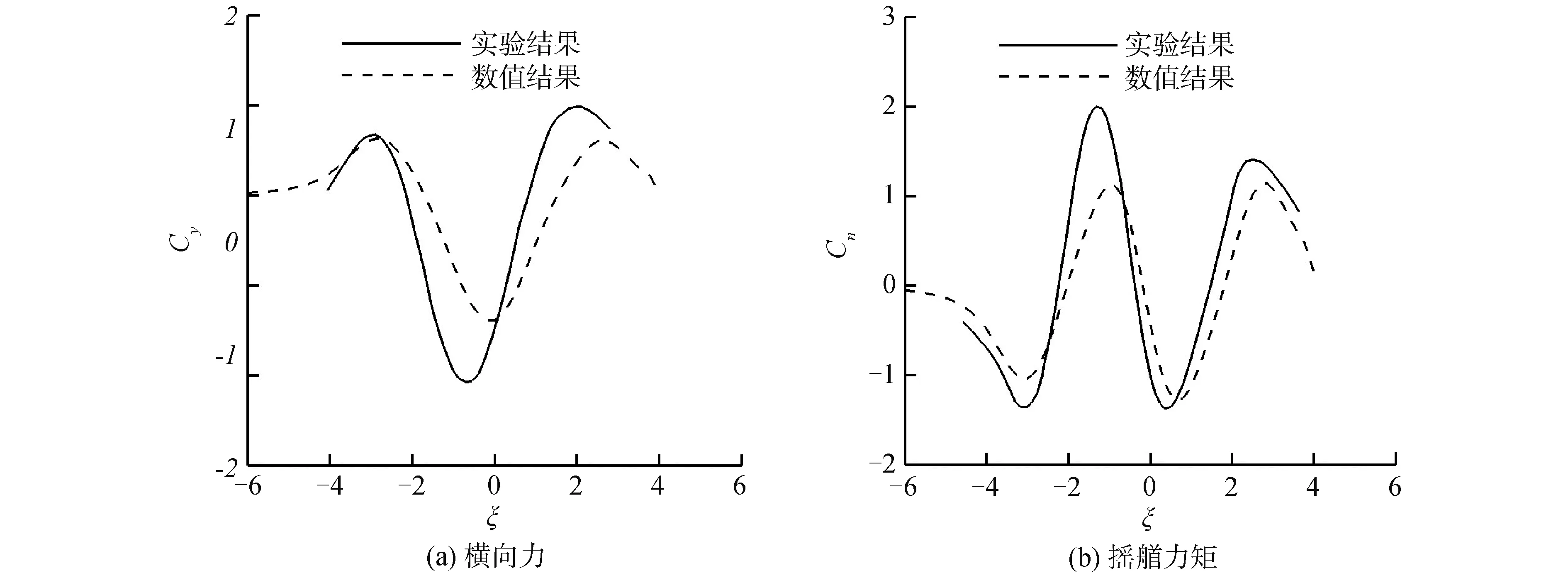
图15 工况5中油船受到的水动力干扰力Fig.15 The hydrodynamic interaction forces acting on the tanker in Case 5

与试验结果对比发现：数值方法能够有效地预测两船会遇过程中船舶水动力干扰的变化趋势，但数值结果与试验结果在干扰力极值区域仍存在一定差异，且均小于试验结果。对于数值结果与试验结果存在差异的原因，主要为没有考虑粘性效应和没有考虑自由液面变化，此外船舶姿态对船舶水动力干扰也有一定的影响。由于文献可用于方法验证的工况较少，本文并没有进行系统地对比分析，研究不同水深、横向距离与船舶航速下，以上4个因素对船舶水动力干扰的影响与作用。

3 结论

1)通过与实验结果对比，验证了不计自由液面变化与粘性效应的势流理论方法能够捕获限制水域内船舶水动力干扰的主要成分，并准确预测其变化趋势，但该方法在预报干扰力极值时，计算精度仍有不足。从工程应用的角度讲，该方法计算效率高，计算精度可接受，从一定程度上可为限制水域船舶避碰与自主航行提供支撑。

2)由于忽略了粘性效应、自由液面效应以及船舶姿态对船舶水动力干扰的影响，在某些极端工况下该方法精度有限。在中浅水 (h/T>1.5)，中低航速下本方法有着更好的精度。

3)本文仅对该方法进行了初步的验证，只计算了典型工况，实际应用中需通过系列模型试验与粘性流数值模拟等手段对本方法进行更深入和系统的验证。