基于卷积神经网络的步态周期检测方法

王科俊， 刘亮亮， 丁欣楠， 胡钢， 徐怡博

(哈尔滨工程大学 智能科学与工程学院，黑龙江 哈尔滨 150001)

步态识别作为一种生物特征识别方法，被认为是远距离身份识别中最具潜力的识别方法之一[1]。与人脸和指纹等其他生物特征相比，它不需要与受试者配合或接触。因此，步态识别在安全监控、人机交互、智能门禁等领域都有良好的应用前景。近年来，步态识别方法的研究也引起了广泛关注，并提出了许多有效的算法[2-3]。

步态周期检测是实现基于视觉的步态识别的一个重要步骤。与其他生物识别技术不同，步态识别主要依据人体在行走过程中的动作习惯完成身份识别，故不适用于利用单一的步态帧图像进行步态识别。因此，步态识别的输入是视频序列(连续图像)而不是单张的步态轮廓图像。而步态周期检测是指判定输入视频合适长度的过程，一个步态周期通常包含具有完整的步态动作特征的最少的帧数。检测得到的步态周期过短，可能会导致丢失有效的步态特征，而检测到的步态周期过长，可能会使输入包含冗余数据，占用更多的计算资源。对于比较常用的类能量图像的步态识别方法，需要步态周期检测过程作为前端的预处理步骤，而步态周期检测的结果也直接影响了类能量图步态识别结果的准确性[4-5]。

现有的关于步态周期检测的许多研究都是基于人体行走的几何特征实现，Collins等[6]提出了一种利用人体的宽度和高度进行周期检测的方法，但该方法受人与摄像机之间的距离变化的影响较大；Lee等[7]利用标准化后的轮廓宽度来检测行人步态周期，解决了距离变化的问题。Wang等[8]考虑到不同视角下轮廓大小的变化，提出了一种基于高宽比的方法，省去了标准化过程。Wang等[9]选择腿的平均宽度作为特征来进行周期检测，避免了服饰和背包的影响。此外，身体的面积也可以有效地表示周期特征，Sarkar等[10]利用腿的面积作为的特征完成周期检测。Ben等[11]提出了一种双椭圆拟合方法，将整个轮廓的2个区域拟合为被质心分割成2个椭圆，步态起伏被构造为一个周期函数进行检测。这种基于几何特征的方法简单有效，在近90°的侧视视角上达到了很高的精度。但对于不同的环境(不同的视角或服饰等)，检测精度不理想，没有很好的鲁棒性。

近年来，卷积神经网络(convolutional neural network, CNN)[12]自提出以来，就以其在基于图像的特征学习的中展现优势而受到广泛关注。Lenet-5模型是基于卷积神经网络设计的第一个网络[13]。而自2012年Krizhevsky等提出Alexnet网络用于ImageNet大规模视觉识别挑战以来，卷积神经网络更是成为了几乎所有优秀算法的核心部分，而AlexNet以其优异的成绩获得了冠军[14]。VGG是继Alexnet之后在ImageNet竞争中取得良好成绩的网络之一[15]，它继承并深化了Lenet和Alexnet的一些框架。之后，GoogLeNet[16]、ResNet[17]、 Xception[18]和DenseNet[19]等网络更是通过精巧的结构设计进一步提高了卷积神经网络在特征提取性能。而卷积神经网络出众的特征学习能力也可用于步态周期检测中。对于步态周期检测任务，CNN可以自动提取步态轮廓序列的周期特征，相对于传统方法中的单一人工特征，基于CNN的步态周期性检测方法可以达到更好的效果和鲁棒性，从而提高步态识别在复杂场景下的识别精度。本文基于CNN提出了基于分类和回归拟合的步态周期检测，采用卷积神经网络进行步态周期特征提取，完成最终的步态周期检测。与已有的方法相比，该方法减低了周期特征提取的难度和计算量，并可在跨视角条件下进行步态周期检测。

1 基于卷积神经网络的步态周期检测方法

本文提出了2种用于步态周期检测的方法：基于分类的建模思想和基于回归拟合的建模思想。基于分类建模思想的方法，简单地将步态周期检测抽象为分类任务，根据每个姿态在步态周期的位置进行分类。如图1所示，一个步态周期的过程可以分为4个部分，右双腿支撑、右单腿支撑、左双腿支撑、左单腿支撑[20]，根据不同的4个阶段将其过程分为4个类别。当分类的类别输出重新开始(即返回1)时，即得到一个完整的步态周期。而基于回归拟合的建模思想方法，考虑到分类思想中类别的边界并不十分明确，单纯的使用离散的类别数标定整个步态周期过程可能误差较大，故考虑将步态周期性变化拟合为正弦函数，更为精确地表示其周期性变化过程。如图2所示，根据正弦函数值表征步态周期特征，并定位每一帧在周期中的相应位置，当函数波形完成一个周期时，即得到一个步态周期。

图1 基于分类的步态周期建模Fig.1 Modeling human gait cycle using classification

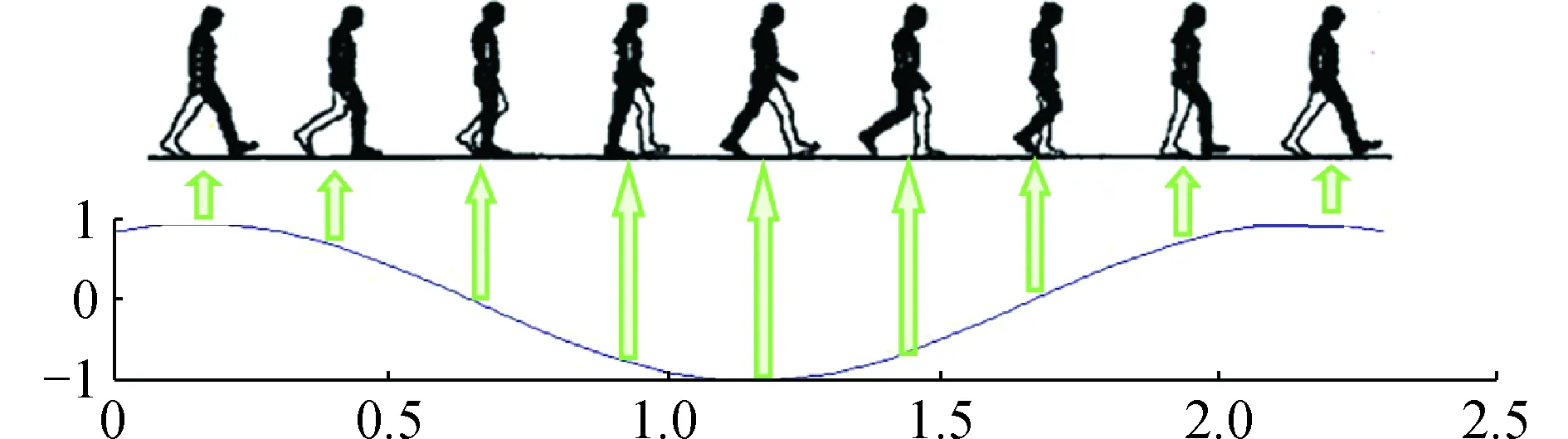
图2 基于回归拟合的步态周期建模Fig.2 Modeling human gait cycle using regression fitting method

1.1 基于分类的步态周期检测方法

根据步态周期的过程特性将步态周期检测抽象为分类问题。如图3所示，步态轮廓序列在标准化后被送至卷积网络以提取以类别为表征的周期性特征。当输出类别的完成一个循环时，则可得到一个步态周期。

标准化的目的是使所有轮廓的大小相等，以避免人与摄像机之间的距离和角度变化的对轮廓的影响。步态序列的每一帧都应该裁剪和调整至相同大小，通过定位轮廓的顶部和底部像素来提取行人的区域，然后计算其重心。利用重心、轮廓高度和宽高比(11/16)将每一帧裁剪成88×128的行人轮廓图。将标准化后的步态序列送入训练好的网络中，根据网络输出的类别判定步态周期。

在小学教学中，足球教学质量的提高离不开学校、教师、学生三方面的共同努力。学校方面应当按照新课程改革对小学体育足球教学的要求，为学生合理地安排足球课程，并采取理论与实践相结合的方式，积极地展开足球训练。同时，教师要明确足球教学对于学生身心发展的意义，深入了解学生的身体素质，并据此制定合理的教学目标，循序渐进地提高学生的足球运动能力。除此之外，教师还要向学生积极地宣导学习足球的重要性，以激发学生学习的动力，形成学校、教师、学生三者相互配合、共同进步的足球教学体系。

1.1.1 周期的分类建模

根据经典的步态周期的定义，一个步态周期的过程可以分为4个部分，右单腿支撑、右双腿支撑、左双腿支撑、左单腿支撑[20]，故本文以此为依据，将一个步态周期分为4类。如图4所示，4类步态轮廓分别对应了步态周期中行人的不同行进过程。

图3 基于分类思想的步态周期检测方法的流程Fig.3 The process of gait cycle detection based on classification

图4 4分类的步态周期建模Fig.4 Modeling human gait cycle using 4 classification

则对于输入的步态序列{F1,F2,…,FN}，通过标准化后得到{FN1,FN2,…,FNN}的标准步态序列。通过卷积神经网络S(FN)，得到相对应的输出的分类结果{C1,C2,…,CN}，其中由于将步态周期进行了4分类建模，当C1与Ci的分类结果相同，且{C2,C3,…,Ci-1}中按顺序包含其他分类结果时，即{C1,C2,…,Ci}为一个步态周期。

1.1.2 网络结构

CNN[9]是一种将步态帧依据步态周期特性进行分类的工具，它用于学习帧的周期特征并在步态周期中定位。因此，网络的输入是步态帧(128×88×1)序列，输出相应的分类结果。

因为图像分类任务在深度学习中被广泛应用并取得了良好的分类效果，故本文采用已有的经典的用于图像分类网络框架。考虑到步态帧为二值化后的步态轮廓图，本质为黑白图像，表征形式较为简单，因此采用较为简洁经典的前向网络框架：Lenet-5、AlexNet和GoogLeNet。Lenet-5包括3个卷积层(5×5)、2个池化层和1个全连接层；AlexNet包括5个卷积层(1层5×5与4层3×3)、5个池化层和3个全连接层；而GoogLeNet提出了Inception结构，如图5所示，通过增加网络的“宽度”来加深网络复杂度，使用并行的1×1,3×3,5×5卷积层和池化，同时提取不同尺度的特征，然后通过1×1的卷积对每个分支进行降维后将结果合并。

1.2 基于回归拟合的步态周期检测方法

考虑到步态帧的连续性可能导致分类边界不是十分明确，由此可能在分类结果中有较大误差。在基于分类思想的基础上，本文提出了一种将步态序列拟合成正弦函数来确定步态周期的新方法。如图6所示，步态轮廓序列在标准化后被送至卷积神经网络以提取周期性特征。然后对输出进行滤波，找出步态周期的关键帧(波峰或波谷的对应帧)，每个波峰(波谷)之间的帧即构成一个步态周期。

图6 基于回归拟合思想的步态周期检测方法的流程Fig.6 The process of gait cycle detection based on regression fitting method

标准化方法同周期的分类建模一样。完成标准化后，将步态轮廓按顺序输入到训练好的网络中，每帧的输出值通过CNN的学习表示其周期性特征，最终得到由步态序列的输出值组成的与正弦函数相似的波形(水平轴表示帧数，垂直轴表示输出值)。

最后，采用均值滤波方法对输出波形进行平滑处理。因为个别帧的函数值错误可能影响了最终的周期检测结果。但通过滤波处理后，只要帧的大部分输出是相对精确的值，就可以通过滤波来避免少量错误带来的扰动。

1.2.1 步态周期的正弦函数建模

将步态周期建模的目的是将每个帧的步态周期特征量化为数值。用正弦函数作为低维信号来表示步态序列的周期性波动。正弦函数作为一个简单的连续的周期的函数，且在一个周期内存在一个波峰(极大值)和一个波谷(极小值)的性质，与一个步态周期中左右腿分别行进一步的周期性规律十分契合，故采用正弦函数作为一个标准步态周期的建模。且可以将2次最大步伐(左腿在前与右腿在前)帧对应正弦函数的波峰与波谷，而波峰和波谷更容易作为关键帧进行定位，从而获得一个步态周期。

具体地，选取周期为1，幅度为1的正弦信号作为低维信号用于表征步态序列的周期性。为了保持评价周期特征的一致性，本文定义了一个用于对应于步态输出值和周期特征的标准。在一个步态轮廓序列中，两腿并拢且右脚有向前迈的趋势的视频帧为起始位置，经过一个周期的序列之后，两腿再次并拢且右脚有向前迈趋势的帧为该周期的结束位置。此时这一帧图像可以作为上一个周期的结束，又可以作为这一周期图像的开始，起始和终止位置帧的函数值为0。当定位好起始位置和最终位置之后，中间位置的标记值根据平均值的正弦函数来计算，则有训练集中每一帧的函数值为：

式中：Li步态视频中的第i帧的函数值;N表示该帧所在的步态周期共包括N帧;n表示该帧为所在的步态周期中第n帧。如图7所示为一个包含24帧的步态周期，故间隔为1/23，周期的每帧的位置分别为0、1/23、2/23、3/23、…、1。然后，sin(0)、sin(1/23)、sin(2/23)、sin(3/23)、…、sin(1)。通过这种方法，步态周期特性被作为正弦函数来表征。

1.2.2 网络结构

本文采用CNN学习步态帧的周期特征和在步态周期中定位，将步态帧拟合成正弦函数。因此，网络的输入是步态帧(128×88×1)序列轮廓，输出是相应的函数值。在用于分类思想的网络框架上，本文设计了3种不同深度和宽度的步态周期性检测网络结构，并采用均方误差(MSE)作为它们的损失函数。

图7 24帧的步态周期的正弦拟合Fig.7 Gait cycle detection of 24 frames based on sine fitting algorithm

表1详细显示了用于步态周期性检测的基本网络的结构。Conv7表示7×7核的卷积层。同样，Conv5有5×5个内核，Conv3有3×3个内核。利用较大的卷积核初步提取周期特征。最后一层的神经元数量是1，因为输出应该是一个回归值。所有的激活函数都是Relu。在基础网络的基础上，对网络结构进行加深，具体的结构如表1中加深网络所示，其中相应地，Conv3同样为3×3核的卷积层。而输出层相同，是一个具有Relu激活功能的神经元。与基础网络的区别在于采用较小的卷积核，卷积序列可以模拟更大的感受野并减少计算量。另外，利用Inception[21]对网络的宽度进行扩展，如表1中的加宽网络所示，不仅使网络的深度增加，还可以改进网络的宽度以改善网络性能。

2 实验结果与分析

本文在中科院CASIA-B步态数据集[22]上进行了不同网络结构下和不同视角下的步态周期检测的实验。并与现有的周期检测方法进行对比。在CASIA-B步态数据集中，共有124个行人，其中每个行人有11个视角(0°, 18°,…, 180°)，每个视角下有10个步态序列。

卷积神经网络需要从大量标注的数据中学习。因此，有必要将每个帧的周期特征标记为训练的标签。每个帧的函数值表示其周期性特征作为训练集中的标签。手动定位了周期序列的初始位置，并通过计算得到了标签(类别和对应的函数值)。其中共有96 000多个图像被手动标记以供训练。

表1 网络结构Table 1 The structure of network

用于回归拟合方法的步态周期检测网络是使用具有MSE损失的Adam进行训练的。Adam参数设置为默认值，即β1为0.9，β2为0.999。同时，使用均值为0，方差为0.01的正态分布初始化权重。Batch_size设置为128，学习率为0.001，经过75 000次迭代后停止训练。

2.1 评价指标

本文定义了一个直接的度量来评估步态周期性检测的性能的评价指标，通过表示误差与实际周期的比率来度量步态周期检测精度：

式中：T是实际周期中的帧数；Ts是检测到的数目。C值越小，误差越小，方法得到的精度越高。相反，C值越大，性能越差。

2.2 基于分类的步态周期检检测结果

根据分类的建模思想，将步态帧进行分类，分类结果的正确率如表2所示。其中Alexnet的结果要略高于Lenet，这可能是由于Lenet网络过于简单，Alexnet在此基础上加深了网络，取得了更好的分类结果。而GoogLenet的效果与Alexnet相近，但略有下降，这可能是由于步态轮廓图相对较为简单，过于复杂的网络可能会导致过拟合。但所有网络模型的分类正确率都较低，这可能是由于步态序列中，相邻帧的差异较小，分类的界限并不十分明确。

表 2 不同网络模型下的分类正确率Table 2 The classification accuracy of different networks

将一个待测步态轮廓序列按照顺序输入训练完成的卷积网络中，完成一个分类循环时，即得到一个周期的步态轮廓图像。具体的周期检测如表3所示，通过C来评价步态周期检测精度。其中Alexnet网络的平均误差最小，取得了最好的识别结果，这也与表2中的分类结果一致。而在36°、108°和126°时，C小于0.1，平均误差只有1～2帧，是令人满意的检测结果。值得注意的是，通常情况下普遍认侧面90°包含最多的步态信息，但在90°时，周期检测结果的误差相对较大，这可能是由于步态轮廓图在此时是十分对称的，难以分辨运动的是左腿还是右腿，定位其在步态周期中的位置不够准确，导致了误差相对较大。

表3 基于分类的步态周期检测方法性能Table 3 The performance of gait cycle detection using classification

2.3 基于回归拟合的步态周期检测结果

根据正弦函数的拟合方式，将步态轮廓按顺序输入到训练完成的网络中，利用网络提取周期特征。对于每个帧，可以得到一个表示其周期性特征的输出值。因此对于一个轮廓序列，可以得到一个一维向量。通过定位波形的相邻峰值，则可以确定步态周期(相邻波峰或波谷之间的帧为一个步态周期)。图8显示了由3个网络以不同视角下的周期检测的滤波波形，可以看出波形具有良好的周期性，类似于正弦函数，其中基本网络的性能最好。所有3个网络在斜视图(如18°、36°和144°)附近工作得更好。这可能是由于拟合的方式导致的，因为函数值主要受步幅宽度和左右脚顺序的影响。宽度步长越大，输出的绝对值越大，如表1所示，而左脚或右脚的顺序决定函数值的符号，当右脚向前时，这个符号是正的。0°和180°的视角中，步态轮廓包含的步长特征较少，而90°的步态轮廓包含的区分左脚和右脚的特征较少，故该方法在0°、90°和180°这3种角度下效果较不理想。

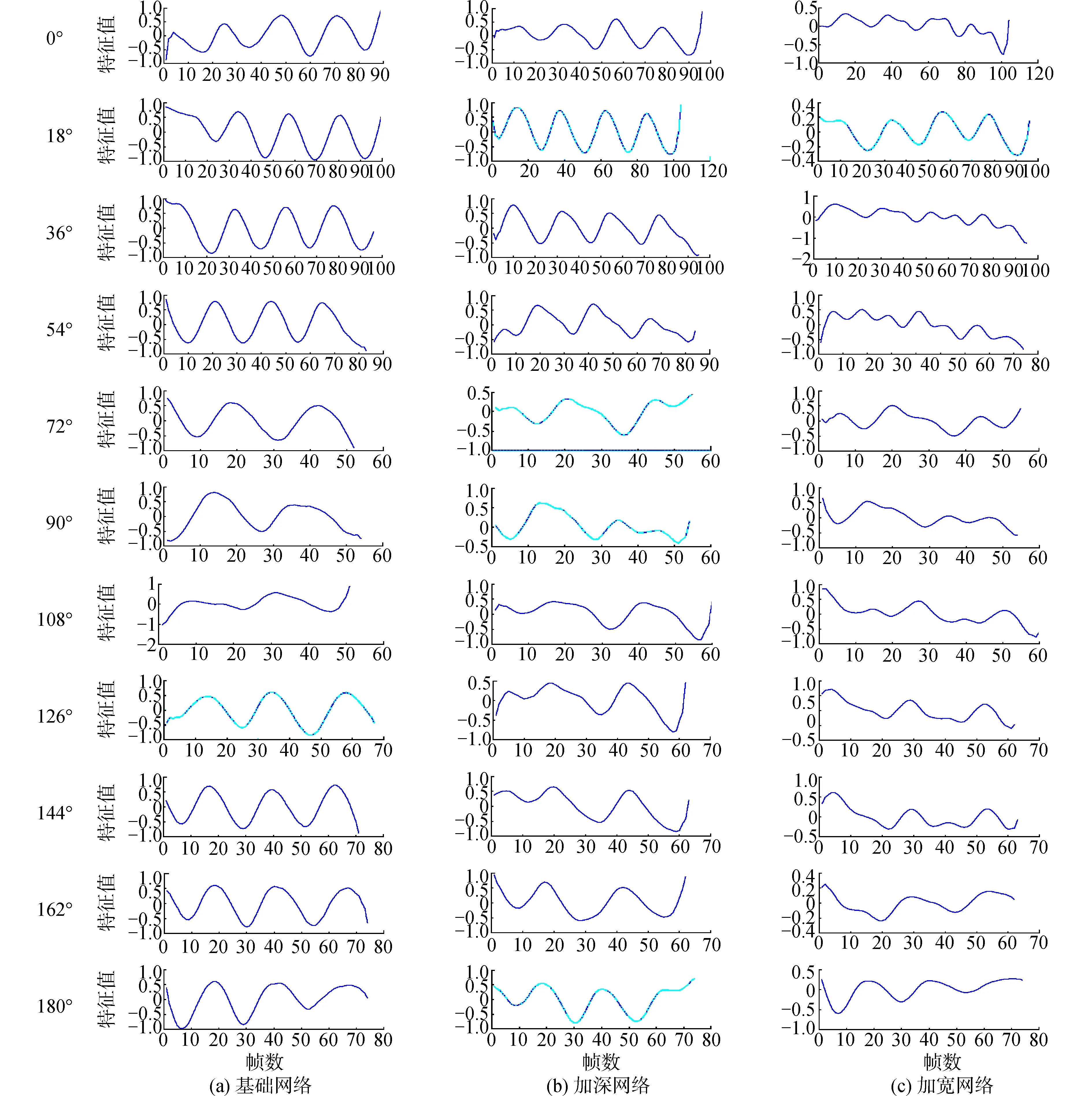
图8 不同角度下不同网络结构下的输出波形Fig.8 The waveforms of different network structures under different views

表4展示了采用的每个网络的周期检测的量化性能。3个网络的检测周期都是较为准确的。其中在几个网络中的不同角度下，都有C接近于0的情况，说明步态周期检测性能良好，误差较小。而基本网络是本文提出的模型中最好的一个，能够较为有效地检测各视角下的步态周期。由于步态轮廓是二值图像，以边缘特征为主，因此基本网络的深度足以提取其周期特征并输出精确值。其C的平均值低至0.06，按25帧的实际平均周期计算，平均误差约为1.5帧。另外2个网络的C也不高，分别为0.13和0.14。实验结果表明，该方法对步态周期的检测是有效的，并且对不同的视角具有鲁棒性。

表4 基于回归拟合的步态周期检测方法性能Table 4 The performance of gait cycle detection using regression fitting method

2.4 与其他方法的对比

图9展示了不同方法的步态周期检测的性能，其中选择了几种能够在所有视角下(0°～180°)工作的方法，以便进行比较。其中基于宽高比[8]、腿部平均宽度[9]、腿部面积[10]、双椭圆拟合[11]的步态检测方法是较为传统的方法是通常为较为传统的方法，这意味着其步态周期检测误差在0°和180°附近是比较大的。相比之下，本文提出的基于卷积神经网络的方法，无论是基于分类思想还是回归拟合思想，在正面视角和背面视角上都取得了较好的效果。而基于回归拟合的周期检测效果优于基于分类的方法，这是由于步态序列是一个连续的渐变过程，分类的界限相对不明晰，因此将其作为周期函数建模更为合理。

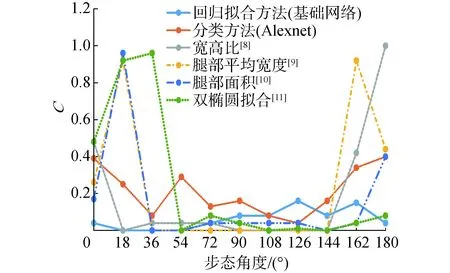
图9 实验结果对比Fig.9 The comparison of the experimental results

在接近90°的视角时，所提方法的误差略大于传统方法，但在所有视角中，基于回归拟合方法的C最大为0.16。也就是说，误差大约是3～4帧，相对于包含约25帧的步态周期，这样的误差是可以被接受的。故利用卷积神经网络在不同视角下进行步态周期性检测是可行的，弥补了以往方法在前视图和后视图上精度较低的缺点。因此，该方法能够有效的检测步态周期，且对视角变化有很好的鲁棒性。

3 结论

1)实验结果验证了提出的基于分类和回归拟合的卷积神经网络步态周期检测方法对于不同视角的步态识别的有效性和鲁棒性，弥补了以往方法在前视图和后视图上精度较低的缺点。

2)在所有视角下的步态序列中，基于分类和回归拟合的卷积神经网络步态周期检测方法均在斜视角下(如18°和144°)的识别率较高，在0°、90°和180° 3种角度下效果相对不够理想。

3)本文主要计算步态周期的步态能量图作为特征，步态序列相邻帧的运动信息可能会忽略，因此下一步将研究融合几何特征、时序特征的长短期记忆网络(LSTM)的步态周期检测方法，进一步提高其准确率。