脐带缆拉弯组合疲劳试验机恒拉力控制

王贤成， 李伟， 刘毅,， 闻中翔

(1.浙江大学 流体动力传动与控制国家重点实验室，浙江 杭州 310027； 2.宁波大学 科学技术学院，浙江 宁波 315100; 3.浙江大学 宁波理工学院，浙江 宁波 315100)

随着深海油气勘探的发展，脐带缆作为在水下生产系统与浮动平台之间起连接作用的一种重要的设备，被广泛地应用于深海油气输送项目中。目前最新研制成产的脐带缆可以在水深超过2 700 m的海域正常工作，其单根铺设长度已超过140 km[1]。在复杂的海洋环境中，由于受到海浪、波流的冲击，脐带缆与浮体连接处会受到横向低频小角度的弯曲力。在浮体升沉以及其自身重力的影响下，脐带缆的加剧摇摆导致施加在脐带缆上的轴向拉伸力较大。因此一般可以将脐带缆在实际工况下的受载特点简化为承受轴向拉伸力与弯曲循环应力组合载荷。

此外，脐带缆的非线性弯曲特性使其在使用过程中极易产生疲劳损伤[2-5]。因此，为保证其在整个寿命周期内能够正常工作，通过拉弯组合疲劳试验系统模拟脐带缆在海洋工况下的受载特点，对脐带缆的疲劳寿命进行研究的工作至关重要。根据脐带缆疲劳试验要求[6-7]，轴向拉伸力应保持为一个较大的恒拉力。所以为了提高脐带缆疲劳试验的可信度，需要对脐带缆的拉伸端进行恒拉力控制。

由于电液力伺服控制系统具有较大的推重比、较快的响应速度以及较高的输出力控制精度，使得其在工业中得到了广泛应用。但由于电液力伺服控制系统中存在的非线性因素以及其自身的时变性因素[8-9]，导致系统输出拉力难以得到精确控制[9]，另外，作为系统的负载，脐带缆自身的非线性弯曲与拉伸特性也会对系统输出的精度产生较大的影响。

传统的线性PID控制器由于其结构简单、易于实现等特点，被广泛地应用到电液力伺服控制系统中。但是当被控系统具有较明显的时变性或外界环境的影响下系统参数发生较大的变化时，PID控制系统的鲁棒性与控制精度难以得到保证。

为了解决这一问题，文献[10]在1971年将智能算法应用到电液力伺服控制系统中。在此之后，各国专家和学者对智能控制的研究越来越受到重视。Wang等[11]针对阀控单杆液压伺服系统的运动跟踪控制提出了一种基于扩展状态观测器(ESO)的非线性自适应控制方案。Li等[12]提出了一种新的模糊控制方案来控制水力。此外，在模糊控制算法和神经网络的帮助下，PID控制器对典型PID控制器的液力控制也具有较好的自适应性能和鲁棒性。将模糊控制算法与神经网络相结合，对常规PID参数进行更新。Yao等[13-15]为提高电液伺服系统的跟踪性能，开发了一种基于自适应神经网络的自适应逆控制器。

模型参考自适应控制也可以用来减小时变参数的影响。基于神经网络和李亚普诺夫理论，Yang等[16]提出了一种新的模型参考自适应控制器，用来控制电液活塞的速度和位置。顾伟伟等[17]在考虑模型不确定性和状态约束的情况下，提出了一种将模型预测控制器和鲁棒自适应控制器相结合的电液伺服系统模型参考鲁棒自适应控制方法，解决了电液伺服系统因不确定扰动和时变因素引起的不稳定性问题，但其控制精度仍不理想。

深海脐带缆由复合材料组成、且具有显著非线性弯曲。针对脐带缆刚度特性，学者相继提出一系列的用以脐带缆刚度简化计算的数学模型[18-19]，但简化精度有限。另外，由于脐带缆过长，当拉伸力发生显著变化时，脐带缆会发生振动。考虑到上述干扰因素，脐带缆疲劳试验机很难具有良好的恒拉力控制性能。为改善这一问题，本文提出一种基于自适应线性神经网络和最小均值M估计相结合的模型参考自适应控制方案。与其他模型参考自适应控制方法不同，对于自适应律，最小均值M估计算法使用更具有鲁棒性的“M估计”调整系统中的不确定参数，以提高控制精度，获得良好的动态性能。因此削弱了脉冲噪声的干扰，提高了控制系统的鲁棒性。

1 疲劳试验系统和模型描述

1.1 拉伸弯曲疲劳试验系统

拉伸弯曲疲劳试验系统主要由钢结构框架、拉伸机构、弯曲机构、液压动力及控制系统、数据采集系统、冷却循环系统组成。如图1所示，被测脐带缆长21 m，密度和直径分别为50 kg/m和0.126 m。脐带缆的弯曲端通过连接器连接到弯曲机构，由2个水平对称放置的液压执行机构为实现脐带缆的弯曲提供动力。弯曲机构在垂直方向的最大摆角范围为 -20°～20°。脐带缆的另一端通过拉伸机构连接到液压缸的活塞杆上，最大拉力为700 kN。数据采集系统由SIMATIC S7-1200、ET-200S和相应的数据转换器(A/D、D/A)模块组成。冷却塔和板式散热器用于降低液压油的温度，使系统在安全状态下工作。

图1 脐带缆拉伸弯曲组合疲劳试验机及弯曲拉伸机构Fig.1 The tension and bending combination fatigue test system for the umbilical

1.2 液压系统的控制原理及动态模型

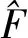
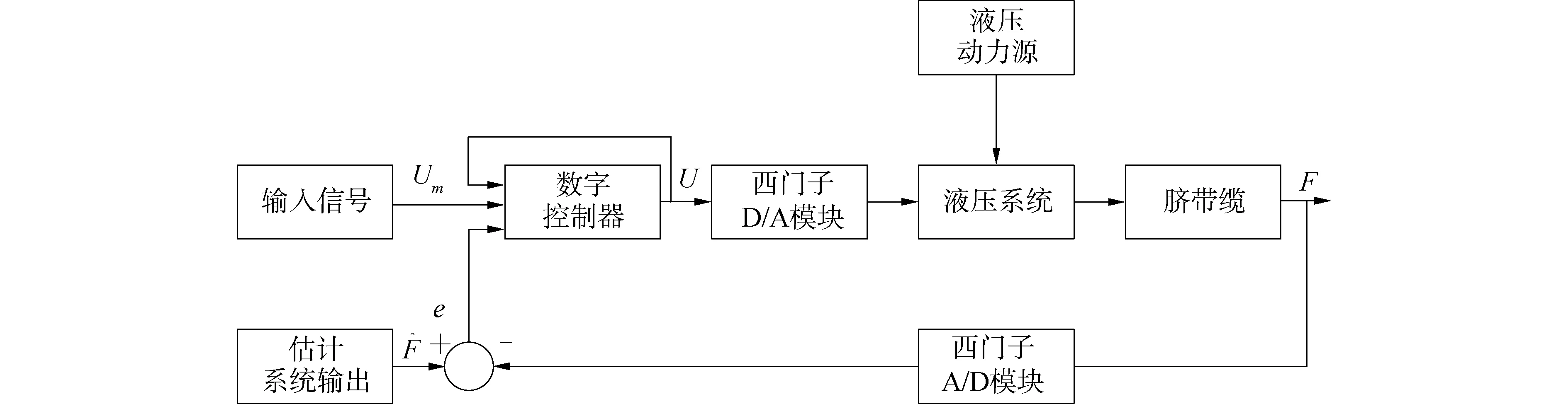
图2 阀控液压系统控制原理Fig.2 The control principal of the tension hydraulic system

图3中所示为三位四通滑阀与非对称缸构成的阀控液压缸系统原理图。P0是回油压力，Ps是油源压力，q1和q2分别是油缸的输出、输入油流量，V1和V2分别是有杆腔、无杆腔的容积，A1和A2分别是无杆腔和有杆腔的有效作用面积。m1是活塞及负载的等效质量，Bp是活塞、负载以及其他运动件的黏性阻尼系数，k是负载运动时的弹簧刚度，Xv是伺服滑阀的位移。液压缸由比例阀(MOOG D662)控制。2个压力传感器分别固定在出口和进口，用于测量实际液压油压力，从而计算脐带缆上的实际拉力。由于脐带缆具有非线性拉伸特性，其实际系统过于复杂，先将其简化为质量块、弹簧和黏性阻尼组合，而无需考虑动态弯曲的过程。工作油压Ps为16 MPa，假设液压系统中没有泄漏，液压油为无黏性、不可压缩的理想流体，油压Ps恒定不变，回油压力为0，那么上述液压系统的物理特性为：

qL=Kqxv-KcpL

(1)

(2)

式中：qL是负载流量；Kq是流量增益系数；Kc是流量-压力系数；PL是负载压力；η是折算系数。油缸内液压油流量为：

(3)

(4)

式中：mt为活塞及负载的等效质量；Bp为活塞、负载以及其他运动件的黏性阻尼系数；f和F分别为外界其他负载力和载荷力。

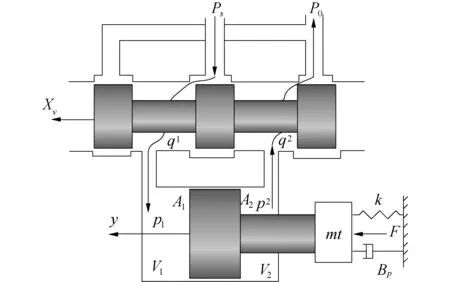
图3 阀控非对称液压缸原理Fig.3 Schematic diagram of the tension hydraulic system

在方程(1)～(4)上进行拉普拉斯变换时，不考虑干扰力，则负载力FL对阀芯位移Xv的传递函数可以表示为：

(5)

上述液压系统的主要参数见表1。

表1拉力液压控制系统的参数

Table1Theparametersofthetensionhydrauliccontrolsystem

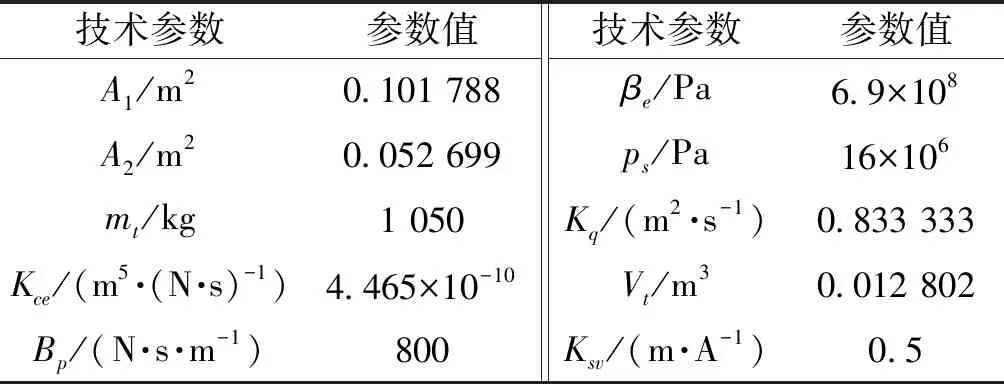
技术参数参数值技术参数参数值A1/m20.101 788βe/Pa6.9×108A2/m20.052 699ps/Pa16×106mt/kg1 050Kq/(m2·s-1)0.833 333Kce/(m5·(N·s)-1)4.465×10-10Vt/m30.012 802Bp/(N·s·m-1)800Ksv/(m·A-1)0.5

2 离散模型参考自适应控制方法设计

2.1 控制方案设计

通过零阶保持法，将系统传递函数离散化为B(z)/A(z)。将B(z)和A(z)的阶数分别设为n和m，然后用式(6)～(8)来表示液压控制系统的线性模型。根据Diophantine方程，液压控制系统的非最小实现可由式(9)中表示。

(6)

A(z)=zn+an-1zn-1+…+a1z+a0

(7)

B(z)=bmzm+bm-1zm-1+…+b1z+b0

(8)

式中u(k)和F(k)是液压控制系统的输入和输出信号。

(9)

式中:多项式Q(z)、D(z)、R(z)和H(z)的阶数分别为n、n-m、n-2、n-1;bm是需要估计的参数;R(z)和H(z)可表示为：

R(z)=rn-1zn-1+rn-2zn-2+…+r1z+r0

(10)

H(z)=hn-1zn-1+hn-2zn-2+…+h1z+h0

(11)

式中:rn-1,rn-2,…,r1,r0,hn-1,hn-2,…,h1,h0是R(z)和H(z)的系数。另外，系统输出也可以表示为：

F(k)=ΘT(k)ζ(k)

(12)

ΘT(k)=[bmrn-1…r1r0hn-1…h1h0]=

[θ1θ2…θ2n+1]

(13)

(14)

(15)

为了满足液压控制系统性能的要求，可选择Bm(z)/Am(z)=(0.442 9z+0.236 8)/(z2-0.482 3z+0.162)为参考模型。考虑到参考模型和液压控制系统，离散模型匹配控制系统如图4所示。

图5为所设计的离散模型参考自适应控制系统。系统输出F(k)应始终等于参考模型输出。

(16)

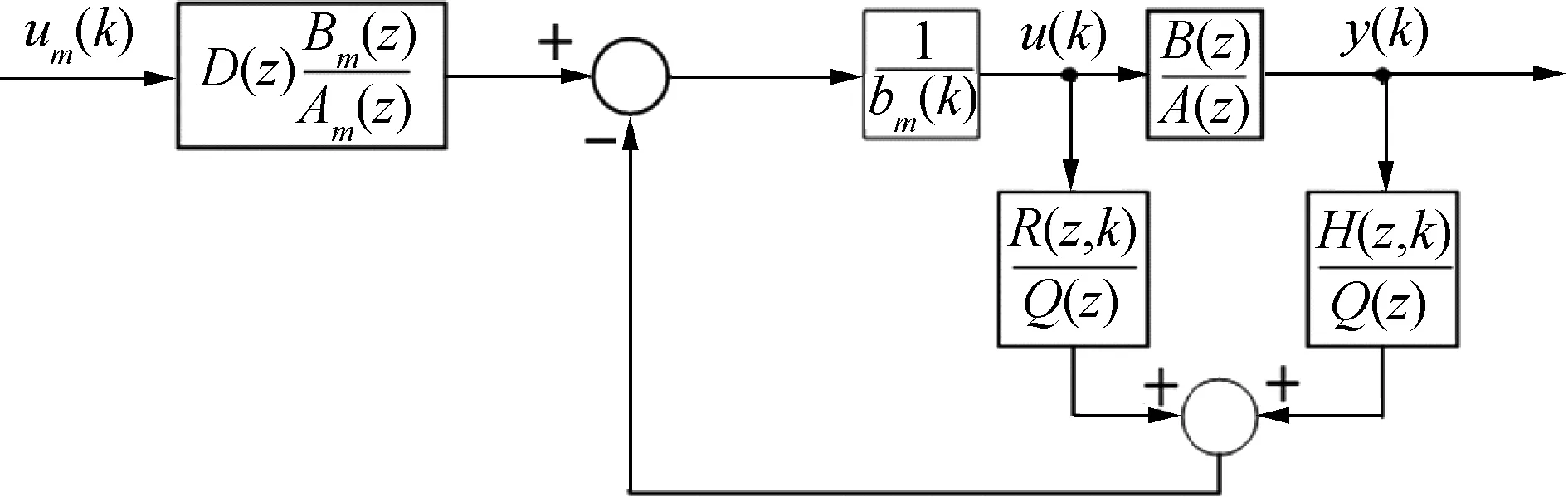
图4 离散模型匹配控制系统Fig.4 Discrete model matching control system

系统输出误差e1(k)和系统估计输出误差e(k)为：

e1(k)=Fm(k)-F(k)

(17)

(18)

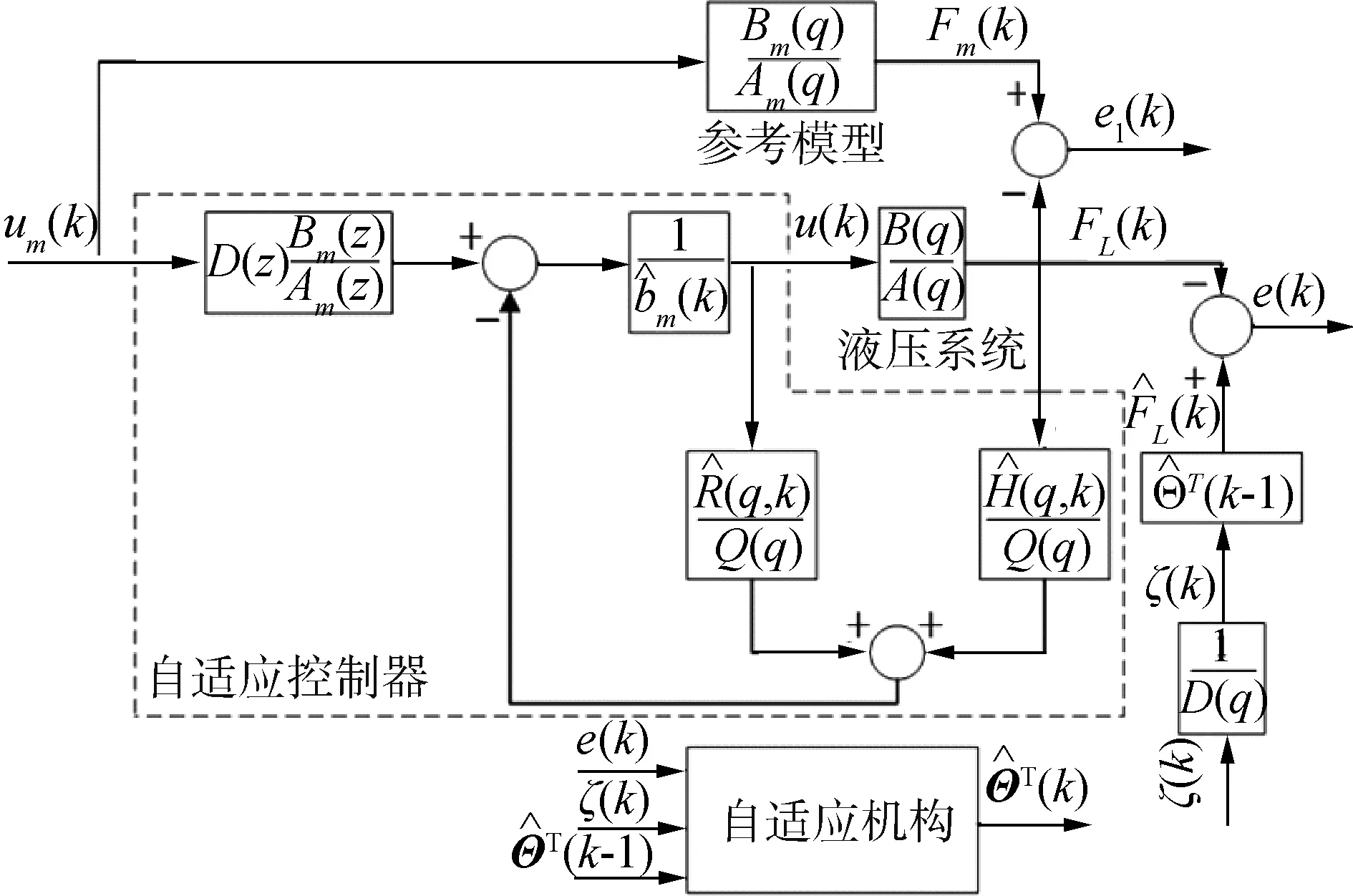
图5 离散MRAC控制系统Fig.5 Model reference adaptive control system

2.2 基于ADALINE-LMM算法的参数自适应律

为了获得更好地自适应控制性能，采用自适应线性神经网络结合最小均值M估计算法对液压控制系统进行实时参数辨识。Adaline是一种线性神经网络，输入信号利用系统估计的输出误差e(k)来调整Adaline的权值[20-23]。令目标函数为，则其表示为：

JM(k)=E{M[e(k)]}

(19)

式中M[e(k)]是一个鲁棒M估计函数，通过hampel三段式获得，表示为：

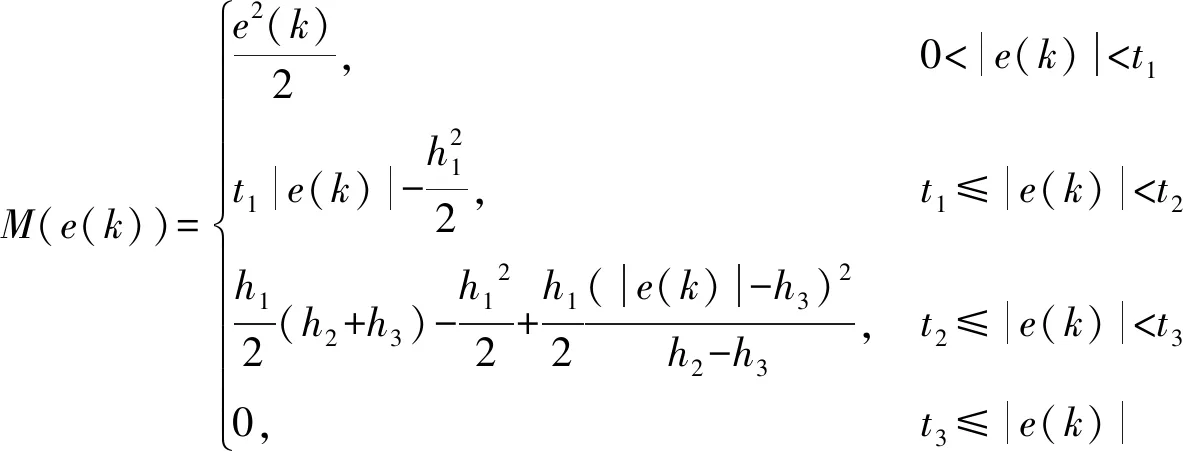
(20)

(21)

(22)

式中：t1、t2和t3是3个阈值，可用于确定脉冲抑制水平。上述3个参数可根据式(23)、(24)估算为：

C2med{e(k)2,e(k-1)2,…,e(k-Lw+1)2}

(23)

(24)

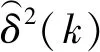
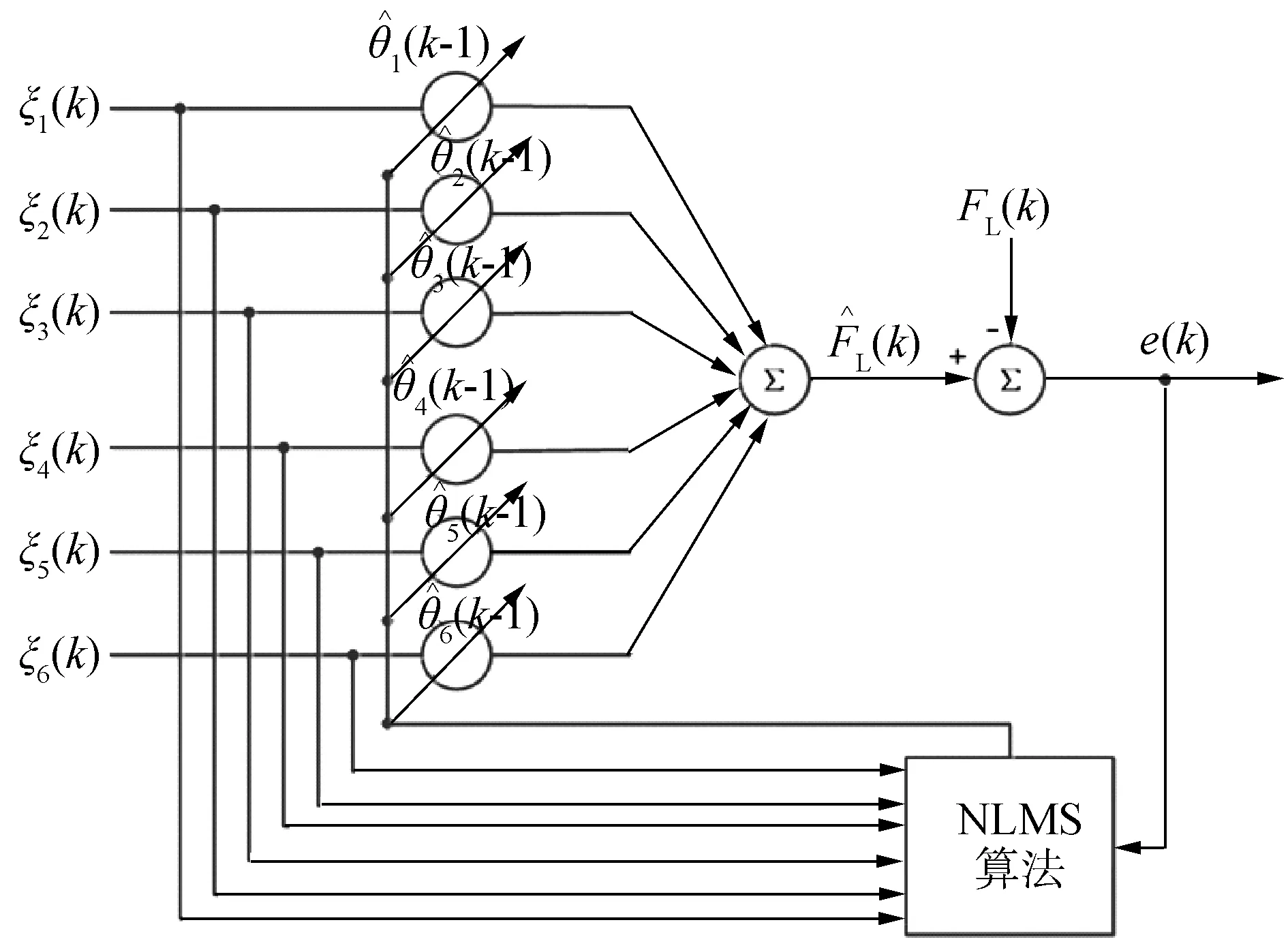
图6 系统的自适应规律Fig.6 The adaptive law of the proposed MRACS

(25)

(26)

式中μ表示提高控制方案跟踪能力的步长。

2.3 ADALINE-LMM算法的稳定性分析

为了保证ADALINE-LMM算法的稳定性，步长μ应在一个特定的范围内选择，该范围为[24-28]：

(27)

式中：R是输入自相关矩阵；λmax(R)是输入自相关矩阵R的最大的特征值。步长的上限通过给出的μmax=2/3tr(R)用于ADALINE-LMM算法中。其中，tr(R)是矩阵R的迹。从式中可看出算法的稳定性受步长μ的影响。

3 MRACS与PID输出和力控制仿真

为说明所提出的控制方案的有效性，本文利用MATLAB/SIMULINK对图3所示的阀控液压系统进行了仿真。控制系统的简化传递函数为：

(28)

其离散传递函数为：

(29)

实际上，脐带缆的非线性特性是显著的，其对整个系统的影响是不容忽视的。此外，电液力伺服控制系统本身就是一个慢时变系统。考虑这些时变元件及其相互的影响，假设离散传递函数的所有系数在试验期间在其模型值的70%～130%内变化，则系统的传递函数可写为：

(30)

(31)

如方程(31)所示，假定上述系数以正弦形式变化且f为变化频率。对于Adaline-LMM算法，C1、C2和α的最优化值分别设置为0.995 0、2.718 8和1。Lw设置为7，采样频率为30 Hz，系统输入是频率为0.025 Hz的正弦信号和振幅为100 000的阶跃信号(10～100 s)的组合。α和λ分别取1和0.548。权重的初始值都设置为0。

图7中(a)、(b)显示了当液压系统内部参数以不同频率变化时系统的控制结果。结果表明，系统输出能很好地跟踪参考模型的输出结果。虽然存在一些微小的波动，但仍处于允许范围内。

为说明所提出的MRACS相比于传统PID控制方法的优越性，在仿真过程中采用一种典型的PID控制器来作对比。PID控制器在0.1 Hz (1 Hz)的kp、ki和kd参数分别设置为10-7(1.2×10-7)，8×10-8(9×10-8)和10-9(10-10)。从图8(a)和(b)可以看出，采用PID控制器的系统输出不稳定且不能控制在目标值附近范围内，说明PID不能及时地跟踪变化，当系统参数变化较快时，采用PID控制器的液压恒拉力控制系统变得不稳定、系统输出出现明显振荡。显然，与PID控制器不同的是，当液压系统的参数发生变化时，MRACS能够提供具有较好鲁棒的恒力控制性能。

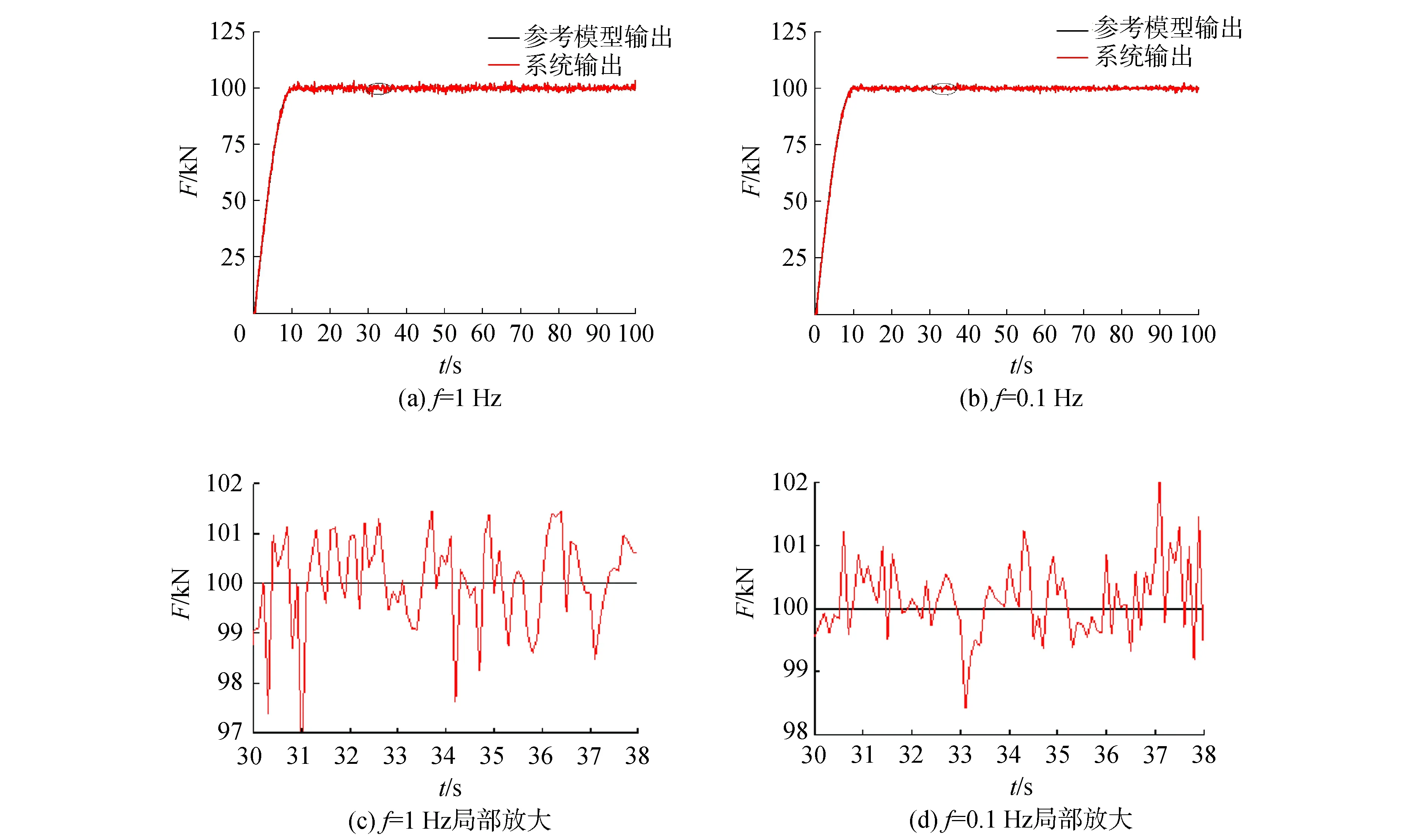
图7 MRACS的仿真结果Fig.7 MRACS simulation result

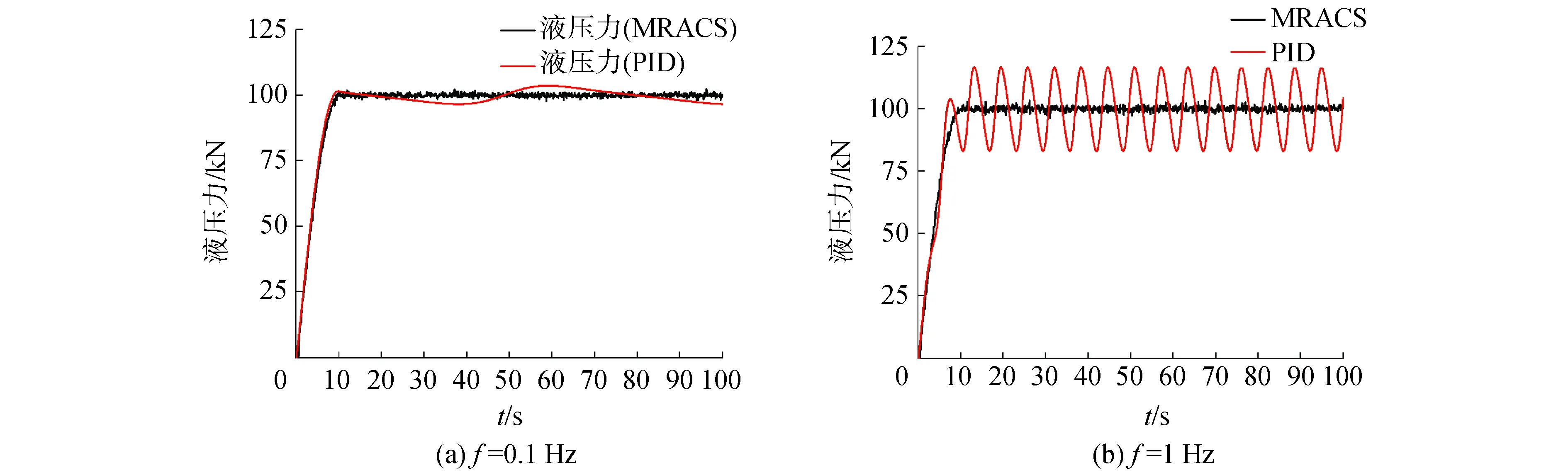
图8 恒力控制仿真结果Fig.8 Constant force control simulation result

4 实验结果

实验中控制系统参数设置与仿真条件相同。在脐带缆弯曲端弯曲成4个不同角度时，分别对系统的静态拉伸性能进行测试。然后在4种典型弯曲速度下，对系统的动态拉伸性能进行测试。

图9为系统静态拉力实验的测试结果，从图9中可看出，即使脐带缆在不同角度弯曲下其EI和EA值发生了变化，但所设计的控制系统总能将静态液压拉伸力保持在设定值周围，波动幅度较小。从表2中可得出，此时系统的静态跟踪误差最大不超过3%，平均跟踪误差接近0.3%，所以该控制器的控制性能完全能满足系统静态实验的要求。

图9 不同弯曲角度下的静态拉伸力实验结果Fig.9 Static stretching force experiment results at different bending angles

表2静拉伸试验结果的相关分析数据

Table2Therelativeanalysisdataofthestaticstretchingforceexperimentresults

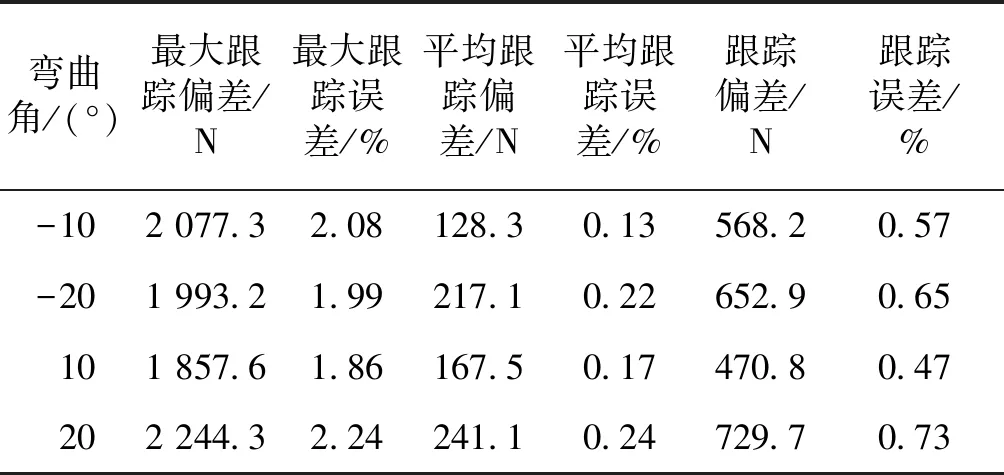
弯曲角/(°)最大跟踪偏差/N最大跟踪误差/%平均跟踪偏差/N平均跟踪误差/%跟踪偏差/N跟踪误差/%-102 077.32.08128.30.13568.20.57-201 993.21.99217.10.22652.90.65101 857.61.86167.50.17470.80.47202 244.32.24241.10.24729.70.73

根据国际标准的要求，脐带缆拉弯组合疲劳试验机还需要对脐带缆进行动态拉伸试验。脐带缆的动态试验要求脐带缆拉伸端的拉伸力保持恒定，即当脐带缆弯曲端在2个水平对置的液压缸的推动下在一定的角度范围内往复摆动时，需要电液力伺服系统仍然能够在误差为10%的范围内对脐带缆拉伸端施加恒定的拉力。

在本实验中，根据实际试验需求，选取的脐带缆弯曲角度的变化范围为 -20°～ 20°，摆动周期分别设定为140 s、80 s、60 s和40 s。相应的动态拉伸实验的结果如图10所示。此外，统计系统的最大跟踪偏差(MTD)、最大跟踪误差(MTE)、平均跟踪偏差(ATD)、平均跟踪误差(STE)以及跟踪误差(SDTE)的标准偏差，具体结果详见表3。

表3动态拉伸力试验结果的相关分析数据

Table3Therelativeanalysisdataofthedynamicstretchingforceexperimentresults

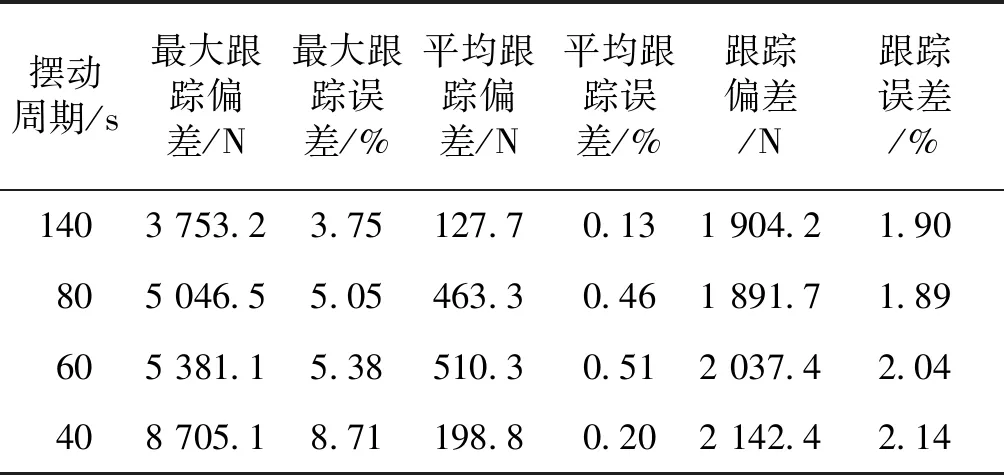
摆动周期/s最大跟踪偏差/N最大跟踪误差/%平均跟踪偏差/N平均跟踪误差/%跟踪偏差/N跟踪误差/%1403 753.23.75127.70.131 904.21.90805 046.55.05463.30.461 891.71.89605 381.15.38510.30.512 037.42.04408 705.18.71198.80.202 142.42.14

从图10可以看出，系统拉伸力的波动性似乎随着摆动周期的减少而增大。但利用SDTE指标及其在拉力设定值中所占的比例来分析这4组实验中追踪误差的数据波动时，4组动态实验的SDTE结果无明显差异(约2%)，这说明在这4个实验中输出拉力的波动程度处于同一水平。但当摆动周期减小到40 s时，如表3所示,在电液力伺服系统在某些时刻的瞬时输出误差会达到8%。在控制器的作用下，液压拉伸力可以很快地调整到正常波动的范围内。并且，这4个实验中的平均跟踪误差为0.3%(表3)，这表明，所设计控制系统的控制精度较好。

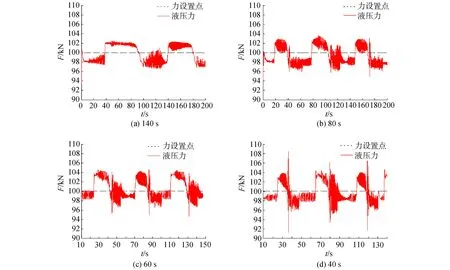
图10 动态拉伸力试验结果Fig.10 Experiment results of dynamic stretching force

5 结论

1)脐带缆的非线性弯曲特性和实际工况下的时变参数，使得脐带缆弯曲端的恒拉力控制存在较大误差。基于自适应线性神经网络模型和LMM算法，使得试验机能够实现脐带缆弯曲端在反复弯曲时达到误差允许范围内的恒拉力控制；

2)在不同频率下，比较参考模型的输出与系统实际输出的误差、比较提出的模型和算法和与传统PID控制器结果，实验结果表明文中所提的控制方案能够有效克服液压参数变化和脐带缆非线性弯曲和拉伸特性带来的干扰，具有更好的恒拉力控制性能；

3)将控制算法应用于静态拉伸实验和动态拉伸实验，结果表明控制系统具有良好的控制精度和鲁棒性能，满足国际主流标准对脐带缆动态恒拉力性能的要求。