A novel DOA estimation algorithm using directional antennas in cylindrical conformal arrays

Xio-feng Go ,Ping Li ,Xin-hong Ho ,*,Guo-lin Li ,Zhi-jie Kong

a Science and Technology on Electromechanical Dynamic Control Laboratory,School of Mechatronical Engineering,Beijing Institute of Technology,Beijing,100081,China

b China Academy of Launch Vehicle Technology,Beijing,100076,China

Keywords:Direction of arrival(DOA)Conformal antenna array Interpolation technique Nested array

ABSTRACT In this paper,a novel direction of arrival(DOA)estimation algorithm using directional antennas in cylindrical conformal arrays(CCAs)is proposed.To eliminate the shadow effect,we divide the CCAs into several subarrays to obtain the complete output vector.Considering the anisotropic radiation pattern of a CCA,which cannot be separated from the manifold matrix,an improved interpolation method is investigated to transform the directional subarray into omnidirectional virtual nested arrays without non-orthogonal perturbation on the noise vector.Then,the cross-correlation matrix(CCM)of the subarrays is used to generate the consecutive co-arrays without redundant elements and eliminate the noise vector.Finally,the full-rank equivalent covariance matrix is constructed using the output of co-arrays,and the unitary estimation of the signal parameters via rotational invariance techniques(ESPRIT)is performed on the equivalent covariance matrix to estimate the DOAs with low computational complexity.Numerical simulations verify the superior performance of the proposed algorithm,especially under a low signal-to-noise ratio(SNR)environment.

1.Introduction

Direction of arrival(DOA)estimation,which is an important field of array signal processing,have a variety of applications such as radar detecting,communication networks,and sonar[1-3].For the DOA estimation problem,researchers have investigated several high resolution methods,such as multiple signal classification(MUSIC)[4],estimation of signal parameters via rotational invariance techniques(ESPRIT)[5],propagator method(PM)[6],tensor algorithm[7,8],and so on.Most DOA algorithm are applied on planar antenna arrays,including rectangular arrays[9],twoparallel arrays[10],L-shaped arrays[11].Unlike conventional planar arrays,the conformal array is an array whose elements are mounted on a smooth curved surface of carrier with good aerodynamic performance,such as spherical conformal array,conical conformal array and cylindrical conformal arrays[12].Except for the regular conformal arrays,some irregular conformal arrays has also been designed to obtain better DOA estimation performance,such as multi-face antenna array with three tilt angles[13].Among various types of conformal array,the cylindrical conformal array has a small radar cross section and wide angle coverage[14,15].Therefore,extensive attention has been paid to cylindrical conformal arrays(CCAs).However,CCAs also has some disadvantages due to their conformal geometry.Affected by the curvature of cylindrical carrier,CCAs are subject to the“shadow effect”,which leads to an incomplete steering vector,containing several zero elements.Hence,the existing DOA estimation method cannot be performed directly on the sparse output of CCAs.Furthermore,because of the metallic curved surface,it is difficult to achieve the omnidirectional antenna element of the CCAs[16].Therefore,the antenna element of CCAs is assumed as a directive antenna in vast majority of literatures,whose radiation responses of each antenna element to the same direction are different.In contrast to the planar array,the radiation pattern of CCAs cannot be separated from the element pattern of the manifold matrix,which means that several search-free subspace methods cannot be used directly.

To solve the above problems,several DOA estimation methods for CCAs have been presented.To eliminate shadow effect,the CCAs is divided into several subarrays to obtain the complete output vector.Then,the MUSIC algorithm is performed on the full-rank output vector of subarray to estimate the angles[17];pseudospectrum searching requires a large number of calculations.To avoid spectral searching,an efficient algorithm for CCAs is presented to estimate the angles with unknown coupling[18].The azimuth angles are obtained by using rank reduction method,which eliminates the coupling coefficients through matrix transformation.To utilize a search-free subspace algorithm on the arbitrary arrays,several techniques such as manifold separation techniques(MST)[19]and array interpolation techniques[20]have been proposed to transform the steering vector of physical arrays into that of uniform linear virtual arrays.The MST can obtain the Vandermonde-structured manifold matrix of virtual arrays,which needs to compute the inverse discrete Fourier transform(IDFT)of the response of the arrays,but the steering vector of CCAs do not satisfy the 2π-periodic property.Unlike the constraint condition of the 2π-periodic discrete set in MST,interpolation techniques can directly transform the real arrays into an arbitrary virtual array by using interpolation matrix.Several novel estimation algorithm for CCAs based on interpolated method has been proposed.A novel algorithm based on interpolated technique has been proposed[21],which transforms the CCAs into a uniform linear virtual array and performs the ESPRIT algorithm on the output of virtual arrays.To estimate the DOAs of more sources,an estimation method for CCAs based on nested arrays is proposed in Ref.[22],which transforms the CCAs into nested arrays and perform MUSIC algorithm to obtain the DOAs.However,these algorithms based on interpolation technique ignore the perturbation of the interpolation matrix on the noise vector.After interpolation,the noise of virtual array is not white Gaussian noise,which may degrade the DOA estimation performance of subspace method.

The maximum estimable number of signals is constrained by the number of available antenna element for CCAs,which is affected by shadow effect.To obtain more degrees of freedom(DOF),several sparse array structures is presented,including minimum redundancy arrays(MRAs)[23],coprime arrays[24],and nested arrays[25].MRAs are put forward to generate the co-array by utilizing the location differences among sensors under the constraint of a difference co-array consisting of consecutive integers.However,the geometry of an MRA,whose sensor location and DOF do not have a closed-form expression,is difficult to design.Unlike MRAs,coprime arrays and nested arrays is proposed to obtain more DOF with a closed-form expression.However,the co-array of coprime array is not a continuous uniform array.In contrast to other sparse arrays,nested arrays can obtainO(N2)DOF consisting of contiguous integers withNsensors.

In this paper,an effective DOA estimation method for directional CCAs is presented to improve the estimation performance.First,we divide the CCAs into several subarrays to obtain the complete output vector,which eliminate the shadow effect.After subarray division,the number of valid antenna elements is reduced to the half of CCAs.By analyzing the non-orthogonality perturbation on the noise vector caused by the interpolated method,we investigate an improved interpolation method to transform the directional subarrays into omnidirectional nested arrays without perturbation.After that,we use the cross-correlation matrix(CCM)of virtual nested arrays instead of the autocorrelation matrix(ACM)to generate the co-arrays without overlapping elements and noise vectors.Then,the full-rank equivalent covariance matrix is constructed with the output of co-arrays.Finally,the unitary ESPRIT algorithm is conducted on the full-rank matrix to obtain the DOAs with low computational complexity.Several simulations and analyses are provided to verify the effectiveness of proposed algorithm,especially under a low signal-to-noise ratio(SNR)environment.

The remainder of this paper is organized as follows:The array configuration and signal model are describes in Section 2.Section 3 presents the main body of proposed method.The computational complexity analyses and simulation results are presented in Section 4.Finally,the paper is concluded in Section 5.

Notation:Matrices are represented boldface uppercase letters,and vectors are represented by the boldface lowercase letters.The superscripts(·)*,(·)T,(·)H,and(·)+represent the conjugate,transpose,complex conjugate transpose and pseudoinverse,respectively.⊙denotes the Khatri-Rao product and‖·‖Frepresents the Frobenius norm.The symbol vec(·)denotes column vectorization andE[·]denotes the expectation.The symbol［.·］stands for finding floor of a decimal number.Furthermore,the notation I and∏represent the identity matrix and the exchange matrix.

2.Array configuration and signal model

Assume there are M directional antennas uniformly mounted in one ring on the surface of a cylinder with radius ofr,composed of a CCA,as shown in Fig.1.

As shown in Fig.2,the origin is defined as the centroid of the antenna array.Consider that the CCAs receiveskfar-field,narrowband signals withNsnapshotssi(t)(i=1，…，k，t=1，…，N)from distinct DOAs,φi(i=1，…，k).TheM×1 output vector at the t-th snapshot is written in matrix form as follows.

where s(t)=[s1(t)，s2(t)，…，sk(t)]Tdenotes thek×1 signal source vector,A(φ)=[a(φ1)，a(φ2)，…，a(φk)]denotes theM×kmanifold matrix of the array.The n(t)=[n1(t)，n2(t)，…，nM(t)]TisM×1 complex Gaussian noise vector with a mean of zero and a variance ofσn2,and is statistically independent of the signals.Since the geometry of CCAs is similar to the circular arrays,we review the manifold of directional circular arrays,and thei-th steering vector of circular array ac(φi)is expressed as follows.

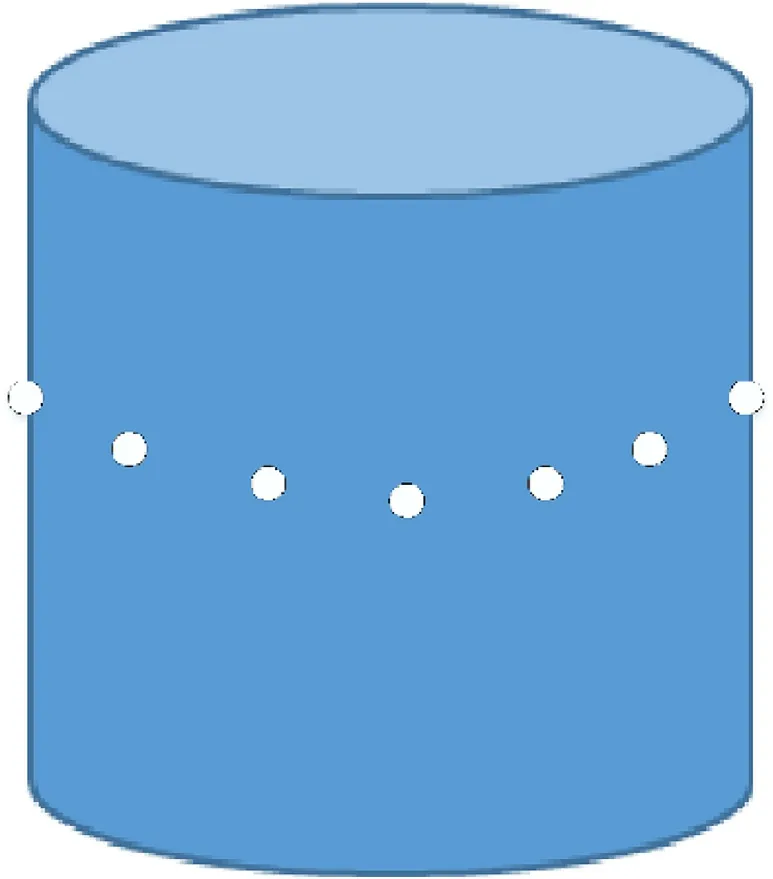
Fig.1.The structure of CCAs.

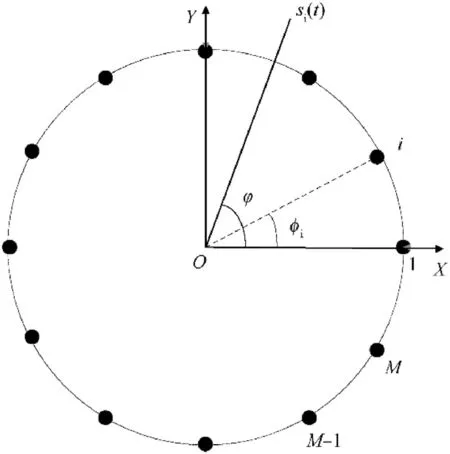
Fig.2.The top view geometry of the CCAS.

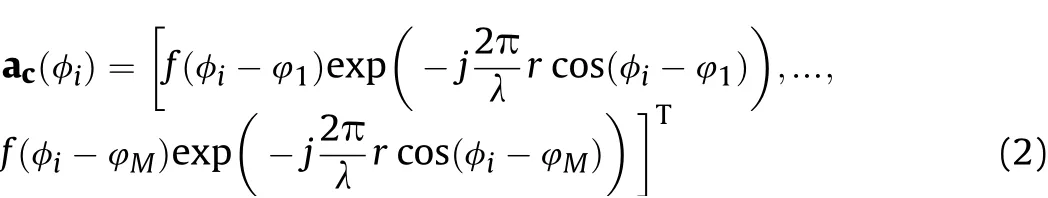
wheref(φi-φl)represents the response ofl-th antenna’s to the angle ofφiandφl=2π(l-1)/Mrepresents the central angle corresponding to thel-th antenna.

Due to the curvature of cylinder,the CCAs are subject to the shadow effect,for which signals emanating from a certain direction may not be received by all the antenna elements,which is different from circular arrays.To depict the shadow effect of CCAs,we define the functionW(φi-φl)as follow.

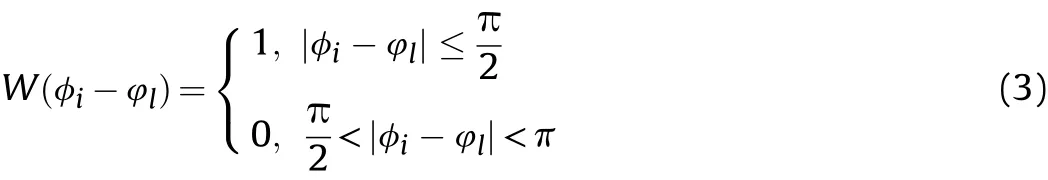
Therefore,the i-th steering vector a(φi)of CCAs is written as

3.The proposed method

3.1.Subarray division and improved nested arrays interpolation

According to the shadow effect of CCAs,the manifold matrix is sparse,which leads to a rank deficiency of covariance matrix of the received signals.The convenient subspace estimation method such as MUSIC and ESPRIT,which need to calculate the eigenvalue decomposition(EVD)operation of covariance matrix,cannot be directly used on the received signals.

To obtain the complete output vector,we divide the CCAs intoNsubarrays.Each subarray is composed ofelements,whererepresents the largest integer not greater thanThe output vector xiof the i-th subarray can be expressed as:

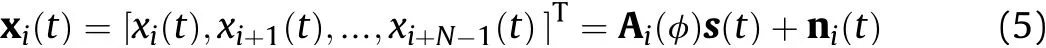
where Ai(φ)denotes the manifold matrix ofi-th subarray,and ni(t)denotes the received noise vector of i-th subarray.

Considering the shadow effect,the angle set of circular sector spanned by the i-th subarray is

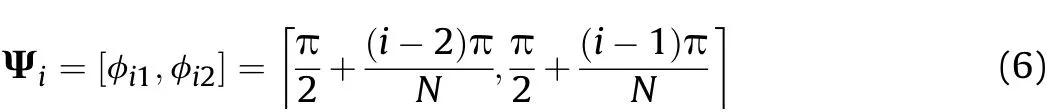
The subarray can also be divided in other ways according to the actual need.After subarray division,the number of valid elements is reduced toN.From Eq.(4),the manifold matrix of CCAs is expressed by the angleφi-φM,which is derived from the local coordinate system of thei-th element.The response of different array element to the same direction is distinct,which cannot be separated from the manifold matrix to simplify calculation.

To address the above problem,we propose an improved interpolation method to transform the directional CCAs to omnidirectional virtual nested arrays.We choose the corresponding circular sector of the sub-array as the interpolated sector and choose the interpolation stepΔφto calculate the manifold vectors of the sectors,lis the interpolation number.The set of i-th sectorΨiand the set of the manifold matrix ofi-th subarrayAi(Ψi)is written as:

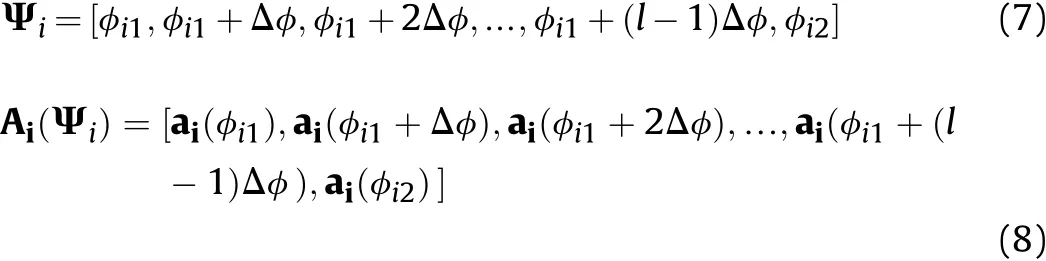
where the number of elements in the setΨiisl,Ai(Ψi)is anN×lmanifold matrix of physical arrays,whose columns are the steering vectors ofΨi.

To mitigate the element loss of CCAs caused by shadow effect,we choose the two-level nested array as the desired virtual array,which consists ofNelements.As shown in Fig.3,the location of the virtual arrays is defined as follow.

wheredis the inter-sensor spacing of inner uniform linear arrays(ULA),which is contained in virtual nested arrays,bis the distance between the first element of virtual arrays and theY-axis,h is the distance betweenX-axis and virtual arrays alongY-axis.

The manifold matrix of virtual nested arrays is defined as Av(φ),and thei-th column vector of Av(φ)is

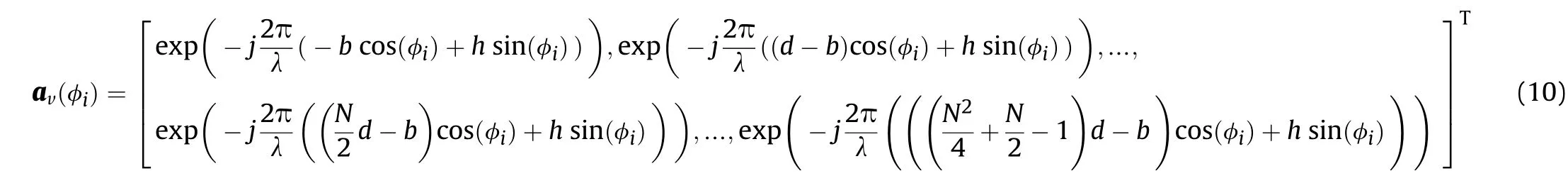
Then,the set of manifold vectors of the virtual nested arrays is computed with the interpolation stepΔφ.

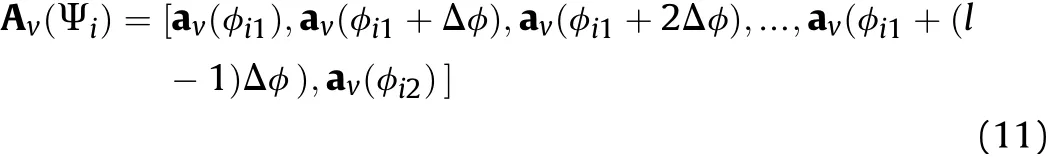
where Av(Ψi)is anN×lmanifold matrix of virtual nested arrays,whose columns are the steering vectors ofΨi.

We review the original interpolation technique in Ref.[18],it utilize interpolation matrix B to map the physical arrays with the desired virtual arrays as follows:

The interpolation matrix is obtained by the least squares method:

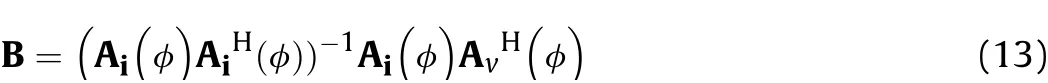
Then the output vectors of the virtual arrays are computed with the interpolation matrix:

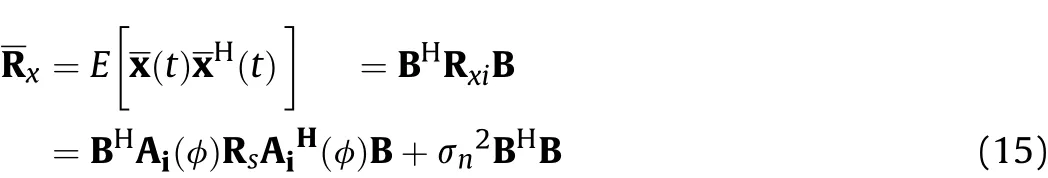
The covariance matrix of the virtual arrays is where Rxi=E[xi(t)xiH(t)]=Ai(φ)RsAiH(φ)+σn2Iis the covariance matrix of the physical arrays,Rs=E[s(t)sH(t)]represents the correlation matrix of the signal sources,andσn2denotes the noise variance.

From Eq.(15),the noise termσn2I in the covariance matrix of real arrays has been transformed intoσn2BHB of virtual arrays.The original interpolated technique only focus on transforming the manifold matrix of physical arrays with the desired virtual arrays,but it ignores the perturbation on the noise vector.After interpolation,the noise vector of different virtual array is not orthogonal with each other.This may degrade the estimation performance of subspace algorithm by amplifying the eigenvalue of the noise subspace.

To reduce the non-orthogonal perturbation of the noise term σn2BHB,we propose an improved interpolation method,which calculate the matrix bB by solving the following optimization problem:

The Lagrangian function is constructed to solve the constraint optimization problem:

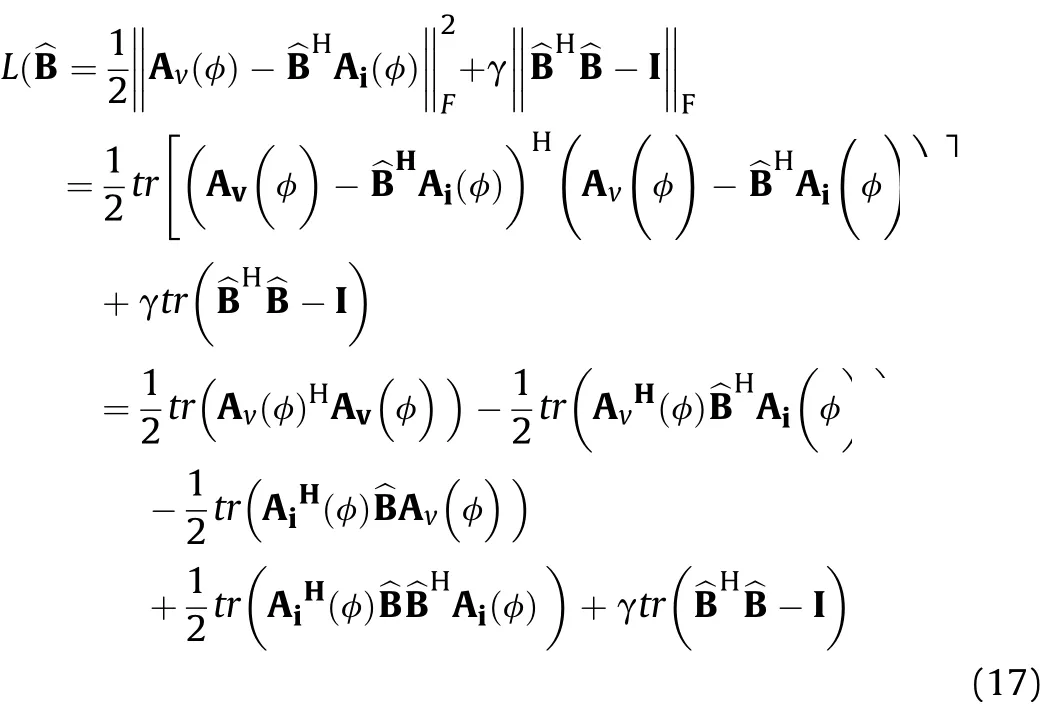
whereγis the Lagrangian coefficient.The conjugate gradient of the Lagrangian function is

Fig.3.The geometry of the virtual arrays.Hollow dot denotes the element of the CCAs,and filled dot denotes the element of virtual nested arrays.

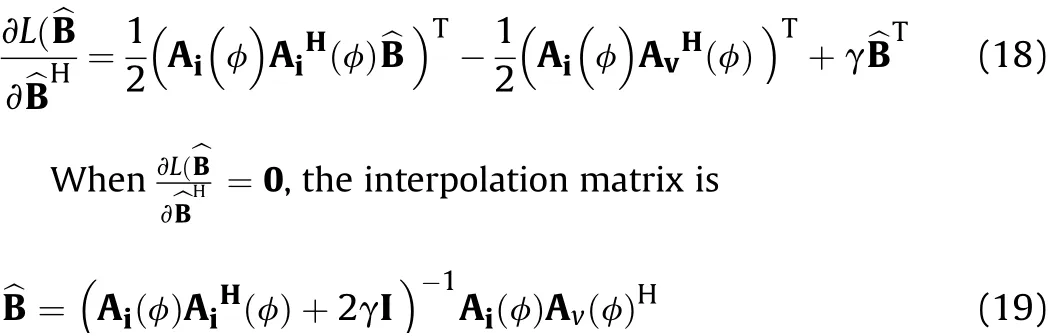
If the ratioεis small enough,the interpolation matrix can be accepted.Otherwise,we need to change the location parameters of the virtual arraysd,bandhto obtain a suitable interpolation matrix.In order to get the suitable location parameters,we define the range of location parameters as follow:

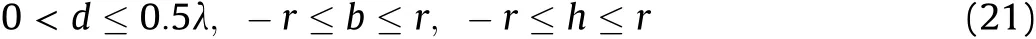
The optimized location of virtual arrays is obtained by solving the following equations with the constraint of the location range:

Then the obtained location parameters are the optimized parameters of our desired virtual arrays.Although the interpolation procedure inevitably increases the computational complexity,the interpolation matrix can be calculated off-line and stored in advance.The effect of the improved interpolation method is evaluated in Section 4.

3.2.Improved Unitary-ESPRIT algorithm for virtual arrays

Divide the virtual arrays into two subarrays,where the first subarray is composed of the firstelements of the nested arrays,and the second subarray is composed of the lastelements of the nested arrays.The output vector of the subarrays are written as:

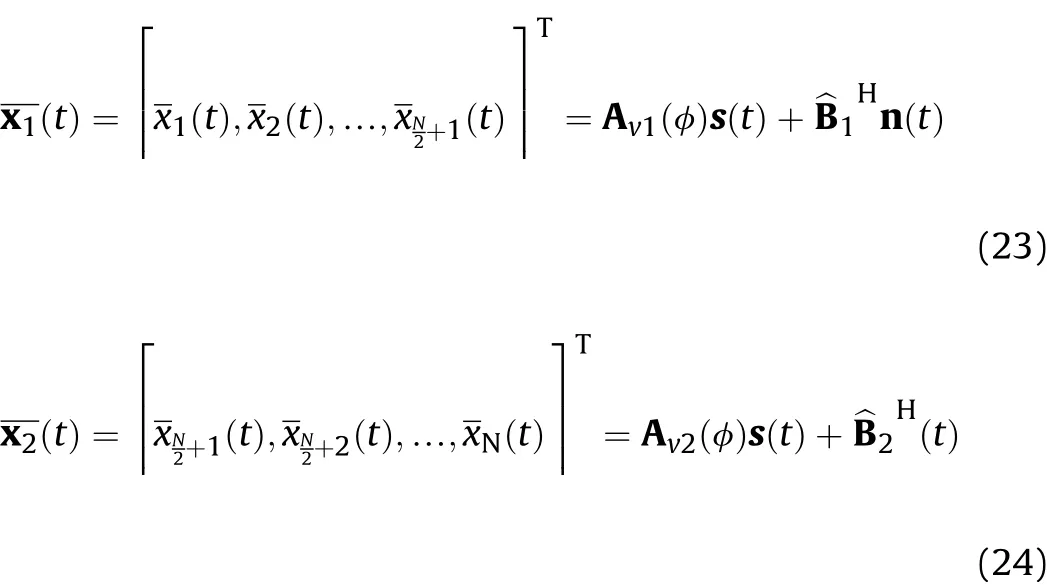
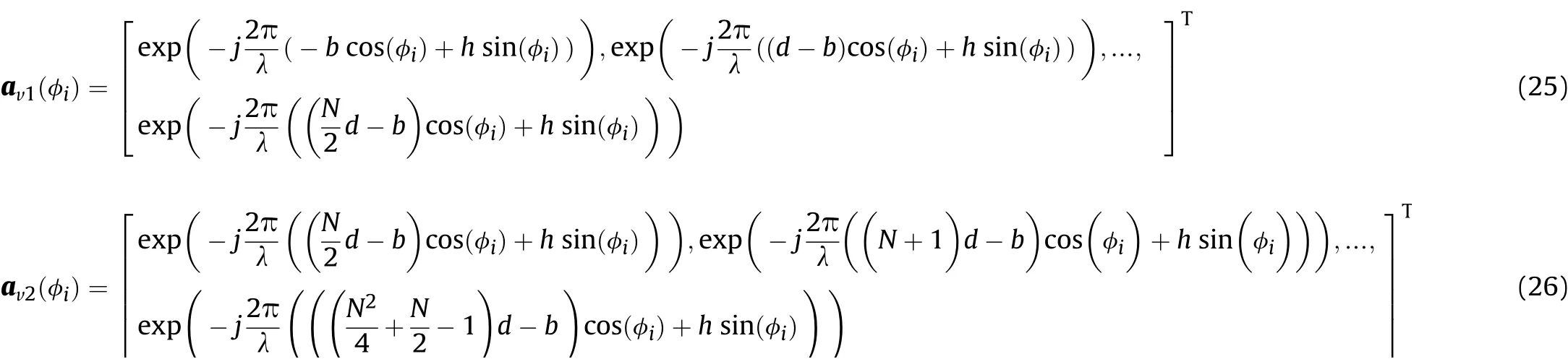
Reversing the output vector of the first sub-array,the vectoris obtained as

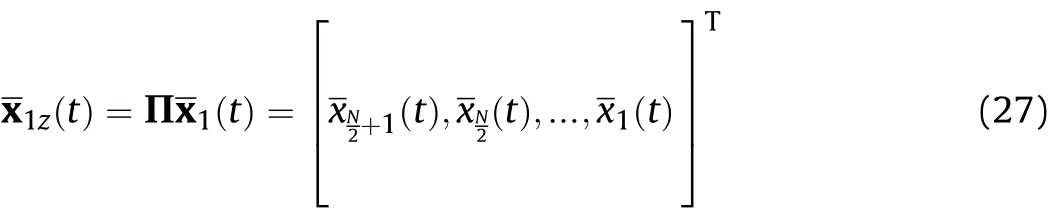
The CCM of different sub-array is calculated as follow.

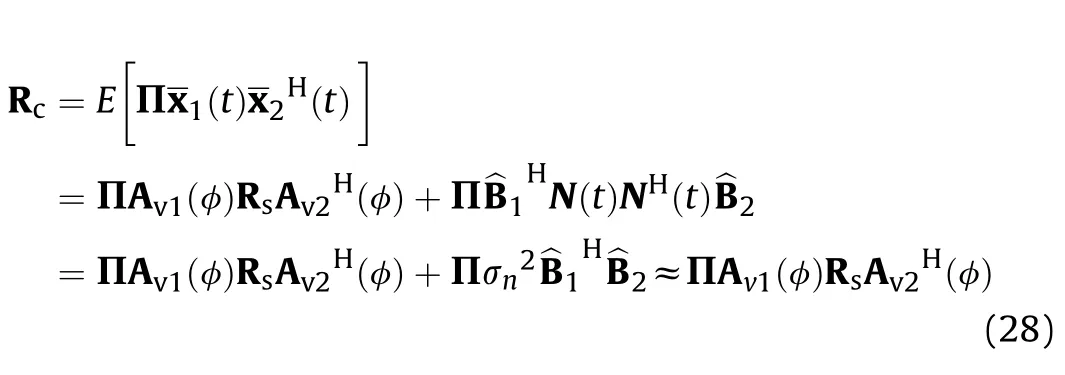
According to Eq.(16),the different row vector ofis almost orthogonal,which means thatThen,the noise vectors of virtual arrays are removed by the cross-correlation operation.By vectorizing the CCM Rc,the vector y is obtained:

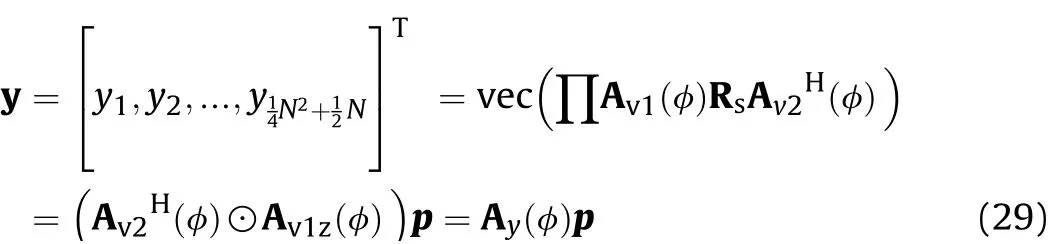
Remarks:As mentioned in Ref.[23],the co-arrays generated by utilizing the autocorrelation matrix(ACM)of output vectors contains some redundant elements.Moreover,the output of the coarrays contains noise vectors,which require an additional operation for their removal.In this paper,we using the CCM instead of the ACM in Eq.(28),which generate the co-arrays without overlapping elements and noise vectors.

According to Eq.(29),the equivalent signal vector p behaves similar to coherent signals,which facilitate the rank deficiency of a covariance matrix.Consider that the covariance matrix of the ULAs is a Toeplitz matrix,the equivalent covariance matrix of the coarrays is reconstructed by using the vector y and its conjugate vector y*.The conjugate vector y*is written as:

The equivalent matrix Ryis expressed as:

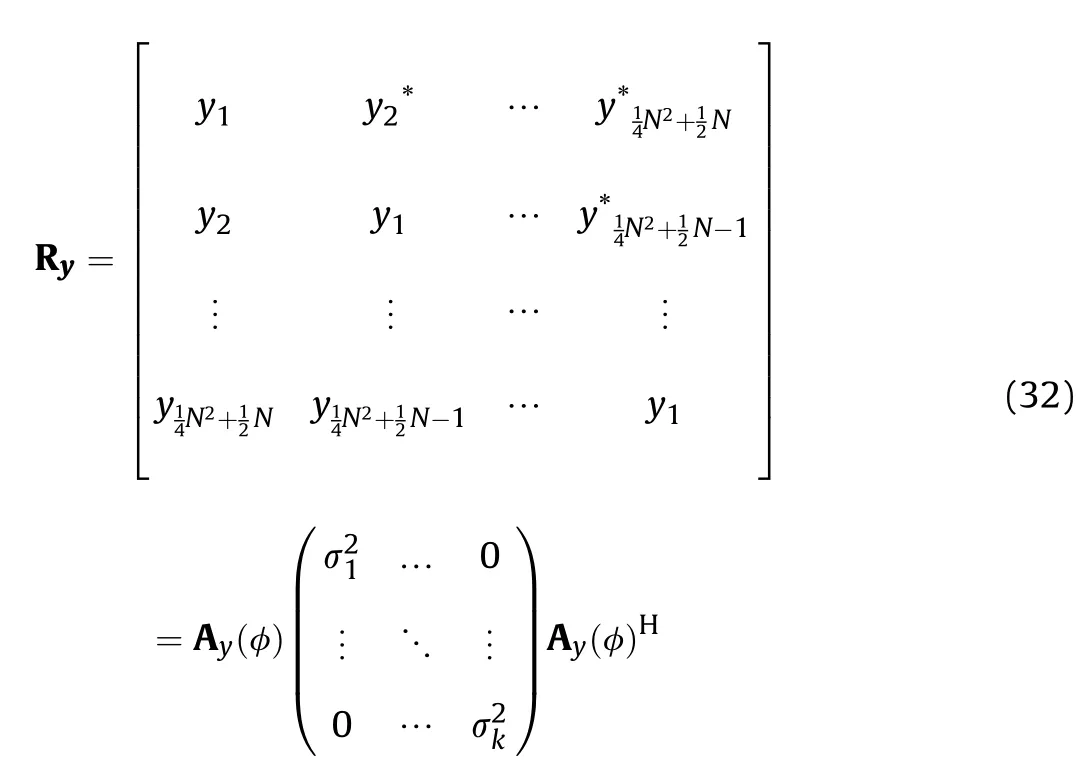
According to Eq.(30),the matrix Ay(φ)is a Vandermonde matrix,which can be seen as the manifold matrix of a ULA.Then the rotational invariance property of Ay(φ)can be written as

The subspace methods such as ESPRIT involves the decomposition of complex matrix,which costs a lot of calculations.Compared with the ESPRIT algorithm,the unitary ESPRIT algorithm,is presented to transform the complex matrix into real-valued matrix through unitary transformation,which can estimate the angles with a lower computational complexity[26].The unitary matrix is defined as:

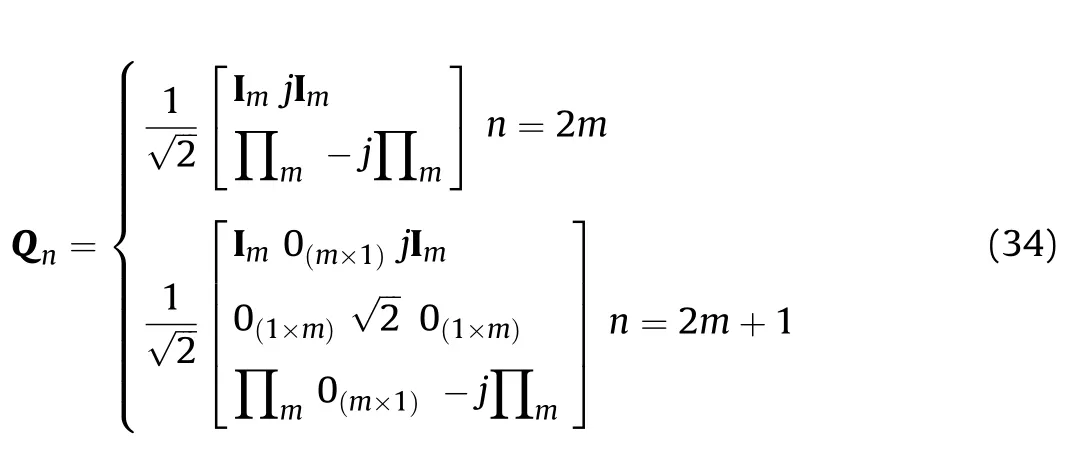
After the transformation with unitary matrix,the real-valued matrix Ry1is expressed as:

After performing eigenvalue decomposition(EVD)on the realvalued matrix Ry1,the rotational invariance property is expressed as:

whereαiis the i-th eigenvalue ofΨy.

3.3.Algorithm implementation

The main steps for implementing the proposed algorithm are summarized as follows:

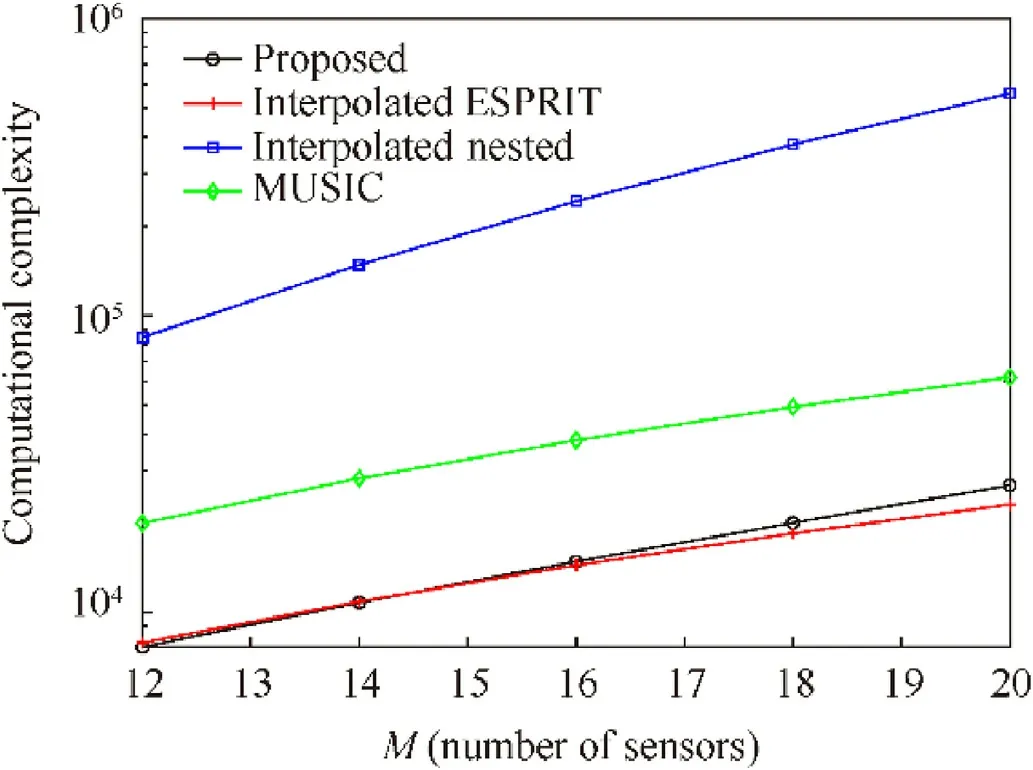
Fig.4.Comparison of complexity versus the number of antennas.

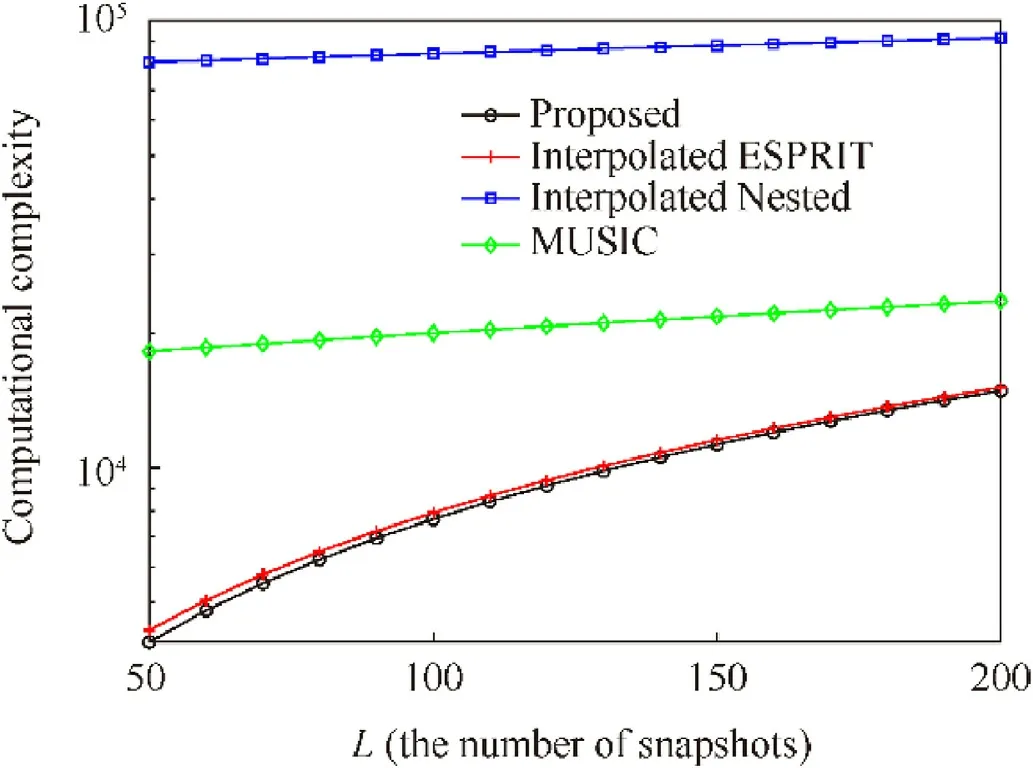
Fig.5.Comparison of complexity versus the number of snapshots.

Step 1:Divide the CCAs into M subarrays,which are composed ofsensors,and the corresponding angle set of circular sector is defined by Eq.(6).

Step 2:For each subarray,construct a virtual nested array ofNelements with optimized location parametersdb,andh,which are obtained via Eq.(22).Then,calculate the interpolation matrix bB via Eq.(19).

Table 1Comparison of computational complexity.

Step 3:Utilizing channel detection to determine the appropriate subarray,calculate the output vectors of the virtual nested arraysby using the interpolation matrixvia Equation(14).

Step 4:The virtual arrays is divided into two subarrays and the CCM Rcis computed with the output of the subarrays via Equation(28).Then,vectorize the matrix Rcto generate the co-arrays via Equation(29).

Step 5:Construct the toeplitz matrix Ryas the equivalent covariance matrix using the output vector y and its conjugate vector y*via Eq.(32).

Step 6:Apply the unitary-ESPRIT algorithm to the covariance matrix Ryto estimate the azimuth anglesbφ.

3.4.Complexity analysis

The main complexity of the algorithm requires the calculation of the CCM,the EVD operation,the pseudo-inverse operation and the least squares method.Because the interpolation matrix could be computed and stored in advance,the interpolation computation should not be considered.The major complexity of the proposed algorithm isO[M2L/2+(M2/16+M/4)3/4+3(M2/16+M/4)k2/4+k3/4].By applying the ESPRIT algorithm to theM/2virtual ULAs,the interpolated ESPRIT algorithm[19]costs approximatelyO[M2L/2+M3/8+3Mk2/2+k3].The interpolated nested MUSIC algorithm[20]and MUSIC algorithm[15],

which involve spectral searching,require operations ofOkM)],whereNrepresents the number of divided subarrays of CCAs,spectral search step is 0.1°.The comparison of complexities by different algorithm are listed in Table 1.

In Fig.4,we plot the computatsional complexity of different algorithms when the number of antennas varies from 12 to 20.Here,the number of snapshots isL=100,and the number of signal sources isk=2.In Fig.5,we compare the computational complexity when the number of snapshots changes from 50 to 200,the number of antennas isM=12.As denoted in Figs.4 and 5,the proposed algorithm costs less calculations than MUSIC and interpolated nested MUSIC.This is due to the unitary transformation,which turns the complex covariance matrix into real-valued matrix.The complexity of proposed algorithm is almost as same as that of the interpolated ESPRIT algorithm.

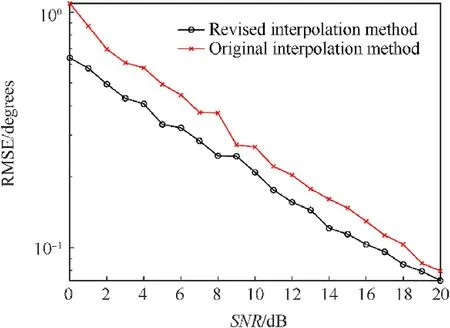
Fig.6.RMSEs versus SNR with different interpolation method.

Fig.7.RMSE versus the SNR,L=100 snapshots.

4.Simulation and analysis

Several numerical simulations are conducted in this section to assess the performance of proposed algorithm.Each CCA is composed of 12 sensors with the radius of 1.28λ,whereλis the wavelength.Two signal sources with the DOAs of 65°and 85°are considered in the simulation,and the antennas are assumed to be identical,with the antenna gain ofIn the following simulations,the root mean square error(RMSE)and the probability of resolution are considered to be the criteria for assessing DOA estimation performance.

The RMSE is defined as follows:

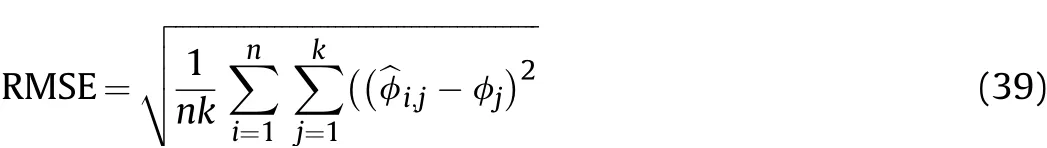
Fig.8.RMSE versus the number of snapshots,SNR=0 dB.

The probability of the resolution is the probability that the angle difference between the estimated angle and the real angle is less than half of the beam width among several Monte-Carlo experiments,which can be expressed as:whereBWdenotes the beam width,bφi，jis the estimated DOA ofj-th signal source at thei-th Monte-Carlo experiment,φjis the DOA of jth signal source,kis the number of signals,and n is the number of Monte-Carlo trials.

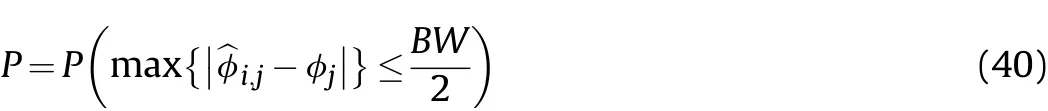
Simulation 1.We verify the effective of the improved interpolation method on DOA estimation.According to Eqs.(5)and(6),the elements of 1-6,corresponding to the angle set of are chosenas the subarray for interpolation,and the optimized location parameter of the virtual arrays is(d，b，h)=(0.2λ，-1.04λ，0.36λ).We compare the proposed algorithm using the original interpolation method[18]via Eq.(13)with the proposed algorithm using the improved interpolation method via Eq.(19).Except for the interpolation method,the other parts of the compared algorithm are as same as our proposed algorithm.The optimized Lagrangian coefficient is defined asγ=1 and the interpolation step isΔφ=0.1°.Fig.6 demonstrates the RMSEs versus SNR withL=100snapshots under 100 Monte-Carlo experiments.It can be seen from Fig.6,the RMSE of the algorithm using the revised interpolation method is lower than that using the original interpolation algorithm,which verifies the effectiveness of revising the interpolation matrix.Therefore,we choose a Lagrangian coefficientγ=1in the following simulations.

Simulation 2.We examine the estimation performance of all algorithms versus SNR.The Cram′er-Rao bound(CRB)[27],the MUSIC algorithms[17],the interpolated ESPRIT algorithm[21],and the interpolated nested algorithm[22]are carried out for comparing with our algorithm.The searching grid for the interpolated nested algorithm and the MUSIC algorithms is 0.1°,and the optimized intersensor spacing of the virtual ULA arrays is 0.23λ,where the error ratio is 1.443×10-4.The subarray and the virtual nested array for proposed algorithm and interpolated nested algorithm is the same as that used in Simulation 1.Fig.7 plots the RMSE versus SNR via 100 Monte-Carlo experiments withL=100snapshots.

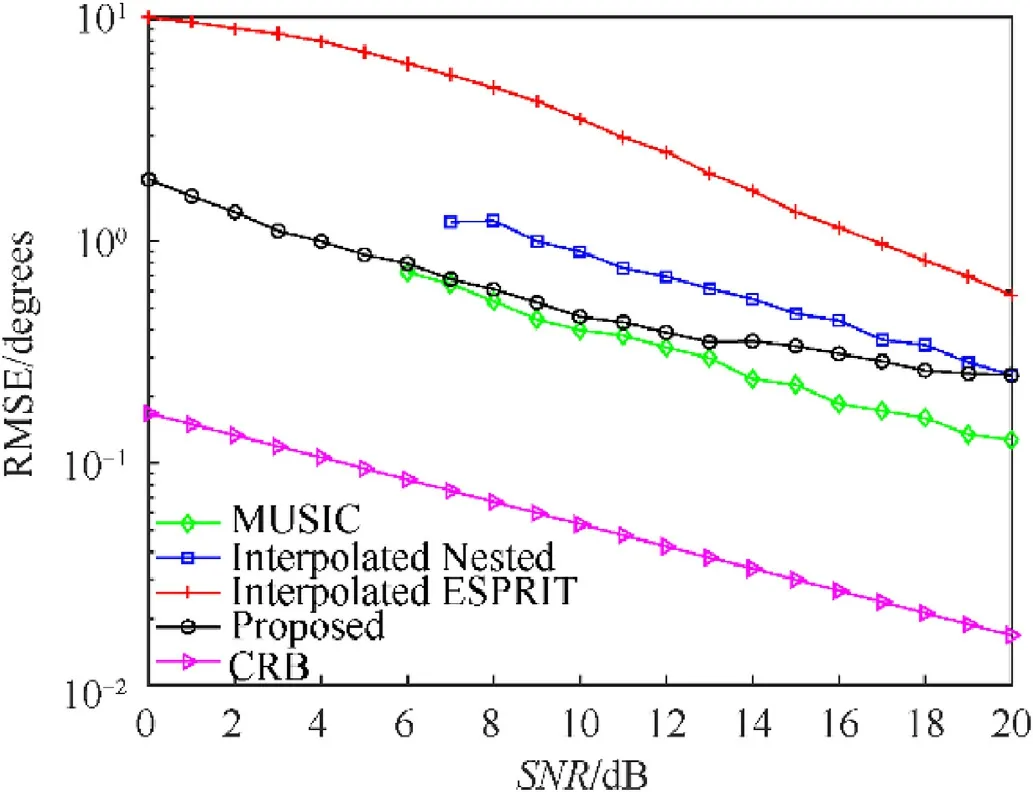
Fig.9.RMSE versus the SNR,L=100 snapshots.

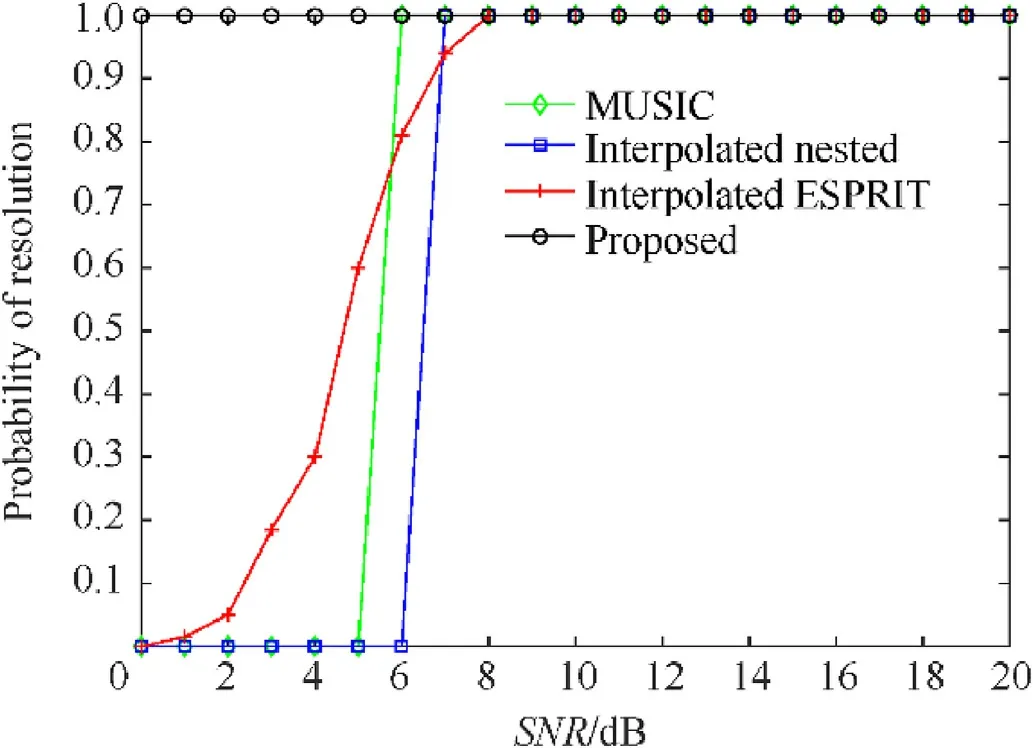
Fig.10.Probability of resolution versus the SNR,L=100 snapshots.

It is seen from Fig.7,the proposed algorithm performs better than the interpolated nested algorithm and the interpolated ESPRIT algorithm.This finding indicates that the proposed algorithm outperforms the interpolated ESPRIT algorithm due to the larger DOF and aperture obtained by interpolating the CCAs into the nested arrays rather the ULAs.Compared with the interpolated nested algorithm,the proposed algorithm enjoys the better performance because it revises the interpolation matrix and utilizes the CCM instead of the ACM which eliminate additive noise.Although the RMSE of proposed algorithm is close to the curve of MUSIC algorithm,our proposed algorithm have lower computational complexity,which avoids spectral searching.

Simulation 3.The estimation performance of all algorithm is investigated in terms of the number of snapshots.The SNRs is set to be 0 dB,and the number of snapshots varies from 50 to 200.The RMSEs versus numbers of snapshots via 100 Monte-Carlo experiments under the SNR of 0 dB and 10 dB are illustrated in Fig.8.

It is seen clearly that our proposed algorithm is superior to other algorithms under low SNR environment.The RMSE of our algorithm is slightly better than MUSIC algorithm under the SNR=0 dB.This is because MUSIC algorithm needs the EVD operation to obtain the noise subspace,which is sensitive to the SNR.On the contrary,our proposed algorithm can estimate the angle precisely under the low-SNR owing to the CCM operation to remove noise vectors.Fig.8 is illustrated that the proposed algorithm is the most efficient one among the tested algorithms under a low-SNR environment.

Simulation 4.The resolution performance of all algorithm is examined by the probability of resolution.Assume two signal sources with the DOAs of 65°and 75°are considered in the simulation.The number of Monte-Carlo experiments is 200.The RMSEs versus SNR is illustrated in Fig.9,and the probability of successful detection versus SNR is given in Fig.10,where the number of snapshots isL=100.

From Fig.9,we can see that the estimation performance for closely spaced objects of proposed algorithm is better than the interpolated nested algorithm and the interpolated ESPRIT algorithm,especially in low SNR environment.Affected by the low SNR environment,the MUSIC algorithm and interpolated nested algorithm fail to estimate the DOAs of closely spaced objects when SNR is lower than 5 dB and 6 dB,respectively.Although the RMSE of MUSIC is slightly better than proposed algorithm when SNR is higher than 10 dB,it fails to obtain the DOAs under low SNR environment.Due to the CCM operation and large aperture of virtual nested arrays,the proposed algorithm can obtains the DOAs of closely spaced objects under low SNR environment.It can be seen from Fig.10,the roposed algorithm’s probability of resolution is 100% when SNR varies from 0 dB to 20 dB.Figs.9 and 10 indicate that the resolution performance of proposed algorithm outperforms than other algorithms.

5.Conclusions

We have proposed a novel algorithm for DOA estimation in CCAs using directional antennas.By dividing the CCAs into several subarrays,the complete output vectors is obtained without zero elements.Then,an improved interpolation method is used to transform the directional sector-shaped subarray into omnidirectional virtual nested arrays without the perturbation of on the noise vector.To obtain more DOF,the CCM of the nested arrays is used to generate the co-arrays without overlapping elements and a noise vector.Then,the full-rank equivalent matrix is constructed with the output of co-arrays,and the unitary ESPRIT algorithm is conducted on the matrix to obtain the angles.Numerical simulations indicate that the proposed algorithm is able to estimate the DOAs more accurately with lower computational complexity than other estimation algorithms,especially under the low-SNR environment.

Funding

This work was supported by the National Natural Science Foundation of China(NSFC)[grant number.61871414].

Declaration of competing interest

The authors declare no conflict of interest.