基于时间-平滑性多目标的机械臂轨迹规划

杨忠瑞，杨昌明，刘 渝，郑克峰，杜承宗

（西华大学 机械工程学院，成都 610039）

0 引言

机械臂广泛应用于焊接、堆垛等多种作业场合。机械臂的轨迹规划是根据作业任务的要求，计算出预期的位移、速度和加速度等与时间有关的运动参数。良好的轨迹规划能保证机械臂末端执行件更好的执行给定轨迹，完成工作任务。但传统的轨迹规划通常只针对单目标进行优化：若为提高机械臂的工作效率，则将时间最短作为优化目标[1]；若希望机械臂运行轨迹平滑[2,3]，则将加加速度的的累加值最小化作为优化目标。文献[4]构建三次样条曲线，通过改变系数的方式使启停时的速度与加速度得到保证，使用SQP算法优化机械臂运行轨迹，采用加权的方法将不同的目标函数统一成单目标优化问题，但三次样条曲线无法对曲线做局部修改，且SQP算法相较于启发式算法，对于复杂问题的计算能力有限。文献[5]构造三次多项式曲线，采用遗传算法对问题进行求解，但只针对机械效率单一目标进行优化，并没有考虑时间减短所带来的振动问题。文献[6]针对轨迹优化时的多目标问题，通过构造7次B样条曲线，使用INSGA-Ⅱ算法求解Pareto解集，7次B样条曲线保证机械臂启停时的速度，加速度，加加速度得到控制，但过高阶次的样条曲线会使计算量大幅增加，严重影响优化速度。文献[7]针对惩罚函数法的不足，提出EGICA算法，通过构造三次多项式曲线完成轨迹优化，对于多目标优化问题，该文献采用的方法是对不同目标函数施加权重，但权重值的分配问题多依赖于经验，容易出现权重值分配不合理的问题。文献[8]针对多目标问题，通过构造5次NURBS曲线，对所有关节同时进行优化，求得Pareto解集，但本文并未就时间控制点反求时所需要的边界条件进行讨论。

本文在上述研究成果的基础上，引入BOEHM节点插值算法对B样条曲线的表达式进行简化，在降低计算量的同时也便于MATLAB运算求解，同时对反求时间控制点时所需要的边界条件进行讨论。本文兼顾效率和平稳性的运行需求，建立了多目标优化模型，并采用NSGA-Ⅱ算法优化求解。仿真表明，基于五次NURBS曲线生成的速度、加速度与加加速度轨迹曲线光滑且连续，能够保证机械臂运行平稳，减少冲击与振动。本文研究为解决实际工程问题提供了一种有效参考。

1 多目标最优轨迹的问题描述

实际生产中，通常寻求时间最短的轨迹，但这会引起速度、加速度、加加速度的增大，导致机械臂磨损加快、振动加剧，不利于机械臂的可靠平稳运行。因此，在提高机械臂工作效率的同时又能兼顾其平滑性的情况下，进行多目标最佳轨迹规划具有实际意义。

轨迹规划的主要任务在于根据给定的路径点获得期望的运动轨迹。在关节空间中，路径点序列可表示为Pi,j（qi,j，tj），其中i=1，2，…，N，j=1，2，…，m，N为机械臂关节数，m为路径点数，qi,j表示机械臂第i个关节在时间节点tj处的角度值。

多目标最优轨迹规划中，如为了提升作业效率与提高机械臂运行平滑性，可将优化目标定义如下：

式中，tj为待优化变量，obj1为机械臂运行总用时间，反映了机械臂的运行效率；obj2为机械臂加加速度累加值，反映了机械臂运行过程中的平滑性。为了保证机械臂平稳运行，还需规定在机械臂运行过程中的最大速度，加速度，加加速度，使其满足：

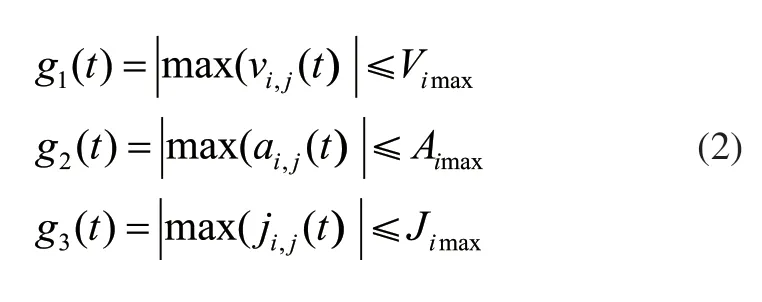
2 基于B样条插值的轨迹构造

现轨迹规划相关文献中，关于B样条曲线的表达式多基于de Boor-Cox公式递归得到，但由该递归公式得到的表达式对于B样条曲线的表示较为复杂，计算量庞大，不易用矩阵形式进行表示且不利于用MATLAB求解计算。因此，本文引入Boehm节点插值算法将B样条曲线的表达式转换成矩阵形式进行表示[9]，使其在降低计算量的同时也便于MATLAB运算求解。Boehm在deBoor-Cox算法的基础上提出，当在t*∈[ti，ti+1）插入一个节点m时，对修正后的控制点引入新的递归公式，通过对该递归公式进行递归，可以得到B样条曲线基函数的矩阵表达形式。由于B样条曲线型执点权重的确定缺乏依据，所以为简化样条表达式，将各控制点的权重均设为1，则5次B样条曲线的第i段曲线的表达式简化如下：

矩阵当中的值ni,j可由B K Choi给出的递归公式得到，本文给出n1，1，…，n1，6的值以供参考：

式中，b，c，…，j为B样条曲线其中一段样条支撑节点的节点值，将对应的节点值代入公式即得到该段5次B样条曲线的基函数，即5次B样条曲线表达式得以确定。

对于包含n个型值点的K次B样条曲线，节点首尾应当具有K次的重复度以保证样条曲线首尾值与控制曲线首尾相重合，即a0=a1=…=aK-1=0，aK+n-2=aK+n-1=…=a2K+n-2=1，其余节点基于所生成的时间tj采用累计弦长法确定，如式6所示，其中f=k,k+1,…,k+n-2：

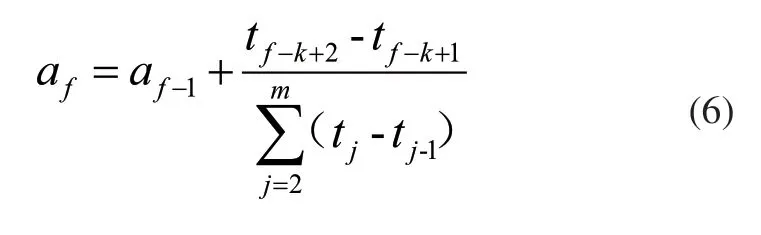
为使轨迹经过指定路径点，还需对B样条曲线的控制点进行反求，控制点分为角度控制点与时间控制点。经过n个指定路径点可以确定n个方程，对于含n个型值点的K次B样条曲线，需要K+n-1个控制点才能实现对样条曲线的完全控制，故此时还需补充K-1个边界条件才能确定所有控制点，为了避免机械臂产生刚性冲击、延长机械臂使用寿命，通常将机械臂起停时的速度与加速度作为边界条件，即：

式(7)中，vs，ve为机械臂关节起停时的速度值，as，ae为机械臂关节起停时的加速度值。通过式(8)的首尾两行可以实现对机械臂起停时速度与加速度的控制：

通过式(8)可以反求出所有角度控制点的值，从而角度控制点得以确定，式中qi为角度控制点值，Qi为型值点值。

为实现对B样条曲线的完全控制，还需将本次优化生成的时间信息ti进行反算转换为与角度控制点信息相对应的时间控制点信息Ti。同样，对于含n个型值点的K次B样条曲线，还需要补充K-1个方程才能确定所有控制点，其方程如式(9)所示，但式中C1、C2、C3、C4的值难以确定，故对时间控制点的反算存在困难。经实验发现，对时间的一阶与二阶导数施加不同边界条件会对t-u曲线斜率产生较大影响，且该曲线斜率与关节速度、加速度、加加速度曲线存在映射关系。速度、加速度、加加速度的突变会引起机械臂振动，影响轨迹精度及机械臂寿命，所以应期望t-u曲线的斜率变化趋于常数，并且强调t-u曲线必须单调递增。一般情况下，可根据经验确定C1、C2、C3、C4的初始值，为避免优化变量过多造成产生优化不收敛的情况，先采用C1、C2、C3、C4的初始值对时间进行优化，当时间种群趋于稳定后，再将常数C1、C2、C3、C4与时间同步优化，于是时间控制点信息反求表达如式(9)所示。

4 NSGA-Ⅱ算法

NSGA-Ⅱ算法是一种基于遗传算法，针对解决多目标优化问题发展而来的一种改进遗传算法。与传统遗传算法所得到的精确解不同，通过NSGA-Ⅱ算法得到的解不是传统意义上的一个解，而是一组解集，称为Pareto最优解或非支配解集。该解集并无优劣之分，其特点是对于该解集中的某一个解在其所对应的至少某一项目标函数上，该解集中的其他解均劣于它。该算法通过引入精英策略，根据种群的等级制度与拥挤度信息进行排序与淘汰，从而在保证算法寻优性能的基础上降低运算次数。Pareto解在保证解的多样性同时，可以直观了解不同目标函数之间的制约强度，为寻找实际工程最优解时不同目标函数间权重的确定提供了依据。本文结合该优化算法将效率与平滑性作为优化目标，将型值点Pi,j（tj）的值与时间控制点补充方程的值C1、C2、C3、C4作为优化变量进行求解。

根据给定型值点的个数，生成初始规模为N关于时间控制点的初代种群，种群中的每个个体均为m+4维向量。初代种群的性能不仅对算法的收敛速度有较大影响，对Pareto解集的解密度也有较大影响，因此提高初代种群的素质是极有必要的。本文充分利用给定路径点的信息，采用式(10)生成初始待优化变量tj：

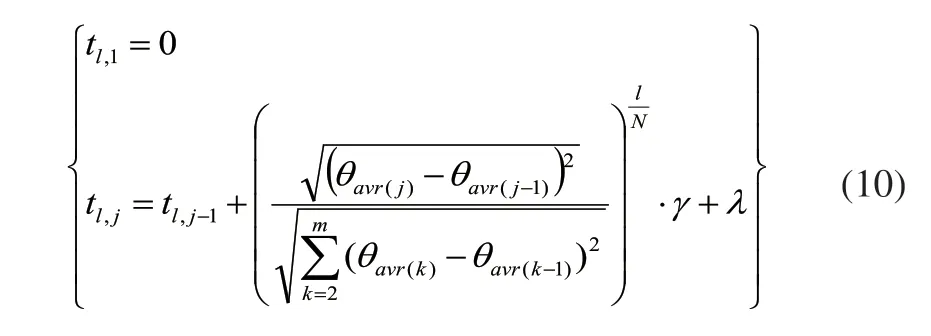
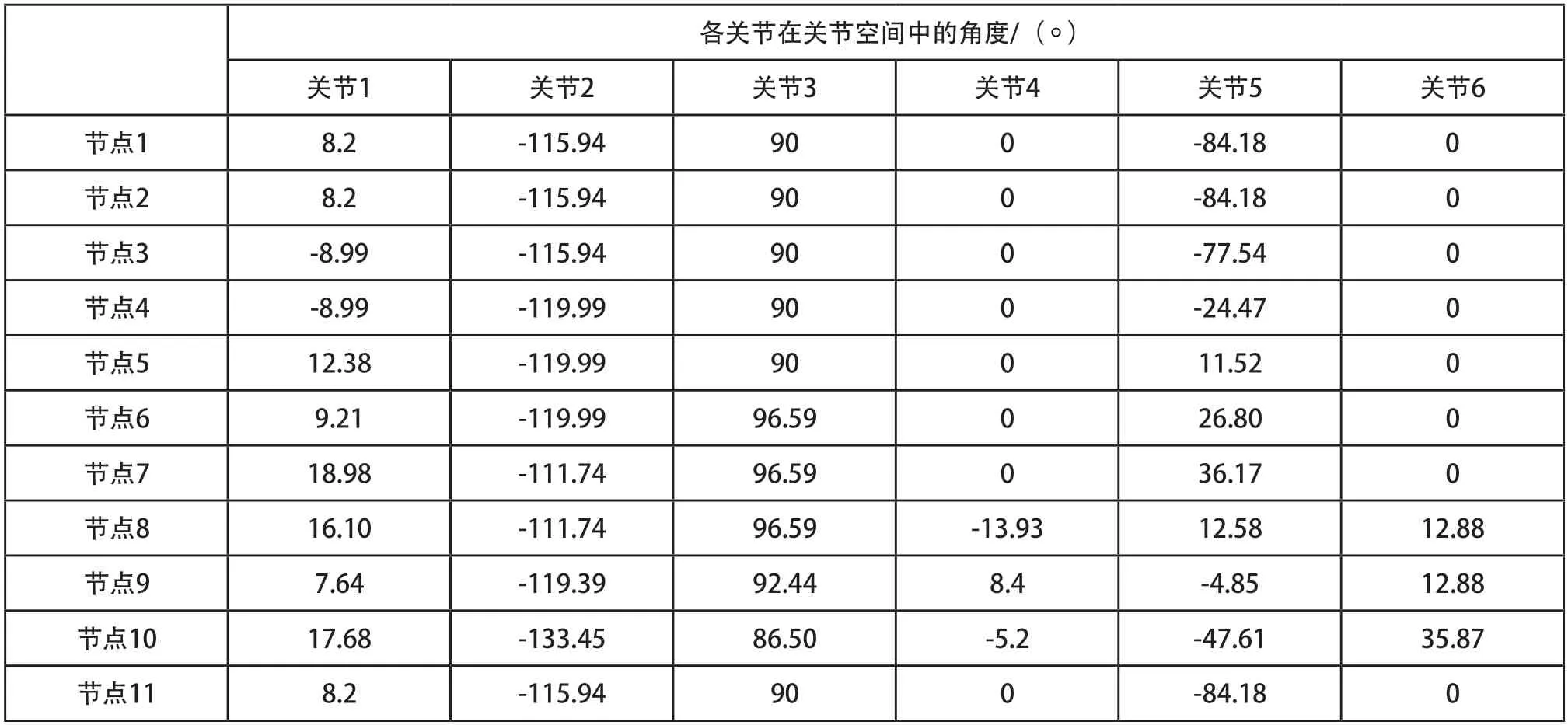
表1 关节位置序列

式中，l=1，2，…，N；j=2，3，…，m，γ是tj的步长系数，λ是tj的最小步长，θavr(j)为机械臂第j个型执点各关节臂所对应关节角的平均值，当生成的种群不满足优化的约束条件时，可通过该改变γ与λ调整初始种群数值分布情况。

2）计算种群个体的等级信息与拥挤度信。

3）对种群进行遗传与变异，产生新的子代个体。种群规模为N的父代种群Rt生成的子代种群Ct，其规模约为2N。

4）将父代种群与子代种群合并成规模约为3N的新种群并重新计算种群中个体的等级信息与拥挤度信息，对不满足约束条件的个体进行惩罚降级处理，以保证迭代结束时等级信息为1的个体能满足优化模型的约束条件。根据等级信息与拥挤度信息对种群进行排序，根据精英策略的要求，将排序后序号小于N的个体保留作为新父代群体，其余个体淘汰。

5）迭代次数增加，若此时迭代次数小于许用迭代次数，则重复步骤2）～4），若迭代次数大于许用迭代次数，进入6）。

6）将迭代后种群中等级信息为1的个体输出，得到Pareto最优解。

5 仿真测试

5.1 仿真条件与约束设置

本次仿真测试数据由某生产现场一台kuka六自由度机械臂提供。机械臂在运行过程中需通过11个型值点，其值如表1所示，机械臂的运动学约束如表2所示。关节轨迹曲线由五次NURBS曲线构造，运行起停速度与加速度均约束为0。

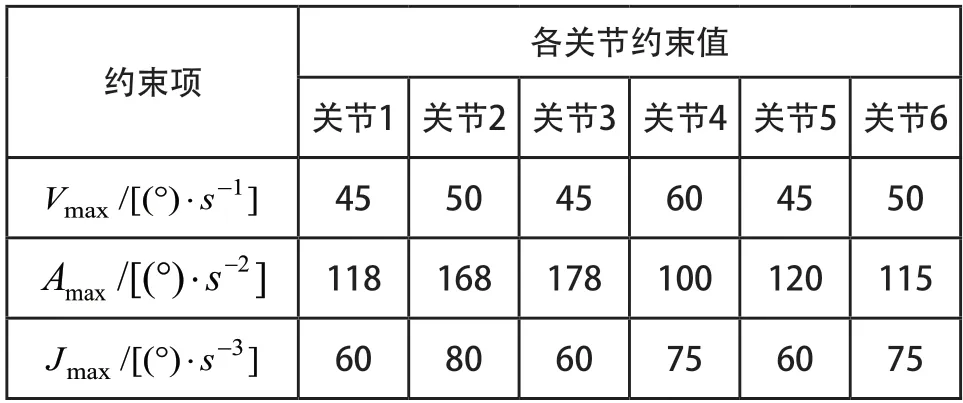
表2 运动学约束

5.2 测试结果及对比

对速度、加速度和加加速度施加约束，以平滑性和效率作为优化目标，该问题的Pareto解如图1所示。

图1 Pareto最优解分布

由图1可知，机械臂的运行效率与平滑性相互制约，Pareto解曲线的斜率反映了不同目标函数之间的制约强度。本次优化采用min-max标准化归一法，权重函数为：

式中sj为权重系数，其值根据具体实际工程问题的要求决定，本文取s1=0.6，s2=0.4，通过归一加权处理得到的工程最优解对应的目标函数obj1=30.68s，obj2=343.73°·s-3。规划得到的时间向量为t=[0，4.4172，6.4488，9.2134 11.4936，14.6279，16.8939，19.9049，22.4107，25.7696，30.6811]，C1=6.0150，C2=5.7638，C3=6.1144，C4=5.916。工程最优解中机械臂各关节的速度、加速度、加加速度曲线如图2所示。

图2 各关节位移、速度、加速度、加加速度曲线

由图2可知，基于五次NURBS曲线生成轨迹的速度、加速度与加加速度曲线光滑且连续，这可以保证机械臂在运行过程中不会产生冲击，运行更为平稳。通过对五次均匀B样条曲线增加边界条件可以对机械臂启停时刻的关节速度与加速度进行约束，避免了机械臂启停时产生刚性振动与冲击。基于NSGA-II算法进行优化可以得到可视性更强且满足约束条件的解，对解决实际工程问题提供了方便。与文献[4,5,7]相比，可以看出本文得到的Pareto解可以为目标函数的权重系数的确定提供依据，且可对轨迹进行局部更改；与文献[8]相比，本文对时间边界条件进行优化，进一步提升轨迹性能；与文献[3]相比，在保证轨迹性能的情况下，极大的降低了运算次数。

6 结语

本文采用5次非均匀B样条曲线在关节空间中构造6R型机械臂关节轨迹，在保证起停速度、加速度为0的同时，轨迹的速度、加速度、加加速度曲线也光滑且连续。通过引入Boehm节点法对deBoor-Cox递归公式进行简化，降低了运算难度，方便求解。对时间控制点反求时所补充的边界条件进行同步优化，可获得性能更好轨迹曲线。引入NSGA-II优化算法以机械臂的运行效率及降低振动、冲击为目标，对时间序列进行优化得到满足运动学约束的Pareto解集。对6R机械臂的仿真实验结果表明该优化在实际工程问题中具备有效性。在后续的研究中，将针对遗传算法搜索能力不足的问题，通过结合其他启发式算法，进一步提高优化性能。