基于ARIMA模型的我国疟疾的研究与应用

马 霞,王晓佳

（太原工业学院理学系，山西太原 030008）

疟疾是一种虫媒传染病，通过蚊虫叮咬传播，症状主要为贫血和脾肿大后全身发冷、发热、出汗等。疟疾是我国法定传染病之一，预测疟疾的发病情况对于我国的医疗卫生事业有重要意义。ARI⁃MA模型是Box和Jenkins[1]在20世纪70年代初提出的著名的预测方法。国内外对ARIMA的应用十分广泛，樊雯婧[2]应用ARIMA模型拟合1991−2011年合肥市每月疟疾发病率，并预测2012年各月份疟疾发病率，取得了较好的预测效果。肖丹[3]采用贝叶斯统计模型研究了索马里的恶性疟疾发病情况。郑慧敏[4]研究了ARIMA模型在深圳市法定传染病发病趋势预测的应用。戴琳琳[5]研究了基于模型的青岛市GDP的预测分析，为青岛市经济决策提供重要的依据。近几年，国内外学者综合考虑了序列的趋势变化、周期差异等，将ARIMA模型应用于GDP的预测当中，结果显示模型预测效果良好[6−7]。为减小误差，提高预测精度，很多学者通常选择采用多个模型组合的方法或者将单一模型进行修正，从而提高预测精度[8−9]。运用自回归求和移动平均(模型)对全国疟疾各月发病趋势进行预测，并探讨模型的准确性，同时其传染病预测模型的研究提供参考，为疟疾的防控工作提供依据。

ARIMA(p，d，q)称为差分自回归移动平均模型，AR是自回归，p是自回归项。MA是移动平均，q是移动平均项的数目，d是时间序列稳定时的差分数目。ARIMA模型的表达式[1]为：

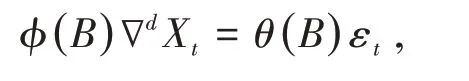
其中Xt表示在t时刻的一个时间序列，εt表示一个白噪声(零均值，方差是一个常数)，d表示差分阶数，B表示后移算子，即BXt=Xt−1，∇=1 −B，φ(B)表示自回归算子，自回归系数多项式为：

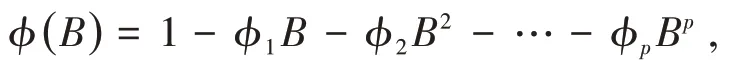
θ(B)表示移动平均算子，移动平均系数多项式为：

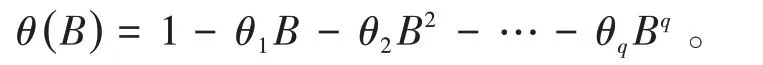
若模型包含季节性的成分，还应当考虑带季节性的SARIMA（p，d，q）（P，D，Q）S乘积模型，其中P表示季节周期的自回归的阶数，D表示差分次数，D表示滑动平均的阶数，s表示季节周期。其中φ(B)∇dXt表示相同周期内各周期点之间的相互关系，φ(B)∇D则表示的是不同周期中对应时点上的相互关系。SARIMA（p，d，q）（P，D，Q）S乘积模型的数学表达式为：

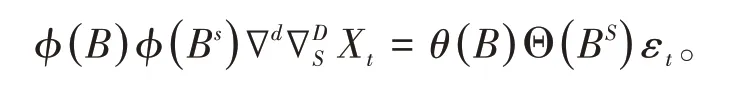
1 数据的预处理

选取了全国2012−2019年各月疟疾发病人数，数据如表1（数据来源于中国疾病控制中心网站[10]），表中数据可以看出全国疟疾患病总人数整体是逐年递减的，2013年患病总数偏高，之后呈波浪式下降趋势。

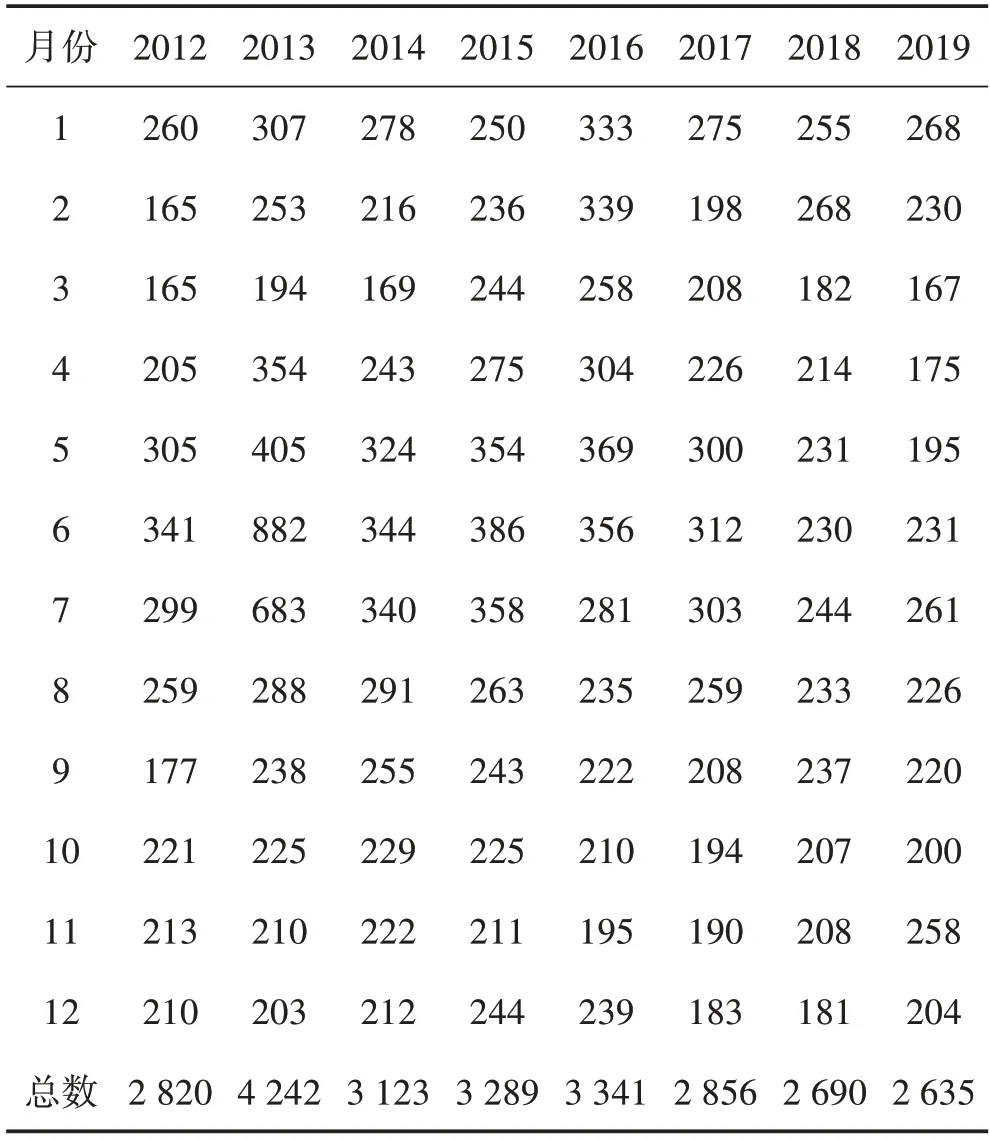
表1 全国2012-2019各月度疟疾发病人数/例

2 模型的建立

2.1 模型的检验

根据2012−2019年全国疟疾的发病数制作时序图(图1)，可看出2013年的数据明显高于其他年份，疟疾的发病情况具有明显的季节性，序列是非平稳的，因此，需要进行一阶季节性差分，去除季节的影响，最终获得平稳序列（图2）。选用图形检测法和单位根检验方法检验平稳性。由表2可知，ADF单位根检验的统计量为−6.219 312，该结果明显小于各显著水平临界值，符合平稳性条件，即该序列不存在单位根，发病数Yt是平稳的，因此，ARIMA（p，d，q）中的d=0，故可以构建ARIMA（p，q）模型。

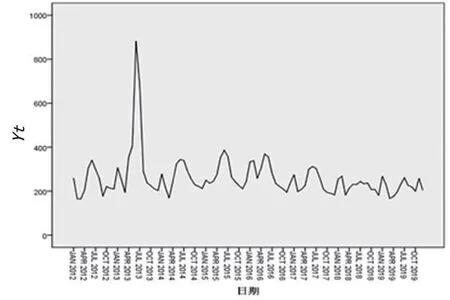
图1 2012-2019年全国疟疾发病数序列图

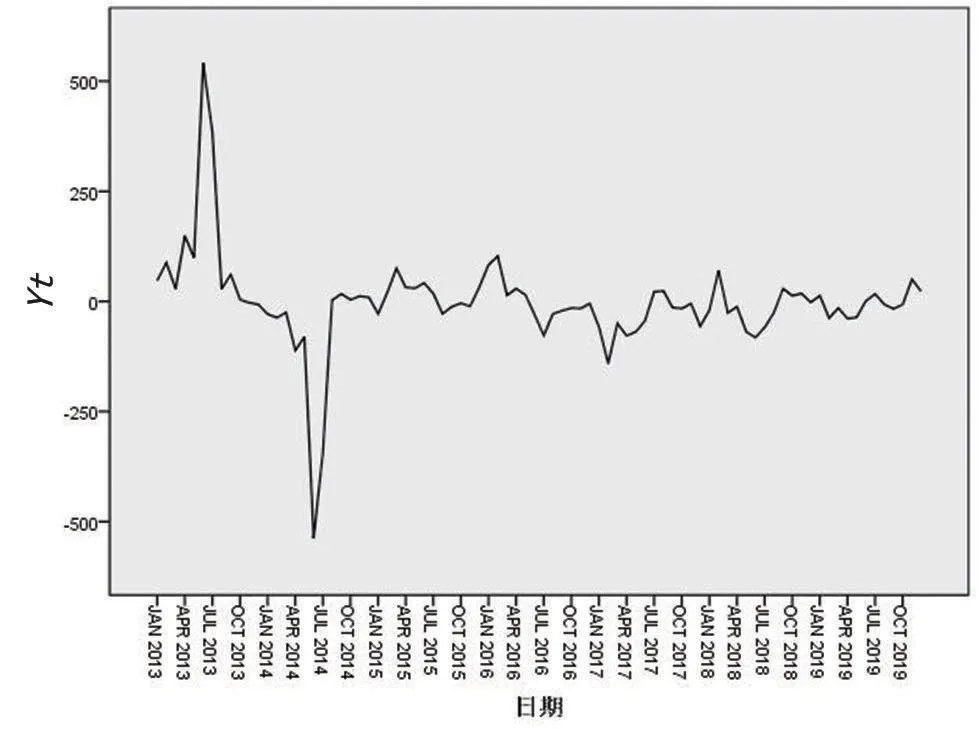
图2 经处理后的疟疾月度发病数序列图

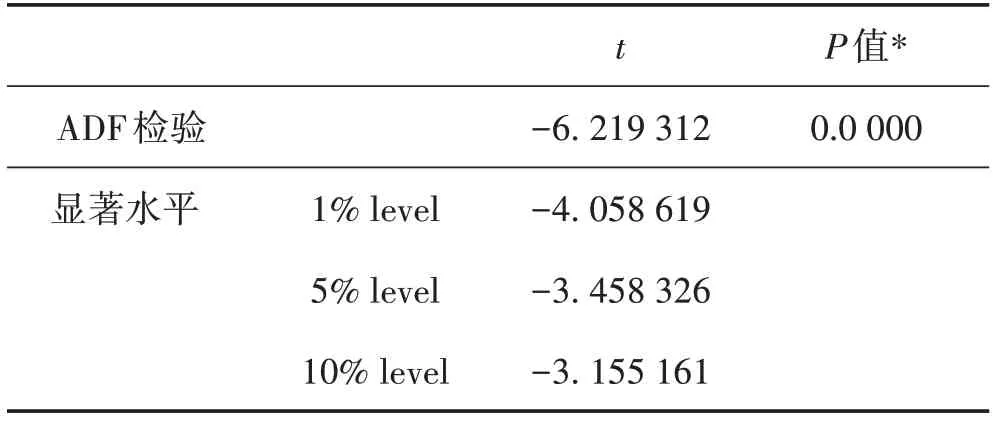
表2 处理后疟疾月度发病数序列的ADF单位根检验结果

2.2 模型的识别与参数估计

根据序列的平稳性和季节特征，通过观察序列自相关系数图和偏相关系数图（图3和图4），ACF在1后随参数P的增大而突然减小，PACF在2后随参数P的增大而突然减小，从而初步确定连续模型为ARI⁃MA(1，0，2)。通过观测季节自相关系数图和偏相关系数图（图5和图6），季节模型的参数P和Q，一般不超过二阶，将0，1，2分别代入从低阶到高阶进行调试，根据残差分析得出模型ARIMA(1，0，2)(0，1，1)12、模型ARIMA(1，0，2)(1，1，0)12和模型ARIMA(2，0，2)(0，1，1)12为备选模型。BIC值最小的是最优预测模型，显示拟合优度最好的是ARIMA(1，0，2)(0，1，1)12(如表3)。

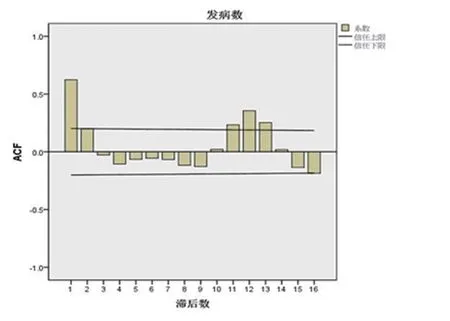
图3 0阶差分自相关图

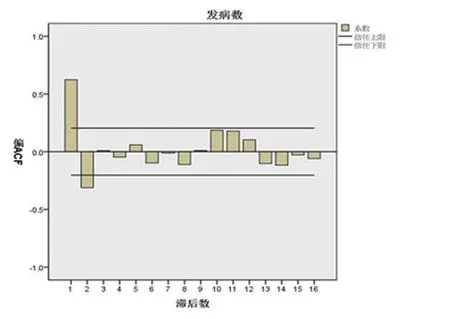
图4 0阶差分偏自相关图

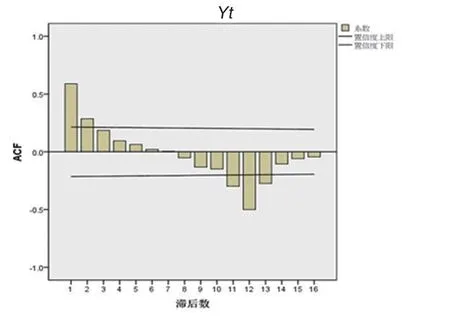
图5 1阶差分自相关图

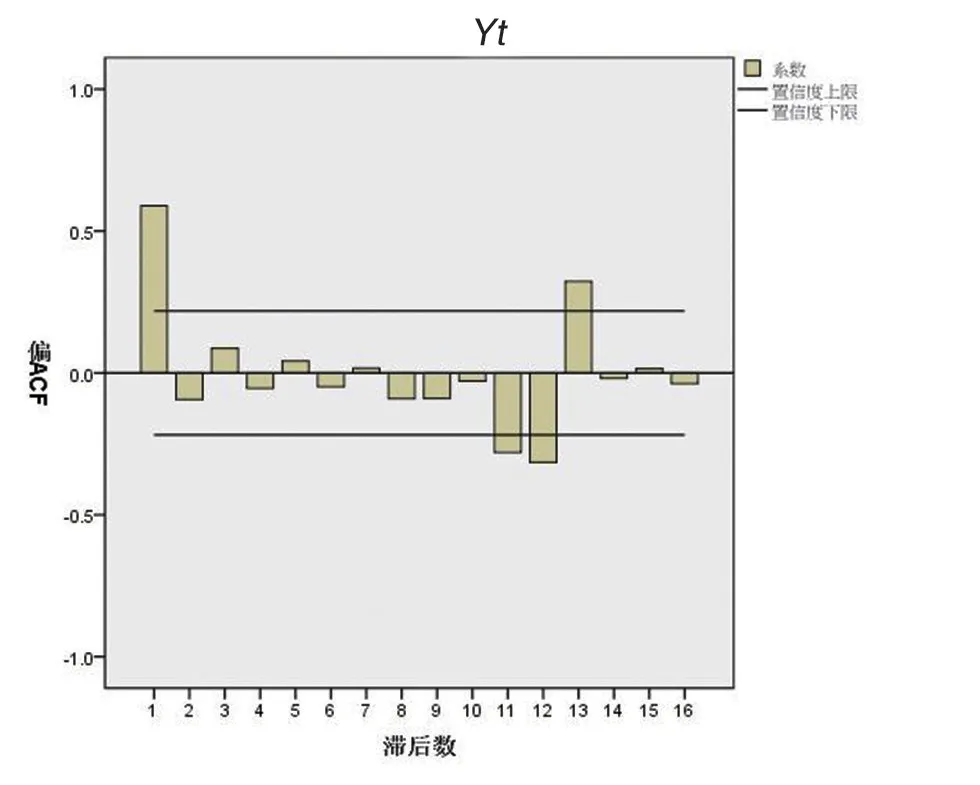
图6 1阶差分偏自相关图

表3 备选模型参数比较

2.3 模型的诊断

通过验证残差序列，判断模型ARIMA(1，0，2)(0，1，1)12的适用性。由AFC图和PACF图所给信息，根据残噪声检验图(图7)可知相关系数均分布在95%的置信区间内，判断ARIMA(1，0，2)(0，1，1)12模型是适用的。

图7 残噪声检验图

2.4 模型的预测

用ARIMA(1，0，2)(0，1，1)12对2012−2019年全国疟疾各月发病人数进行拟合，得出其拟合值与疟疾实际值进行对比如图8所示。可知疟疾的发病数均在拟合值的置信区间内，通过该模型预测出2020年1−12月全国疟疾发病的人数如表4。把每个月的数据进行累加求和便可得2020年疟疾的发病数为2 148。虽然预测的模型预测的数据和实际值不完全吻合，但是从表5可知，预测值与真实值的相对误差很小。进一步说明模型的拟合效果较好，因此，该可以用来预测我国疟疾的流行发病情况。

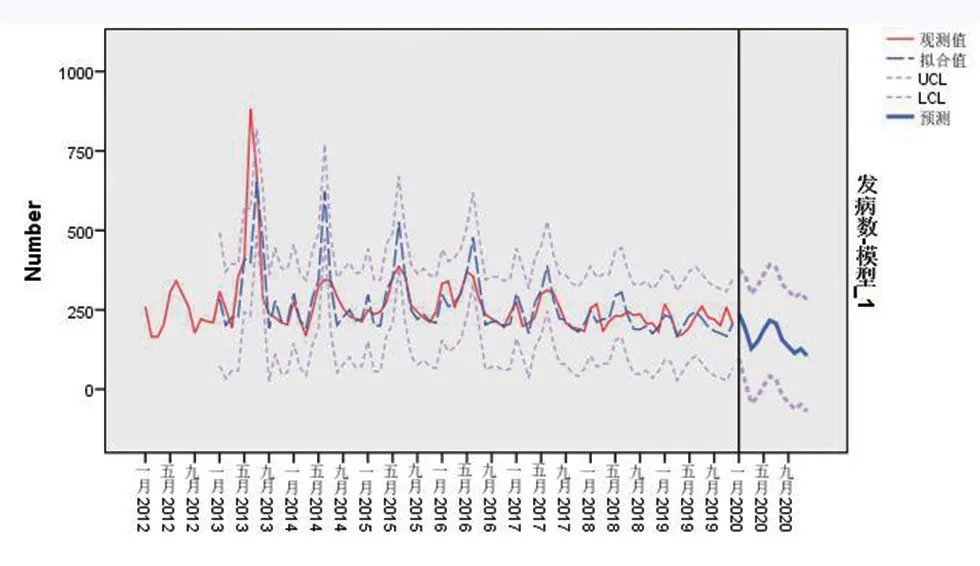
图8 2020年全国每月的疟疾发病数预测图

表4 预测2020年我国疟疾每月发病数与95%置信区间

表5 2014-2020年我国疟疾发病数的预测值与实际值的对比

3 结语

根据2012−2019年的各月疟疾发病数，利用ARI⁃MA复合季节模型，可看出全国疟疾发病数呈明显的以年为周期的震动现象。根据残差分析，自相关和偏自相关系数，正态化的BIC值确定模型的拟合优度，确定了模型ARIMA（1，0，2）（0，1，1）12的适用性，预测了2020年各月度疟疾发病数，均在预测值的95%置信区间内，因此，该模型可以用来预测疟疾的流行发病情况。