基于自调整因子优化的模糊控制器研究

李智敏

（1.闽南理工学院电子与电气工程学院，福建石狮 362700；2.工业自动化控制技术与信息处理福建省高校重点实验室，福建石狮 362700）

近年来，由于模糊控制是一种基于语言的控制器，具有不依赖于被控对象精确的数学模型的优点，而大多数系统和流程非常复杂难以建立精确数学模型，所以模糊控制在各种领域中应用广泛。但是常规的模糊控制规则确定下来在实际的控制过程中无法在线实时修正，若被控系统突发扰动时原控制规则会出现无法满足控制要求，导致系统控制效果变差。因此，为了提高控制精度，改善模糊控制存在的不足，采用优化手段对模糊规则进行改善势在必行。本文在分析集中优化手段后，最后采用自调整因子方法对模糊规则进行改进，最后，对比传统控制，通过MATLAB仿真表明该方案的有效性。

1 优化方法分析及选择

1.1 优化手段分析

遗传算法是一种基于自然选择和基因遗传学原理的优化搜索方法，通过复制、交叉、变异三步基本操作来实现全局寻优，计算简单，功能强大，但是决定寻优方向的目标函数不容易建立[1]。

神经网络优化是利用网络具有的自学习、自适应能力，通过对模糊控制器参数进行神经网络设计，通过训练神经元节点的连接权值，然后实现模糊控制器在线实施调参的目的，但是神经网络算法设计复杂，节点越多，计算量越大[1]。

模拟退火算法可以实现模糊控制器参数的组合优化，但是多个参数需要调整时，目标函数不易寻找[1]。

蚁群算法是根据蚂蚁寻食的生物特性研究出来的一种算法，比较适合不重复路径问题，例如旅行路线，配电电网规划等的优化处理，对模糊控制器优化时达不到较好效果[1]。

粒子群算法是以种群为基础的随机优化方法，是一种全局寻优，但是具有很强的随机性，而且该算法时一种无记忆算法，优化模糊控制器参数时会耗费教长时间[2]。

1.2 优化手段选择

由于在实际应用中针对非线性时变系统模糊控制的控制规则无法在线自行调整导致控制存在不足，因此选择一种优化手段进行解决势在必行，分析几种优化手段的优缺点，本文选择自调整因子作为优化模糊控制器的手段。首先要建立相应的模糊控制器控制系统，然后应用MATLAB仿真软件，在取相同被控对象参数的情况下，对控制系统进行仿真，观察仿真曲线。再应用MATLAB仿真软件对带有自调整因子的模糊控制器进行仿真分析，观察仿真曲线。最后将两种曲线相比较，分析其优越性，实现研究目的。

2 模糊控制器设计及优化

模糊控制是对以往专家工作的总结，根据工艺和现场环境等的条件，利用大量的先验知识，建立模糊的、推理的逻辑的知识库和控制规则[3]。

2.1 模糊控制器的输入输出变量

模糊控制器的输入为偏差和偏差的变化率，E、EC分别为偏差和偏差的变化率为经过模糊化后的对应的模糊变量。模糊控制器的输出模糊变量为U。原理图如图1所示。

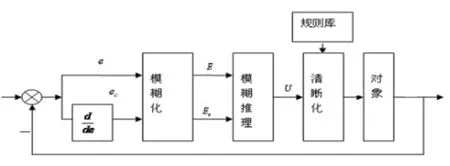
图1 模糊控制系统的基本原理

2.2 输入输出变量的模糊化

输入量和输出量分别有7个，5个和7个模糊子集，既保证了控制精度要求，又不会使计算复杂。

模糊子集的隶属度函数的形状选用三角形波形的隶属度函数对模糊量进行赋值，选用三角形的隶属函数可以减少计算量，使模糊控制简单化。

模糊子集为：

2.3 输入输出量的隶属函数

根据输入量和输出量模糊化的语言值在MAT⁃LAB中建立隶属函数如图2、3、4所示。

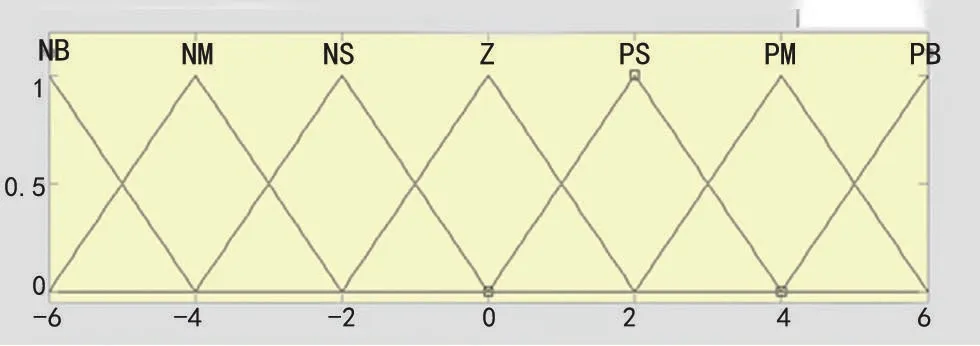
图2 偏差的语言变量范围

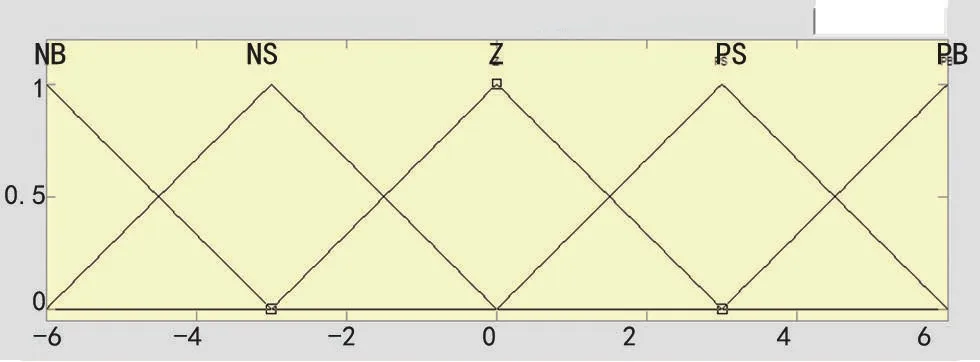
图3 偏差变化率的语言变量范围

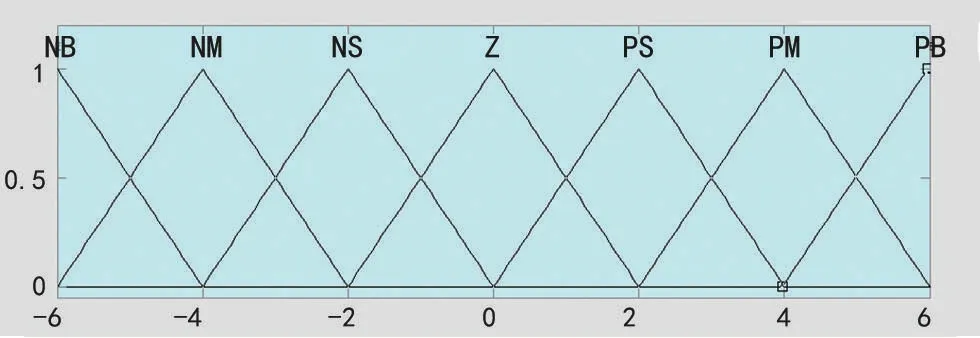
图4 输出量的语言变量范围

2.4 建立模糊控制器的控制规则

模糊推理采用模糊控制规则表，由控制规则可求出模糊关系矩阵R，知道输入、输出的模糊矩阵和模糊关系，可根据矩阵运算和合成运算求出系统模糊输出[4]。

由模糊语句得出的模糊控制规则如下：

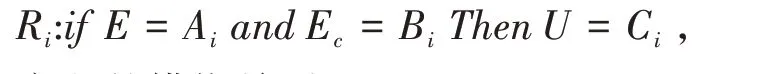
定义的模糊关系：Ri=Ai×Bi×Ci，

模糊推理采用：Ci=(Ai×Bi) ∘Ri。

将模糊量转换为精确量，通过解模糊化完成，一般采用最大隶属度方法，公式如下所示：

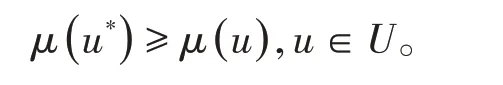
2.5 带有自调整因子模糊控制器设计原则

为了实现自调整控制规则，建立自我调整的因子，通过采用自调整因子来改变控制规则，使用更优的控制规则来进行控制，从而提高模糊控制器的性能，通过对模糊规则的调节[5]。结构使用下列式子表示：

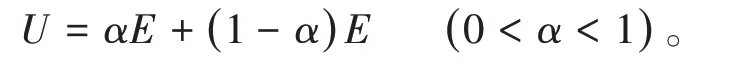
当误差较大时，控制系统的主要任务是消除误差。这时使加权在误差在控制规则中的变化大些。相对的，当误差比较小的时候，系统已经接近稳态，主要控制因素是使系统尽快稳定。因此就需要误差的变化率在控制规则中起重要的作用。根据模糊控制器的原理，加入其输出(自调整因子α)。取α 的论域为{−6，6}，α 的模糊子集为{NB，NM，NS，ZO，PS，PM，PB}[6]。

3 仿真验证及结论

在MATLAB软件命令窗口中输入FUZZY指令，调出模糊控制器，进行语言变量、隶属函数、隶属度、基础论域、语言规则编辑。然后在simulink里面搭建仿真框图，进行仿真验证。如图5所示，被控对象数学模型为：

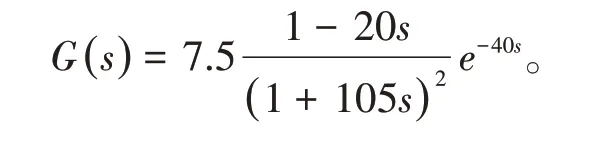
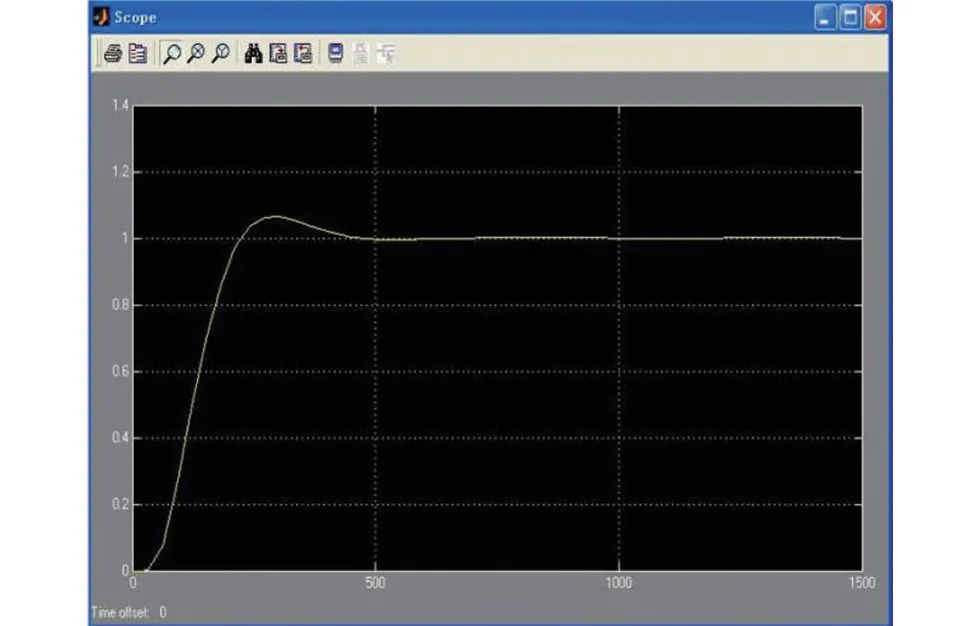
图5 优化控制对比仿真波形

表1 两种手段对比表

通过将具有响应时间相同的基本模糊控制器和带有自调整因子的模糊控制器进行表1的分析对比，表明具有自调整因子的模糊控制器在鲁棒性、超调及稳定时间等几个方面的性能都明显地高于基本模糊控制器。