卫星用复合材料压力容器力学特性研究

于 斌， 张 海， 赵积鹏， 顾森东

(兰州空间技术物理研究所，兰州 730000)

1 引 言

航天器及其分系统需要各种压力容器以贮存液体和气体,如卫星飞船推进系统用气瓶和表面张力推进剂贮箱,空间站推进系统、流体管理系统、环境控制与生命保障系统、科学试验和商业试验系统用各类型压力容器,运载系统的各种气瓶和低温推进剂贮箱等[1]。相对于全金属容器,复合材料压力容器具有质量轻、刚度好、容器特性系数高、可靠性高、抗疲劳性能好、负载工作寿命长、泄漏先于爆破的安全失效模式(LBB)、可设计性强、生产费用低以及研制周期短等诸多特点,其在航天和航空等领域得到越来越广泛的应用[2-5],纤维增强复合材料(CFRP)设计与工艺技术也随之大幅提升[6-9]。

复合材料压力容器(COPV)壳体结构设计解析方法有薄膜理论、基于薄膜理论和网格假设的网格理论以及基于薄膜理论和经典层合板的层合壳理论,由于网格理论简洁准确的特点,目前工程界大都采用网格理论进行COPV结构设计。李卫东等[10]根据网络理论算法,推导了载荷分担型弹性工作内衬COPV计算方程,包括静载各压力下静力学平衡方程和应变连续方程,建立了内衬壁厚的计算公式,但该解法假设内衬在预紧压力和工作压力下分别恰好达到压缩极限和拉伸极限,导致内衬应力计算的准确度有待提高。陈汝训[11]对具有衬里的纤维缠绕COPV结构设计进行了研究,预先确定内衬壁厚,假设容器在最大内压下,内衬和纤维同时达到拉伸极限,推导了应变均衡型/非均衡型缠绕结构的爆破压力计算公式,该解法对薄壁内衬COPV爆破压力的计算较为准确,但不能为内衬壁厚的确定给予指导。目前还未获悉其他涉及金属内衬COPV复合材料网格理论算法推导的研究。

COPV作为航天系统中的关键部件,其研制技术及性能对航天系统有较大的影响,包括(1) COPV结构效率,直接影响航天器有效载荷；(2) COPV可靠性,直接关系整个航天器的成功发射与在轨安全运行；(3) 安全性,发生爆破灾难性失效,对发射塔或航天器产生严重的破坏；(4) COPV应力断裂寿命,直接影响航天器在轨工作寿命；(5) COPV疲劳寿命,影响空间站重复使用COPV的介质充填次数。因此,在COPV结构设计网络理论解析解法方面,迫切需要对该算法进一步优化推导,以满足航天压力容器高结构效率、高可靠性和高安全性的结构设计需求。本文提出了网格理论程序化的优化推导方法,总结了容器壳体力学特性,并介绍了一种高性能航天复合材料气瓶的研制。

2 结构设计

2.1 设计指标与结构分析

COPV技术指标如下,爆破压力≥60 MPa,工作压力≤30 MPa,容积≥100 L,工作寿命15年,疲劳寿命≥50次,性能因子≥30 km。

COPV为单极孔双接头等张力封头圆柱形复合材料气瓶,结构为TC4钛合金超薄壁内衬T1000碳纤维缠绕增强环氧树脂复合材料双层壳体,纤维缠绕线型为环向纤维和螺旋纤维交替缠绕,按照载荷分担型和弹性工作内衬COPV进行设计,根据优化的网格理论算法求解,并通过鉴定试验进行地面试验验证。

COPV在内压载荷作用下,内衬与纤维缠绕复合材料的应力和内压载荷达到静力学平衡,如图1所示,在COPV柱段区域,纵向应力由螺旋纤维在纵向的分量提供,环向应力由环向纤维和螺旋纤维在环向的分量提供,在COPV封头,环向应力和径向应力均由螺旋纤维的相应分量提供。内衬与纤维缠绕壳体应力分布如图2所示,内衬与纤维复合层壳体应力和内压达到静力学平衡,针对超薄壁内衬COPV,复合层是控制应力应变的主体。

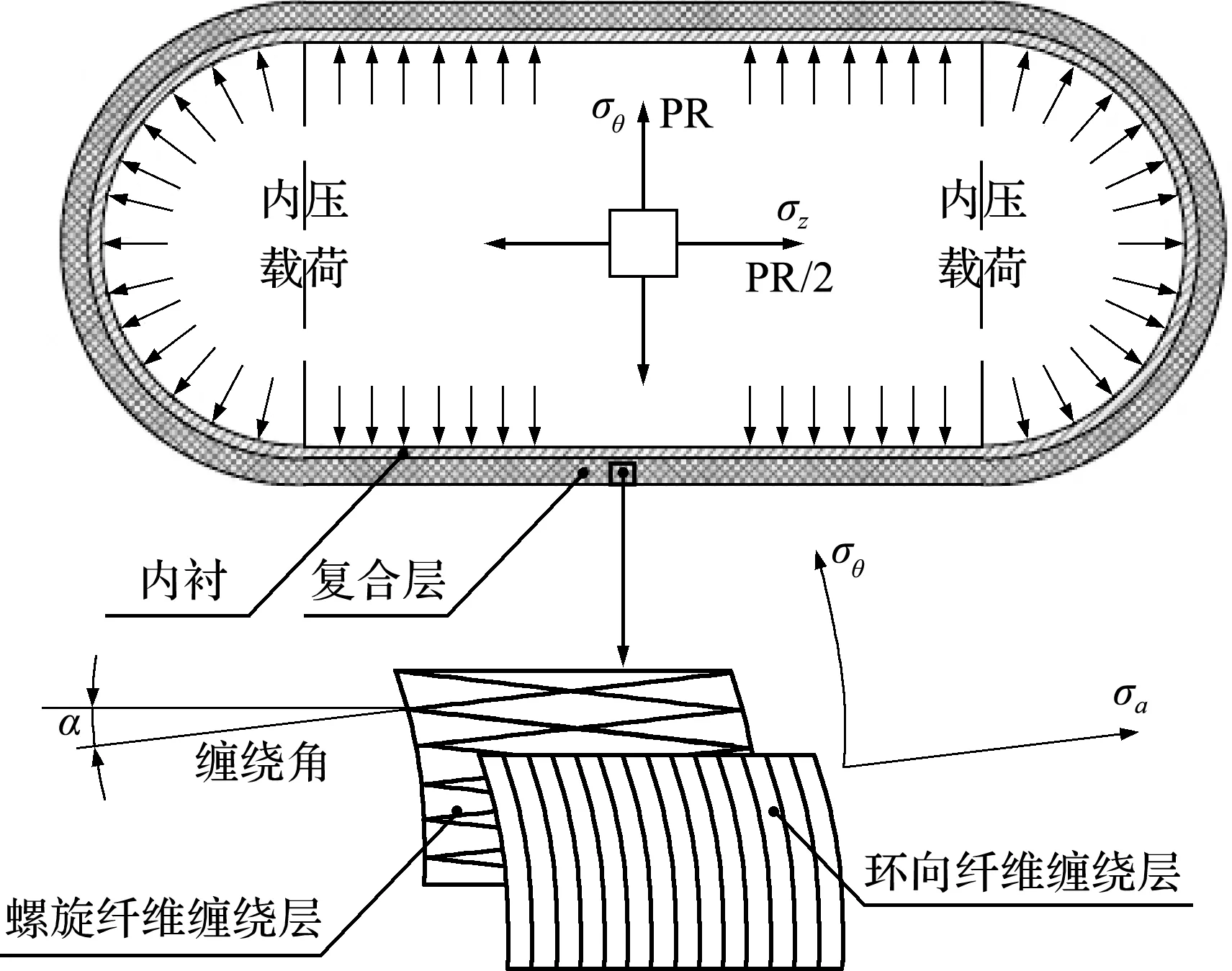
图1 COPV壳体应力分析

图2 内衬与纤维缠绕壳体应力分布

2.2 网格理论优化推导

根据内衬/纤维双层壳体在零压力下壳体预紧应力平衡条件、在内压载荷下的壳体承载静力学平衡条件以及各内压载荷之间的内衬/纤维应力应变协调性原则,建立完整的网格理论方程组。以纤维预紧应力和内衬基础壁厚为自变量,以COPV爆破压力和内衬弹性应力应变范围为边界条件,通过调整纤维预紧应力和选择内衬合理壁厚优化内衬应力应变区间,从而达到网格理论优化设计的目的,COPV网格理论计算参数列入表1。

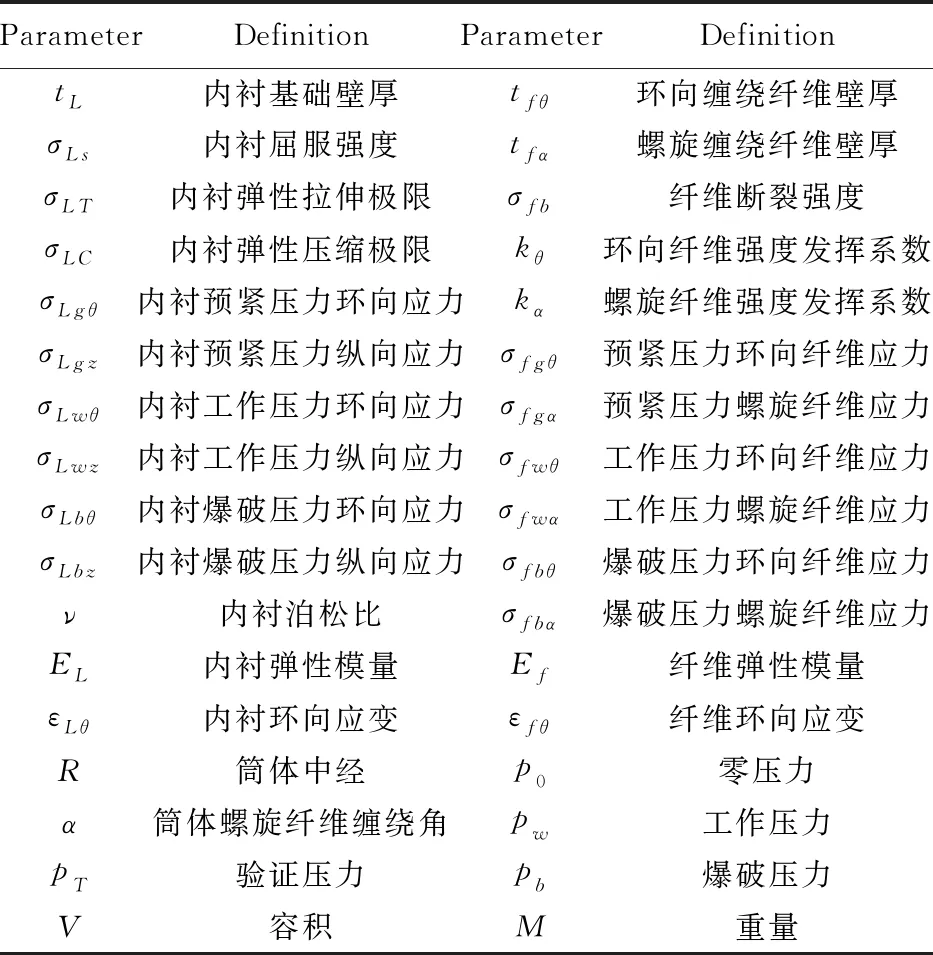
表1 网格理论结构设计参数

2.2.1 零压力下预紧应力静力学平衡方程

在COPV零压力下,通过COPV缠绕张力或自紧压力工艺,使内衬和纤维分别处于压缩应力和拉伸应力状态,从而提高内衬在零压力至工作压力下的弹性应变范围,降低内衬在工作压力下的应力水平,提高COPV的疲劳寿命[12],零压力下内衬/纤维壳体静力学平衡方程可表示为

σf g θkθtf θ+σf g αkαtf α-σL g θtL=0

(1)

σf g αkαtf αcosαcosα-σL g ZtL=0

(2)

2.2.2 工作压力下静力学平衡方程

在COPV工作压力下,按照弹性工作内衬设计条件,内衬由弹性压缩应力应变状态转变为弹性拉伸应力应变,纤维拉伸应力进一步提高,内衬/纤维工作应力与内压载荷产生薄膜应力平衡,工作压力下内衬/纤维壳体静力学平衡方程如式(3,4)所示。上述方程中COPV内衬在零压力和工作压力下的应力并不是预先假设为压缩弹性极限和拉伸弹性极限,而是根据纤维预紧应力和应变协调性原则计算的真实弹性应力,从而区别于以往的网格理论解法,可计算内衬真实等效应变幅和应力水平,为当前结构设计和后续可靠性设计奠定基础[13]。

σf W θkθtf θ+σf W αkαtf αsin2α+σL W θtL=Rpw

(3)

σf W αkαtf αcos2α+σL W ztL=Rpw/2

(4)

2.2.3 爆破工作压力下静力学平衡方程

在COPV爆破压力下,内衬由拉伸弹性应变过渡到拉伸塑性应变,纤维拉伸基本达到抗拉强度,内衬材料屈服后是应变强化塑性变形,可将内衬弹塑性应力应变简化为双线性等向强化模型,计算内衬塑性应力。本文方程将内衬应力简化为弹性极限,这样既可保证纤维复合层具有足够的强度裕度,又可保证该算法在COPV初步设计中简洁高效[14]。在塑性内衬网格理论的推导中,零压力下内衬处于弹性压缩应力状态,工作压力和爆破压力下内衬均处于塑性应力应变状态,内衬增压过程中,经历弹性压缩回弹、弹性拉伸变形和塑性拉伸变形,因此将内衬上述三个应变方程累加近似等于纤维弹性拉伸应力应变方程,建立双层壳体的应变位移连续方程,即可对塑性内衬网格进行理论推导。爆破压力下静力学平衡方程可表示为

σf b θkθtf θ+σf b αkαtf αsin2α+σL b θtL=Rpb

(5)

σf b αkαtf αcos2α+σL b ztL=Rpb/2

(6)

2.2.4 应变协调方程

COPV在零压力至工作压力过程中,根据应力应变连续条件,内衬/纤维在内压作用下的应力应变协调一致,并无相对滑移或分层等缺陷,内衬和纤维的环向应变相同[15],建立零压力至工作压力下的内衬/纤维应变协调方程可表示为

εL θ=εf θ

(7)

εL 1 θ=(2-υ)|σL W θ-σL g θ|/2EL e

(8)

εf θ=(σf W θ-σf g θ)/Ef

(9)

2.3 联立求解与应力分析

根据载荷分担型弹性内衬COPV网格理论方程联立求解,分别针对0.6 mm，0.8 mm，1.0 mm，1.2 mm，1.4 mm，1.6 mm，1.8 mm，2.0 mm和 2.2 mm 基础壁厚内衬COPV应力特性进行研究。弹性内衬COPV网格理论采用9个方程组联立求解,以纤维预紧应力为自变量,以COPV爆破压力为内衬与纤维复合层厚度计算的边界条件,通过内衬壁厚变化推导复合层厚度,根据内衬弹性应力应变工作条件优化纤维预紧应力,根据COPV性能因子和内衬刚度等参数确定内衬最佳壁厚,根据上述算法编制计算软件程序,通过计算软件程序完成COPV网格理论的优化计算。通过零压力下COPV轴向和环向静力平衡方程(1，2)求解,得到零压力下内衬压缩应力随纤维预紧应力的变化曲线,如图3所示。可以看出，内衬压缩应力随纤维预紧应力增加而线性增加；内衬壁厚增加,内衬压缩应力对纤维预紧应力敏感度减低,内衬压缩弹性范围对应的纤维预紧应力区间扩大；内衬壁厚降低,内衬对纤维预紧应力的控制精度要求提高,纤维许用预紧应力区间减小,内衬相应所需达到屈服强度的纤维预紧应力值降低。

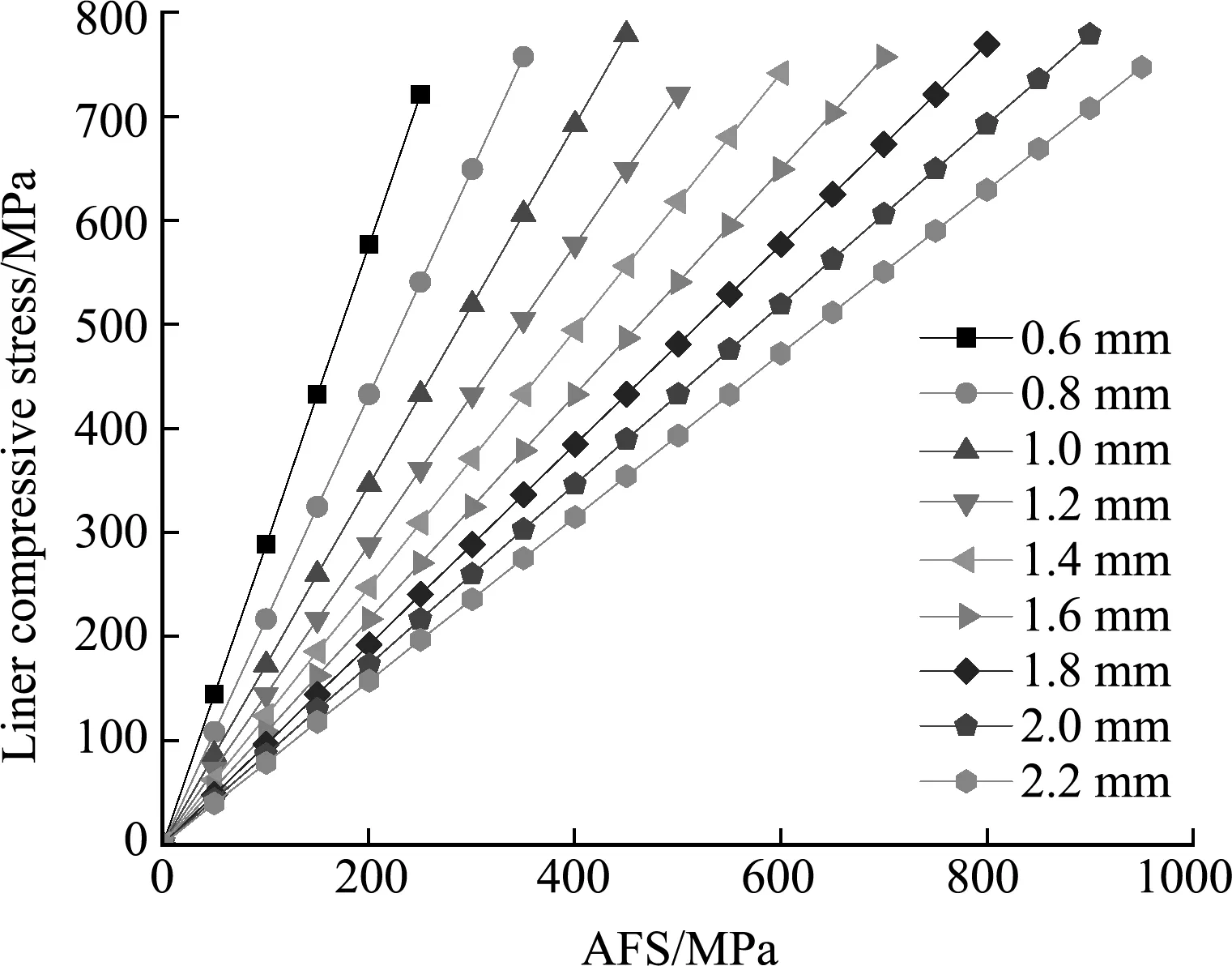
图3 内衬压缩应力与纤维预紧应力曲线

将COPV 零压力下静力学平衡方程(1，2)、工作压力下静力学平衡方程(3，4)、爆破压力下静力学平衡方程(5,6)以及零压力至工作压力应变协调方程(7～9)综合联立求解,得到工作压力下纤维工作应力随纤维预紧应力变化曲线,如图4所示。可以看出，纤维工作应力随纤维预紧应力增加而增加；内衬壁厚增加,内衬分担载荷比例增加,纤维工作应力降低,内衬弹性范围对应纤维应力区间增加,曲线斜率先高后低,这是由于纤维预紧应力已使内衬屈服发生弹塑性应力应变。

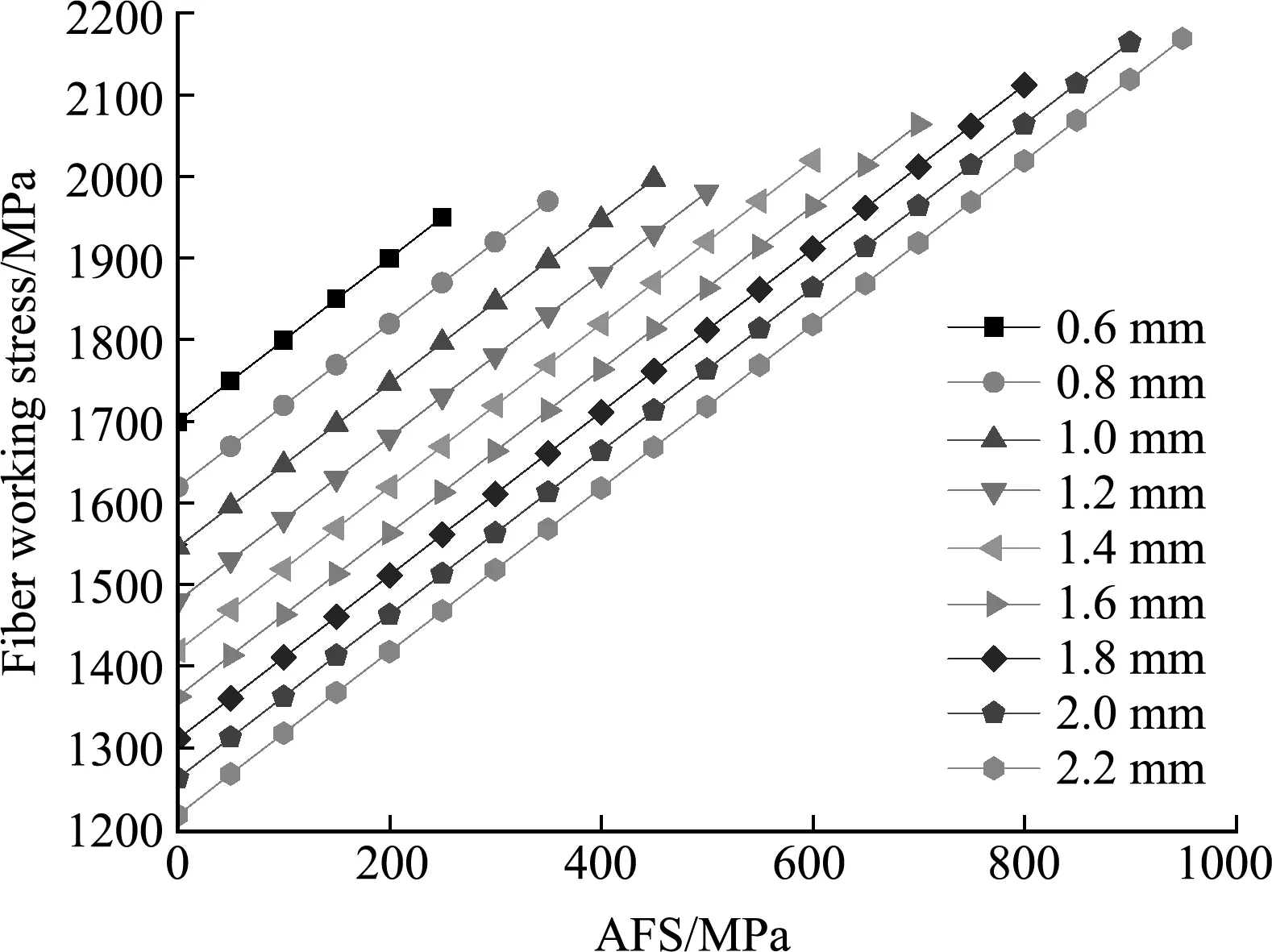
图4 纤维工作应力与纤维预紧应力曲线

内衬工作应力与纤维预紧应力的关系如图5所示。可见，随着纤维预紧应力提高,内衬工作应力降低。COPV在零压力至工作压力下的内衬/纤维双层壳体协同应力应变过程中,纤维弹性拉伸应变区间近似相等,纤维预紧应力提高,零压力下内衬压缩应力提高,内衬压缩应变区间增加,纤维拉伸弹性应变区间等于内衬压缩应变与内衬拉伸应变之和,见方程(7～9),内衬拉伸应变减少,COPV工作压力下内衬拉伸应力降低。内衬壁厚增加,内衬工作应力受纤维预紧应力影响的敏感度降低,COPV结构设计时，在内压指标、复合层壁厚和纤维预紧应力确定的情况下,内衬壁厚和内衬工作应力近似呈反比,内衬壁厚增加,工作压力下内衬应力降低。

内衬承担载荷比例与纤维预紧应力关系如 图6 所示,内衬承担载荷比例随内衬壁厚的增加而增加,随纤维预紧应力的增加而减少。内衬壁厚增加,由于薄膜应力影响,在相同应力应变的情况下,内衬承压能力提高,内衬分担载荷比例增加；纤维预紧应力提高,纤维工作应力提高,内衬工作应力降低,分担载荷比例降低。

从弹性内衬网格理论计算结果考虑,内衬壁厚为0.6 mm～2.2 mm均满足弹性内衬COPV设计,内衬壁厚越厚,内衬加工与纤维缠绕工艺越好。从航天COPV轻质高强特点考虑,COPV性能因子(Pb×V/M)需大于30 km,COPV性能因子随内衬壁厚增加而降低,递减的幅度随内衬壁厚增加而减弱,如图7所示,因此内衬壁厚≤1 mm。内衬外压稳定性随壁厚增加而增加,随筒体直径增大而降低,因此该型COPV内衬壁厚≥0.7 mm。综合

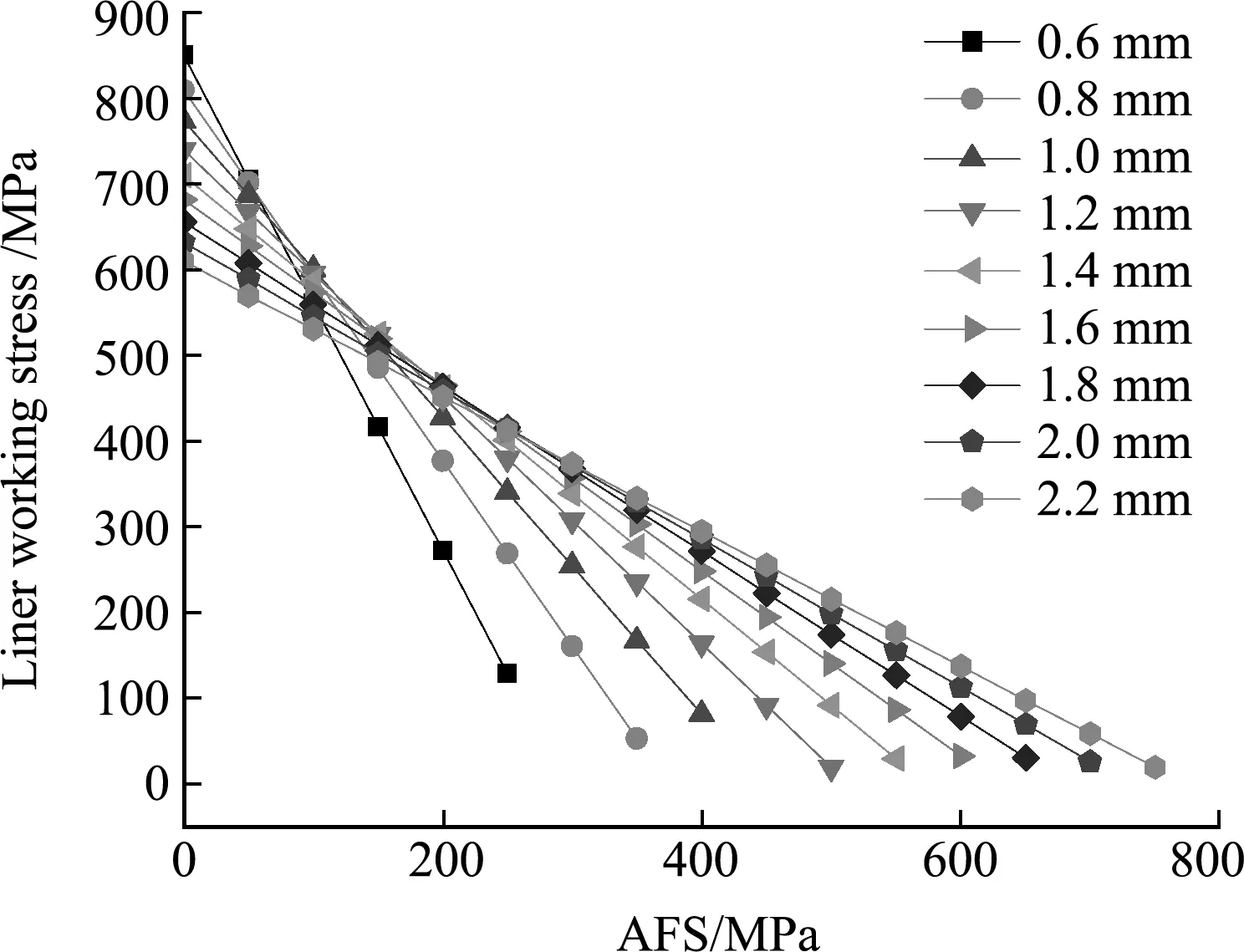
图5 内衬工作应力与纤维预紧应力曲线

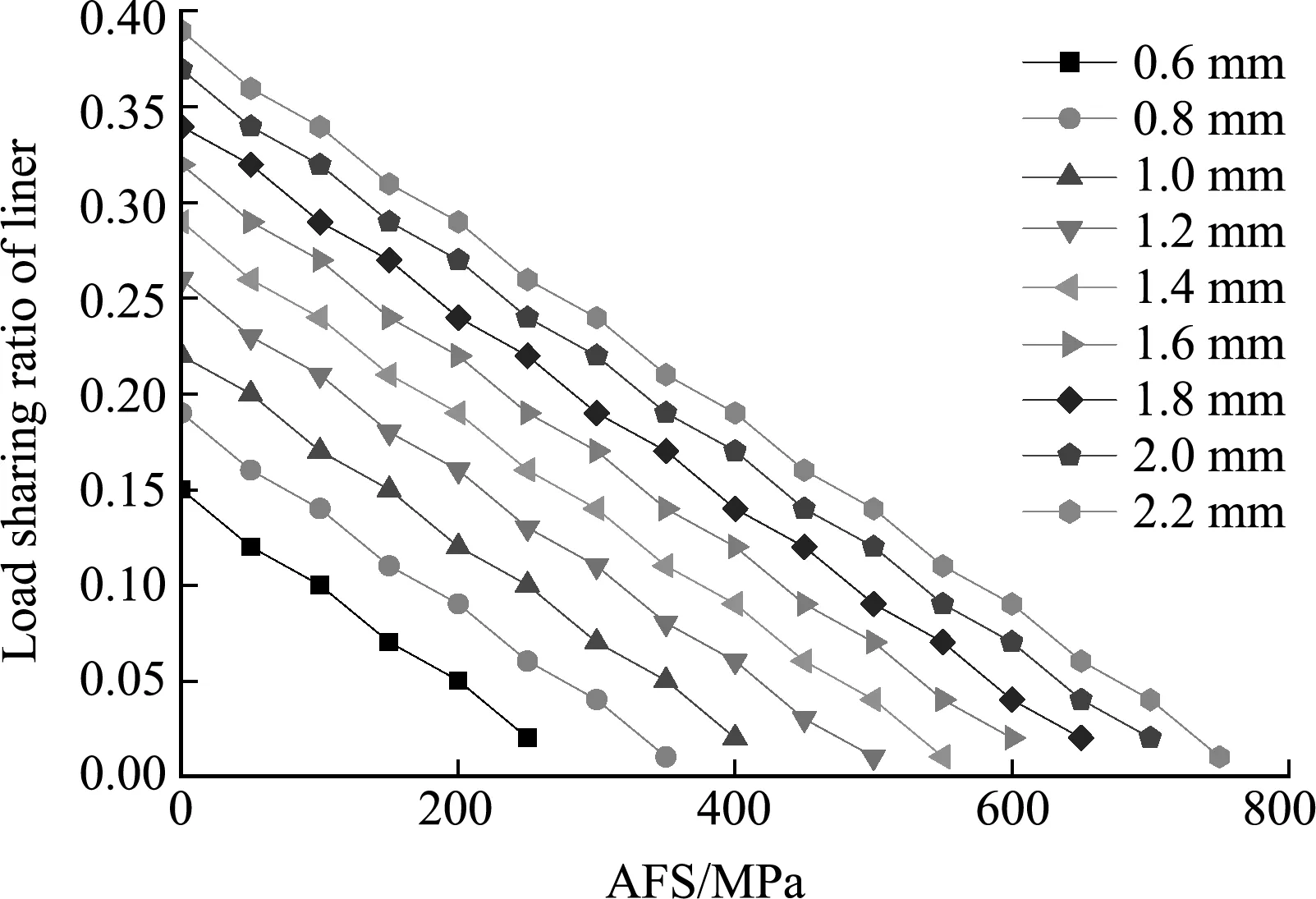
图6 内衬载荷分担比例与纤维预紧应力曲线

COPV性能因子、内衬外压稳定性与刚度、内衬精密加工、焊接成型和加工公差等因素,确定内衬基础壁厚为0.8 mm,可提高结构效率,并发挥轻质高强特性。

以内衬壁厚0.8 mm开展COPV纤维预紧应力优化设计,在纤维不同预紧处理后内衬应力与内压关系如图8所示,纤维预紧应力增加,内衬压缩应力增加,纤维预紧应力从0 MPa～350 MPa过程的8个应力区间变化过程中,COPV内衬在零压力下和工作压力下的应力(σ0,σPW)依次为(0 MPa,780 MPa),(-108 MPa,702 MPa),(-216 MPa,594 MPa),(-324 MPa,486 MPa),(-432 MPa,377 MPa),(-541 MPa,269 MPa),(-649 MPa,161 MPa)和(-757 MPa,53 MPa),COPV内衬在零压力下和工作压力下的应力与屈服强度比(σ0/σS,σPW/σS)依次为(0%,100%),(-14%,90%),(-28%,76%),(-42%,62%),(-55%,48%),(-69%,35%),(-83%,21%)和(-97%,7%),纤维预紧应力越大,内衬工作应力越大,接近60 MPa爆破压力时,内衬进入塑性应力应变状态。

不同内压下，内衬应力与纤维预紧应力关系如图9所示。美国运输部(DOT)于2000年11月颁发的DOT CFFC-2000《全缠绕碳纤维增强铝内胆气瓶的基本要求》对金属内衬复合材料压力容器壳体应力预紧处理进行了规定,包括(1)预紧压力卸载后,零压力下内衬压应力要大于材料屈服极限的60%,且不得超过材料屈服极限的95%;(2)工作压力下内衬拉应力不得超过材料弹性极限的60%。当纤维预紧应力为250 MPa时,零压力下内衬压缩应力为541 MPa,应力与屈服强度比为69%,工作压力下内衬拉伸应力为269 MPa,应力与屈服强度比为35%,满足DOT CFFC-2000标准要求。COPV在工作压力至验证压力范围内,内衬始终处于弹性应力应变状态,满足COPV在轨服役的可靠性设计。

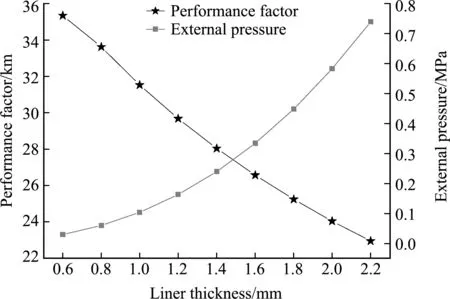
图7 性能因子和外压性能与内衬壁厚曲线

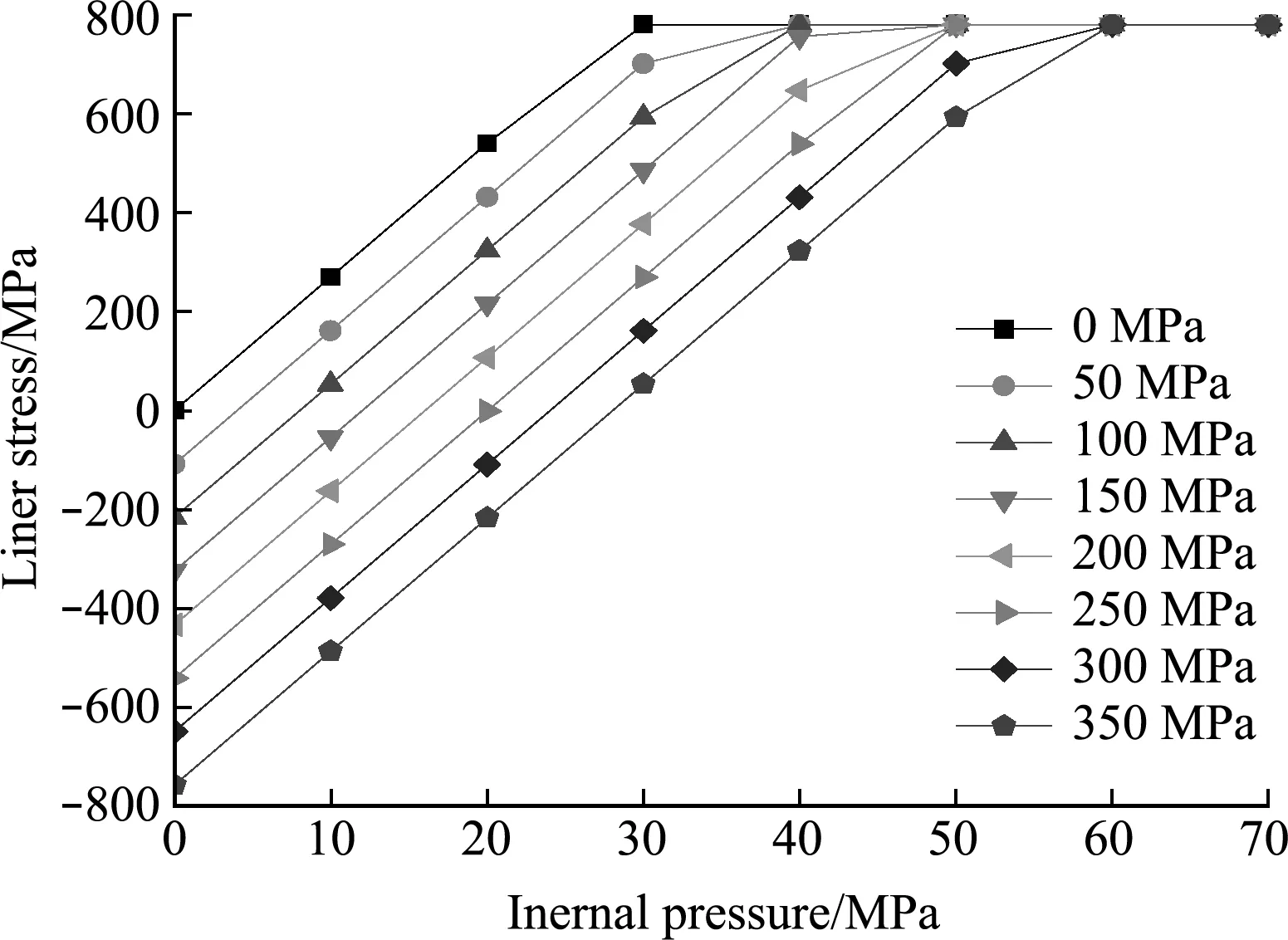
图8 不同预紧处理的内衬应力与内压关系

不同内压下，纤维应力与纤维预紧应力关系如图10所示,纤维预紧应力提高,工作压力下纤维应力提高,由于内衬分担载荷比例较小,零压力至工作压力下的纤维弹性应变区间近似相等,预紧应力技术充分发挥了碳纤维高强度的特性。

有无应力优化处理的内衬应力对比如图11所示,无预紧处理时,工作压力下内衬进入塑性应力应变状态,不满足弹性内衬设计和高周疲劳寿命要求,在轨服役的可靠性大大降低,内衬应力状态也不符合DOT CFFC-2000标准要求。预紧应力技术处理后,零压力下,内衬处于弹性压缩应力应变状态,压缩应力为541 MPa,在后续升压的过程中,内衬弹性压缩应力应变减少,升压至20 MPa时,内衬压缩应力应变恢复至0,继续升压,内衬进入弹性拉伸应力应变状态,在30 MPa时,内衬弹性拉伸应力为269 MPa,在后续升压过程中,当接近50 MPa时,内衬进入塑性应力应变状态,预紧应力技术扩大了内衬弹性应力应变区间。

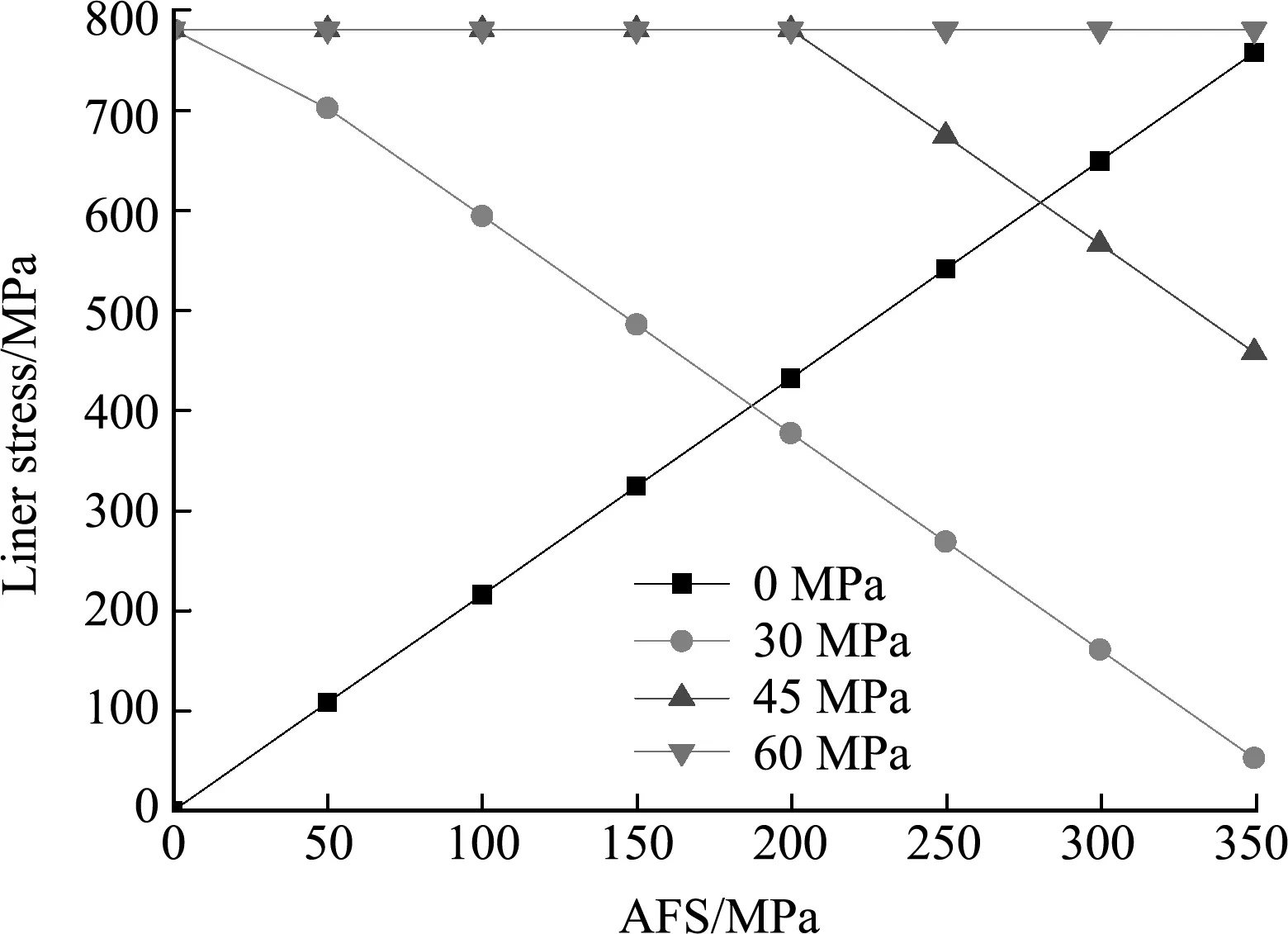
图9 不同内压下内衬应力与纤维预紧应力关系

图10 不同内压下纤维应力与纤维预紧应力关系

3 鉴定试验

根据优化后的网格理论算法完成了结构设计,采用TC4钛合金超薄壁内衬和T1000碳纤维缠绕增强环氧树脂复合材料完成了COPV的制造,顺利通过全部鉴定试验,鉴定试验结果列入表2,COPV爆破压力为69.5 MPa,满足设计要求。

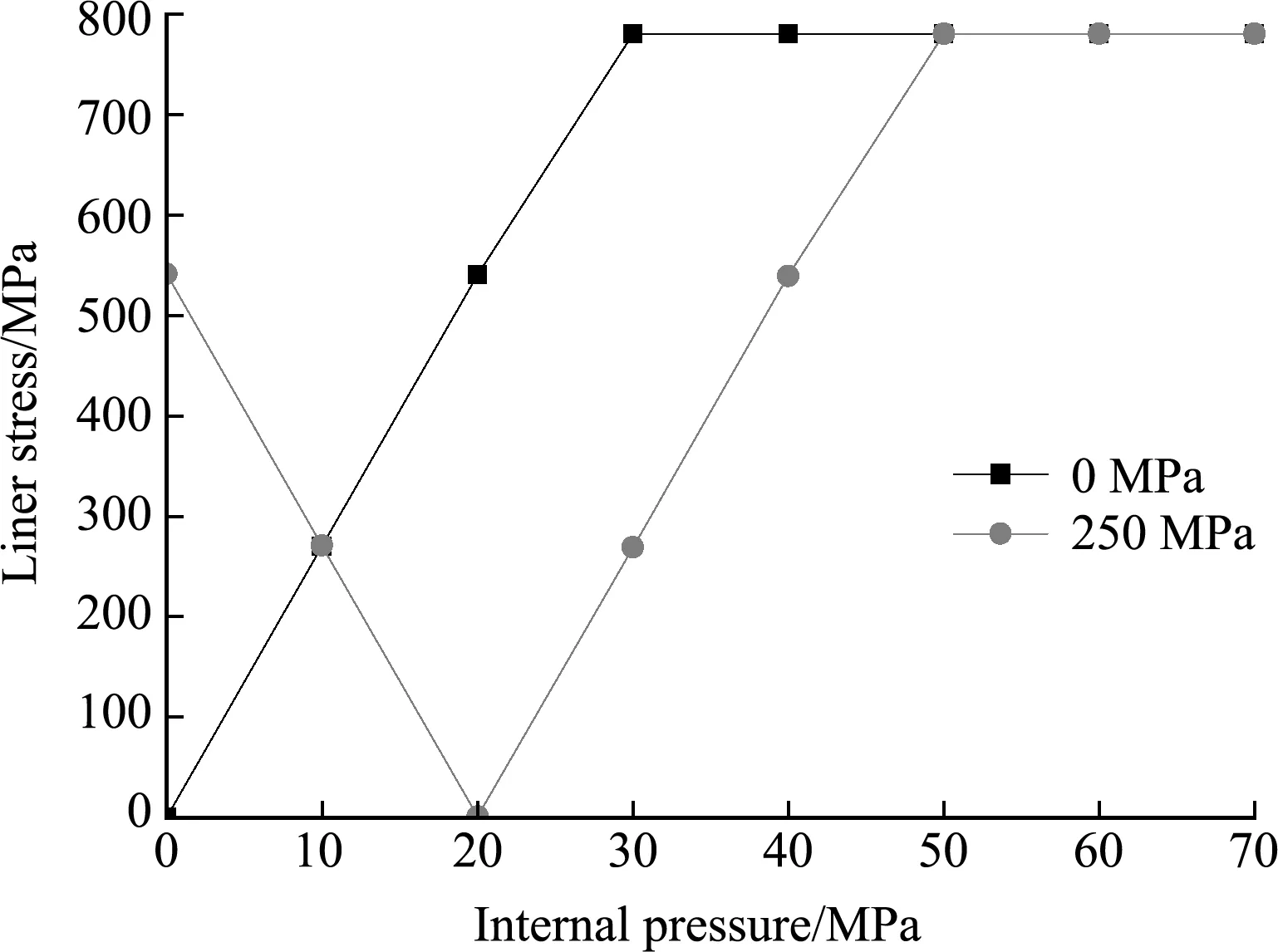
图11 有无应力优化处理的内衬应力对比

4 结 论

复合材料结构属于无限静不定问题,网格理论是将静不定问题简化成静定问题,由平衡方程进行应力求解,国内外通过工程实践,证实网格理论可以为纤维增强树脂单纯的复合材料缠绕壳体进行准确的强度计算。金属内衬COPV广泛应用于航天等军工领域,属于双层壳体耦合的结构应力计算,内衬/纤维需按载荷分担型结构设计,通过方程迭代推导研究表明,采用传统的网格理论计算金属内衬COPV双层壳体结构强度时,存在内衬应力计算精度差、复合材料结构强度安全裕度和内衬疲劳寿命不能确保满足的问题。

本文根据静力学平衡条件和应力应变协调性原则,建立了内衬/纤维双层壳体在零压力、工作压力及爆破压力下的静力学平衡方程和各内压载荷之间的应变连续方程,优化传统网格理论算法,以纤维预紧应力为自变量,联立方程组进行矩阵式求解,能够准确得到不同内衬壁厚下的双层壳体在各内压阶段的应力值,为内衬壁厚计算、纤维预紧应力区间确定和复合材料结构强度等计算提供了依据,满足金属内衬COPV综合优化设计要求,所研制COPV通过全部鉴定试验,性能因子达到35 km,在性能方面与国际先进水平接轨。

优化后的网格理论解法提高了计算精度,适用于弹性内衬COPV强度设计,可为同类产品初步设计、强度计算和相似结构优化设计提供理论指导和计算参考,结合内衬的材料、结构以及工艺等特性,可确定金属内衬的最佳基础壁厚,也有助于提高航天COPV可靠性和安全性的设计水平。