基于坐标变换精确计算近奇异积分的双向sinh变换法

谢贵重， 董云桥， 钟玉东， 周枫林

(1.湖南大学 机械与运载工程学院，长沙 410082；2.郑州轻工业大学 机电工程学院 河南省机械装备智能制造重点实验室，郑州 450002；3.南华大学 机械工程学院，衡阳 421001)

1 引 言

在典型的积分类型数值方法,如边界元法和扩展有限元法中[1-6]，由于采用奇异基本解或者奇异形函数，导致被积函数具有近奇异性。如果不能精确有效地计算这类积分，该类方法的计算精度会受影响甚至会造成错误的结果。

围绕近奇异积分的精确计算产生了许多方法，如解析和半解析方法[7,8]、自适应细分方法[9-11]及非线性变换方法(包括sinh变换和距离变换)[12-17]。解析与半解析方法具有很高精度，然而需要复杂的数学公式推导，限制了该方法的应用范围。自适应细分方法是一种稳定且通用的方法，但是需要引入额外的积分点，计算量巨大，这种方法在计算超薄型结构时会严重降低计算效率。非线性变换也是应用较广的一种方法，在非线性变换中，sinh变换是一种比较有数学含义的方法，可以用迭代将积分点集中在近奇异点附近，以达到改善积分精度的目的。

在传统的sinh变换方法中，首先需要对其进行极坐标变换和坐标变换。文献[18]指出，在最近点靠近角点或者积分边界的时候，被积函数在经过极坐标变换后的环向或经过坐标变换后的两个方向仍然具有很明显的近奇异性，需要特别关注。sinh变换结合环向变换是一种有效的方法，但是积分单元需要划分多个三角形，并且在环向需要2倍的高斯积分点，导致计算效率受到影响。因此，本文采用一种可以将近奇异性在两个方向进行分离的(α,β)坐标变换法[3]，再根据复变函数极点理论，让两个方向的sinh变换分别在极点处实施。最后，给出几个不同类型单元上近奇异积分的数值算例，结果对比表明，双向sinh变换结合坐标变换可以明显提高近奇异积分的计算精度，并且具有较好的稳定性，同时让近奇异积分对最近点的敏感性降低。

2 近奇异积分形式及积分子单元划分

2.1 近奇异积分形式

在三维边界元法中，边界积分形式为

(λ>0)(1)

式中f(F,S)为标量函数，其数值积分可以通过标准的高斯积分求得。F为场点，设其坐标为(x,y,z)。S为源点，设其坐标为(x0,y0,z0)。λ取值为0.5或1。为了简单起见，考虑积分区域为一个落在XY平面上的三角形，设源点到该三角形的最近点为(x0,y0,0)。将源点到最近点的距离定义为r0。则式(1)可以变形为

(2)

式中由于代入了场点和源点坐标，f(F,S)的形式变换为f1(x-x0,y-y0,z0)。

(3)

式中θ1,θ2和R(θ)可以从文献[18]找到。

为与文献[18]的方法进行对比，本文考虑如式(4)类型的积分，

(4)

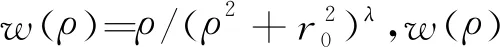
2.2 与近奇异积分结合的单元划分

在近奇异积分单元的划分中，首先找到源点到积分单元的最近点。如果最近点落在单元内部，将四边形单元划分为四个积分子单元如图1(a)所示；如果最近点落在四边形单元边上，将四边形单元划分为三个积分子单元如图1(b)所示，故最多分出四个三角形子单元。

3 结合(α,β)坐标变换的双向sinh变换法

3.1 (α,β)坐标变换法

从图2可以看出，一个三角形积分子单元通过(α,β)坐标变换对应成了一个标准的四边形，具体变换如下，

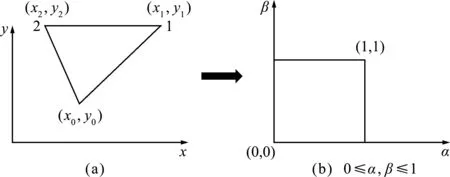
图2 (α,β)坐标变换系统

(5)

将式(5)代入式(2)得

(6)

式中J=αSΔ为(α,β)坐标变换的雅克比。SΔ为三角形子单元面积的2倍,g(β)=[(x1-x0)+(x2-x1)β]2+[(y1-y0)+(y2-y1)β]2，为了方便，记g(β)=aβ2+bβ+c。式(6)可以进行如下分离，

(7)

3.2 双向sinh变换及迭代sinh变换法

由式(7)可知，α和β方向的近奇异性都应考虑，即需要考虑如下两种类型的近奇异积分，

(8)

(9)

针对式(8)近奇异积分的处理，可以使用如下sinh变换,

(10)

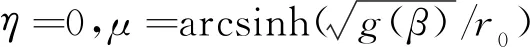
根据g(β)的表达式，式(9)可以写为

(11)

(12)

式中β∈[0,1]⟺e∈[0,1]

使用此sinh变换的雅可比为

最终得到对式(7)变换之后的积分形式为

(13)

然后对式(13)分别在ξ和e两个方向采用高斯积分，即可得到最终的数值积分结果。

4 数值算例

将与基于极坐标的sinh变换及其与环向变换相结合的结果进行对比，来验证本文方法的精确性和有效性，相对误差定义为

(14)

式中Inum为使用变换的数值积分方法，Iexa为参考解，可以通过单元细分并使用大量高斯积分点的方法来获得。接近率定义为

(15)

式中r0为最近距离，Saera为积分单元的面积。

在以下算例中，用符号rsinh表示极坐标下单向sinh变换，rsinh2表示极坐标下单向迭代sinh变换，αsinhβsinh表示(α,β)变换与双向sinh变换的结合(即本文方法)，每一块积分子单元均使用16×16的高斯积分。

4.1 针对线性四边形单元的近奇异积分

考虑XY空间内一个标准的四边形线性等参元，四个顶点分别为(-1.0,-1.0)，(1.0,-1.0)，(1.0,1.0)和(-1.0,1.0)。最近点在四边形内的参数坐标分别为(0.9,0.9)，(0.5,0.5)，(0.9,0.0)和(0.98,0.98)，本算例f1=1，计算结果列入表1和表2。

由表1和表2可知，针对平面单元的近奇异积分，αsinhβsinh 方法要优于其他几种方法，尤其是最近点靠近边界的情况。

4.2 针对二次四边形单元的近奇异积分

考虑XYZ空间内一个二次的四边形等参元，其八个顶点分别为(1.0,1.0,0.1)，(-1.0,1.0,0.1),(-1.0,-1.0,0.1)，(1.0,-1.0,0.1)，(0.0,1.0,0.1)，(-1.0,0.0,0.1)，(0.0,-1.0,0.2)，(1.0,0.0,0.2)，(0.0,0.0,0.2)。最近点在四边形内的参数坐标分别为(0.9,0.9)，(0.5,0.5)，(0.9,0.0)和(0.98,0.98)。本算例f1=1，数值计算结果列入表3和表4。

由表3和表4可知，针对二次单元的近奇异积分，相比其他方法，αsinhβsinh方法都可以获得较好的计算结果，尤其是最近点靠近边界时。

表1 λ =0.5，最近点不同时平面单元的计算误差

表2 λ=1.0，最近点不同时平面单元的计算误差

表3 λ=0.5，最近点不同时二次单元的计算误差

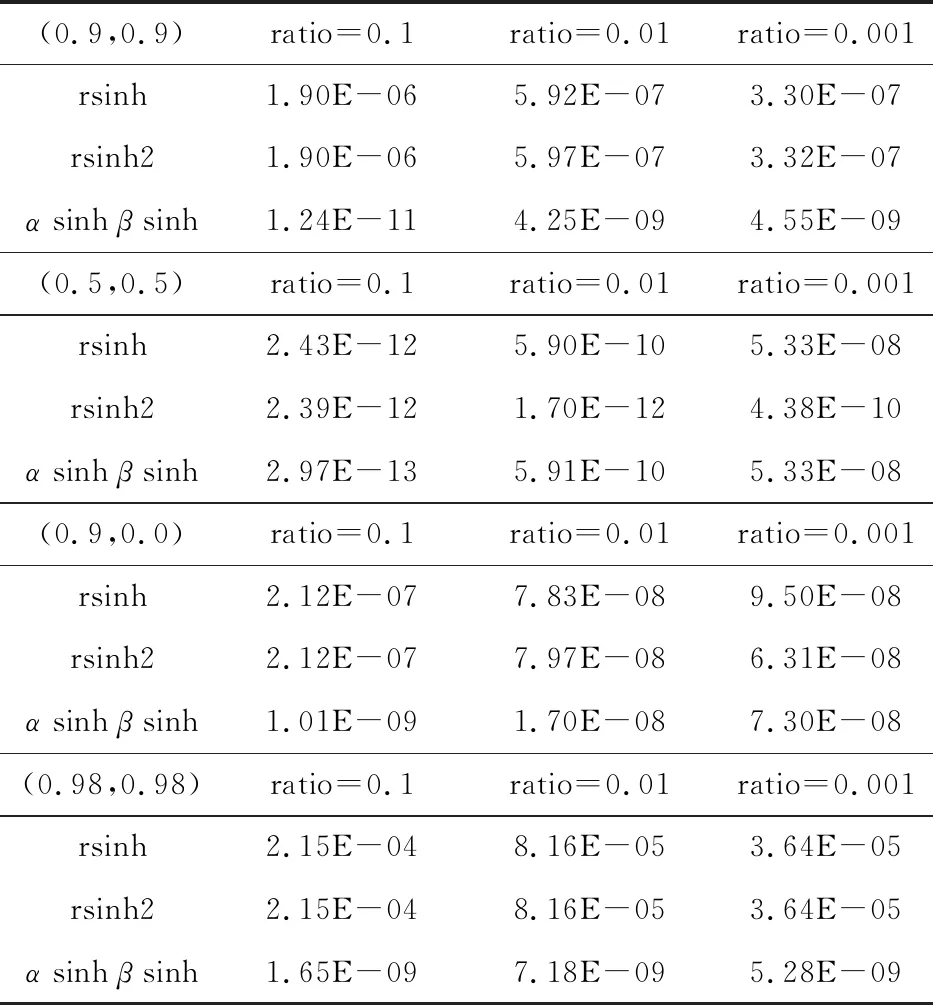
表4 λ=1.0，最近点不同时二次单元的计算误差

5 结 论

本文提出了一种双向sinh变换法来计算四边形单元的近奇异积分。双向sinh变换方法主要结合(α,β)坐标变换和sinh变换。首先,利用(α,β)坐标变换来分离α方向与β方向的近奇异性;再基于α方向与β方向的近奇异积分形式，构造了sinh变换和迭代sinh变换来消除其近奇异性;最后,通过数值算例验证了本文方法的精确性。数值结果表明，对于最近点靠近单元边界时引起的积分子单元顶端大张角和边长比较大的情况，双向sinh变换能保持相当高的计算精度和稳定性，是一种理想的消除近奇异性的方法。