温度循环载荷对柔性接头界面损伤的影响

王 才， 史宏斌， 刘 沛， 屈转利， 刘统斌， 刘 芹

(西安航天动力技术研究所，燃烧、热结构和内流场重点实验室，西安 710025)

1 引 言

柔性接头由金属前法兰、后法兰、金属或非金属增强件与橡胶弹性件交替粘接而成，可以作全轴摆动，并且摆动重复性好，是固体火箭发动机推力矢量控制的核心部件[1,2]。柔性接头的结构决定其包含了大量的粘接界面，而固体火箭发动机工作过程中需保证密封性，因此柔性接头界面的质量直接决定了发动机的工作性能[3]。固体火箭发动机在生产、运输和储存的过程中都会受到环境湿热和老化载荷的作用，不同时刻不同地点所处环境的湿度和温度均不相同。固体火箭发动机在生产、运输和储存的过程中，粘接界面的力学性能存在一个退化过程，致使柔性接头在较低的载荷工况下就会发生界面损伤，带来柔性接头密封失效问题。

对于柔性接头这样特殊功能的胶接件，常见的失效模式为粘接界面的脱粘。内聚力模型是研究粘接界面的主要理论之一，最早由Dugdale等[4,5]提出，由Needleman等[6-9]逐步完善，当前已在界面损伤分析中广泛应用。赵宁等[10]采用内聚力模型仿真铝板环氧树脂胶接接头，模拟了胶层加载过程中的裂纹扩展过程，计算结果同试验值吻合较好。杨小辉等[11]采用零厚度的内聚力模型单元模拟了胶接接头的分层损伤过程，仿真结果与试验结果一致。贾登等[12]通过双悬臂夹层梁试验研究了三元乙丙橡胶薄膜粘接界面I型裂纹的温度相关性，采用线弹性断裂力学方法获取了粘接界面的断裂能，并利用内聚力模型模拟了双悬臂夹层梁试验，结果表明，采用未经修正的线弹性断裂力学理论获得的断裂能模拟的结果存在较大误差，而采用修正后的参数得到的仿真结果与试验结果相符。韩啸等[13]通过试验研究了韧脆性质不同的两种胶粘剂的剪切强度在循环温度场中的退化，结果表明，温度循环可使两种胶粘剂出现不同程度的退化，且退化趋势随时间的推移逐渐趋于稳定，最后采用内聚力模型分析了胶层的破坏过程，结果表明胶层在经历温度循环载荷作用后，剥离应力与剪切应力在胶接区边缘处有明显集中。施志伟[14]开展了胶接接头在循环温度载荷下的老化试验，同样表明了温度循环会促进胶层的老化，同时，引入衡量胶层老化的环境退化参数，建立了胶层的环境退化模型，通过内聚力模型准确预测了老化试件的剩余强度。Walader等[15]在玻璃转化区域内研究了温度对一种环氧胶粘剂内聚力参数的影响。在 -30 ℃～80 ℃准静态加载下分别测得了I型与II型裂纹的初始刚度、断裂强度及断裂能，并采用双线性内聚力模型模拟了胶层的损伤情况。结果表明，除了I型裂纹的断裂能外，其他所有的内聚力参数值均随着温度的升高而下降，该温度范围内I型裂纹的断裂能表现出温度无关性，而II型裂纹的断裂能从-30 ℃至80 ℃时下降了2/3，且试验结果与仿真结果符合较好。文献[16,17]考虑了双悬臂夹层梁试验过程中试样件变形的大位移、加载块及裂纹尖端旋转等因素对I型裂纹断裂能的影响，并提出了修正公式，结果表明，采用修正后的断裂能的仿真结果与试验结果符合较好。Loh等[18]通过缺口弯曲试验和混合模式失效试验研究了湿热环境下界面的失效情况，试验测得了界面间的强度参数，并采用内聚力模型模拟了缺口弯曲试验和混合模式失效试验，通过试验与仿真相结合，确定了不同湿热环境下界面的断裂能，研究结果显示，不同湿热环境下界面的断裂能有明显的退化，且断裂能大小与试验方法无关。Liljedahl等[19]研究了湿环境下铝板与复合材料异种基板胶接接头的耐久性能，在不同湿度下进行了测量内聚力参数的力学试验，并采用内聚力模型成功预测了铝板单搭接接头的剩余强度退化规律。

通常对柔性接头进行有限元分析时，把重点都放在了弹性件的分析上，在增强件与弹性件间采用捆绑约束，忽略了界面的力学性能[20-22]，文献[23]通过分析粘接面的轴向应力与剪应力，得到轴向应力偏大是粘接面破坏的主要原因，但未提出粘接面的本构模型；文献[24]通过分析弹性件表面的法向与切向应力来计算弹性件的安全系数以反映柔性接头的密封可靠性，但未给出粘接界面损伤本构模型，且上述分析仅能对柔性接头摆动时的设计裕度进行评估，不能对柔性接头的损伤进行精确评估。当前，研究温度对柔性接头的影响主要是在短期下温度的影响，而关于较长时间下经历环境老化载荷后柔性接头的研究几乎未曾报道。根据柔性接头成型特点及工作特性，本文基于内聚力模型建立了一种界面力学性能退化模型，以研究不同温度循环周期下的界面力学性能退化对柔性接头界面损伤的影响规律，为柔性接头老化研究提供参考。

2 柔性接头界面力学性能退化模型

本文基于双线性内聚力模型建立了界面力学性能退化模型。在损伤起始前，材料处于线弹性状态；当裂纹面间的分离量达到δ0或者应力达到tmax时，材料发生损伤；当分离量达到δmax时，材料完全失效。曲线与坐标轴围成的面积即为临界能量释放率，其中，GI C，GII C和GIII C分别对应I型、II型和III型裂纹的临界能量释放率。

损伤起始准则采用二次应力准则，可表示为

(1)

式中下标n，s和t分别对应法向、切向和环向。

实际过程中胶层所受载荷复杂，裂纹模式通常是由两种或更多基本裂纹模式相互叠加而成，本文采用BK准则来描述混合损伤演化过程。混合模式下的分离量δm可表示为

(2)

其中〈〉为MaxAuley算子，定义如下：

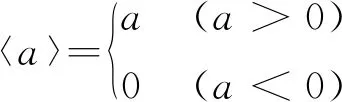
(3)

因此，混合模式下损伤起始分离量和完全失效分离量可分别表示为

(4)

(5)

损伤参数D定义为

(6)

式中δm,max为混合模式下的失效分离量，取，

δm,max=max.{min.{δm,max,δm,f},δm,0}

(7)

当δm,max≤δm,0时，胶层处于线弹性状态，根据式(7)知δm,max=δm,0，即有D=0，此时拉伸分离曲线可描述为

ti=Kδi

(i=n,s,t)(8)

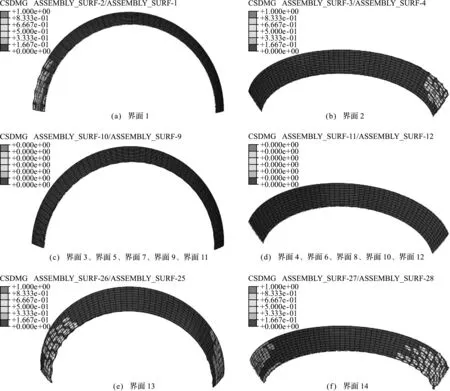
当δm,0<δm,max<δm,f时，胶层处于损伤演化阶段，根据式(7)，有0

ts=(1-D)Kδs，tt=(1-D)Kδt

(9)

当δm,f≤δm,max时，胶层完全失效，根据式(7)，δm,max=δm,f，即有D=1，此时拉伸分离曲线可描述为

(10)

式中μ为裂纹间的摩擦系数。

为反映界面力学性能参数随温度循环周期的变化关系，通过Liljedahl[25]的试验研究结果，引入界面退化参数Deg，建立一种界面力学性能退化模型。界面退化参数Deg可表示为

Deg=tk/t1

(11)

式中t1为第1组未经退化试验时胶层的粘接强度，tk为第k组经历(k-1)个温度循环周期后胶层的剩余强度。

界面的力学性能参数(包括初始刚度、断裂强度和临界能量释放率)均随界面退化参数呈线性退化，可表示为

Ki k=Ki×Degk(i=n,s,t)

ti k=ti×Degk(j=I,II,III)

Gj C k=Gj C×Degk(k=1,2,…,9)

(12)

根据文献[14]，表1列出了9组不同温度循环周期下某胶种的界面退化参数(温度循环范围为 -30 ℃～80 ℃，温度循环周期为2 h，该工况与固体火箭发动机工况基本相符)。

根据建立的界面力学性能退化模型，结合表2初始状态下胶层的力学性能参数[26]，可得到不同温度循环周期下胶层的内聚力模型参数，列入表3。

表1 不同循环温度周期下某胶种的环境退化参数Tab.1 Degradation parameter of adhesive at different temperature cycles

表2 初始状态下胶层内聚力模型参数Tab.2 Cohesive zone model parameters of adhesive in initial state

表3 不同温度循环周期下的内聚力模型参数Tab.3 Cohesive zone model parameters of adhesive at different temperature cycles

3 柔性接头有限元分析

3.1 柔性接头有限元模型

建立某一柔性接头模型如图1所示，其中弹性件共7层，每层沿周向划分50等份，宽度方向划分10等份，厚度方向划分3份；增强件共6层，每层沿周向划分50等份，宽度方向划分10等份，厚度方向划分2份。弹性件本构模型采用Yeoh模型，模型参数列入表4[27]，单元类型采用杂交单元C3D8H；增强件、前后法兰及摆杆为钢材料，材料参数列入表4，单元类型采用减缩积分单元C3D8R。

表4 材料参数

模拟时对称面采用对称边界条件ZSYMM，施加位移约束条件Z向位移U3=0；后法兰固定。对前法兰、堵盖及弹性件与增强件外表面施加压强来模拟容压；对摆心施加转角位移来模拟驱动载荷，具体过程为，在摆心处建立参考点，并将该参考点与摆杆耦合，对摆心施加位移约束U1=U2=U3=UR1=UR2=0，UR3按需要的摆角设置。同时，设置较小的载荷增量以保证计算结果的准确性。

3.2 界面损伤程度分析

为定量描述粘接界面的损伤程度，本文采用界面失效区域网格单元数与界面总网格单元数之比来定义界面的损伤程度，表达式为

DInterface=NF/NT

(13)

式中DInterface为界面损伤程度，NF为界面失效区域网格单元数，NT为界面总网格单元数。结合有限元计算结果，当界面上某网格单元损伤参数Di j≥0.95时，认为该单元失效，从而可得到界面失效区域的网格单元数NF，而在网格划分完成后即可得到界面总网格单元数NT。

从第一层弹性件到第七层弹性件各界面依次标号1～14，图2为6 MPa容压4°摆角下柔性接头粘接界面的损伤云图。可以看出，界面1、界面2、界面13和界面14均有损伤出现，且界面13和界面14的损伤区域面积分布较广，是最易发生粘接失效的界面；界面3、界面4、界面11和界面12上虽出现了微小损伤区域，但最大Di j值均小于 0.95，界面仅是局部微小区域产生了损伤，并未发生粘接失效。

图1 柔性接头有限元模型

图2 6 MPa容压4°摆角下柔性接头界面损伤云图

为定量描述各界面的损伤程度，图3显示了各界面在4°摆角下损伤程度随容压的变化趋势。

图3 4°摆角下不同容压各界面损伤程度

可以看出，各容压下界面14的损伤程度最大，界面13、界面1和界面2的损伤程度依次减小，而界面3到界面12未出现损伤。从损伤云图看，虽然界面3、界面4、界面11和界面12出现了损伤区域，但损伤区域内网格单元的损伤参数Di j均远低于0.95，因此这些损伤区域的单元并未发生失效。综上可得，柔性接头摆动时与后法兰粘接的界面损伤程度最大，靠近后法兰的第二层界面、与前法兰粘接的界面及靠近前法兰的第二层界面次之，中间界面无粘接失效产生。

由于任何一个界面密封失效都会导致柔性接头整体密封失效，因此界面14的损伤程度可以表征柔性接头的损伤程度。本文以界面14的损伤程度开展分析，图4显示了不同温度循环周期下，柔性接头界面14的损伤云图。可以看出，随着温度循环周期的增加，界面损伤区域面积变化并不明显，界面14上仅有一侧出现损伤区域；当温度循环周期增加到504次时，随着温度循环周期的增加界面损伤区域面积明显增加；当温度循环周期达到672次时，柔性接头的两端均出现了损伤。

为分析温度循环载荷对柔性接头各界面损伤程度的影响，图5为柔性接头界面的损伤程度随温度循环周期的变化关系。可以看出，界面1、界面2、界面13和界面14的损伤程度随温度循环周期的增加而逐渐增大；当温度循环周期达到672次时，界面13和界面14的损伤程度分别由初始状态的2.9%和4.3%增加到5.2%和8.2%，增幅分别高达81.2%和91.7%。同时，随着温度循环周期的增加，界面1和界面2损伤程度的增幅也越来越大。可见，界面损伤程度受温度循环载荷影响越来越严重，即温度循环载荷会加速柔性接头的界面损伤。

图5 界面损伤程度随温度循环周期的变化关系

该柔性接头在实际研制过程中曾出现过接头内外两侧界面密封失效的情况，这与本文计算得到的结论一致。证明了该界面力学性能退化模型的正确性，可为柔性接头老化研究提供参考。

4 结 论

本文基于内聚力模型建立了一种描述界面力学性能退化的数学模型，并以某柔性接头验证了该模型的有效性，得到以下结论。

(1) 该柔性接头工作时与后法兰粘接的界面损伤程度最大，靠近后法兰的第二层界面及与前法兰粘接的界面次之，中间界面无粘接失效产生。

(2) 柔性接头界面损伤程度随温度循环周期增加而逐渐增大，温度循环载荷会加速柔性接头的界面损伤。

(3) 该界面力学性能退化模型可为柔性接头老化研究提供参考。