椭球液滴撞击超疏水表面反弹过程数值分析

涂德浴， 潘庆民， 童宝宏

(安徽工业大学 机械工程学院，马鞍山 243032)

1 引 言

液滴撞击壁面问题广泛存在于自然界及工农业生产中，其过程细微且复杂，其中的流体动力学、热量和物质传输及控制等机理一直是众多专家学者们研究关注的领域[1]，如工业过程中的涂漆、抛光及表面处理等喷涂过程[2]，农业中对农作物施加肥料和喷洒农药[3]，以及机床和航空电子器件的喷雾冷却[4]等。针对液滴撞击壁面问题，国内外学者展开了大量研究。Andrade等[5]实验研究了不同液滴撞击甘蓝和香蕉皮表面，液滴发生不反弹、部分反弹和全部反弹等实验现象。Ding等[6]实验研究了液滴撞击不同温度的超疏水表面，探究了过冷度对液滴动力学行为及铺展系数等的影响。梁超等[7]通过VOF 方法模拟了相同速度的液滴撞击不同接触角固体平壁面上后形态特征及内部压力和速度场的变化。刘冬薇等[8]利用CLSVOF 方法模拟液滴撞击超疏水壁面过程中的反弹及破碎行为，得到了在一定条件液滴撞击超疏水壁面后发生反弹和破碎的临界条件。

液滴撞击过程中产生的二次液滴在许多场合会产生较大影响。李进等[9]仿真研究曲轴油箱内油滴撞击壁面过程，发现液滴粘度及表面张力越大，二次液滴产生越少。宋云超等[10]仿真研究了撞击速度及液体层等参数对液滴撞击湿润壁面时产生飞溅运动的影响，发现表面张力是二次液滴发生飞溅分离的主要作用力。范隆杰等[11]实验研究了高韦伯数下壁面温度对油滴撞击壁面过程射流高度及二次液滴的影响，发现随着韦伯数的增加，射流高度及产生的次级液滴数量也随之增加。

纵观液滴撞壁问题的研究发现，在实验和仿真模拟过程中均采用标准球形简化液滴形状，然而在实际工程应用中，液滴受实际因素影响会发生变形，使得液滴在撞击壁面时为非标准的球形，其中最常见的形变为椭球形[12-14]。然而目前有关形变液滴撞击壁面的研究较少。Yun等[15]利用环形电极产生不同形状的液滴，结合实验及数值模拟研究了液滴形态、撞击速度、壁面润湿性及We等物性参数对反弹高度的影响。随后进一步研究了韦伯数We及几何长纵比对椭球形液滴撞击热表面后反弹高度和接触时间的影响[16]，研究发现随着几何长纵比的增大，相同We的椭球液滴反弹最大高度逐渐降低，在AR约为1.8时，最大反弹高度达到饱和。裴传康等[17]采用数值模拟方法研究了5种不同高宽比椭球液滴撞击液池的过程，分析了椭球形变对气泡夹带的影响。

本文采用CLSVOF方法数值模拟了不同形变程度的椭球液滴撞击干壁面后的反弹过程，其中液滴拉伸变形方向垂直于碰撞表面，分析了形变程度对液滴的反弹过程及二次液滴产生的影响。进一步完善了对椭球液滴撞击壁面特性的理解，同时可为液滴的形态调控及喷嘴的设计提供理论参考。

2 数值计算模型及方法

2.1 控制方程

液滴撞击壁面属于复杂介质流动问题，描述这类流体介质运动时除了流体运动方程外，还需要考虑复杂的相间作用及相应物理因素的影响，在众多数值模拟方法中，VOF方法和Level Set方法应用较为广泛[18]。

VOF方法能够很好地保证质量守恒，准确捕捉界面拓扑结构的变化；但由于体积函数是离散量，准确求解较为困难。Level Set方法通过水平集函数来捕捉向界面变化，在计算曲率和法向量等几何参数上较为精确，这些参数是求解表面张力和进行界面重构的关键；但该方法并不守恒，计算过程中会造成质量的增加或减少。为了改善两种方法的不足，Sussman等[19]将Level Set方法和VOF方法进行了耦合，即CLSVOF方法。

·U=0

(1)

(2)

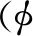
(3)

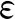
(4)

(5)

式中下标g和l分别表示气相和液相。

相界面平均曲率为

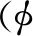
(6)

表面张力的求解采用Brackbill等[20]提出的连续表面张力模型

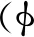
(7)

式中σ为表面张力系数。此方法既满足了流体流动时的质量守恒，又能确保界面几何参数的准确计算。

2.2 数值计算可行性验证

采用二维轴对称模型进行数值计算，液滴未变形时直径为2.13 mm，撞击速度为0.447 m/s，接触角取静态接触角160°。计算区域取5 mm× 5 mm，采用四边形均匀网格，压力速度耦合采用PISO方法，对Level Set方程通过有限体积法进行离散，采取QUICK格式，压力项采用PRESTO!格式，气液界面插值选择几何重构方法，动量求解采用二阶迎风格式。

图1(a)为由于设备振动而产生的椭球形液滴撞击壁面后的实验形态[21]，图1(b)为数值模拟结果。可以看出，液滴撞击固体壁面行为的数值模拟结果和实验结果较吻合。在液滴与固体表面碰撞铺展过程中，液滴与固体表面之间的接触角是不断变化的。因为许多工况下无法获得液滴与壁面间动态接触角的准确值，其次试验[22]测得2.25 mm液滴在超疏水壁面上前进及后退接触角与静态接触角相差均不超过5°，所以本文采用静态接触角。

图1 椭球液滴撞击壁面实验验证

2.3 数值模型建立

球形液滴受外力作用，会沿x轴方向压缩或拉伸为不同形态的椭球形，本文将相同体积时球形液滴的半径作为椭球液滴的等效半径re。此时椭球液滴沿x和y轴方向具有不对称性，半径分别为a和b, 根据体积相等，则有

(8，9)

为便于研究，定义不同轴向半径的比值为轴径比，AR=a/b。部分椭球液滴尺寸设计列入表1。

图2为AR=0.65椭球液滴撞击壁面初始时刻示意图，采取二维轴对称模型进行计算，其中x轴为计算域的对称轴，计算域大小为10 mm× 20 mm，其他相关参数列入表2。液滴刚和壁面发生接触为撞击初始时刻，空气和水均为不可压缩流体，环境压力保持1个标准大气压(101325 Pa)。

选取AR=0.65椭球液滴的面积分别为单元网格面积的2469，4380，6835，9835和13379倍的不同网格，验证网格无关性。计算结果表明细化网格对模拟结果有一定的改善，但是当网格精度增加到一定程度后对结果的影响已经不大。因此，下面的计算均采用AR=0.65椭球液滴面积为单元网格面积9835倍的网格。

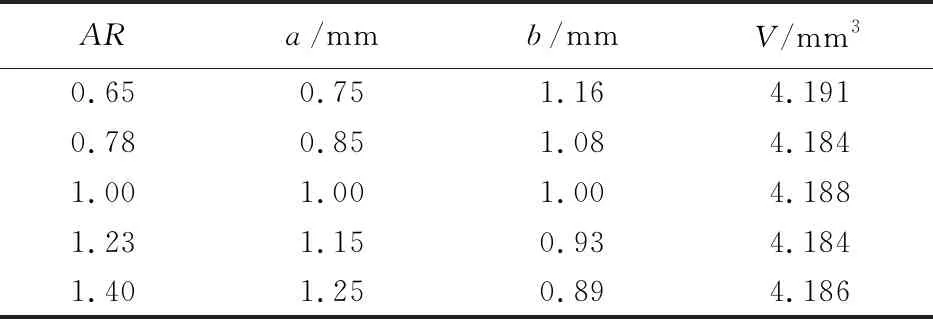
表1 部分椭球液滴尺寸

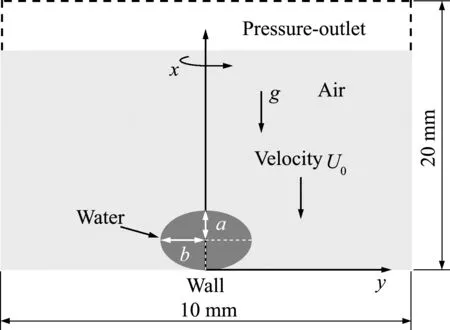
图2 初始时刻

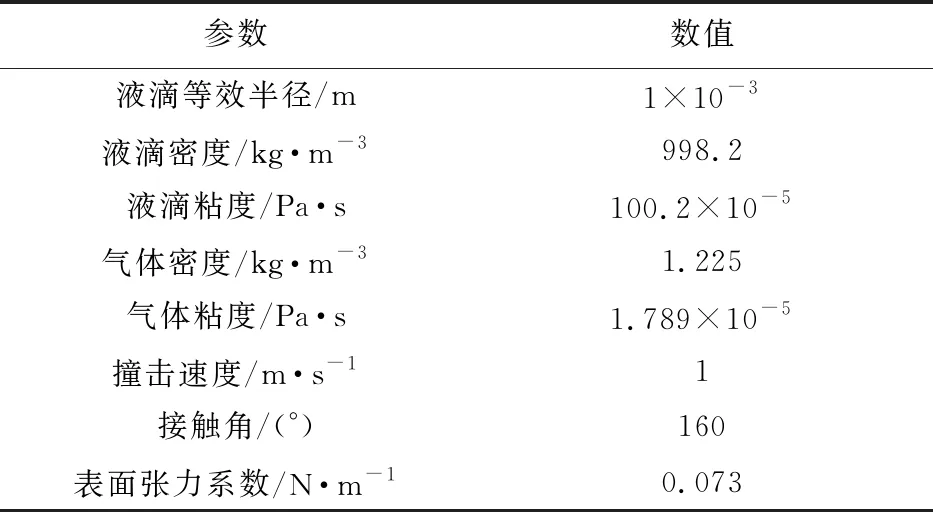
表2 计算参数

3 椭球液滴撞壁回缩反弹运动形态分析

3.1 椭球液滴撞击超疏水壁面回缩反弹特性

液滴撞击超疏水壁面后经历短暂铺展变化即达到最大铺展，由于壁面超疏水特性，液滴在铺展过程中能量损耗较小，使其具有足够的能量发生反弹[23]。图3给出了AR分别为0.65，1和1.23三种液滴撞击壁面后回缩及反弹过程中的形态，可以看出，不同AR液滴反弹过程具有一定相似性。 图3(b)球形液滴撞击壁面后，随着回缩运动的进行，不断受到表面张力及周围液体的挤压，液膜中心逐渐向上隆起(3.0 ms)；在表面张力和惯性力的持续作用下，液柱不断保持上升运动趋势，并逐渐拉伸呈图钉形(5.0 ms)；由于壁面的粘附作用，液滴底部并未离开表面，而液柱上方的自由液面继续向上运动，底部逐渐脱离壁面，并出现了液柱顶部断裂产生二次液滴的现象(10.0 ms)；二次液滴在断裂后以一定速度继续向上飞溅，由于韧带的断裂导致液滴在分离时具有瞬时冲量，表面形状在球形和椭球形间震荡[24]；液柱剩余部分在表面张力的作用下回缩成表面能较小的形态，但由于惯性力的影响并没有立刻变为球形而是呈左右对称的形态，并以类似蠕动的方式向上运动[25]。

可以看出不同AR液滴在反弹过程中存在明显的差异。首先，在3.0 ms时，AR=0.65液滴中心处聚集有更多的液体，且随着AR增加有明显减少的趋势；其次，5.0 ms时各液滴中心处均具有一定的液柱高度，但液柱的直径存在明显的差异；最后，AR=0.65液滴在10.0 ms时液柱顶端二次液滴恰好分离，而另外两种液滴产生二次液滴的时间均相对较早，AR=1.00和AR= 1.23 液滴产生二次液滴的时间分别为8.5 ms和6.2 ms。

图3 不同椭球液滴撞击超疏水壁面运动形态

3.2 AR对椭球液滴反弹过程中液柱的影响

图4为液柱顶点高度随时间变化规律，随着时间增加，液柱高度近似呈线性变化，且随着AR的增大曲线斜率逐渐增大。图4曲线初始横坐标代表长液柱形成时间，可以看出其随AR的增大而增大。其次，突起形态也明显不同，其直径大小随AR增大而减小。由液滴形成突起前的回缩过程可以看出，AR越小的液滴中心处在回缩过程中具有越厚的液体薄膜，使得外围液环在回缩过程中向上挤压的液体较多，造成突起较大。随后突起迅速向上发展，在5.0 ms时不同AR液滴均呈图钉状，但中心处形成的液柱具有明显不同的半径。

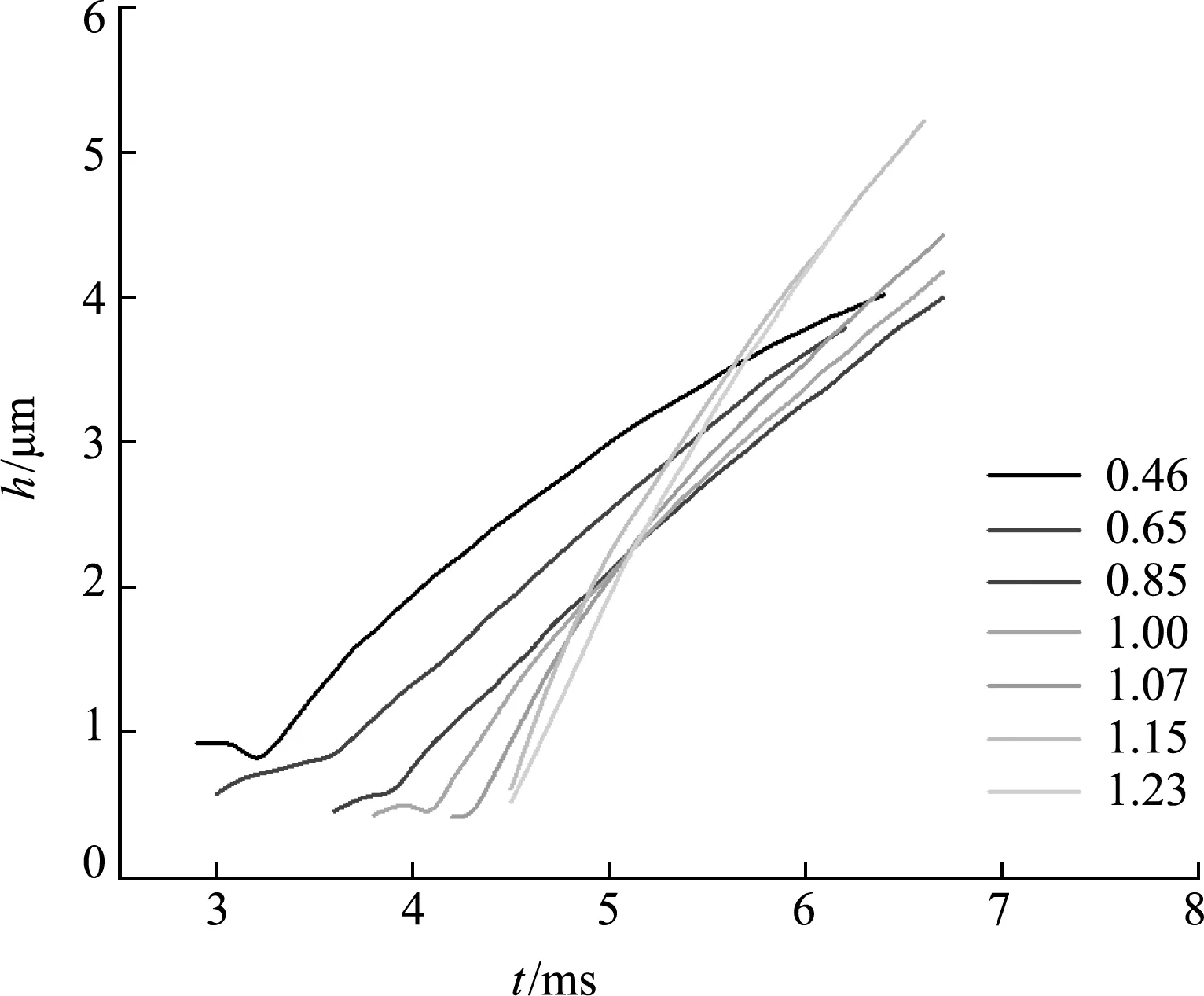
图4 液滴高度随时间的变化

图5为AR为液柱未扰动界面半径Rr随AR的变化，可以看出，随着AR的增大，Rr整体呈减小趋势。在一定范围内，AR越大，不同AR液滴撞击超疏水壁面后形成的长液柱越细长。由图3(c)可以看出较细长的液柱在6.7 ms时发生破碎，这是由于受Plateau-Rayleigh不稳定性作用的影响[26]，在5.0 ms时长液柱的末端出现明显凹陷，使得半径不均匀及半径较粗的地方呈外凸状，细的地方呈内凹状。由Young-Laplace方程可知，外凸状的曲率半径为正，对应的压力小；内凹状的曲率

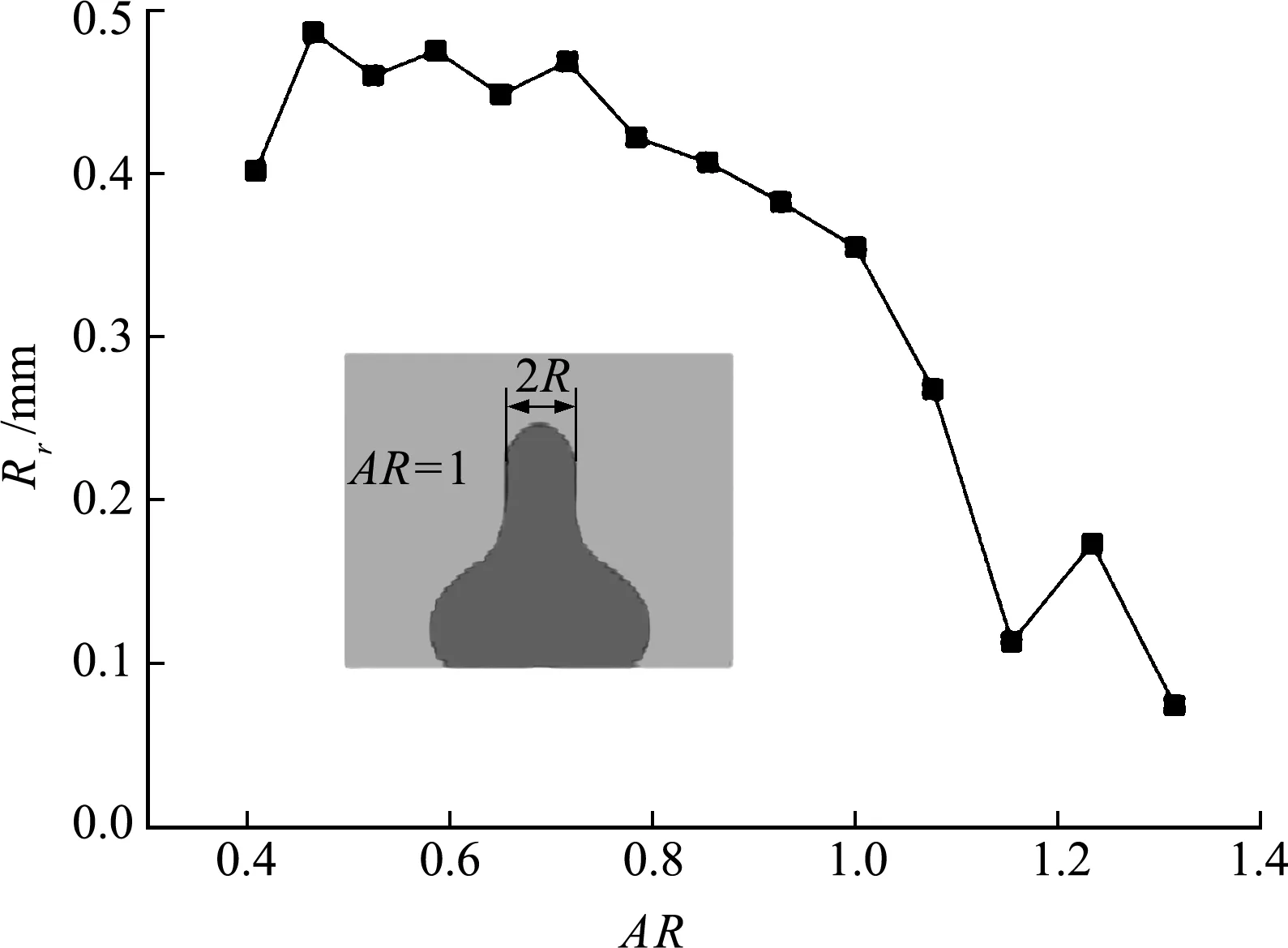
图5 液柱未出现扰动时初始半径

半径为负，对应的压力小，从而射流在轴向存在压力梯度。图6为液柱内部压力云图及速度矢量图。可以看出,轴向存在明显的压力梯度，且在颈部凹陷处附近压力最大。压力大的区域总是试图把液体挤向压力小的区域。从速度矢量图也可以看出轴向存在明显的速度梯度，在颈部凹陷处，液体向上流动的速度较快。因此，液体不断从水流细的地方挤向水流粗的地方，从而使细处越来越细，进一步加剧了不稳定性扰动的发展，最终在界面张力作用下破碎形成二次液滴。其中临界不稳定波长公式为

(10)

式中λ为临界波长，aL为颈部半径，当实际不稳定波长λa>λ时，则会有二次液滴产生[27]。图7为AR=1.15液滴在6 ms时颈部凹陷处形态，近似测量得到此时λa=3.295 μm，aL=0.077 μm，计算得λ=2.793 μm，即λa>λ，随后长液柱破裂产生二次液滴。

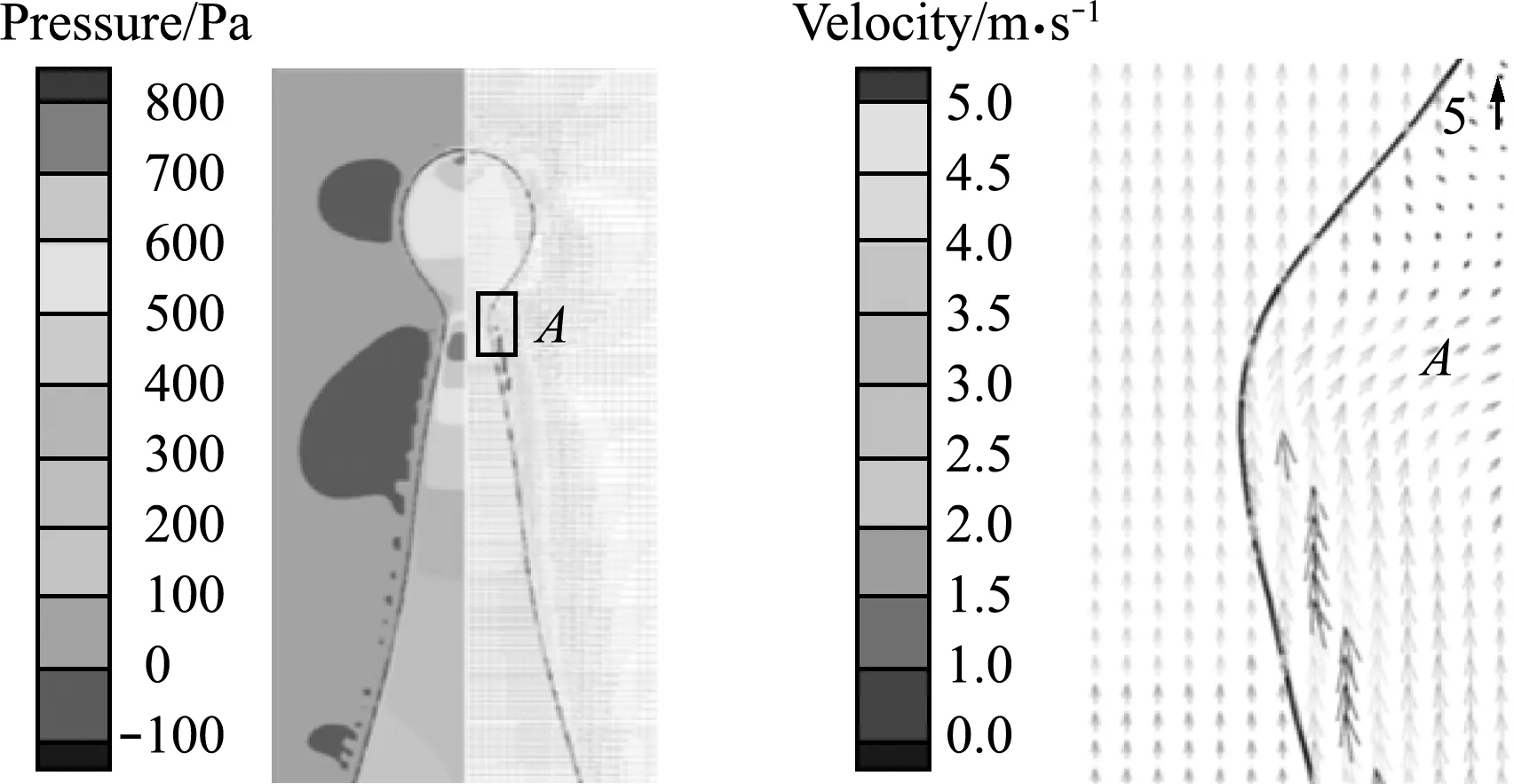
图6 液柱内部压力及速度分布

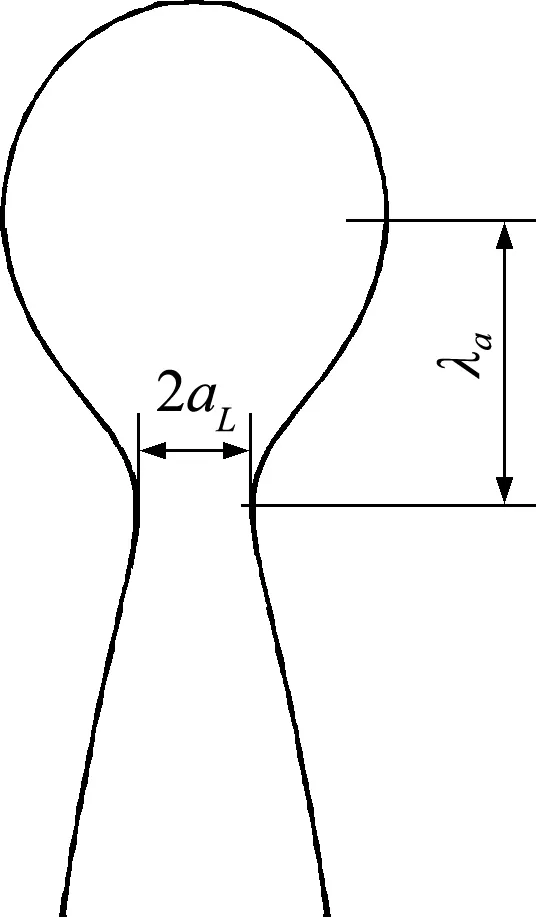
图7 AR =1.15液柱颈部

3.3 AR对椭球液滴反弹过程中二次液滴的影响

二次液滴的产生及相关特性对药物的滞留、分布及杀伤半径等会产生重要影响。图8为不同AR液滴撞击壁面后液柱破碎产生二次液滴的初始形态。可以看出，一定AR范围内的液滴撞击壁面后均在液柱的顶端产生二次液滴，并在破碎的初始时刻呈球形，但液柱的整体形态存在明显差异，当AR<1时，整个液滴经壁面反弹后在空中拉升为长液柱并破碎，液柱底部至壁面间距离及二次液滴产生时间均随AR的减小而增大，二次液滴的大小变化并不明显；而当AR>1时，二次液滴破碎的时间较早且直径明显减小。

图8 不同AR液滴产生二次液滴时形态

图9为不同AR液滴产生二次液滴的时间随AR的变化，可以看出,在一定范围内，液柱破碎产生二次液滴的时间随着AR增大而减小，较为特殊的是,当AR小于临界值0.6时，椭球液滴撞击超疏水壁面后无二次液滴产生。图10为AR=0.59液滴撞击壁面后的运动形态及内部压力云图。可以看出，在整个反弹过程中，由于液柱整体形态及内部压力分布较均匀，在12 ms时虽然可以观察到颈部的存在，该处压力略微增大，但并未发生断裂。在随后的运动中，液滴整体向上运动，但在惯性力及表面张力作用下，液滴整体形态存在震荡。

图9 二次液滴产生时间随AR变化

结合3.2节可知，在一定范围内，AR越大，液滴反弹过程中形成的液柱的直径相对较小，进而受不稳定影响也较显著，导致相应液滴在反弹过程中容易产生二次液滴。综上所述，在撞击超疏水表面过程中，较高的AR促进液滴反弹时二次液滴的产生，而较低的AR对二次液滴的产生存在明显的抑制作用，尤其是当AR小于临界值0.6时，反弹过程中不会出现二次液滴。

图10 AR =0.59液滴反弹形态及内部压力

4 结 论

(1) 椭球液滴撞击超疏水壁面后所经历过程及形态变化与球形液滴相似，均是先铺展达到最大半径，随后回缩并向上反弹形成长液柱，并会产生二次液滴破碎，但长液柱的形态及二次液滴产生的过程随AR的不同存在明显差异。

(2) 反弹过程中形成的长液柱，其开始形成的时间及向上发展的速度均随着AR的增大而增大，长液柱未发生扰动时，半径Rr随着AR的增大整体呈减小趋势，随后在Plateau-Rayleigh不稳定性作用下，长液柱发生二次液滴破碎。

(3) 二次液滴产生的时间及高度均随AR的增大而减小，较高的AR会促进液滴反弹时二次液滴的产生，而低AR对二次液滴存在明显的抑制作用，尤其是当AR小于临界值0.6时，反弹过程中不会出现二次液滴。