基于热固耦合问题的多尺度拓扑优化设计
魏兆栋, 高仁璟,2, 王长生*,2
(1.大连理工大学 汽车工程学院,工业装备结构分析国家重点实验室,大连 116024;2.大连理工大学 宁波研究院,宁波 315033)
1 引 言
拓扑优化是一种按照既定的设计要求和约束条件,在给定的设计区域内对材料分布进行优化的数学方法和工具,改变了依据经验和直觉的传统设计方法。随着理论研究的不断完善,拓扑优化的研究涉及到多学科多物理领域并取得了巨大的成果,如热传导[1-3]问题和静力学[4-6]问题等。然而在实际生产过程中,机械结构不仅承受外载荷,还经常面临高温的工作环境,因此考虑如何对这类结构进行合理拓扑优化是十分必要的。近些年来,利用逆均匀化方法按照优化意图对材料微结构进行优化设计来充分挖掘材料微结构的使用潜力受到关注,如何在材料微结构和宏观拓扑结构之间建立桥梁,充分发挥材料和结构的互补优势并应用到热固耦合结构问题是值得研究的热点。在微结构优化设计方面,Sigmund[7]首次采用逆均匀化方法,基于拓扑优化手段对复合材料的微结构极端性能进行研究设计,实现了泊松比在区间[-1,1]的微结构的最优设计,这项研究开启了设计具有特定弹性属性微结构的先河,此后又设计了具有极端热膨胀系数的三相材料微结构设计。Zhang等[8]以材料体积分数为约束条件,基于拓扑优化方法对复合材料极端热传导性能进行优化,获得在不同体分比下微结构的优化结果。以上文献是采用均匀化方法对材料微结构有效属性进行预测,针对预测材料等效属性问题,Xia等[9]提出了一种基于能量均匀化方法设计微结构的方法。Gao等[10]提出了三维的能量均匀化方法,并结合参数化水平集优化方法对三维微结构材料的弹性性能进行了拓扑优化设计。能量均匀化方法和渐进均匀化方法在预测微结构材料等效属性方面的结果是相似的,两者区别在于测试应变场处理,渐进均匀化方法的应变场是由单位测试应变场和由于单胞的非均质性引起的应变场叠加形成,而基于能量均匀化方法的应变场是由直接施加在边界上单位测试应变场引起的,在实际编程操作和公式推导中,能量均匀化方法对于处理微结构的周期性以及材料的应变场问题是比较清晰和简洁的,这也是本文选用该方法的考虑点。在多物理场耦合拓扑优化领域,Sigmund[11,12]研究了涉及电、热和机械等多物理场耦合时柔顺机构的拓扑设计方法。Deaton等[13]提出了基于应力约束的热固耦合结构拓扑优化模型。李冬梅等[14]提出了一种基于概率约束的可靠性热固耦合拓扑优化设计方法。Zuo等[15]探讨热固耦合场结构的控制方程,建立了基于SIMP法的耦合场拓扑模型。Gao等[16]基于双材料进行了质量约束下的热固耦合结构拓扑优化设计。Zhao等[17]建立了基于Ordered-RAMP模型的多材料插值模型,对热固耦合结构进行多材料拓扑优化设计,建立了综合散热弱度与结构柔度的多目标加权设计方案。占金青等[18]提出一种非均匀温度场下的热固耦合多相材料的拓扑优化设计方法,通过集成多相材料的方式来提升结构的性能。孟庆轩等[19]提出了一种在温度场均匀改变作用下的热固耦合结构应力约束拓扑优化方法。上述文献的优化尺度均停留在宏观结构方面,没有考虑材料微结构的优化层次,这对于充分发掘材料性能是一种损失。Anaya[20]基于渐进均匀化方法计算微结构的等效属性,同时结合双向进化结构优化方法(BESO)提出了一种多尺度热固耦合拓扑优化算法。与其相比,本文采用能量均匀化方法计算材料等效属性,并将其嵌入SIMP优化方法中建立一种热固耦合并行化优化方法,对于宏观结构的温度变化量的处理,本文不再将其设置为一个常数,而是依赖于离散单元节点的温度;此外进一步研究了该并行化优化方法对宏观结构位移和温度的影响,以期改善结构的力学性能。总体来说,针对热固耦合结构优化问题,如何利用拓扑优化手段且不使用优异性能材料以有效地改善结构的力学性能仍是目前研究的难点和热点。
本文提出一种基于稳态热源作用下的热固耦合结构多尺度拓扑优化设计,基于能量均匀化结合 SIMP插值方法建立并行化拓扑优化模型,以结构刚度作为目标函数,以材料体积分数作为约束条件,为了便于数值计算,利用直接法推导目标函数及约束的灵敏度,同时采用Heaviside非线性密度过滤技术抑制优化过程的数值不稳定现象,将OC准则用于优化问题求解。
2 热固耦合结构分析
对非均匀温度场下的热固耦合结构进行分析,温度场和结构场系统用有限元方程(1)进行描述:
(1)
式中Km和Kt分别为结构的整体刚度矩阵和热刚度矩阵,T为结构的温度向量,U为结构的位移向量,Ft为加载在结构上的热通量向量,Fm为结构所承受的机械外载,Fε为由于热应变产生的热载荷向量。
由文献[21]可知,结构受热膨胀引起的初始热应变ε0可表示为
ε0=αΔTΦT
(2)
式中α为材料的热膨胀系数,ΔT为单元温度变化量,在2D情形中,向量Φ=[1,1,0],3D问题中Φ=[1,1,1,0,0,0]。
由温度场变化产生的热载荷向量Fε表示为
(3)
式中N为离散单元的数目,B为单元的应变矩阵,D0为弹性矩阵。假设材料为各向同性,平面应力问题的弹性矩阵具体形式如下,
(4)

以2D问题为例,对式(3)展开得热载荷向量为
[-1-11-111-11]T
(5)

3 多尺度拓扑优化数学模型
利用拓扑优化技术结合能量均匀化方法,建立以结构刚度为优化目标的热固耦合并行化拓扑优化设计模型。将OC准则用于设计变量的迭代更新,即分别在每个尺度中进行设计变量的优化更新,利用能量均匀化计算每一次迭代后微结构拓扑的等效属性,使其作为两个尺度之间的连接桥梁,其对应的数学模型如下,
(i=1,2,…,NM;j=1,2,…,Nm)
s.t.α(uM,vM,DM)=l(vM), ∀vM∈H(ΩM,d)
α(um,vm,Dm)=l(vm), ∀vm∈H(Ωm,d)
(6)
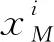
(7)
式中f为宏观结构的体力,h为宏观结构的Neumann边界ΓM上的牵引力。宏观和微观弹性张量DM和Dm可基于能量均匀化方法求解,根据修正的SIMP插值方法[4]定义如下,
(8)
式中为避免数值奇异,Emin为孔洞材料弹性模量,p为惩罚因子,根据相关文献,当p=3时能得到好的优化结果。DH为利用能量均匀化方法求得的弹性张量,
(9)
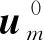
4 灵敏度分析
为了便于数值计算,利用有限元技术对式(6)的目标函数显式化,根据对热平衡方程和等效热载荷的分析,将刚度优化目标函数改写为
C=FTU=(Fm+Fε)TU
(10)
采用直接法[22]计算目标函数对宏观设计变量的敏度信息,同时结构外载荷Fm是一个确定常数,与设计变量无关,
(11)
以2D情形为例,∂Ft h/∂xM的求解具体如下,
[-1-11-111-11]T
(12)

对于离散单元的温度变化量处理如下,
(13)
式中ti为单元节点温度,n为离散单元的节点数,t0为参考温度,通常情况下取值为0。根据文献[23]描述单元节点温度ti表达如下,
(14)
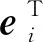
(15)
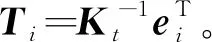
此时可以得出离散单元温度变化对设计变量的导数为
(16)
将式(12,16)代入式(11)整理得到2D情形的目标函数灵敏度,
(17)
式中ke为单元的刚度矩阵,ue为单元的位移向量。根据式(6)求解宏观设计变量的体积灵敏度,
(18)
对于微结构设计变量的目标灵敏度和体积灵敏度求解具体如下,
(19)
对于∂DH(xm)/∂xm的求解如下,
(20)
5 过滤技术及优化算法
为了获得清晰0/1离散分布的拓扑图并抑制宏微观尺度在优化过程中的数值不稳定现象,根据文献[24]采用Heaviside非线性密度过滤技术,修正后的单元密度为
(21)
式中引入一个正参数β来平滑Heaviside函数,同时
(22)
式中Ne为与单元e的质心距离小于过滤半径所有单元f的数目,权重系数He f具体如下,
He f=max.{0,rmin-dist(e,f)}
(23)
式中rmin为过滤半径,dist(e,f)为单元e和单元f的质心距离。
6 算例分析
通过对热固耦合并行化拓扑优化算例进行分析,验证本文方法拓扑优化的有效性。根据文献[9]可知,通常初始设计域由均匀分布的密度场组成,以避免出现局部最小值的设计,然而由于应用的周期边界条件将形成均匀分布的敏度场,不能持续更新变量,因此需要在微结构的初始设计域定义一些简单的空白区域,微结构的初始设计结构形状如图1所示。宏观结构的初始设计域长度和宽度分别设为40 cm和15 cm,离散为80×30的网格,设计域顶部施加均匀分布的发热热源,底边中点加载方向向下的集中载荷,左右两边界固定且绝热,同时底边温度设置为0 ℃,具体载荷和边界条件如图2所示。微结构划分为50×50的网格,每一个微结构的尺寸均为5 mm,微结构的尺寸远小于宏观结构的尺寸,符合均匀化理论的要求。过滤半径设置为1.4,其余设计参数列入表1。
该算例的停止准则定义为优化迭代步数不小于100步且相邻迭代的宏微观设计变量最大差值的绝对值均不超过0.05。

图1 微结构初始设计形状
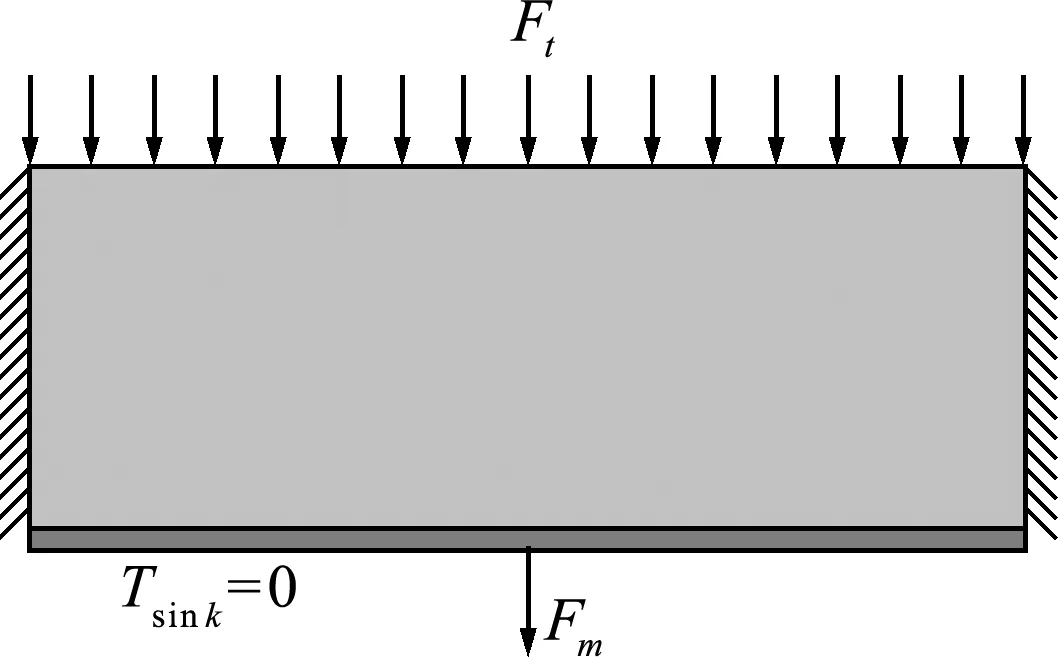
图2 结构载荷及约束条件
图3给出并行化拓扑优化结构和微结构的弹性张量矩阵和热传导系数矩阵;图4为非并行化和并行化拓扑优化的优化迭代图,由于微观拓扑在优化过程计算得到微结构的等效材料属性的精度问题导致并行化优化过程中出现几次波动,但不影响最终的稳定性。为了验证所提出的优化方法能够有效地提高结构的刚度性能和散热性能,给出并行化拓扑优化和非并行化拓扑优化对于宏观结构在x和y方向的位移以及结构温度分布的对比云图,如图5所示,左侧为并行化拓扑优化的结果,右侧为非并行化的情况,可知非并行化情况下结构的最高温度大约在4 ℃~5 ℃,沿x方向的最大位移在0.1 cm~0.15 cm,沿y方向的最大位移大于 1 cm;然而经过并行化处理之后的热固耦合结构的最高温度为0.3 ℃,在x方向位移大约2.5×10-3cm~3×10-3cm,沿y方向最大位移约为 0.025 cm,数据结果表明,并行化处理之后,结构的温度分布和位移形变得到大幅度的降低,由此可知所提出的优化方法能够显著改善结构刚度性能和散热性能。
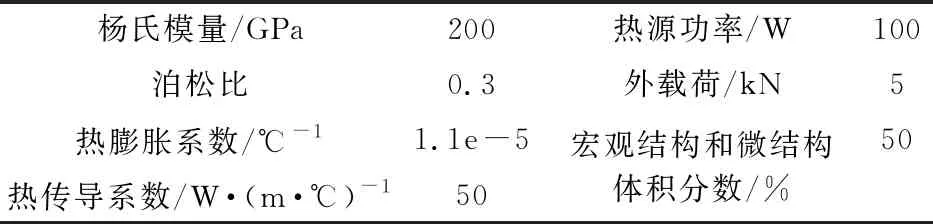
表1 优化参数
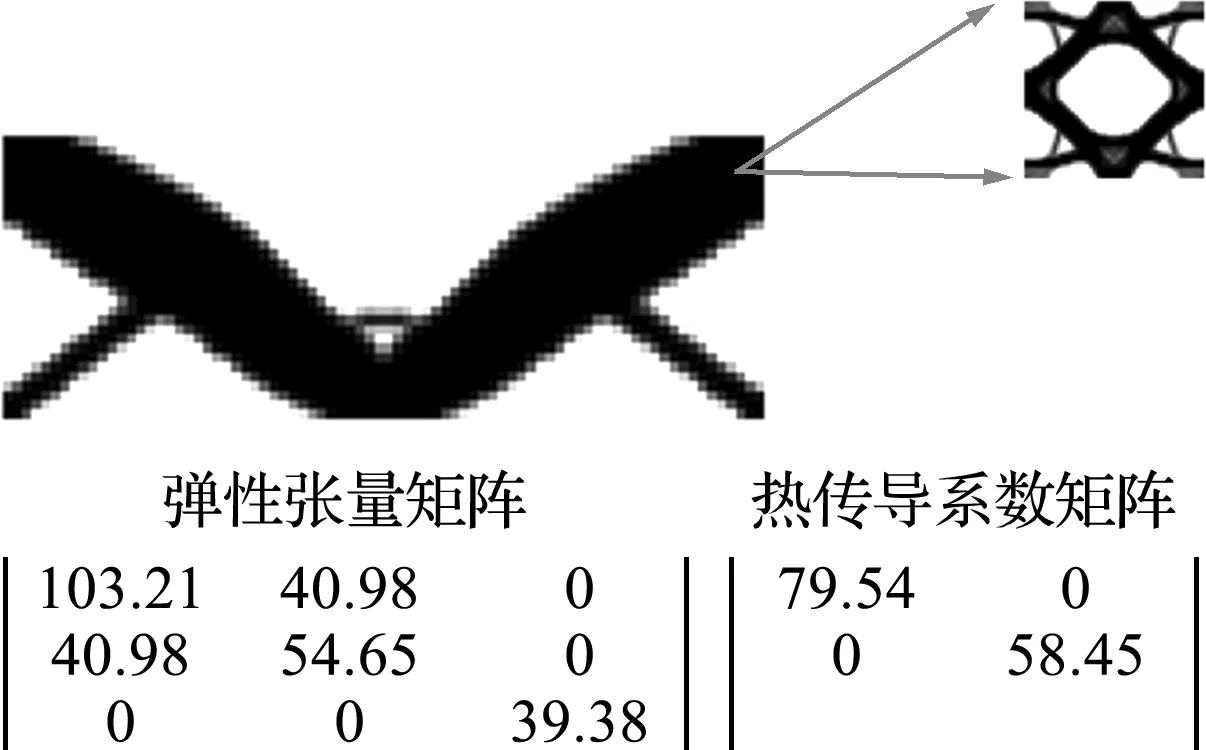
图3 2D并行化拓扑优化结果

图4 拓扑优化迭代
在2D的基础上开展3D情形的拓扑优化设计,三维悬臂梁的载荷、约束条件以及微结构的初始设计结构如图6所示,结构场的右边界固定约束,左边界底边施加向下的力,温度场顶部施加均匀分布热源,底部温度设置为0 ℃。宏观结构的尺寸为30 cm×10 cm×1 cm,划分为60×20×2单元;微结构尺寸为5 mm×5 mm×5 mm,划分为 10×10×10单元。为了能够进行微观尺度的设计变量更新,将微结构的内部中心删除2×2×2个单元。算例过滤半径设置为1.5,其余优化设计参数列入表2。
该算例的停止准则定义为优化迭代步数不小于100步,且相邻迭代的宏微观设计变量最大差值的绝对值均不超过0.02。
图7展示了3D情形的并行化拓扑结构,包括微结构的弹性张量矩阵以及热传导系数矩阵。图8 是并行化优化过程迭代图。由于并行化的缘故,宏观结构的拓扑形状对比于非并行化的拓扑结构有很大改变,如图9所示。微结构整体上是有两块直板构成,中间没有材料连接的结构,但是如果将材料的弹性模量和热传导系数增大,如弹性模量设置为10 GPa,热传导系数设置为10 W/(m·℃),其余优化参数不变,具体优化结果如图10所示。对比图7的拓扑结构,宏观结构和微结构有很大的变化,由于提高了材料的力学属性,宏观拓扑结构明显少了一些分支,同时微结构的中间部分有材料连接,因此改变材料参数会使得结构的拓扑形状发生较大的变化,侧面说明了所提出的优化设计方法能够有效地进行优化设计。
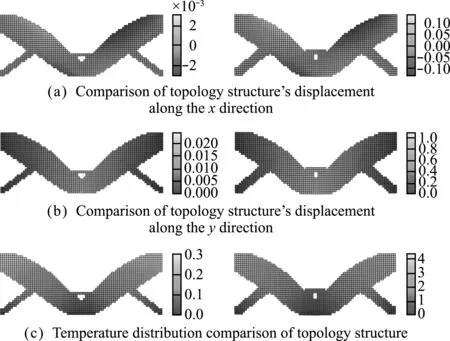
图5 并行化拓扑优化与非并行化的结果对比

表2 优化参数
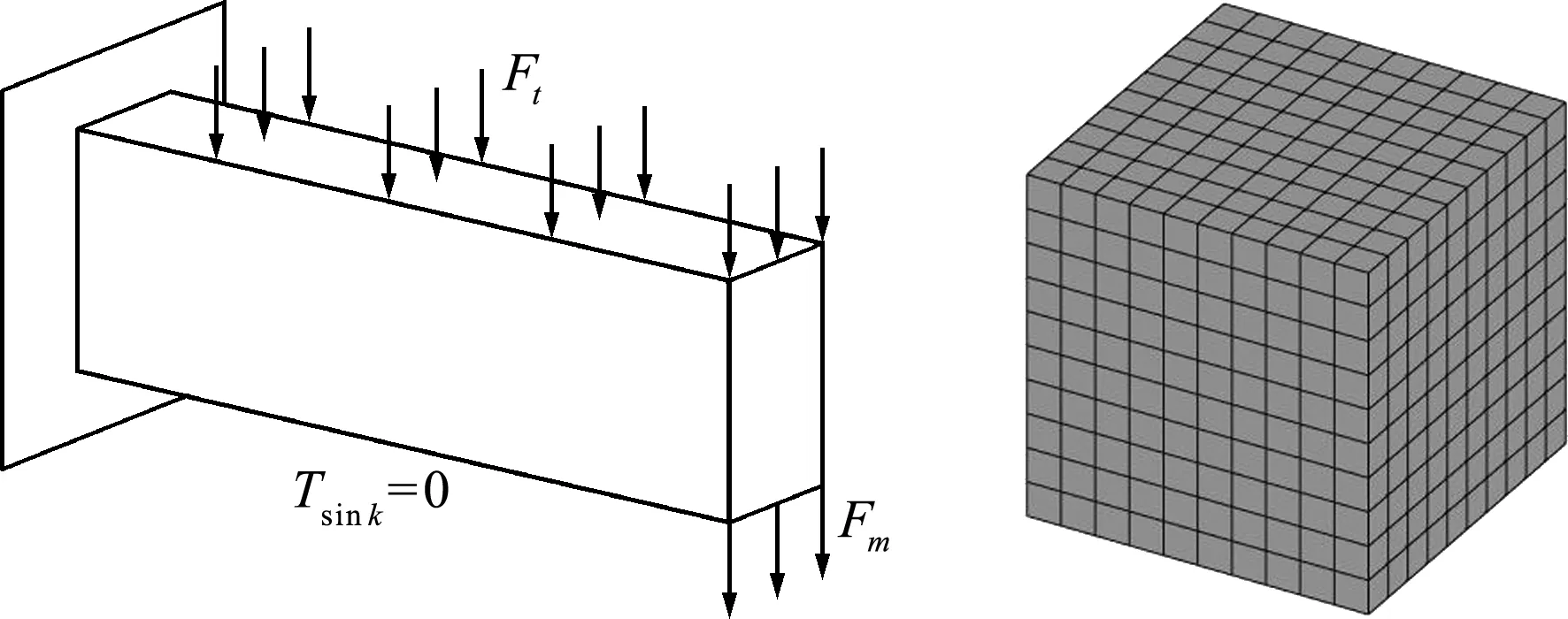
图6 悬臂梁载荷和约束条件以及微结构初始结构
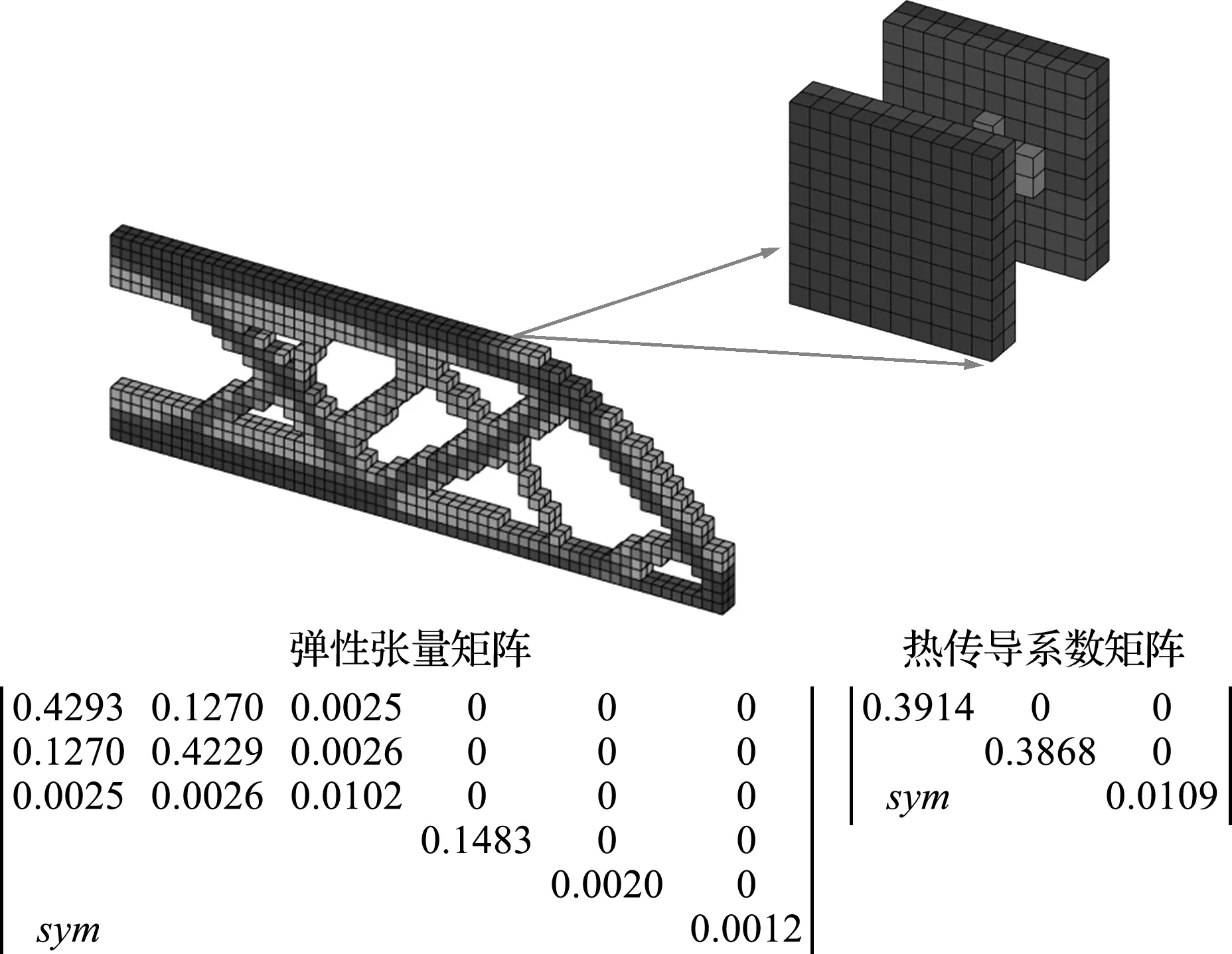
图7 3D并行化拓扑优化结果
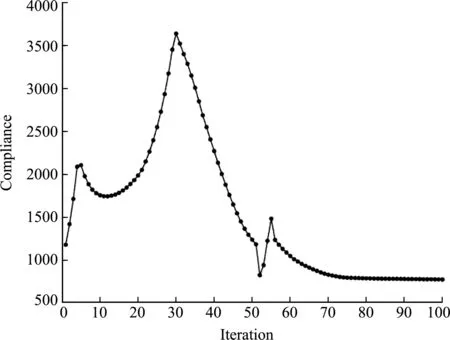
图8 3D并行化优化迭代
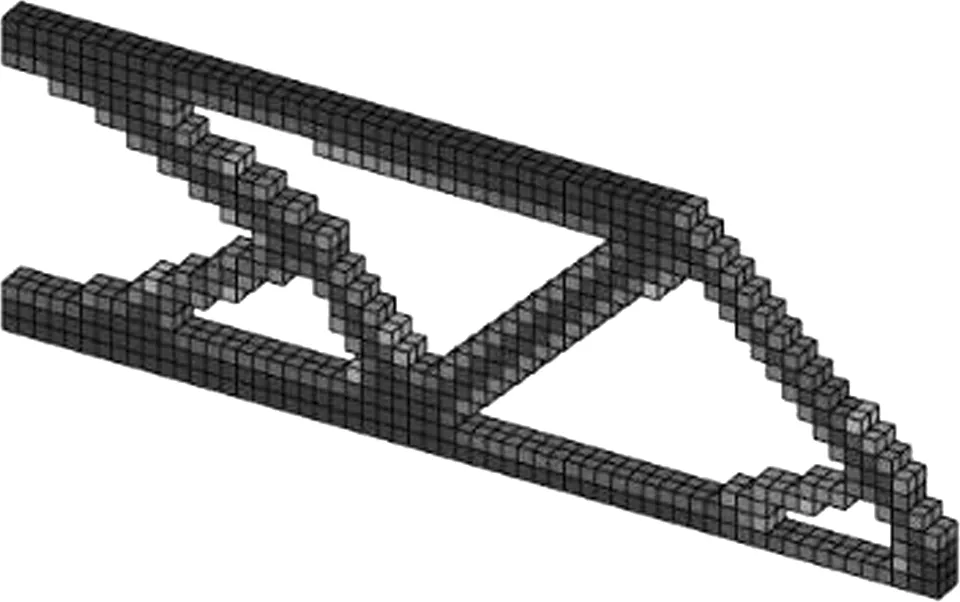
图9 非并行化宏观拓扑结构
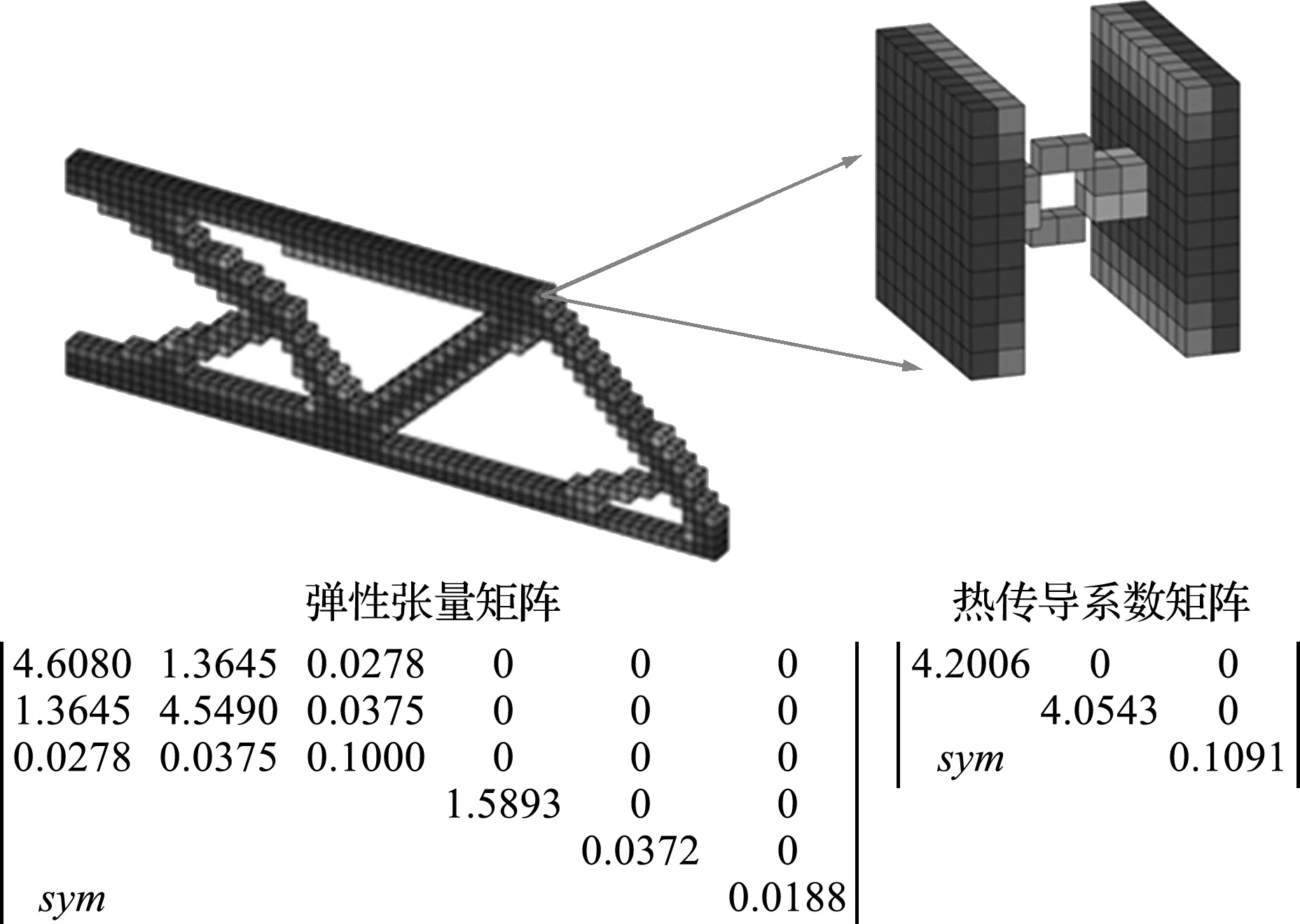
图10 并行化拓扑优化结果
7 总 结
本文利用能量均匀化方法结合拓扑优化技术建立了基于稳态热源作用下的热固耦合结构多尺度拓扑优化设计模型,以结构刚度为优化目标,体分比为约束,通过开展2D和3D的典型数值算例优化设计,验证了所提出的优化方法能够有效地进行优化设计,并且通过与非并行化热固耦合拓扑优化做对比,证明了该优化方法能够显著地改善结构的刚度性能和散热性能,顺应了现代化生产对工业产品高强度轻量化的设计趋势,为基于多物理场耦合问题下开展结构/材料多尺度一体化拓扑优化设计提供了一定的参考价值和指导意义。

