600Wh 飞轮转子形状优化设计

任正义，赫 鹏，杨立平

（1.哈尔滨工程大学工程训练国家级实验教学示范中心，黑龙江 哈尔滨 150001；2.哈尔滨工程大学机电工程学院，黑龙江 哈尔滨 150001；2.哈尔滨工程大学储能技术与应用研究所，黑龙江 哈尔滨 150001）

1 引言

随着社会的飞速发展，人们对生活水平的要求越来越高，社会工业化和信息化和能源紧缺的问题成为发展的主要矛盾，人们不得不更多的关注可再生能源与能源储存的问题。飞轮电池具有充电时长短，储能密度高，寿命长，无污染以及能量转换率高等优点成为研究热点[1]。对于飞轮主要的设计要求是在满足应力应变要求的同时以质量更轻，储能密度更大目标。文献[2]采用有限元法，通过优化飞轮转子的形状减少了应力集中。文献[3]基于并行遗传算法，以提高飞轮储能密度为目标进行了研究。文献[4]采用有限元和拉格朗日乘子法，对飞轮进行了形状优化，是飞轮储能密度显著提高。文献[5]采取差异演变算法对高速旋转的金属轮毂进行了形状优化。目前对于飞轮转子的优化主要使用的算法由渐进结构优化法、ICM 方法、ESO 法以及遗传算法等优化设计方法[6]。

基于多目标遗传算法和有限元分析，针对600Wh 的空心飞轮转子，以减少质量，提高储能密度为目标，进行结构分析与优化设计，寻找最优的空心飞轮转子形状与设计参数。

2 飞轮转子系统组成

飞轮转子系统主要由电机、飞轮转子、推力盘、径向电磁轴承和轴向电磁轴承以及保护轴承组成[7]。主要结构，如图1 所示。

图1 飞轮转子系统结构Fig.1 Flywheel Rotor System Structure

飞轮储能的原理是利用径向轴向轴承将飞轮轴系进行稳定悬浮，由电机带动飞轮进行高速转动，将能量储存在高速旋转的飞轮中，发电时，飞轮带动发电机高速旋转进行释能，从而实现电能与动能的相互转换。

针对600Wh 飞轮储能系统进行研究，飞轮转子是储能系统的核心，极限转速为15000rpm。

3 飞轮转子数学模型分析

3.1 飞轮储能量和储能密度分析

飞轮储能系统的储能量表达式是

式中：J—转动惯量；ω—飞轮转速。

对于飞轮系统提高储能量有俩种方法：1 提高飞轮转速2 增大飞轮转动惯量

储能密度主要分为三种，分别为质量储能密度，体积储能密度和成本储能密度，一般常用的是质量储能密度，所以使用质量储能密度进行分析。

质量储能飞轮密度及其表达式为[8]：

式中：m—飞轮质量；Ke—飞轮形状系数（与飞轮材料、应力分布、结构形状有关）；［σ］—飞轮材料需用应力；ρ—飞轮材料密度。

3.2 储能指标参数分析

分析对象是600kWh 飞轮转子系统，其设计要求为：储能量E=600kWh；工作转速（5000～15000）r/min；放电深度λ=8/9；飞轮储能总效率η=90%。

飞轮在极限工作状态下工作时，系统储能量为：

式中：R0—飞轮的有效回转半径。

根据600Wh 飞轮储能的设计以及安装要求，得到飞轮结构，如图2 所示。

图2 飞轮结构形式Fig.2 Flywheel Structure

3.3 飞轮转子应力分析

在储能系统最大转速和材料确定的情况下，高速转动的飞轮转子主要承受离心力，可以分成径向应力和周向应力。空心等厚盘形飞轮的应力计算公式为[7]：

式中ρ—材料密度；μ—泊松系数；r—飞轮内径；R—飞轮外径；ri—飞轮上某点的半径；ω—飞轮角速度。

根据工程设计Tresca 屈服准则，有：

式中：［σ］—飞轮材料的许用应力。

4 基于遗传算法的飞轮优化分析

4.1 盘式轮辐式飞轮转子模型有限元分析

由于空心飞轮转子与实心相比质量更轻，转动惯量更大，所以目前常用的飞轮转子多为空心飞轮转子。600Wh 飞轮转子原采用的是盘式轮辐式空心飞轮转子，设计参数，如表1 所示。

表1 盘式轮辐式设计参数表Tabl.1 Disc Spoke Design Parameters

按照表中所给的设计参数，使用三维软件SolidWorks 进行建模，得到初始模型，如图3 所示。

图3 原模型Fig.3 Original Model

将其导入Ansys Workbench 中进行有限元分析，可得其最大应力应变，如图4、图5 所示。

图4 原模型应力图Fig.4 Original Model Stress Map

图5 原模型应变图Fig.5 Original Model Strain Map

得到的初始模型盘式轮辐式模型的最大应力应变分别为515.55MPa，0.52988mm，极转动惯量为9.0088e+05kg·mm。

4.2 优化模型的建立

通过将盘式轮辐式飞轮改成曲线轮辐式飞轮进行分析，首先设定曲线为半圆形，进行初步分析建模，如图6 所示。

图6 半圆轮辐模型Fig 6 Semi-Circular Spoke Model

将其导入ansys workbench 中进行静力分析可知，应力集中位置位于轮辐接触处。

通过对接触处不同大小的倒角来进行减小接触处应力集中，将倒角分别设置为10mm，15mm，20mm，观察倒角减小的最大应力变化趋势和应力集中的位置变化，分析结果，如图7～图9所示。

图7 10mm 应力应变图Fig.7 10mm Stress Strain Diagram

图8 15mm 应力应变图Fig.8 15mm Stress Strain Diagram

图9 20mm 应力应变图Fig.9 20mm Stress Strain Diagram

通过观察应力应变的分析结果可以改变倒角的大小后应边并无明显变化，但是应力会有明显减小的趋势，并且在倒角增大到一定程度下，应力集中逐渐从轮缘轮辐连接处向内径凸台附近转移并增大，并且转动惯量也随之增大。因而通过综合考虑飞轮的转动惯量与应力变化，以及追求比原模型转动惯量更大，质量更轻，以及应力减小的设计要求，最终建立飞轮优化的初步模型，如图10 所示。将原来的半圆型变成俩圆曲线相交相交，凸台内侧的圆直径P10为100mm，外侧圆半径P9为70mm，倒角P3为20mm。

图10 优化初步模型Fig.10 Optimization Preliminary Model

4.3 基于遗传算法飞轮优化的有限元求解

遗传算法通过效仿生物界的进化规律和达尔文适者生存，优胜劣汰的遗传机理演化而来的随机探索方法，是一种采用模拟自然进化规律探索最优解的方法[9]将优化的初步模型进行静力学分析，得到其应力应变，提取飞轮P3、P9和P10为设计变量，将其应力P4、应变P5，转动惯量P8以及质量P7参数化，设置其约束，寻找最优质量，优化参数、约束参数以及目标参数范围设置，如图11、图12 所示。然后设置其优化方式，选择MOGA 算法，进行多目标遗传算法优化，初始样本数量100，迭代10 次。然后通过遗传算法，进行优化求解，多目标约束下解除其最优的方案，优化过程大约持续20 个小时，共算的99 组方案。最终给出了三种最优设计变量的参数，通过查看候选名单，找出三种最适合的候选方案，如图13 所示。

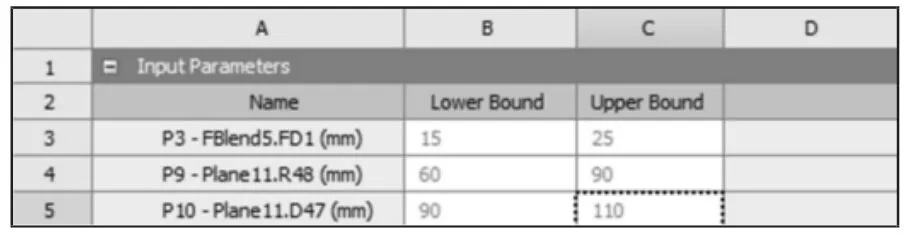
图11 变量参数范围Fig.11 Variable Parameter Range

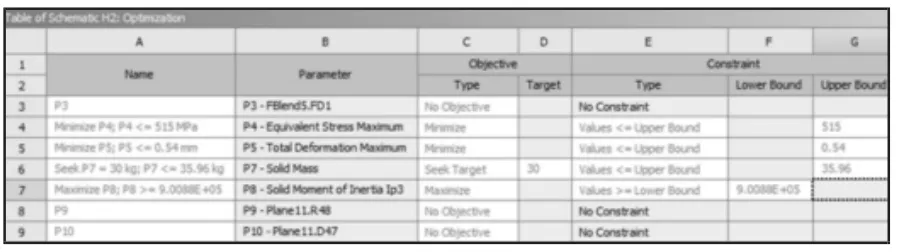
图12 约束参数设置Fig.12 Constraint Parameter Settings

图13 候选方案Fig.13 Candidate Solution

优化设计后的得到其三维权衡图以及输入变量的敏感度，如图14、图15 所示。

图14 三维权衡图Fig.14 Three-Dimensional Trade-off Diagram

图15 输入变量的敏感度Fig.15 Sensitivity of Input Variables

这些参数对优化设计有不同的影响，分别对三种方案进行再分析，将得到的候选方案参数分别作为设计点进行输入，得到三种方案的输出参数以及最大应力应变图，如图16～图18 所示。

图16 候选点1 输出变量及其应力应变图Fig.16 Candidate Point 1 Output Variable and its Stress-Strain Diagram

图17 候选点2 输出变量及其应力应变图Fig.17 Candidate 2 Output Variable and its Stress-Strain Diagram

图18 候选点3 输出变量及其应力应变图Fig.18 Candidate Point 3 Output Variable and its Stress-Strain Diagram

通过分析三组优化方案的输出变量及其应力应变图可发现，三种方案对比原方案在质量，转动惯量以及应力上有不同程度的优化，应变仅有微小的增加。其中，方案一应力减少7.6%，应变增加0.17%，质量减少百分之0.31%，极转动惯量增加0.1%。方案二应力减小6.8%，应变增加0.15%，质量减小0.3%，极转动惯量增加0.08%。方案三应力减少4.7%，应变增加0.26%，质量基本未变，极转动惯量增加0.27%。综上所述，方案一在应力减小明显，在其他方面也更有优势。

5 结论

（1）对半圆轮辐形飞轮进行了圆倒角分析，发现当倒角增大时轮辐轮毂接触处的应力明显减小，应力集中向内径凸台附近转移。（2）通过采用遗传算法进行优化设计，得到了一种新型结构的飞轮设计参数，使得飞轮最大应力明显减小，并在其他方面也略有改善。