并联机器人正运动学与NURBS 轨迹规划

张皓宇，刘晓伟，任 川，赵 彬

（1.辽宁省气象信息中心，辽宁 沈阳 110168；2.沈阳新松系统自动化股份有限公司，辽宁 沈阳 110168；3.东北大学信息科学与工程学院，辽宁 沈阳 110819）

1 引言

并联机构学理论研究蓬勃发展，并联机器人的运动学理论也不断得到丰富[1-3]。并联机器人是一种具有高载荷自重比的封闭式运动结构，适用于制造、飞行仿真系统和医疗机器人等领域。机械手是一组运动连杆或链条的集合，这些连杆或链条连接在一起形成一个能够完成特定任务的机构[4]。典型的任务包括取放操作、模仿人类动作和在危险区域操作。机器人具有两种基本设计，串联和并联，在运动学上是不同的。串联式机械手是由一系列端到端的运动环节连接而成的开环结构，代表了当今大多数结构类似于人类手臂的机器人机械手[5]。并联机器人又称并联机器人、并联机器人是一种闭环运动结构。一般来说串联机器人正运动学求解容易，逆运动学相对较难。虽然串行机械手由于其开环运动结构，易于理解，但不适用于快速分拣、小范围搬运等场合。并联机器人逆运动学求解容易，正运动学处理很难有通用解决办法。机械上，并联机器人由带有末端执行器的移动平台组成，末端执行器通过三个或更多的铰接链接连接到基座，每个链路在链路基座附近都有一个线性驱动器。并联机器人都很适合这些快速高自重比的应用，在最终定位的末端执行器提供了更高的精度。

任何串行或并联机器人都存在两类运动学问题：逆运动学问题（IKP）和正运动学问题（FKP）[6]。目前的FKP 求解策略依赖于迭代方法，迭代方法计算开销大，耗时长，且不能进行最优的实时操作。针对FKP 问题，提出了一种利用改进形式的多层感知器进行反向传播学习的神经网络将问题的求解精度提高到预期水平，并能实时求解。再次，研究了建立NURBS 曲线相关步骤相关技术，建立了NURBS 曲线并将其运用到并联机器人轨迹插补中，它可以处理任何类型的几何图形。NURBS 分段点定义为加速度在零方向上变化的过渡点。求解了运动学和NURBS 曲线问题，建立机构的位置、速度、加速度与连杆长度、角度等机构参数之间的关系，为后续并联机器人快速分拣提供了保障。

2 机械臂构成

工业机器人传统上是一种开链的机构，其连杆通常是串联的[7-8]。开放式运动链机器人通常具有较长的臂长、较大的工作空间和较好的机动性能。然而，悬臂式机械手本身的刚性较差，在高速、高动载工况下的动态性能较差。而并联机器人特别是自动装配，快速分拣，高自重比和高精密机械加工工装夹具组装就显得尤为重要，也是研发人员一直努力寻找的有效解决方案。

并联机器人机构图，如图1 所示。基于闭合运动链概念的可选机械手设计研究取得了一定的进展，与传统的开放式运动链机械手相比，具有以下优点：由于缺少悬臂式结构，使得刚性和精度更高，对于执行机构的数量具有较高的力/扭矩能力，因为执行机构是并联而不是串联布置的，而且逆运动学相对简单，这是实时计算机在线控制的优势。闭环运动链机器人在工作空间和可操作性要求低、动载荷大具有广阔的应用前景。

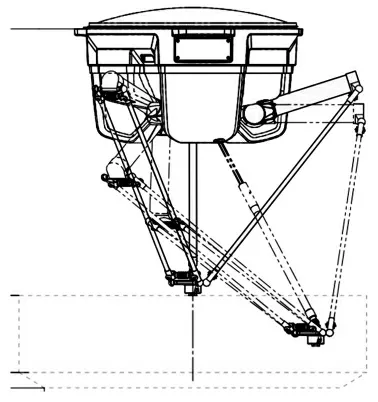
图1 并联机器人机构图Fig.1 Mechanism Diagram of Parallel Robot

3 机械臂运动学分析

并联机器人正解解决的是从机器人关节到机器人末端姿态的传递关系，反解解决的是从机器人末端姿态到机器人关节角的传递关系，正反解是解决机器人在空间运动的关节角和空间位姿的传递关系。在数学上，虽然并联机器人的IKP 有一个封闭的数学解，但是FKP 缺少一个封闭的解[9-10]。一般来说，FKP 表示一个待定问题，其中方程的数量小于未知数的数量。此外，运动学公式的高度非线性也增加了计算的复杂性。IKP 将任务空间映射到关节空间，根据机械手的最终位置和方向，找到关节角度或连杆长度。在数学上，IKP 建立了这样一个映射函数：｛task space｝｛joint space｝。FKP 将关节空间映射到任务空间，根据给定的关节角度或长度集找到最终的位置和方向。FKP 的求解需要完成运动控制系统的反馈回路，即FKP 指示是否已经到达工作区中所需的点。目前的FKP 求解策略依赖于迭代方法，迭代方法计算开销大，耗时长，且不能进行最优的实时操作。

3.1 机械臂运动学反解

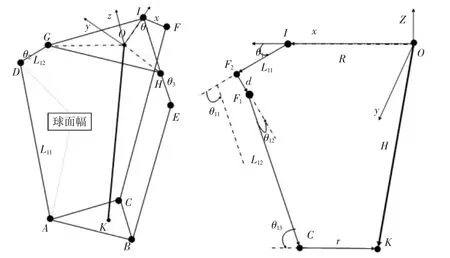
图2 第i 分支的关节角和杆长的示意图Fig.2 Schematic Diagram of Joint Angle and Bar Length of Branch i

图中：（xk，yk，zk）—o-xyz坐标系中的物理坐标；r—动平台的外接圆半径；R—固定平台的外接圆半径；i、θij—第i支链上的第j杆的杆长和转角。

首先，F1和F2组成一个球形副，所以：首先，沿y轴平移L12；然后，绕x轴旋转θ12；最后，绕y轴旋转（θ1+θ11-90°），整理得：

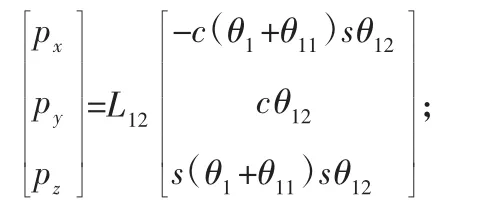
设末端执行器中心的坐标为（xtcp ytcp ztcp），这样可以获得位置变换的坐标公式：

3.1.1 消元法反解

求解θ1，整理方程式：

3.1.2 归一解

根据上面第一支链的结论，可以得到并联机器人运动学反解的归一解（通用解）：

3.3 机械臂运动学正解

目前并联机器人正解析解决办法有几类方法：分析方法、迭代方法、使用额外的传感器和神经网络的方法[11-13]。在并联机械手末端安装额外的传感器，以获得更多关于系统（机械手）状态的信息，有助于快速方便地解决FKP。传感器的额外成本使得这成为解决FKP 最不理想的方法。在迭代方法中，运动学问题被公式化，因此它可以使用任何可用的数值技术来求解。然而，这些数值技术是计算密集型的，并不能保证一个解决方案。本节介绍了一些并联机器人构型的神经网络求解FKP 方案。神经网络正运动学的目标是设计一种方法，适用于所有类别的并联机器人，减少计算资源的使用、实时快速执行。

3.3.1 神经网络概述

基于神经网络求解FKP 的分析方法不仅限于并联机器人的特殊结构，可以推广到其他类型的并联机器人。神经元处理单元对修改后的信号进行求和，并将该值应用于线性或非线性激活函数。然后，产生的信号或值被传送到输出单元。输入、权重、体系结构和阈值都是神经网络器可以控制的参数。

一旦确定了神经网络的体系结构，就可以通过训练或学习过程来设置权重值。在网络训练中，神经网络的自由参数（权值）是通过环境的连续刺激过程来适应网络的。环境刺激是从该环境的不同状态获得的输入—输出数据值。在训练过程中，系统地更新自由参数，使其值收敛到最优值。自由参数更新的大小由一个称为学习率的因素控制。何时停止训练取决于预先定义的条件，如达到最大期望的训练时间和最低错误率等。

3.3.2 神经网络逆解

神经网络类似于人脑学习的过程，神经网络参数的准确性和学习数据量的多少有很大的关系。输入为并联机器人关节的角度值经过神经网络模块输出为机器人的末端的位置和姿态，如图3 所示。运动学简化模型示意图可以得到：

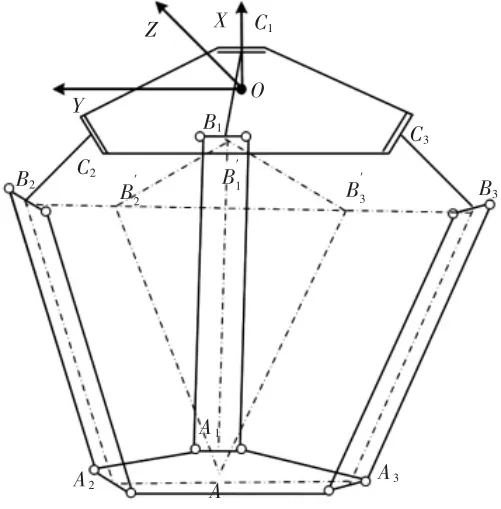
图3 运动学简化模型Fig.3 Simplified Kinematics Model

整理公式可以得到：

根据上面所述的非线性方程组，采用三层BP 神经网络方法对并联机器人运动学进行正向求解。根据并联机器人的外观结构构型，建立基于神经网络的并联机器人非线性方程。神经网络拓扑结构共分为三层，输入层共有3 个神经元，输出层有4 个神经元，如图4 所示。可经由下式将机器人正运动学的非线性映射转换为线性映射，设N个样本为（Pj，αj），其中j＝1，2，…，N。Pj为网络输入向量，作为第j个位置样本，αj作为第j个电机转角为网络输出向量。

式中：wi—隐含层的节点i与输入层的权值；a1i—隐含层的节点i与输入层的阈值；wk—输出层与隐含层间的权值；a2k—输出层与隐含层间的阈值。

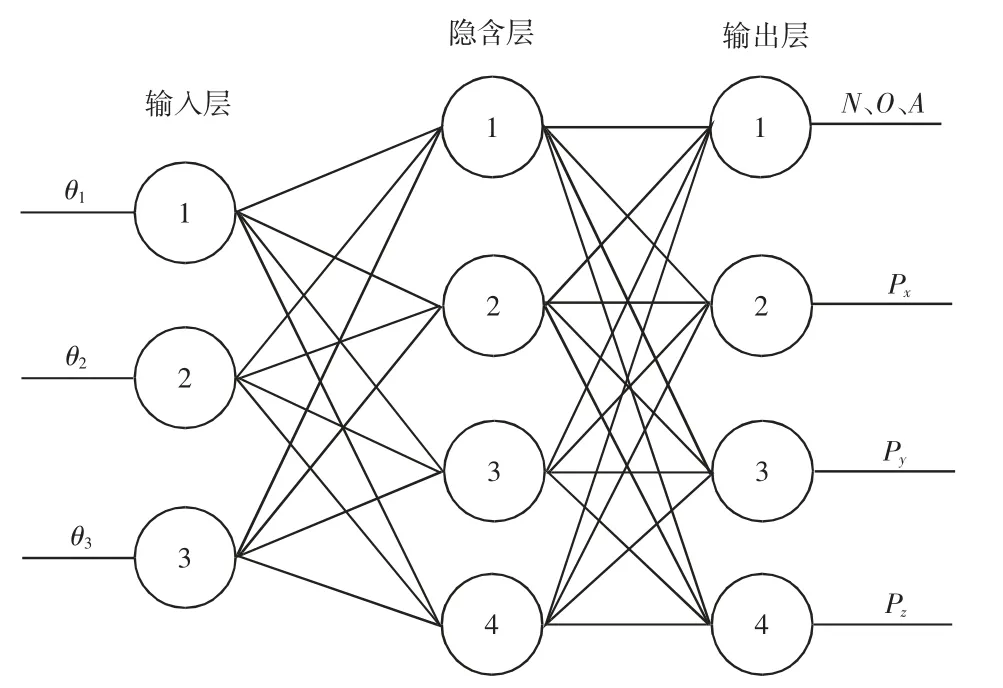
图4 三层前向神经网络结构Fig.4 Three-Layer Feedforward Neural Network Structure

将并联机器人运动控制过程中产生的位置和关节角度进行保存，作为大量样本输入训练后，可以获得机器人关节角度到机器人末端位置的运动学正描述，即可根据建立的非线性方程和权重从而得到并联机器人正解。

4 NURBS 的轨迹规划

在数控控制器的轨迹规划中，最大加速度和最大颠簸的控制是非常重要的，因为它在很大程度上影响着机器人运动稳定性。线性插补器和圆形插补器的典型问题包括：处理大量短节段需要过多的数据传输和加工时间。线段连接处的速度不连续明显，传统的方法已不能满足当前制造业对高速高精度加工的要求。

4.1 样条曲线类型概述

在变进给量控制中，NURBS 曲线上每个采样点的进给量是根据该点的曲率和允许的弦误差确定的。然后在泰勒展开中使用这个进给量来确定下一个采样点。众所周知，进给速度必须根据轨迹的曲率变化而变化，在高速加工中应尽可能快地保持进给速度。同样，当一个弯曲区域之后是一个平坦区域时，也有必要确定速度开始增加的点。

在加工过程中，通过刀具路径规划将参数曲面离散成一组参数曲线，然后执行轨迹规划对每条曲线进行插值。参数曲线有不同的表示形式，NURBS 曲线由于其计算速度快、计算稳定性好，已被许多CAD/CAM 系统用作基本几何表示。提出了一种NURBS 曲线插补的综合插补方案。以NURBS 曲线为例，对所开发的轨迹规划进行了逐步测试。该曲线由直线段和任意曲线段在锐角处连接而成。传统的机器人运动规划只提供线性和圆形插补器，使用线性化的线段序列来逼近曲线。这种传统的方法由于分割导致进给量波动较大，并产生较大的数据文件。对于一般参数曲面运动控制，该方法效率低，易产生误差。

4.2 NURBS 样条曲线规划步骤

由于这种运动规划是实时实现的，因此开发了特定的算法来计算每个采样间隔的进给量和采样点。NURBS 样条曲线拟合过程如下：

（1）节点参数ui计算过程（累计弦长法）

到此，B样条曲线就拟合出来了。接下来需要对曲线进行数据点的密化，好让机器人周期性走到各个密化点，一般采取泰勒展开的方式密化。

5 实验

5.1 运动控制实验

为了实现机械手的实时轨迹控制，讨论的正，逆运动学一般必须在线计算。验证了并联机器人正运动学的正确性，如图5（a）～图5（b）所示。在机械臂的运动学分析中，将给定的执行机构坐标转换为直角坐标的正逆运动学都是必要的，该策略在不到两次迭代和0.02 s 的执行时间内，位置和方向参数的精度分别接近0.01mm 和0.01°。

图5 正弦与圆弧跟踪曲线示意图Fig.5 Sine and Arc Tracking Curve Diagram

5.2 NURBS 样条曲线实验

NURBS 插补器在插补过程中既能在大部分时间内实现均匀进给，又能在每一个插补点都能在规定的误差范围内。曲线的尖角或进给敏感角，避免高频分量或含有与插补轨迹中机器固有频率匹配的频率分量和高抖动，如图6 所示。在轨迹规划方法中，提出了一种检测NURBS 曲线尖角的前瞻模块。在此基础上，采用加减速方法进行了修正，满足机器人的加减速能力。

图6 NURBS 样条曲线示意图Fig.6 NURBS Spline Diagram

5.3 实际抓取运动实验

为了实际验证并联机器人运动控制正确性，为并联机器人运动抓取实验，如图7（a）～图7（b）所示。依靠千分表可以进行测试，得并联机器人重复定位精度（±0.05）mm，运动速度快，拾放节拍120 次/min。并联机器人为生产线系统提供了稳定运动控制功能，并联机器人准确识别并同步跟踪传输线上高速运动的产品，在高速运动中连续抓取多包产品，然后整齐的摆放到包装箱中。

图7 运动抓取示意图Fig.7 Motion Grab Diagram

6 结论

针对并联机器人运动控制与NURBS 轨迹规划问题，提出了神经网络正运动学控制与NURBS 轨迹规划控制方法。并联机器人FKP 的求解是闭环控制系统的关键，由于缺乏一种封闭形式的数学解，提出了神经网络解决运动学正解通用逼近器。在该模型中，输入端接收信号将其传输到神经元处理单元，在神经元处理单元中，信号通过权值乘法进行修改。然后提出了一种NURBS曲线插补的综合插补方案，同时满足给定速度和弦长精度的要求。用NURBS 样条拟合方法对插补后的进给曲线进行进一步平滑，在插补过程中，反复检查弦长误差，并将其限制在规定的误差范围内。从正运动学仿真、逆运动学和NURBS 样条曲线验证了软件有效性。这种混合策略确实需要稍微增加计算机系统内存，但是节省的时间和迭代次数的节省足以克服引入神经网络的成本。并联机器人运动学策略在不到两次迭代和0.02s 的执行时间内，位置和方向参数的精度分别接近0.01mm 和0.01°。在实际抓取运动过程中，并联机器人重复定位精度±0.05mm，运动速度快，拾放节拍120 次/min，验证了算法的有效性和正确性。