全方位装配机器人的刚度误差分析

叶长龙，万缯齐，于苏洋，姜春英

（沈阳航空航天大学机电工程学院，辽宁 沈阳 110136）

1 引言

机器人以其多功能性以及良好的适应性被广泛应用于生产实践中。而并联机器人相对于串联机器人又具有高刚度，高精度，高承载力以及累计误差相对较小等的优点，近年来被广泛的研究与应用。精度是衡量机器人性能的重要指标，精度的提高将使机器人的应用范围更加广泛。为了提高机器人的精度，国内外研究人员进行了一定的分析与研究。例如应用于食品包装工业的Delta 机器人[1]，通过改进机构使得其精度大大提高，改进后可对易碎品进行操作。文献[2]通过改变机器人的DH 模型使其精度得以提高。文献[3]通过关节反馈补偿的方法提高了机器人的精度。

刚度是评价机器人机构抵抗变形能力的重要指标。通过对机器人进行刚度分析来提高机器人精度同样是一种提高机器人精度的方法。文献[4]通过位置逆解法对Bicept 机器人进行了刚度分析。文献[5]通过矢量叠加法提高了机器人的刚度。

针对目前的研究现状，结合减小变形误差的分析目的，对所研究机器人机构进行了刚度建模。结合旋量理论进行了刚度分析并通过实验得出了变形误差最大的产生位置，对误差的减小提出了改进方案。

2 机器人结构分析

实验室自主研制的全方位机器人的结构图，如图1 所示。该机器人主要由上平台，驱动支链，限位支链以及全方位下平台组成。下平台由四组全方位轮支撑，可以实现机器人的全方位移动。这里的分析对象主要为举升机构，如图2 所示。其中，上下两平台间由四条支链组成，其中两条驱动支链由丝杠组成，丝杠可在电机的驱动下进行伸缩。两条限位支链由直线伸缩导轨组成。通过丝杠的伸缩改变驱动支链的长度，可以实现上平台的翻转[6]。

图1 全方位机器人的三维模型Fig.1 3D Model of Omni-Directional Robot

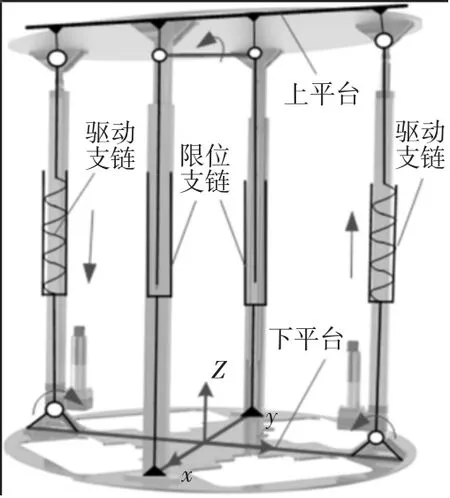
图2 举升机构结构图Fig.2 Lifting Mechanism Structure

采用修正的G-K公式的一般的通用公式进行自由度计算[7]：

式中：M—机构的自由度数；n—包含机架在内的构件数目；g—运动副数目；fi—第i个运动副的自由度数；μ—机构中存在的全部过约束数目。

代入数据得M=6×（10-10-1）+8+0=2。

求得机构自由度为2。加以分析可得在驱动支链上伺服电机带动丝杠运动的条件下，可以实现平台的绕x轴翻转以及沿z轴升降两个自由度的变化。机器人的结构性能参数，如表1 所示。

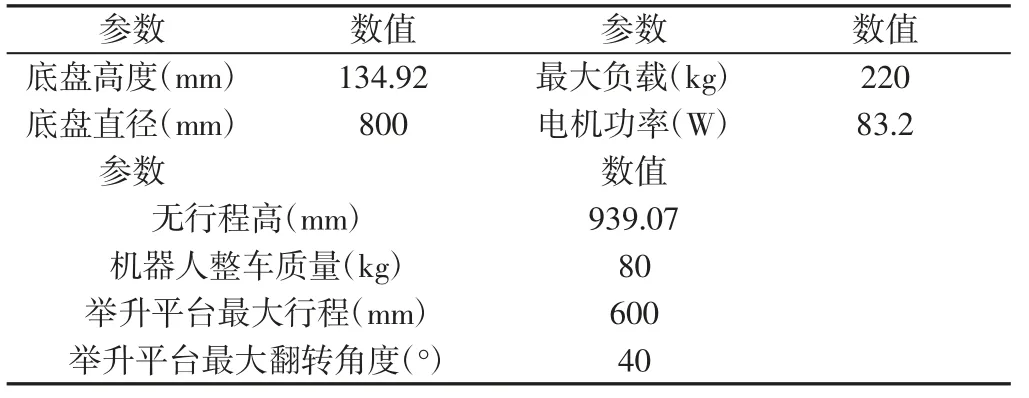
表1 机器人的结构性能参数Tab.1 Structural Performance Parameters of the Robot

3 机器人静刚度分析

3.1 机器人刚度模型的建立

当全方位机器人进行运动时，末端执行器会对周围环境施加一定的力旋量。该力旋量源于驱动器，即电机，通过丝杠传递到上平台。反之，这种力旋量也可能会使上平台偏离理想位置，从而衍生出机器人一项重要的性能指标，即静刚度。

机器人的静刚度与多种因素有关：如各组成单元的材料及其几何特性、传动机构类型、驱动器、控制器等。每一因素对于机器人的静刚度都有不同的影响。对于研究的机器人机构中有四根细长杆，这势必会影响机构的整体刚度，机器人的刚度性能会直接影响机器人的定位精度。为提高机器人的定位精度，对机器人进行刚度分析是必要的。

这里的研究对象的静刚度映射是指驱动电机与传动丝杠的输入刚度与并联机构动平台的输出刚度之间的映射关系，驱动电机以及丝杠的传动部分是研究对象仅有的柔性元。对于组成机器人的各杆件以及其他部件，柔性极小[8]，可忽略不计。刚度分析的具体过程如下：

基于旋量理论，对机构加以分析后得出并联机器人的旋量分布，如图3 所示。

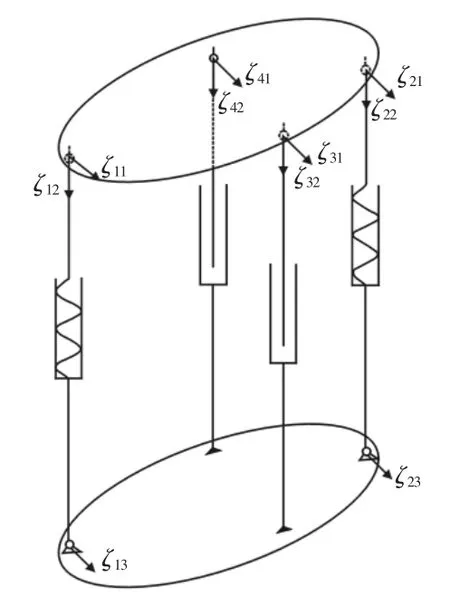
图3 旋量分析Fig.3 Screw Analysis

式中：c1的大小—支链1 与上平台铰接处转动副旋转中心与上平台圆心沿平台方向的直线距离的数值；d1的大小—支链1的长度大小；s11与s13—各自所在转动副转动的角速度；s12—支链1 与上平台铰接处沿支链1 轴线方向的线速度；ζ11与ζ13的方向—沿各自转动副的轴线方向；ζ12的方向—沿支链1 的轴线方向。

根据螺旋理论，分析后可知支链1 具有一个约束反螺旋[9]：

3.2 各支链受力求解

并联机构的受力分析，如图4 所示。

图4 受力分析Fig.4 Force Analysis

直线伸缩导轨的内外两条导轨之间的摩擦非常小，再加上导轨的放置方式为竖直放置，这种条件下的摩擦力更是几乎为零。所以直线伸缩导轨不会受到来自上平台以及载荷的竖直向下的压力。

机构的刚度与机构所受到的力以及在力作用下所产生的变形有关，而机构受力所产生的变形大小与机构本身的形态以及制造机构所用材料的弹性模量有关。为了求得所需参数，现对并联机器人各部件长度加以分析。

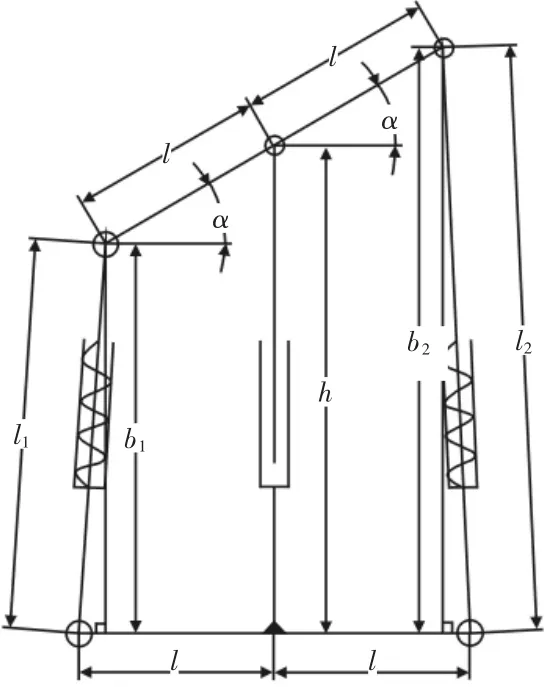
图5 长度标定分析Fig.5 Length Calibration Analysis

在不影响将推得结论的正确性以及不会产生误差的情况下，将机构简化，如图5 所示。构造两辅助线b1，b2，则有：

两条支链的变形均可各分为两部分，即沿丝杠方向的压缩变形以及垂直于丝杠方向的弯曲变形。

则由几何关系可得两丝杠长度变量如下：

上平台变形主要为垂直于平台方向的挠曲变形，垂直于平台方向受力为Gcosα，即：

3.3 理论等效弹簧常数求解

下面对各支链的等效弹簧常数求解如下：

首先1，2 支链的等效弹簧常数求解方式相同，系数如下：

式中：E4—支链4 材料的弹性模量；I4—直线伸缩导轨截面的惯性矩；h—上平台圆心与下平台圆心之间的直线距离。

4 仿真分析

将机构的基本参数代入之前建立的刚度模型，并对各个支链加以分别分析，得出的仿真结果，如图6～图8 所示[12]。

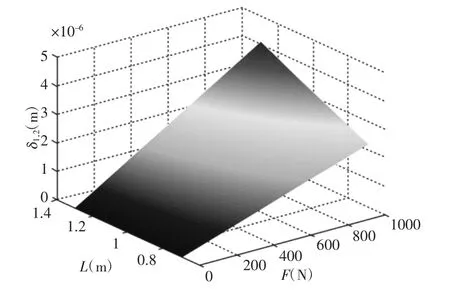
图6 支链1，2 仿真结果Fig.6 Simulation Results of Branch 1，2

图7 支链3 仿真结果Fig.7 Simulation Result of Branch 3

图8 支链4 仿真结果Fig.8 Simulation Result of Branch 4

从图6 的仿真结果可以看出，支链长度与载荷大小与支链1，2 变形量大小均成正比关系，变形量的量级很小，为10-6m。

从图7 的仿真结果可以看出，载荷大小与支链3 变形量大小成正比关系。变形量的量级较大，为10-3m。

从图8 的仿真结果可以看出，上平台圆心到下平台的垂直距离以及载荷与支链4 的变形量大小成正比关系。变形量的量级同样较大，为10-4m。

5 实验分析

对全方位机器人的刚度性能进行实验分析。实验用的全方位机器人，如图9 所示。实验内容主要是通过刚度标定传感器对机器人的变形量进行测定，然后对所得变形量与仿真所得的理论变形量进行比对，从而得到理论值与实测值的偏差大小。

图9 实验用机器人Fig.9 Experimental Robot

图10 实验1Fig.10 Experiment 1

仿真分析的条件为理想条件，实际机构中存在许多未被考虑到的误差因素将影响机器人各支链的刚度，如支链横截面积的变化以及铰链处的装配间隙造成的误差。故通过实验测量并计算出实际的刚度值并与理论值进行比较，使分析内容实体化。

实验过程中的负载是通过在实验盒内添加不同质量的法码来实现。

对支链1，2，3 进行了实验1，如图10 所示。实验中支链1，2受力相同，均为盒内添加载荷所受重力与上平台自重的重力的和的一半。支链3 受力为盒内添加载荷所受重力。通过改变盒内载荷质量进行了多组实验。实验数据，如表2～表4 所示。

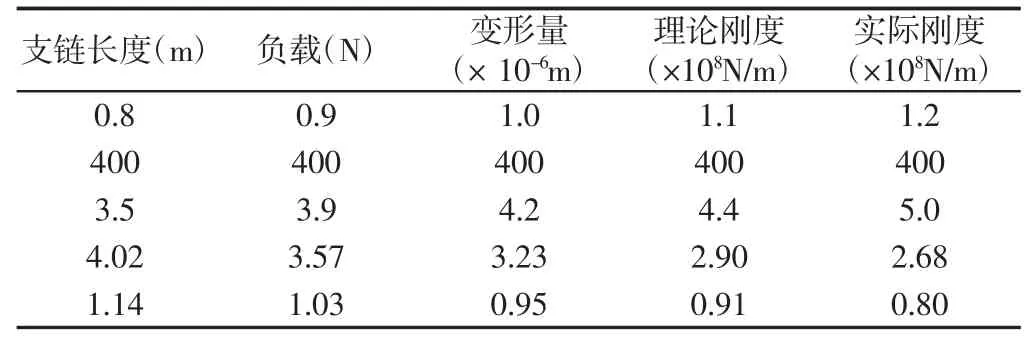
表2 支链1 实验数据Tab.2 Branch 1 Experiment Data

表3 支链2 实验数据Tab.3 Branch 2 Experiment Data

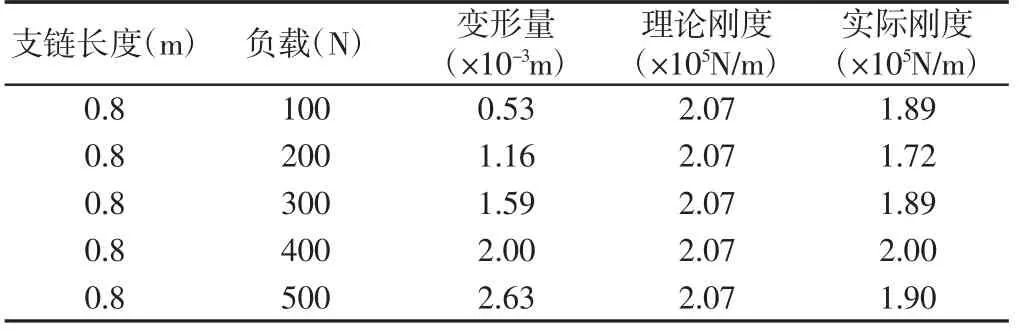
表4 支链3 实验1 数据Tab.4 Branch 3 Experiment 1 Data

从表2，表3 的实验数据来看，实际刚度与理论刚度的变化趋势是相同的，即随着丝杠的伸长刚度随之减小。但实际刚度的值相对于理论刚度的值较小，这是由于支链实际的横截面积相对于理论横截面积偏小所致。

图11 支链3 实验2Fig.11 Branch 3 Experiment 2

从表4 的实验数据来看，实际刚度与理论刚度相差无几。这主要是因为此组实验的误差产生因素较少，可能的误差产生因素只有两驱动支链的装配间隙差引起的刚度误差，故此组实验理论值与实际值偏差较小。当载荷被施加在距上平台边缘5cm 时进行了另一组实验，如图11 所示。

实验结果，如表5 所示。

表5 支链3 实验2 数据Tab.5 Branch 3 Experiment 2 Data

从表5 的实验数据来看，实际刚度与理论刚度偏差很大。这说明这一部分的装配误差很大。从结构来看，引起此误差的因素为驱动支链上下铰链的装配误差以及丝杠弯曲所造成的误差。

最后对支链4 进行实验分析，实验方法为翻转上平台并在其上施加载荷，测量支链的弯曲变形，如图12 所示。实验结果，如表6 所示。

图12 支链4 实验Fig.12 Branch 4 Experiment

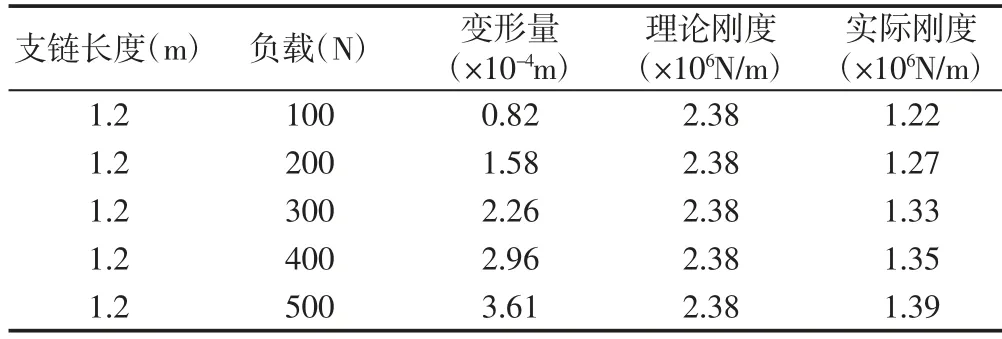
表6 支链4 实验数据Tab.6 Branch 4 Experiment Data

此组实验误差同样较大，造成的原因为铰链处装配精度误差。对各支链的误差进行整合比对，如表7 所示。

表7 各支链变形误差量级Tab.7 Deformation Error Magnitude of Each Branch

显然，支链3 边缘的变形误差最大。为了提高机器人精度，减小变形误差对机器人精度的影响，首先就要针对这一变形误差加以改进。改进的方法可以通过在上平台上加装加强筋来提高这一部分的刚度。

6 结论

（1）运用旋量理论对全方位并联机器人进行旋量分析，建立旋量与刚度之间的联系，运用旋量理论求解了机器人的刚度矩阵。（2）对全方位机器人进行受力分析，建立了传统力学模型下的变形模型。并对机器人进行了特定工况下的刚度仿真，求解了并联机器人的理论刚度。（3）对全方位机器人进行了实验分析，并分析了理论值与实测值产生偏差的原因，进而针对原因提出改进思路，提高机器人精度。