小学数学教材中“认识三角形和四边形”的内容编排分析与比较——以“人教版”“苏教版”“北师版”为例

徐文彬，彭 亮，任利平，谢春艳，王国红，资安琪，林敏婷，刘艳杰，薛 悦

小学数学教材中“认识三角形和四边形”的内容编排分析与比较——以“人教版”“苏教版”“北师版”为例

徐文彬1，彭 亮2，任利平1，谢春艳1，王国红1，资安琪1，林敏婷1，刘艳杰1，薛 悦1

（1．南京师范大学 课程与教学研究所，江苏 南京 210097；2．南京晓庄学院，江苏 南京 211171）

“认识三角形和四边形”是小学数学学习中十分重要的内容．据此，从纵向和横向两个维度对人教版、苏教版和北师版小学数学教材中相应内容进行了分析与比较．通过纵向分析与比较发现，3个版本教材的相同点是直角三角形、长方形以及正方形呈现数量最多，集中分布在四、五年级，且在四边形中，菱形、鸢形、一般梯形和一般四边形出现较少，不同点是不同的三角形和四边形在不同年级的分布不同．通过横向分析与比较发现，3个版本教材在例题内容组织上存在较大差异；在例题的情境创设上，人教版和苏教版情境类型较为一致，而北师版的真实情境相对较少；例题的学习进程大致相同；例题的思维水平主要集中在视觉和分析水平上；习题的内容组织较为相同；习题的问题形式主要是以视觉形式或视觉形式组合其它形式表示为主；习题的问题结构主要以封闭问题和半开放问题为主；习题的思维水平主要集中在视觉、分析和非形式化演绎水平上．因此，教材的编写，需整体把握图形认识的5个维度，兼顾直观认识与数学内容的本质探寻，以及注重学生几何直观与逻辑推理能力的培养．

小学数学教材；人教版；苏教版；北师版；认识三角形和四边形；内容编排分析与比较

1 问题提出

国内对“认识三角形和四边形”已展开了一些研究，但多数研究都是基于教学实践思考而提出相关教学建议，注重经验迁移、重视直观操作、变式教学中掌握图形本质属性等是其主要提及的教学策略[1-3]．有的研究则关注图形概念，依据概念教学的基本过程，在引入、理解和运用3个环节提出相应的探究学习方式[4-5]，但在概念理解中进一步提及要在图形大背景下，以静态比较或动态改变的方式认识图形概念联系的研究仍比较少[6-7]．此外，有些研究是在教材审视中理解教学目标，提出实施策略，其中以教学内容的分析为主[8-9]，“图形认识”背景中理解该内容的较少[10]．从已有研究可见，展开教材分析的结构化研究虽少，但都关注到教材内容对教学实践的指导意义．因此，选择在合理的教材内容编排分析框架构建下，结合“图形的认识”知识背景，以分析“认识三角形和四边形”主题，以期能从教材内容组织编排中理解编写意图，并为教材内容的完善提供些许改进建议，为教师合理利用教材开展教学实践提供思考方向．

2 研究设计

研究对象是人民教育出版社的小学数学教材（2012年、2013年审定，简称“人教版”），北京师范大学出版社的小学数学教材（2013年审定，简称“北师版”），以及江苏教育出版社的小学数学教材（2013年审定，简称“苏教版”）．

2.1 研究问题

通过对人教版、苏教版和北师版教材中“认识三角形和四边形”的内容结构与编排进行分析，审视3个版本教材在内容呈现、整体结构、编排特点，以及可能对教学产生的影响等方面的异同．具体而言，主要包含以下3个问题：（1）3个版本教材内容在12册教材中的呈现及与前后知识的联系；（2）3个版本教材内容的结构与编排特点；（3）3个版本教材内容编排及其特点对教学实践可能产生的影响．

2.2 分析框架

通过前期文献阅读与梳理，在已有研究基础上，结合“认识三角形和四边形”的具体内容，确立了小学数学教材中该内容的编排分析框架（参见表1）．

整体而言，内容编排分析框架从纵向和横向两个维度、量和质两个方面来对教材内容编排进行全面分析．其中，纵向维度重在考查“认识三角形和四边形”内容在不同年级教材中的前后关联，横向维度重在考查其具体内容的编排；量的分析从数量的角度来考查例题和习题的整体情况，质的分析从内容的角度来考查例题和习题的具体情况．

纵向维度中的量的分析是考查不同种类的三角形和四边形在12册教材“图形与几何”领域直观呈现的数量；纵向维度中的质的分析是考查“图形的认识”内容（包含“三角形和四边形的认识”）在12册教材例习题中的内容旨向及对应的知识点．

横向维度中的量的分析是考查“认识三角形和四边形”中设置的例题与练习数量；横向维度中的质的分析包含例题和习题两个方面．

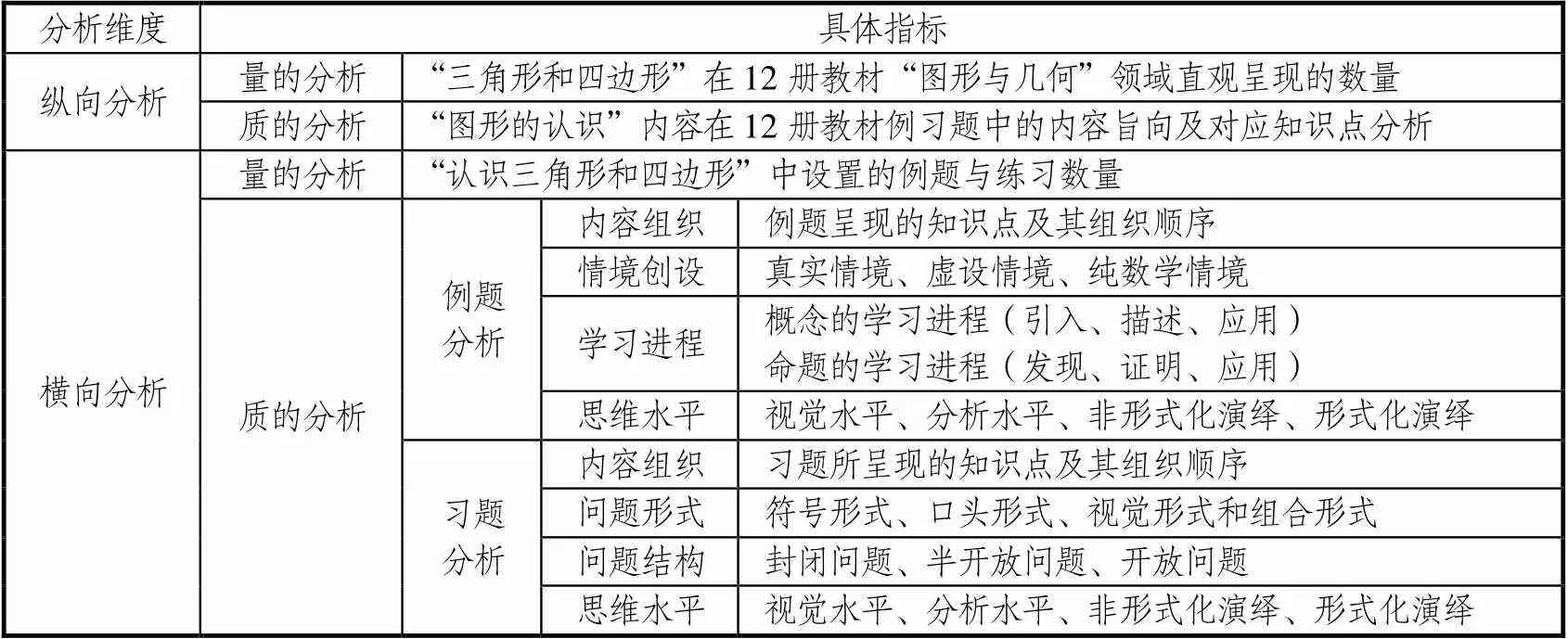
表1 小学数学教材中“认识三角形和四边形”的内容编排分析框架

例题涉及内容组织、情境创设、学习进程、思维水平4个方面．例题的内容组织是考查例题呈现的知识点及其组织顺序．例题的情境创设依据华东师范大学徐斌艳的研究成果[11]，将情境分为3种类型：（1）真实情境，指来自日常生活、外部现实世界（自然、艺术、体育、人文等），或文学作品、科幻作品等的故事情节，这种情境是真实的、非人为构造的，如几何实物图、几何数学史、学生生活空间；（2）虚设情境，指有一定现实依据的、人为构造的情境，这种情境是非真实的，其情节、数据都是为开展教学人为构造的；（3）纯数学情境，指纯粹数学问题表述，如纯粹呈现数学抽象的符号、图形的情境．例题的学习进程包括概念的学习进程和命题的学习进程两个方面，依据宋运明的研究成果[12–13]，将概念的呈现分为引入、描述和应用3个过程，将命题的呈现分为发现、证明和应用3个过程．例题的思维水平依据范希尔理论几何思维水平的划分，从视觉水平、分析水平、非形式化演绎、形式化演绎4个方面进行分析．

习题涉及内容组织、问题形式、问题结构、思维水平4个方面．习题的内容组织是考查习题所呈现的知识点及其组织顺序．习题的问题形式依据王子玲、杨德清[14]的研究，从符号形式、口头形式、视觉形式以及组合形式进行分析．其中，符号形式是指一个数学问题中只包含数学表达式，也就是用数学语言来表达的；口头形式是指一个问题仅以口头形式提出，也就是说是用生活化的语言而不是数学术语来表达的；视觉形式是指一个问题以图形、图片、图表、表格等形式来呈现，所有的条件都包含在图中；组合形式是指在同一个问题中，采用两种或两种以上形式表示．习题的问题结构依据李鹏[15]和戴再平[16]的研究，从封闭问题、半开放问题、开放问题进行分析．其中，将条件和结论是否确定、策略是否唯一作为判断问题结构的依据．封闭问题是指条件、结论和策略3者均不开放，半封闭问题是指其中的部分要素开放，开放问题是指3个要素均开放．习题的思维水平依据范希尔理论几何思维水平的划分，从视觉水平、分析水平、非形式化演绎、形式化演绎4个方面进行分析．

3 研究结果与分析

3.1 纵向分析结果

纵向分析主要是分析教材中所出现的与“认识三角形和四边形”单元前后相关的内容，包括量的分析与质的分析两个方面，具体结果如下．

3.1.1 量的分析

小学数学3个版本的教材中，“认识三角形和四边形”都以不同的方式蕴含在不同年级中．量的分析主要对教材中出现的三角形和四边形进行分类统计，分别考察不同的三角形和四边形在6个年级的教材中直观呈现的现状，以期发现三角形和四边形在不同年级的“潜伏”与拓展（可分别参见图1、2、3，图4、5、6）．

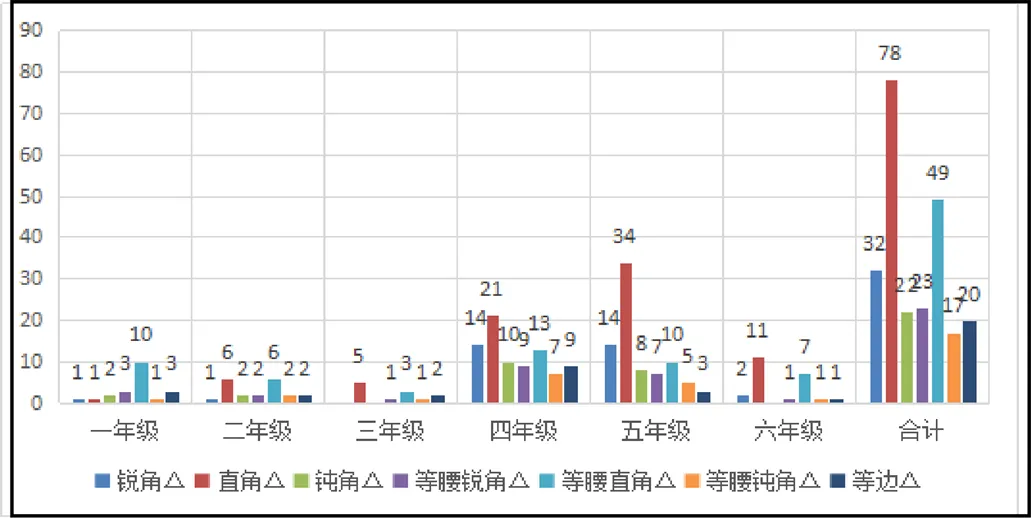
图1 人教版小学“图形与几何”领域中“三角形”直观 呈现的数量分布

图2 北师版小学“图形与几何”领域中“三角形”直观 呈现的数量分布

图3 苏教版小学“图形与几何”领域中“三角形”直观 呈现的数量分布

由图1、2、3可知，3个版本的教材存在下述异同点．就相同点而言，其一，在“三角形”直观呈现中，以直角三角形的图形呈现数量最多；其二，从不同年级的数量分布来看，在“三角形”直观呈现中，以四、五年级的数量居多．

就不同点而言，每一种三角形在不同年级的分布不同．在人教版中，锐角三角形和直角三角形在四、五年级直观呈现的数量较多，钝角三角形、等腰锐角三角形和等腰钝角三角形主要出现在四、五年级，等腰直角三角形在6个年级的数量分布差距不大，等边三角形主要分布在四年级；在北师版中，锐角、钝角、等腰锐角、等腰钝角三角形主要分布在四、五年级，直角和等边三角形主要分布在四、五、六年级，等腰直角三角形分布较为均匀；在苏教版中，锐角三角形主要分布在四、五年级，直角三角形、钝角三角形、等腰锐角三角形、等腰直角三角形和等腰钝角三角形主要分布在四年级，等边三角形在各个年级分布较少．

图4 人教版小学“图形与几何”领域中“四边形”直观 呈现的数量分布

图5 北师版小学“图形与几何”领域中“四边形”直观 呈现的数量分布

图6 苏教版小学“图形与几何”领域中“四边形”直观呈现的数量分布

由图4、5、6可知，3个版本的教材存在下述异同点．就相同点而言，其一，在“四边形”直观呈现中，对不同图形的侧重有较大差异，对长方形和正方形的感知往往成为小学阶段的重点；其二，在“四边形”直观呈现中，以四、五年级的数量居多，一、二、三、六年级的数量较少；其三，菱形、鸢形、一般梯形和一般四边形出现较少．

就不同点而言，平行四边形、等腰梯形和直角梯形在不同年级的分布不同．在人教版中，平行四边形、等腰梯形和直角梯形主要出现在四、五年级；在北师版中，平行四边形主要出现在四、五年级，等腰梯形和直角梯形主要分布在五年级；在苏教版中，平行四边形主要出现在二、四、五年级，等腰梯形和直角梯形主要分布在四、五年级．

3.1.2 质的分析

图形的认识基于图形的点、线、面、体等基本特征．因此，在12册教材中，对此进行质的分析，可以纵向地把握教材编写的逻辑，并从图形认识的整体出发，发现图形之间的内在联系．通过对3个版本教材中点、线、面、体等的分析，可以得到如下一些结果．

就图形认识的内容分布而言，虽然3个版本教材“图形与几何”相对集中分布在四、五年级，但是在每一年级、每一册教材中基本都有涉及对图形的认识．

就图形认识的概念关系而言，在3个版本的教材中，第一学段认识图形的过程是“三维、二维——二维（角）、一维——二维”，第二学段认识图形的过程是在对线的了解、对线与线之间关系的认识的基础上，交替学习平面图形与立体图形．由此，学生在第一学段时已整体把握了图形的外部特征，基本能够在看到图形时说出图形的名称，因此，“认识三角形和四边形”作为二维图形的再认识内容，其要求是进一步从图形的各部分结构及名称、关系来描述图形的特征，既是从点、线、角对图形进行分解的认识，也是从高和底构成对图形“面”的感知．

就图形认识的内容指向而言，主要涉及直观认识概念、图形的构成要素、图形与图形之间的关系以及图形的定义等4个方面．其中，直观认识概念在例题中主要表现为呈现某一图形并有相应的图形名称以标识，在习题中主要表现为从实物或图形模型中识别图形，或者要求学生画出什么图形，以使图形的直观形象与名称相匹配；图形的构成要素只要在例题中直观呈现也会对面、边、顶点、高或底进行标识；图形与图形之间的关系主要是在平面图形中，较多出现的是对图形进行剪切、拼接、折叠、重合等操作；图形的定义，分析教材中所给的图形定义可发现，小学阶段已有的定义方式包括两种，一种是从图形特征、性质出发定义图形，比如线段、射线、直线，平行线和垂线，平行四边形、梯形和三角形，以及长方体和正方体等；一种是从操作过程出发定义图形，比如角（平角、周角）、高和底．

3.2 横向分析结果

横向分析是关于“平行四边形和梯形”以及“三角形”内容的例习题的分析．

3.2.1 例题分析

例题分析主要包括内容组织、情境创设、学习进程和思维水平4个方面．

（1）内容组织．

由表2可知，3个版本在这一内容的编排上有很大的区别．这种区别不是所学内容的差异，而是在于“如何帮助学生构建这一内容体系”方面存在不同．

表2 3个版本小学数学教材中“认识三角形和四边形” 内容的例题之内容组织

就人教版而言，在四年级上册，首先安排了4道例题以展开“平行与垂直”内容的教学，再来认识平行四边形和梯形；而“三角形”作为一个单元的教学内容，安排在四年级下册．教材选择先认识“平行四边形和梯形”，再认识“三角形”，一是与“平行与垂直”的联系比较直接，二是此顺序与之后学习“多边形的面积”的线索基本一致，如何求出梯形、三角形面积都是以分割平行四边形为基础．

就苏教版而言，一是注重已学知识对新知识的奠基和支点作用，譬如，平行四边形和梯形高的学习就以三角形的高的作法为基础；二是三角形、平行四边形和梯形的学习完全独立开来，且三角形的学习较之平行四边形和梯形的学习较为充分．

就北师版而言，一是教材注重学生先前知识经验与后续学习之间的关系，采用类比、迁移的设计思路，譬如，从“图形分类”到“三角形分类”再到“四边形分类”较好地体现了这一点；二是教材采用下位学习的结构，先学习图形分类，让学生在图形分类中整体上初步认识三角形和四边形，接下来是三角形和四边形的具体内容学习；三是教材将重点放在三角形的认识和学习之上．

（2）情境创设．

对“认识三角形和四边形”内容的例题情境类型进行分析，其结果如表3所示．

表3 3个版本小学数学教材中“认识三角形和四边形” 内容的例题之情境类型

由表3可知，人教版和苏教版在“认识三角形和四边形”的情境类型上较为一致，而北师版的真实情境相对较少．

真实情境能够帮助学生在图形的形象感知基础上学习抽象的图形，这是图形认识一般的路径，譬如，在人教版教材中，由扶梯、挂衣架、瓷砖等抽象出了平行四边形，由梯子、堤坝、鞍马等抽象出了梯形，由金字塔、大桥吊索、红领巾、交通标识等抽象出了一般的三角形及特殊三角形．

纯数学情境需要学生通过视觉观察、绘图操作、语言描述以发现图形的特征，在这一过程中，学生是从图形的构成要素出发以获得对图形特征的抽象分析．因而，纯数学情境对学生思维水平要求很高，同时也有利于学生几何思维水平的提升．譬如，北师版教材中的“图形分类”．

虚设情境主要通过人为虚构的情境来帮助学生学习图形的特征，因而，虚设情境可能与现实不太相符，但却有利于学生发现情境中所蕴含的数学知识．譬如，苏教版教材中测量人字梁的高度和探究三角形三边关系所用到的小棒都可视作这一情境类型．

（3）学习进程．

小学阶段“认识三角形和四边形”既有概念的学习，也有命题的认识，因而将学生的学习进程分为两个方面：一是概念的学习进程，二是命题的学习进程．

就3个版本例题中概念学习进程而言，概念的学习并不总是经历完整的“引入—描述—应用”的学习进程，概念的认识也并非总是需要经历完整的学习进程．一般对于新概念的学习，学生需要在概念的引入、描述、应用中逐渐加深对概念的理解，但对于已有概念，一般只需要经历概念的应用阶段，从而过渡到新概念的学习．比如，北师版教材在“平行四边形和梯形”的概念学习中，就是通过“四边形分类”来引入，用“文字”来描述，以“图形识别”为应用的．

就3个版本例题中命题学习进程而言，学生主要需要经历命题发现的进程．命题的发现是一般命题学习的主要方式，这一过程中主要体现的是学生的归纳概括能力，学生需要从大量实例出发，观察比较以得出发现，进而继续选取实例以验证猜想、解释说明．这与小学生的认知水平基本吻合．比如，人教版教材在“平行四边形具有不稳定性”这一命题的学习中，就是通过大量生活实例和动手操作来发现，并以更多实例来验证“发现”和解释说明的．

（4）思维水平．

对例题思维水平进行分析，主要目的是考察教学内容在思维层次上对学生的要求．这里采用范希尔理论几何思维五水平划分法，考虑小学生几何思维水平和教材内容尚未达到第五水平，故仅对前4个水平进行分析（可参见表4）．

表4 3个版本教材中“认识三角形和四边形”内容的 例题之思维水平

由表4可知，3个版本的例题思维水平主要集中在视觉水平和分析水平上．这与小学生的认知水平较为符合．

此外，例题在不同思维水平的设置上体现了一定的基础性和层次性，譬如，在北师版例题1所涉及的图形的分类和三角形的稳定性中，对学生提出视觉水平和分析水平上的要求．与此同时，在视觉水平和分析水平的基础上，教材也对学生思维上非形式化演绎水平和形式化演绎水平的提升提出了要求，譬如，人教版中例4有关四边形之间关系的分析即对非形式化和形式化演绎化水平有一定的要求．

3.2.2 习题分析

习题分析主要包括内容组织、问题形式、问题结构、思维水平4个方面．

（1）内容组织．

对“认识三角形和四边形”主题的习题进行内容组织上的分析旨在发现习题的编排理念及其对学生的要求（参见表5）．

由表5可知，就相同点而言，一方面从习题所反映的知识点来看，“关于三角形的认识”相关习题较多，“关于四边形的认识”相关习题较少．另一方面，反映同一知识点的习题之间具有一定的层次性，体现出不同的难度梯度．从一般的对图形的基本认识、判断、辨识到动手实践操作（包括摆一摆、画一画、折一折、剪一剪等活动），体现出习题的层次从认识与理解知识到运用知识的过程，习题的难度不断加大，同时对学生的要求也逐渐提高．

表5 3个版本教材中“认识三角形和四边形”内容的习题之内容组织

就不同点而言，在图形之间关系的整体认识上，各版本教材习题的设计不太一样．其中，人教版和苏教版教材未能涉及到四边形图形之间关系和特征的本质理解．无论是在三角形的习题还是在四边形的习题中，其要求主要针对的是图形的基本特征和要素，甚少关注图形之间的关系，仅有的图形分类也主要关涉图形的特征，而对它们之间的演变关系甚少涉及．而北师版教材则较为注重学生对图形整体间的逻辑关系的理解，尤其是图形关系的理解类型的题目占据一定的比重，其通过剪切、拼接等手段让学生感受到三角形、四边形之间的分解与组成关系．这种关系的理解，将有利于学生对图形整体的认识．

（2）问题形式．

问题形式是指一个问题呈现的方式，是一个问题的外在表现形式．为方便统计分析，试将符号形式、口头形式、视觉形式依次编码为A、B、C，组合形式则为这3种形式的两两组合或3个组合，如表6．

表6 3个版本教材中“认识三角形和四边形”内容的 习题之问题形式

由表6可知，3个版本教材主要是以视觉形式或视觉形式组合其它形式为主，而几乎没有运用口头形式或口头形式组合其它形式的，这一方面与几何概念较抽象，需要借助具体的图像呈现来帮助学生理解题意、解决问题有关，具有一定的合理性；同时，这也反映出在3个版本教材中，“认识三角形和四边形”的习题更多偏向的是数学语言的表达而不是生活语言或在生活情境中的运用．

（3）问题结构．

为方便数据统计，对问题结构的3个要素进行编码，如表7．其中X表示条件开放，也即条件不确定；Y表示结论开放，也即结论不确定，Z表示策略开放，也即策略不唯一．

表7 3版本教材中“认识三角形和四边形”内容的 习题之问题结构

由表7可知，3个版本教材中“认识三角形和四边形”内容的习题之问题结构主要以封闭问题和半开放问题为主，这与学生的思维发展水平和数学学习能力相适应，难度比较适中．且就半开放问题而言，策略开放式问题较多，这说明教材意图让学生掌握解决问题的方法．

（4）思维水平．

对习题思维水平的分析，可以考查每一习题对于学生思维发展的要求．同时，也能帮助判断这些习题所要求的思维水平是否适应小学阶段学生思维发展水平，是否有利于促进学生的数学学习．采用范希尔理论的几何思维水平划分法，根据具体类目化的描述，对问题提问所体现的每一思维水平进行统计分析（可参见表8）．

表8 3个版本教材中“认识三角形和四边形”内容的 习题之思维水平

由表8可知，3个版本教材的习题之思维水平主要集中在前3个层次，这与学生的认知水平较为吻合．尽管人教版和北师版涉及“形式化演绎水平”的习题不多，但苏教版则完全没有．

4 研究结论与讨论

基于上述分析与比较的结果，可以得出如下一些基本的研究结论，并就此展开对“图形认识”（尤其是“三角形和四边形的认识”）部分的教材编写的进一步探讨．

4.1 研究结论

（1）内容呈现：既关注到儿童的生活实际，又关注到图形整体关系的认识．

一般而言，图形的认识较多从学生的生活或已有经验出发来帮助学生认识抽象的几何图形，这一点在人教版和苏教版教材中都有着充分体现．譬如，人教版教材比较注重学生从生活积累的视觉感知和实际体验出发积累空间观念．在“认识三角形和四边形”中，例题都会选择一些学生熟悉的生活实物以勾勒图形形状，直观呈现图形，意在借助学生对这些生活实物的视觉感知，为学生从整体轮廓识别图形提供支持．再有，在分别认识三角形的稳定性和平行四边形的不稳定性时，教材不仅通过简单的拉动对角或摆小棒的活动发现这一特点，还从生活实用的角度解释了三角形和平行四边形这一特性的生活意义．除此之外，北师版教材的编排给图形的认识提供了另一个导向，在其内容呈现中，较为关注图形的整体认识和关系认识．譬如，在“认识三角形和四边形”的例题内容编排中，以“图形分类”“三角形分类”“四边形分类”引入三角形和四边形的认识，并将三角形和四边形纳入整个小学阶段所认识的图形网络中，与其它图形构成上下位概念关系．

（2）编排特点：教材呈现内容具有基础性和适切性，但整体性和逻辑性相对不足．

基础性主要从知识点内容和难易度上分析其是否基本达到“图形认识”的目标要求；适切性关注学习内容和学习方式的选择是否适应学生的能力需求；整体性涉及“认识三角形和四边形”知识教学的前后联系是否紧密，学生能否完成对三角形和四边形有结构的整体认识；逻辑性体现其教材知识的逻辑是否符合学科知识的逻辑．

综合“认识三角形和四边形”的例习题分析，3个版本教材在图形认识上的基础性和适切性都较好，但整体性和逻辑性相对不足（具体表现各有不同）．就整体性而言，苏教版和人教版主要表现在图形关系认识上，北师版教材主要表现在图形要素的认识上；就逻辑性而言，人教版和苏教版教材在图形关系的认识上缺少逻辑的关联，换言之，教材在图形之间的变化关系上甚少涉及，北师版教材主要体现在图形认识的发生顺序上，即教材从直观直接过渡到图形特征和图形间关系的认识，可能会给学生学习造成一定的心智困难．

（3）对教学实践可能产生的影响．

就教师教学而言，一是影响教师对“图形认识”整体的理解．教材的内容编排可以为教师重新认识这一内容提供参考，在“认识三角形和四边形”的内容编排中，教材关于三角形和四边形的呈现一定程度上影响着教师对这一内容的整体理解．譬如，在苏教版教材中，教师可能很难把握三角形和四边形的整体关系，进而影响教师对其内部关系的深入认识．

二是影响教师对教学重点内容的把握．内容整体理解可能会间接影响教师对教学重点的把握，譬如，在北师版教材注重图形关系的认识中，教师可能会将图形关系的认识作为教学的重点，进而让学生构建三角形和四边形的内部关系．

三是影响教师教学的设计思路．基于上述两个方面，教师的教学设计思路可能会有很大的不同，譬如，按照人教版的内容编排思路，教师可能会遵从“直观认识—抽象认识图形要素和特征—应用图形要素和特征”来进行教学设计．

总之，3个版本教材对教学实践的影响可能各有不同（甚至各有利弊），所以，这就需要教师综合运用分析与比较的结果．唯有如此，教学活动才有可能促发学生在这一内容学习中数学素养的提升．其实，不同的教材内容编排“对教学实践可能产生的影响”早已发生，并且还正在继续发生．所以，真实情况与研究者基于“分析与比较”的判断是否一致，还需要进一步的实证研究来验证．

4.2 讨论

就“图形认识”（尤其是“三角形和四边形的认识”）这一内容而言，其教材编写应整体把握图形认识的5个维度（直观认识概念、定义、构成要素、特点和关系），兼顾直观认识与数学内容的本质探寻，以及注重学生几何直观与逻辑推理能力的培养．就“整体把握图形认识的5个维度”而言，图形认识的5个维度是一个系统的整体，且其间具有一定的逻辑关联，图形的认识往往从直观出发，经历逐级的抽象，从而建构起关于图形的整体结构．教材编排要从图形认识的整体出发，适应学生思维发展的阶段和水平，按照层级有逻辑地呈现几何教学内容，以帮助学生逐步建立起清晰的图形认识的思维结构．就“兼顾直观认识与数学内容的本质探寻”而言，数学概念来自一定的生活背景，生活经验可以对数学的某些对象进行合理解释．但与此同时，生活经验也会带来一些认知上的冲突，因此需要加强数学眼光的提升，需要从某一“图形与几何”的内容出发，努力探寻这一内容更为重要的数学本质．就“注重学生几何直观与逻辑推理能力的培养”而言，几何直观和逻辑推理是同等重要的．因此，在教材内容编排中需适当增加相应的习题，培养学生在图形认识的基础上进行初步的逻辑推理的训练．

教材内容编排的分析与比较，其目的不在于判断某个版本教材的好坏或者优劣，重要的是通过分析，可以整体把握某版本教材的内容呈现、编排思路和内容展开的具体进程，及其所具有的特点或特色，甚至对教学设计或实践可能产生的影响（启发或建议）；基于分析基础上的比较，可以学习或借鉴不同版本教材的特色或特点，为教育工作者开展教学设计或实践提供更为广阔的视野或启发．其实，教材的分析与比较是落实“用教材教，而不只是教教材”理念的必由之路，更是其必经之法．否则，缺乏分析与比较教材的“用教材教”只能是“蜻蜓点水”或“隔岸观火”，落不到实处，根本解决不了问题．

[1] 洪汉华．加强实验操作 培养空间观念——《三角形、平行四边形和梯形》教学建议[J]．江西教育，1993（Z1）：81-82．

[2] 蒋守彬，袁文华．《三角形、平行四边形和梯形》单元教学建议[J]．小学教学参考，2000（3）：26．

[3] 张永学．解读透教材，着力发展学生的空间意识——以《三角形、平行四边形和梯形》的教学思考为例[J]．数学教学通讯，2018（34）：61-62．

[4] 董美荣．试论以学生为本的小学数学概念教学——以《三角形的认识》为例[J]．数学之友，2015（6）：38-39．

[5] 蓝艺明．深度体验：小学数学概念教学的积极追求——“三角形的认识”教学思考与实践[J]．教育科学论坛，2017（34）：41-43．

[6] 段安阳，孙妤．教会学生用联系的观点看问题——特级教师朱国荣“三角形的认识”精彩教学片断赏析[J]．小学数学教育，2011（3）：13-14，29．

[7] 陈培群，马亚琴．化静为动，让课堂多一份情趣——“三角形和四边形”教学实践与探索[J]．小学数学教师，2014（12）：17-22．

[8] 张勇成．充实活动体验 培养空间观念——“三角形、平行四边形和梯形”教材透视及教学思考[J]．小学数学教育，2015（10）：24-26．

[9] 黄红成．在动手实践中实现真正的数学理解——以苏教版四年级下册《三角形、平行四边形和梯形》的教学为例[J]．教学与管理，2015（20）：46-48．

[10] 蒋敏杰．小学数学“图形认识”教学的目标立意与实施策略[J]．中小学教学研究，2019（2）：8-14．

[11] 徐斌艳．高中数学教材探究内容的分析指标体系及比较研究[J]．课程·教材·教法，2012，32（10）：35-40．

[12] 宋运明，邝孔秀．数学教材内容的螺旋式编写方式研究——以“平行四边形”为例[J]．数学教育学报，2018，27（6）：44-49，66．

[13] 宋运明．中国初中数学教材中勾股定理内容编写特点研究[J]．数学教育学报，2017，26（3）：44-48．

[14] WANG D C. A comparative study of geometry in elementary school mathematics textbooks from five countries [J]. European Journal of Stem Education, 2016, 1 (3): 1-10.

[15] 李鹏．“中国”“美国”“巴西”数学教材“比和比例”内容的比较研究[J]．数学教育学报，2016，25（6）：46-50．

[16] 戴再平．时代的呼唤——数学开放题研究进展综述[J]．中学数学教学参考，1999（4）：19-21．

Analysis and Comparison of the Content Arrangement of “Understanding Triangles and Quadrilaterals” in Primary School Mathematics Textbooks——With a Focus on the People’s Education Press Edition, Jiangsu Education Press Edition, and Beijing Normal University Press Edition

XU Wen-bin1, PENG Liang2, REN Li-ping1, XIE Chun-yan1, WANG Guo-hong1, ZI An-qi1, LIN Min-ting1, LIU Yan-jie1, XUE Yue1

(1. Institute of Curriculum and Teaching, Nanjing Normal University, Jiangsu Nanjing 210097, China;2. Nanjing Xiaozhuang University, Jiangsu Nanjing 211171, China)

Understanding triangles and quadrilaterals is a very important topic in primary school mathematics. Accordingly, the corresponding content in the primary school mathematics textbooks of the People’s Education Press Edition, Jiangsu Education Press Edition, and Beijing Normal University Press Edition were analyzed and compared along vertical and horizontal dimensions. Through a vertical analysis and comparison, it was found that a similarity shared by the three editions of the textbook series is that the number of right-angled triangles, rectangles, and squares is the largest, all of which are concentrated in the fourth and fifth grades. Among the quadrilaterals, the rhombus, kite shape, general trapezoid, and general quadrilateral appear more frequently. The difference is that different triangles and quadrilaterals are distributed differently across different grades. Through a horizontal analysis and comparison, it was found that the three editions have big differences in the organization of sample questions; in the context creation of sample questions, the situation types of the People’s Education Edition and the Jiangsu Education Edition are more consistent, whereas the Beijing Normal University Edition has relatively few real situations; the learning process of the sample questions is roughly the same; the thinking level of the sample questions is mainly focused on the visual and analytical level; the content organization of the exercises is relatively similar; the problem form of the exercises is mainly expressed in visual form or a combination of visual form and other representations; the problem structure of the exercises is mainly based on closed and semi-open problems; and the thinking level of the exercises is mainly concentrated on the level of perception, analysis, and informal deduction. Thus, it is recommended that the development of textbooks requires an overall grasp of the five dimensions of graphic understanding, taking into account intuitive understanding and the exploration of the nature of mathematical content while paying attention to the cultivation of students’ geometric intuition and logical reasoning ability.

primary school mathematics textbook; People’s Education Edition; Jiangsu Education Edition; Beijing Normal University Edition; recognizing triangles and quadrilaterals; analysis and comparison of content arrangement

G622

A

1004–9894（2021）02–0001–07

徐文彬，彭亮，任利平，等．小学数学教材中“认识三角形和四边形”的内容编排分析与比较——以“人教版”“苏教版”“北师版”为例[J]．数学教育学报，2021，30（2）：1-7．

2020–10–11

全国教育科学规划课题——中小学STEM教育基本理论与本土实践问题研究（BHA180126）

徐文彬（1966—），男，安徽宣城人，教授，博士生导师，主要从事数学教育和教学论研究．

[责任编校：周学智、陈汉君]