基于Copula函数的边坡可靠度高效分析方法

方 旭，冯晓波

（1.武汉大学水资源与水电工程科学国家重点实验室，武汉430072；2.武汉大学水工岩石力学教育部重点实验室，武汉430072）

0 引 言

近年来，基于可靠度理论的分析和设计方法在岩土边坡工程的安全性评价中越来越受到重视。在英美等一些国家，岩土设计规范正渐渐向可靠度设计转变［1，2］。陈祖煜等［3］认为，我国岩土工程分析与设计也应往可靠度分析方向发展。作为一种常见的岩土结构物，边坡的稳定性分析是岩土工程中一个重要的工作。边坡岩土性质多变，其各部分岩土参数（比如岩土抗剪强度参数）存在不确定性。传统的确定性分析将土体参数视为唯一确定值［4］，以有限元、极限平衡法等方法计算得到单一的边坡安全系数为依据进行边坡稳定性的评估，忽略了测量误差以及土体不均匀性等不确定性因素，导致分析结果不合理。因此，应对岩土边坡进行边坡稳定性可靠度分析［5，6］。

对边坡稳定进行可靠度分析，往往需要事先获得岩土体物理力学参数的概率分布函数。同时，已有研究表明，岩土体物理力学参数间具有明显的相关关系，且有着不同的相关结构。如岩土体抗剪强度参数间具有很强的统计负相关性［7-9］，土体剪切应力参数间也有负相关性。为了计算简便，很多情况下涉及相关变量的可靠度计算只依靠参数的边缘分布进行可靠度分析，忽略了参数间的相关性。文献［7］-［9］研究发现岩土体抗剪强度参数间负相关性对边坡稳定性有很大影响，忽略这种负相关性将会低估边坡可靠度，导致边坡设计方案不经济。也有研究考虑了相关性，但是将相关结构默认为高斯相关结构，运用Nataf变换解决相关非正态变量的独立化问题，与实际上参数间的相关结构可能并不符合，这样取得的分析结果不准确。

近年来，表征参数间相关性的Copula 函数在岩土工程可靠度研究领域被广泛用于构建含多种相关结构的随机变量间的联合概率分布函数。如唐小松［10］等学者采用Copula 函数表征了抗剪强度参数间的相关性以及构建了基桩荷载位移双曲线参数间的联合概率模型。在这一情形下，需要发展基于Copula函数构建了参数间的联合概率分布模型的边坡可靠度分析方法。目前的研究中，极少有学者研究含多种相关结构随机变量的边坡可靠度分析方法。仅唐小松［10］等在应用Copula 函数表征参数间相关性后，运用直接积分法或者直接蒙特卡洛方法来计算边坡可靠度。直接积分法在遇到高维且具有复杂表达式的可靠度问题时，失效概率计算将不能实现［10］。直接蒙特卡洛方法效率低，尤其在小失效概率水平时，计算非常困难。因此，亟须发展考虑了变量间的多种相关结构的边坡可靠度高效分析方法。

常用的蒙特卡洛模拟方法除了直接蒙特卡洛方法（MCS）外还有蒙特卡洛重要抽样法（ISM）以及子集模拟方法（SS）。蒙特卡洛重要抽样法是在直接蒙特卡洛方法的基础上通过改变抽样中心令抽样样本更大概率地落入失效域中，从而减少抽样数量，提高计算效率；子集模拟是在直接蒙特卡洛方法的基础上通过引入合理的中间失效域，将小失效概率转换为一系列容易实现的较大条件失效概率的乘积，逐层筛选，大大减少了抽样数目。而子集模拟方法在岩土边坡工程的应用中很少［11］，仅曹子君［12］做了基于子集模拟方法的边坡可靠度分析，且文献［12］中没有考虑岩土体参数间的相关性和相关结构；文献［12］中用Nataf解决非正态相关变量的变换问题，将变量间的相关结构默认为高斯相关结构，并没有考虑参数间不同相关结构对结果的影响。本文在采用Copula 函数表征参数间相关性的基础上，将重要抽样法和子集模拟方法用于含多种相关结构相关随机变量的边坡可靠分析，提出了高效地实施含有相关结构随机变量的边坡可靠度计算的方法。

1 基于Copula 函数的边坡可靠度直接蒙特卡洛方法和高效分析方法

1.1 基于Copula 函数的边坡岩土体参数联合概率分布模型

Copula 理论最早由Sklar 于1959年提出。Copula 函数是将参数的联合分布函数与其边缘函数联结在一起的函数，不受边缘分布类型的影响，可以构造出具有任意边缘分布类型和任意相关结构的联合分布函数。岩土边坡工程参数常常是二维参数，如抗剪强度参数。所以本文以二维参数为例运用Copula 函数构造岩土体参数的联合概率分布模型。根据Copula 理论，参数X1和X2的联合概率分布函数F（x1，x2）及联合概率密度函数f（x1，x2）分别为：

式中：u1=F1（x1）和u2=F2（x2）分别是参数X1和X2的边缘分布函数；f1（x1）和f2（x2）分别是参数X1和X2的边缘密度函数；C（u1，u2；θ）和D（u1，u2；θ）分别是Copula 函数的分布函数和密度函数；θ为Copula函数的相关参数。

由式（1）和（2），已知参数X1和X2的边缘分布和参数间的相关性就可以构造参数X1和X2的联合概率分布模型。由于岩土体参数间有较强的统计负相关性，而且相关结构基本是对称的，本文依据这种特性选取了4 种比较适合描述岩土体参数间相关关系的4 种Copula 函数：Gaussian Copula、Frank Copula、No.16 Copula和Plackett Copula。其中Gaussian Copula 所表征的相关结构即为常用的二维正态或者Nataf 变换中隐含的高斯相关结构。有关这4种Copula函数的概率分布函数和参数取值范围参见文献［10］。

由上可知，采用Copula 函数可以表征边坡岩土体参数间的任意相关结构（包括采用Gaussian Copula 构建的高斯相关结构和采用其他类型Copula 函数构建的非高斯相关结构），从而建立起岩土体参数的联合概率模型。接下来进行可靠度分析的关键，就是选择合适的可靠度分析方法。本文重点提出和上述概率模型结合的蒙特卡洛重要抽样方法（第1.3 节）和子集模拟方法（第1.4 节）。同时介绍了已有的直接蒙特卡洛方法（第1.2节），以供和其余两种方法对比分析。

1.2 基于Copula函数的直接蒙特卡洛方法

在进行简单失效模式的边坡可靠度计算时，直接蒙特卡罗模拟方法能得到精度较高的结果。直接蒙特卡洛方法的计算过程如下面所叙述的3个步骤：首先，模拟出服从给定Copula函数构造的参数联合分布模型的岩土体参数的N个样本点；然后，将上述模拟的样本点代入边坡失效模式中计算相应的功能函数响应值；最后，统计失效样本数目L从而得到失效概率的无偏估计值Pf=L/N。为了满足计算的失效概率变异系数小于10%，一般样本数量需大于100/Pf，因此当失效概率Pf很小时，需要的抽样样本数量N很大，计算效率很低。

1.3 基于Copula函数的蒙特卡洛重要抽样方法

直接蒙特卡洛方法编程简单，概念清晰，容易实现，但对于低失效概率边坡可靠度分析问题，其计算效率非常低［13］。很多研究人员致力于提高蒙特卡洛方法的抽样效率，提出了重要抽样法。其基本思想是提高随机样本出现在贡献率较大的“重要区域”的频率，从而提高抽样效率。基于这个原理我们可以将随机抽样密度中心取在设计点上，因为设计点是失效边界上对失效概率贡献最大的点［12］。而设计点可由一次可靠度方法求得。本文借鉴这一方法，将其应用于采用Copula 函数表征了参数间相关结构的边坡可靠分析中。取正态分布密度函数px为重要抽样密度函数，以设计点为抽样中心，对参数X抽样，得到样本Xi=（xi1，xi2，…，xin）（i= 1，2，…，N），则Pf的无偏估计值为：

式中：I(x)为示性函数，当x＞0 时，I（x）=1；当x≤0 时，I（x）=0；fX（X）为参数X的联合分布密度函数，结合Copula 函数，可由基于Copula 函数构造的参数间联合密度函数［即式（2）］代替，将其带入式（3）中即可求得失效概率。

1.4 基于Copula函数的子集模拟方法

子集模拟方法最早由Au 和Beck［14］提出，通过引入中间失效事件，将小失效概率用一系列较大的条件失效概率的乘积表示。子集模拟方法可以一层一层快速逼近功能函数失效域，快速寻找最终失效域，大大降低随机抽样数目，从而提高了可靠度分析效率，抽样过程不涉及设计点的寻找，相比于重要抽样法，进一步提高了计算效率，且不会产生维数灾难，可以更高效率地分析小失效概率岩土边坡稳定性。考虑到边坡岩土体参数间含有相关性，且相关结构类型不定，本文提出基于Copula函数的子集模拟方法来进行边坡可靠度分析。子集模拟概念及实现过程如下：

设岩土边坡失效临界响应值为b，失效域F定义为F=｛g≤b｝。使中间事件满足嵌套关系：F1⊃F2⊃…⊃Fm=F，那么目标失效概率可以表示为：

选取中间事件Fi=｛g≤bi，i=1，2…m｝，m为中间事件总数，中间事件条件概率P(Fi|Fi-1)足够大，即可以保证高效地模拟PF。设条件失效概率为P0=P（Fi|Fi-1），取P0=0.1，那么由式（4）可得：

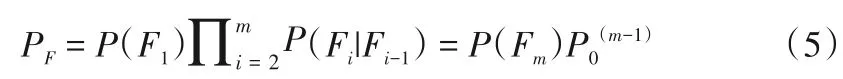
可以看出，当PF为10-4量级的时候，只需要四轮抽样，每轮抽样100个即可达到目标概率，而直接蒙特卡洛方法需要105个抽样样本才能达到目标失效概率，子集模拟极大提高了抽样模拟效率。与Copula函数结合，该方法的具体实现过程如下：

（1）通过蒙特卡洛随机抽样得到n组相互独立的标准正态分布随机变量V=｛（V1i，V2i），i=1，2，…，n｝，通过反变换，利用Copula 函数表征的参数概率联合分布模型，将V变换为n组服从给定Copula 函数相关结构的样本X=｛（X1i，X2i），i=1，2，…，n｝，将X带入功能函数g，得到一系列功能函数响应值，并将响应值按由小到大排序，取第nP0个功能函数相应值为中间事件域值bi。前nP0组样本是落入第一个失效域F1=｛g≤b1｝的样本点。失效概率为P（Fi|Fi-1）=P0=0.1。

（2）分别利用Metropolis-Hastings 算法以落在失效域Fi-1中的样本点Vi-1为“种子”，产生1/P0组新样本Vi。

（3）通过步骤（2）产生的nP0/P0=n组样本V，通过Copula 函数构造的参数X1和X2的联合概率密度函数将V变换为n组符合样本相关结构和相关关系的样本X=｛（X1i，X2i），i=1，2，…，n｝带入功能函数g计算功能函数响应值，将功能函数响应值按从小到大排序，以第nP0个功能函数值为中间事件阈值bi。

（4）重复（2）、（3）步，直到第m层有超出nP0个功能函数值小于零时，终止重复。

（5）统计第m层落入失效域Fm的样本组数NF，则可以计算出失效概率为PF=（NF/n）P0（m-1）。

2 功能函数为显式表达式的边坡可靠度分析

本节将所提的考虑了参数间相关结构的高效可靠度分析方法（即重要抽样法和子集模拟方法）用在功能函数为显式表达式的边坡。

2.1 边坡分析模型

以文献［15］中的一个功能函数为显式的算例进行分析，基本资料：边坡岩体的岩质成分为红色黏土层（SC）、紫红色矽质岩（SQ）以及震旦纪矽质的云岩（SLS），如图1。该边坡岩体发育有一组顺坡产出缓倾角节理，平均产状为N70oE/SE∠30o，贯通层面程度不高，岩体结构为顺坡层状结构。边坡岩体节理与黏土岩层面可能构成双滑面剪切破坏模式，前者为被动滑面，后者为主动滑面。

图1 边坡岩体稳定分析简图Fig.1 Diagram of slope rock mass analysis

采用刚体极限平衡法计算边坡安全系数FS，据此可得边坡稳定可靠度分析功能函数为：

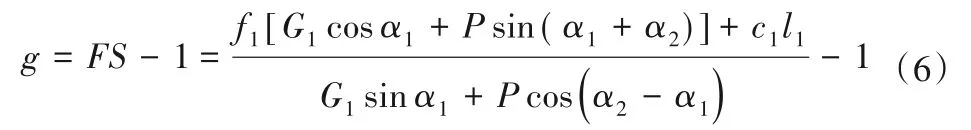
其中：

式中：G1和G2为块体重量；c1和c2为滑动面上的黏聚力；f1和f2为滑动面上的摩擦系数；l1和l2为块体基面长度。

将f1、f2、c1、c2、α1、α2视为随机变量，其中f1、f2、c1、c2根据室内试验数据确定，服从对数正态分布，α1和α2根据现场试验数据确定，服从正态分布，统计参数见表1。确定性参数取值为：块体重量G1=46 669 kN，G1=34 274 kN；块体基面长度l1=67.2 m，l2=96.8 m；岩体重度γ=27 kN/m3。运用本文用所提的方法：基于Copula 函数的蒙特卡洛重要抽样法、基于Copula 函数的子集模拟方法计算该显式岩质边坡的失效概率。为了验证所提方法计算得到的失效概率的准确性，也采用直接蒙特卡洛方法计算了该边坡的失效概率，供对比分析。用4 种Copula 函数（Gauss⁃ian、Frank、No.16 和Plackett）表征相关性，目的是为了对比分析参数间相关结构对可靠度计算结果的影响。为了简化计算过程，设f1和c1及f2和c2两对参数的相关系数相同，α1和α2相互独立。设定参数间的相关系数为-0.5。计算结果如表2所示。

表1 边坡滑动面强度参数的统计特征Tab.1 Statistical characteristics of strength parameters of sliding surface of slope

2.2 边坡可靠度高效性分析

表2中，以N=1×106次直接蒙特卡洛方法计算的可靠度指标为准确值，同时比较了4 种Copula 函数相关结构下的3 种可靠度方法。从表2可以看出，同种相关结构，蒙特卡洛重要抽样方法误差小于20%，子集模拟方法误差小于6%，说明了本文所提方法的有效性和准确性；在模拟效率上，基于Copula 函数的重要抽样法只要1×104次就能得到准确的结果，效率是直接蒙特卡洛的100倍，是高效的边坡可靠度分析方法；基于Copula函数的子集模拟只用了200 次就可以得到相对准确的结果，这说明在计算精确度较好时，子集模拟效率相比直接蒙特卡洛法和蒙特卡洛重要抽样法有很大提高。

表2 不同可靠度计算方法的边坡可靠度结果Tab.2 Results using different slope reliability methods

2.3 不同相关结构结果对比分析

对比不同相关结构的结果的差异时，相关系数从-0.1 到-0.9 变化，采用最高效的子集模拟方法计算的结果作比较，如图2。可以看出，本算例中采用不同Copula 函数计算的失效概率存在差异，这是由于考虑了随机变量间不同相关结构的结果。No.16 Copula 函数计算的失效概率高于其他3 种Copula 函数计算的失效概率，其他3种Copula函数的计算结果十分接近。若以No.16 Copula 函数计算的结果为准确值，Gaussian Copula、Plackett Copula 和Frank Copula 函数计算出来的失效概率偏低，采取这3种Copula函数的计算结果进行可靠度设计会使设计不经济；若以Gaussian Copula 函数计算的失效概率为准确值，运用No.16 Copula 函数计算出的失效概率结果偏高，采取No.16 Copula 函数方法进行可靠度设计会导致设计不安全。因此，运用Nataf 变换（即认为边坡岩土体参数间隐含高斯相关结构）的做法可能使得计算结果不准确，而基于Copula 函数，可以考虑边坡岩土体参数间任意相关结构，得出更符合实际的边坡失效概率。同时，我们可以看出，该岩土边坡的失效概率随着相关系数的绝对值增大而减小，说明岩土参数间的负相关性对岩土边坡的稳定性有积极影响，忽略这种相关性会导致岩土边坡可靠度设计不经济。

图2 考虑不同相关结构时边坡可靠度的比较（子集模拟计算结果）Fig.2 Results of subset simulation considering different related structures（SS results）

3 功能函数为显式表达式的边坡可靠度分析

上一节中边坡的功能函数为显式函数关系。下面以四川省大岗山水电站左岸边坡工程为例［10］说明本文所提方法在功能函数为隐式函数的边坡可靠度分析中的有效性。

3.1 边坡分析模型

大岗山水电站位于四川省西部大渡河中游石棉县境内［10］，坝址处控制流域面积达6.27 万km2，占全流域的81%，多年平均流量1 010 m3/s，是大渡河干流近期开发的大型水电工程之一，电站装机容量2 600 MW，最大坝高210 m，电站正常蓄水位1 130 m，总库容7.42 亿m3.该电站地理位置上处于川滇南北向构造带北段，为北东向、南北向与北西向等多组构造的交汇结合部位。坝区位于由磨西断裂、大渡河断裂和金坪断裂所切割的黄草山断块西侧边缘，大地构造部位属扬子淮台地西部二级构造单元康滇地轴范畴。坝区河谷深切，呈Ω 形嵌入河曲形态，其新构造运动总体表现为以整体间歇性强烈抬升为主，有作用方向表现为NWW-SEE 向挤压的区域构造应力场。已有测试结果显示，大岗山坝区应力场是自重力和构造应力叠加的应力场，且构造应力是坝址左岸应力场的主要组成部分。该边坡边坡稳定性问题突出，其中、陡倾角的顺坡向节理裂隙较为发育，具有卸荷风化强烈、高地应力以及高地震烈度的特点。在不加固情况下，一点小的外来荷载，就很可能产生规模巨大的滑坡和山体变形。大岗山水电站坝址50年超越概率10%基岩水平向加速度为0.251 g，相应的地震基本烈度为VIII 度。通过分析坝区VII～VII 剖面左岸天然边坡（见图3，图中符号V2、V1、IV、III1、II 为岩体质量分级），发现岩脉β28和断层f68切割边坡岩体组合成潜在滑动体。将岩脉β28的抗剪强度f1和c1，断层f68的抗剪断强度f2和c2视为对数边坡岩体重度为γ=25 kN/m3，左岸边坡滑动面强度参数统计特征值见表3。

图3 坝址区VII～VII剖面左岸天然边坡Fig.3 Left natural slope of dam site section VII～VII

表3 左岸边坡滑动面强度参数的统计特征Tab.3 Statistical characteristics of the strength parameters of the sliding surface of the left bank slope

计算该边坡稳定性时考虑3种工况：天然工况（不考虑降雨和地震因素）、降雨工况（地下水位高度取为滑体高度的10%）、VIII度地震工况（计算中水平向地震加速度为0.251 g）。边坡稳定安全系数采用刚体极限平衡法中的剩余推力法计算，需要反复迭代才能求得，极限状态方程g=FS-1=0，即没有显式表达式。运用本文所提的基于Copula 函数的蒙特卡洛重要抽样法和基于Copula 函数的子集模拟方法计算该隐式岩质边坡的失效概率。为了验证所提方法计算得到的失效概率的准确性，也采用直接蒙特卡洛方法计算了该边坡的失效概率，供对比分析。此外，为了简化计算，设f1和c1及f2和c2两对参数的相关系数相同，在对比不同可靠度计算方法时设定相关系数为-0.5 不变，计算结果如表4、表5和表6。

3.2 边坡可靠度高效性分析

由表4、表5和表6所示的任意一种工况的计算结果可以看出，以直接蒙特卡洛方法计算的失效概率为准确值，同一种Copula 函数相关结构条件下，蒙特卡洛重要抽样方法和子集模拟方法都能得到相对准确的结果，绝大部分情况失效概率计算结果误差小于20%，精度最差的为降雨工况时蒙特卡洛重要抽样法计算的结果，误差为38.46%，说明了本文所提方法处理含隐式功能函数表达式的边坡可靠度问题的有效性；在模拟效率上，蒙特卡洛重要抽样方法相比于直接蒙特卡洛方法，抽样次数是其1%，效率很高；而子集模拟方法的抽样模拟次数仅需800～2 000 次，相比于蒙特卡洛重要抽样方法的计算效率又进一步提高。此外，还可以看出，大岗山水电站坝址处左岸边坡在天然工况下失效概率在考虑几种相关结构的情况下最大为4.8×10-4左右，失效风险非常小，在天然状态下具有足够的安全度；而在地震工况下失效概率达到了0.27，该左岸边坡非常不安全，有必要对该左岸边坡增加锚固措施，防止失效破坏，危及人民生命和财产安全。

表4 不同方法计算的可靠度结果（天然工况）Table.4 Results of different slope reliability methods（Natural condition）

表5 不同方法计算的可靠度结果（降雨工况）Table.5 Results of different slope reliability methods（Rainfall condition）

表6 不同方法计算的可靠度结果（地震工况）Tab.6 Results of different slope reliability methods（Earthquake condition）

3.3 不同相关结构结果对比分析

同时为了对比不同相关结构对可靠度分析结果的影响，在天然工况下，设定抗剪断强度参数f1和c1及f2和c2的相关系数从-0.1～-0.9 变化，选取最高效的子集模拟方法的结果，结果如图4。由图4可以看出，随着相关系数变小，即参数间的负相关性增加，失效概率下降，说明岩土体参数间的负相关性对岩土体稳定性有积极作用。此外，不同Copula 函数计算的失效概率有着显著差异。No.16 Copula 函数计算的失效概率相比其他3种Copula 函数的计算结果较高，Gaussian Copula 函数计算的失效概率偏低。若以Plackett Copula 函数计算的失效概率为准确值，运用No.16 Copula 函数的计算结果对该进行边坡可靠度设计，会造成设计方案偏保守，而如果运用Gaussian Copula 函数的计算结果作该边坡可靠度设计，会造成设计方案不安全的结果。因此，运用Nataf 变换（即默认为Gaussian Copula 表征的相关性）认为边坡岩土体参数间隐含高斯相关结构的做法会使得计算结果不准确，而基于Copula 函数，可以考虑边坡岩土体参数间任意相关结构，能得出更合理的失效概率。此外，由于NO.16 Copula 函数计算的失效概率偏高，应用该函数的计算结果进行边坡可靠度设计会偏于保守，设计更安全，所以对于该类工程边坡，在进行边坡可靠度分析时建议应用NO.16 Copula函数。

图4 考虑不同相关结构时边坡可靠度的比较（天然工况，子集模拟计算结果）Fig.4 Results of subset simulation considering different related structures（Natural condition；SS results）

4 结 论

（1）引入Copula 函数表征岩土体参数间的相关性并进行边坡可靠度分析十分必要。Copula 函数可以表征参数间包括高斯相关结构在内的任意相关结构。不同的相关结构类型情况下，边坡失效概率差别较大。在岩土体参数间具体相关结构未知时，需要谨慎选取Copula 函数类型。有试验数据时，建议根据数据选择最适合的Copula 函数类型。盲目地选取任意Copu⁃la 函数都会导致设计结果不合理。尤其需要指出的是，如果为了简便而运用Gaussian Copula 函数的计算结果做边坡可靠度设计，会造成设计方案不安全或不经济。

（2）所提的含相关结构随机变量的边坡可靠度高效分析方法可以克服直接蒙特卡洛方法效率低的缺陷，且计算精度有保障。尤其是子集模拟算法在基于Copula 函数表征了变量间的相关结构的边坡可靠度分析中效率极高，只需模拟少量样本即可获得失效概率值。同时，该方法能有效处理含隐式功能函数边坡可靠度分析问题，进一步拓展了高效蒙特卡洛方法在边坡可靠度分析中的应用。

（3）大岗山水电站坝址处左岸边坡在自然工况和降雨工况下失效概率很小，一般情况下有足够的安全度；但在地震工况下的失效概率很大，应对其进行锚固支护措施提高其稳定性。□