不同降雨特征对径流过程的影响研究
朱 奎,强思远,母小苗,刘唐琼,李 杰
(中国矿业大学资源与地球科学学院,江苏徐州221116)
我国是一个幅员辽阔,地域气候差异较大的国家。由于地理位置和气候的影响,不同地区的降雨通常会呈现出不同的特征[1]。在某个区域内,由于地形,植被,气温的变化,自然降雨的雨强也会随着时间出现波动[2],尤其是在山坡丘陵地区[3]。作为河川径流的重要组成部分,坡面流的测算、预报等工作具有重要意义。而降雨是影响坡面径流的重要因素[4,5],当降雨的分布和强度发生变化时,坡面流也会呈现不同的进程。
对于降雨过程特征对坡面流的影响,目前已有大量研究[6,7],如Parsons and Stone[8]进行的5 种雨型不同,降雨量相同的模拟降雨试验,李和谋等[9]在野外模拟的3 种不同雨强的产流产沙试验等。对坡面流与下渗过程进行数值模拟[10]也是研究坡面降雨径流过程的常用方法[11,12]。但目前的研究大多只关注降雨特征中的单一因素对径流过程的影响[13],对于降雨雨型和强度耦合影响径流过程的相关结论较少,并且缺乏对整个径流过程的量化评价方法。
因此本文根据地区历史气象资料,设计两组具有不同峰值的降雨雨型,通过人工模拟降雨试验和基于运动波方程的坡面流数值模型还原降雨径流过程,选取径流过程中的径流峰值,径流总量,峰现时刻,径流总量特征值作为分析对象,研究降雨雨型和峰值对径流过程的影响。
1 材料与方法
1.1 试验设计
试验于2019年12月于江苏省徐州市中国矿业大学水文与水资源系实验室进行,模拟降雨采用喷淋式系统,设计降雨强度1~5 mm/min,雨滴降落高度1 m。微型试验槽为长宽高100 cm×40 cm×20 cm 的土槽,试验区面积为0.4 m2。分为左右宽度相同的两部分。降雨过程与出流过程分别采用霍尔水流量器与谐振式水深传感器采集。其装置示意如图1所示。
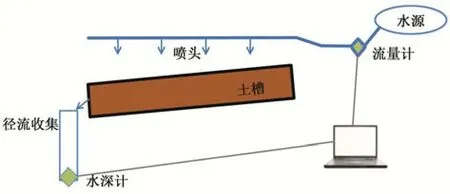
图1 模拟降雨装置示意图Fig.1 Schematic diagram of the test device
同时根据文献资料与本地历史降雨选择了1、3、4 mm/min 3 种雨强,组合为两组共4 种降雨历时均为20 min 的试验降雨过程,分别命名为前峰Ⅰ,Ⅱ型(降雨峰值集中于前期),后峰Ⅰ,Ⅱ型(降雨峰值集中于后期)。并加入一种作为对照的无峰型降雨。各降雨过程雨强随时间的变化如图2所示。
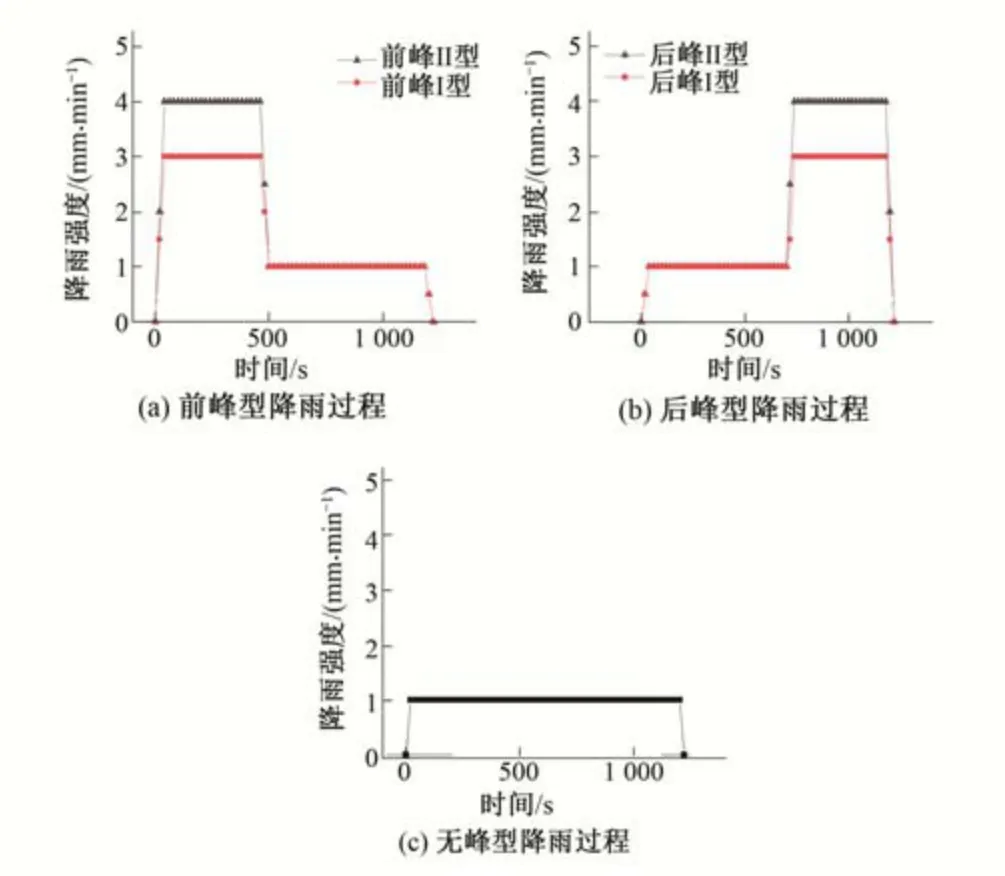
图2 设计降雨过程Fig.2 Experimental rainfall process
1.2 试验材料
试验采用土壤材料作为下垫面,土壤于2019年12月取自江苏省徐州市铜山区,每两次试验取一次土,并在每次试验前统一用烘干法对所取土壤进行含水率与容重测定,进行放置风干处理使土壤前期情况保持一致。在除去大颗粒杂物与有机质后,均匀铺入土槽并压实,使其容重保持在1.1 g/cm3,厚度保持在20 cm,坡度均为5°。经烘干过筛后测得土壤的粒径分配如表1所示。
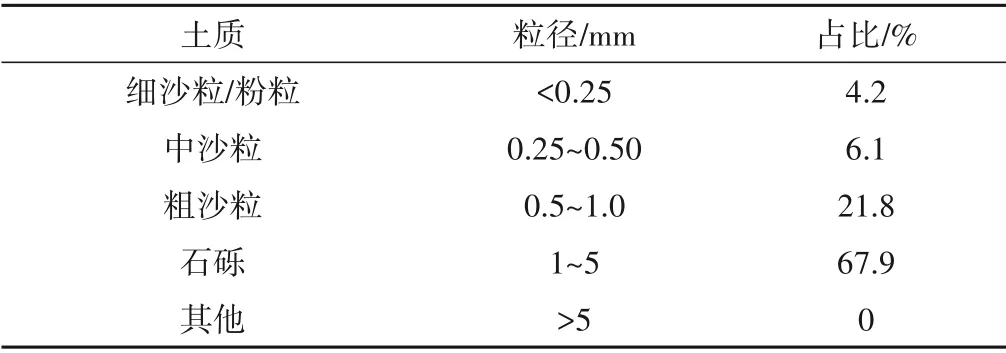
表1 试验土壤粒径分配Tab.1 Particle size distribution of test soil
1.3 模型建立
使用运动波模型描述坡表径流过程,写作:
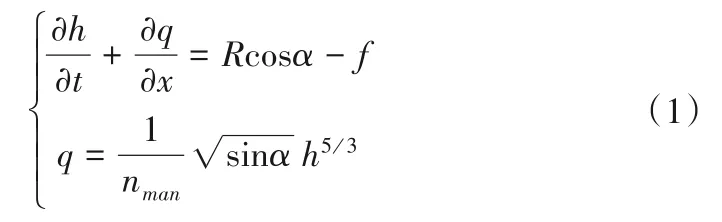
式中:h为地表径流深,m;q为单宽流量,m2/s;R为竖直方向上的雨强,m/s;α为坡脚;nman为曼宁系数;f为下渗率,m/s;x,t分别为以上部边界为起点的坐标和时间,m及s。
由于山坡表层土壤通常较薄,降雨在前期以土壤垂向一维入渗为主。随着入渗(采用霍顿下渗曲线计算)的进行,湿润峰抵达基岩不透水界面后入渗水聚集在基岩层,达到最大储流深后会产生侧向的壤中流,采用达西定律计算:

式中:v为渗透速度,m/s;Ks为渗透系数,m/s;H为坡顶和坡脚的水头差,m;L为坡面的长度,m。
2 结果与分析
由模拟降雨径流试验得到累计径流量后,对累计径流总量按取样频率进行求差,得到对应时刻的瞬时径流量,并进行均值化处理,其计算方法如式(3)所示:
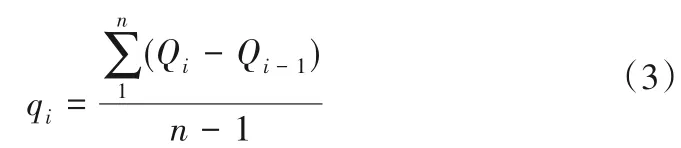
式中:qi为第i时刻的径流量,L/s;Qi为开始降雨至i时刻的径流总量,L;n为被平均的相邻时刻数,取20。
得到5 种降雨的径流过程(见图4)后。将径流过程的特征值分别提取绘出,如图3,各点横坐标分别对应无峰、前(后)峰Ⅰ型、前(后)峰Ⅱ型降雨的降雨峰值。
2.1 降雨雨型对试验径流过程的影响
由图3可知,在降雨总量一致的情况下,后峰Ⅰ型降雨的径流峰值相比前峰Ⅰ降雨少了14%,后峰Ⅱ降雨径流峰值则超过前峰Ⅱ型17%。在峰现时一项中,后峰Ⅰ型降雨的径流峰现时较前峰Ⅰ型滞后了252 s,后峰Ⅱ降雨的峰现时较前峰Ⅱ型滞后145 s。
相较于无峰型降雨,后峰型降雨的径流峰现时刻相对滞后,而前峰降雨则整体有较大提前。在径流总量上,当降雨历时和总量相同时,后峰型降雨总会比前峰型降雨多产生25%左右的径流量。与无峰型降雨相比,两种雨型产生的径流过程特征值均呈现出相同的偏移趋势,只在偏移量上有所差别。
2.2 降雨峰值对试验径流过程的影响
为了进一步探究探究不同的降雨雨型下降雨峰值对径流过程的影响,对图3各特征值随雨强变化的5 个数据点进行拟合,结果如表2所示,公式中x为降雨峰值强度,y为对应的径流特征值。
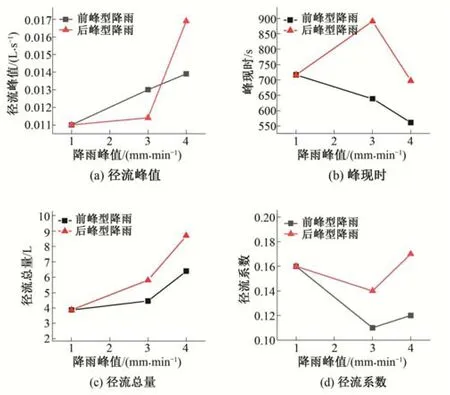
图3 不同降雨特性的实测径流特征值对比Fig.3 Comparison of measured values of runoff processes of different rainfall and rainfall patterns
据表2,两种降雨雨型的径流峰值均与降雨峰值呈正相关。而后峰型降雨的曲线更接近指数关系。各雨型的峰现时均与降雨峰值呈强负线性相关,峰值强度每上升1 mm/min,峰现时提前约40~200 s,这个值在后峰型降雨和前峰型降雨中有明显差异,而后峰型降雨的峰现时总会滞后于无峰型降雨。两种雨型的径流总量采用指数拟合的方式可以获得较好的效果,在后峰型降雨中指数增加的趋势更加明显。不论是前峰或后峰型降雨,它们的径流峰值,峰现时,径流总量和径流系数均与降雨峰值呈现出比较强的相关关系。相对于前峰型降雨,后峰降雨径流过程对降雨峰值响变化的响应更为敏感。
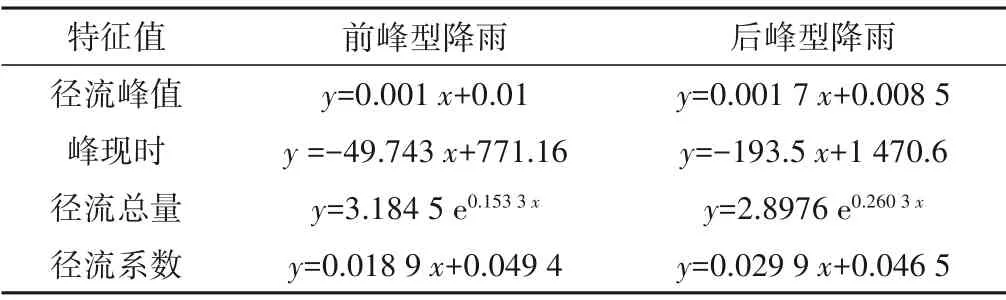
表2 特征值拟合结果Tab.2 Fitting results of characteristic values
2.3 模型验证
在试验中每种降雨试验都同时进行两次,得到两份降雨数据,其中一份用于模型参数率定,另一份则用作验证。在参数率定中,我们将问题归纳为了一个以模型纳什系数为目标变量,待率定参数为输入变量的多元函数求最值问题,采用计算机编制的遗传算法程序求解。为缩短计算时间,我们将率定算法的种群规模规定为40,最大迭代数为10。经过计算,最终主要参数取值如表3所示。
依照图2输入5 种降雨过程,并将模拟径流结果与实测径流过程进行对比,如图4所示。
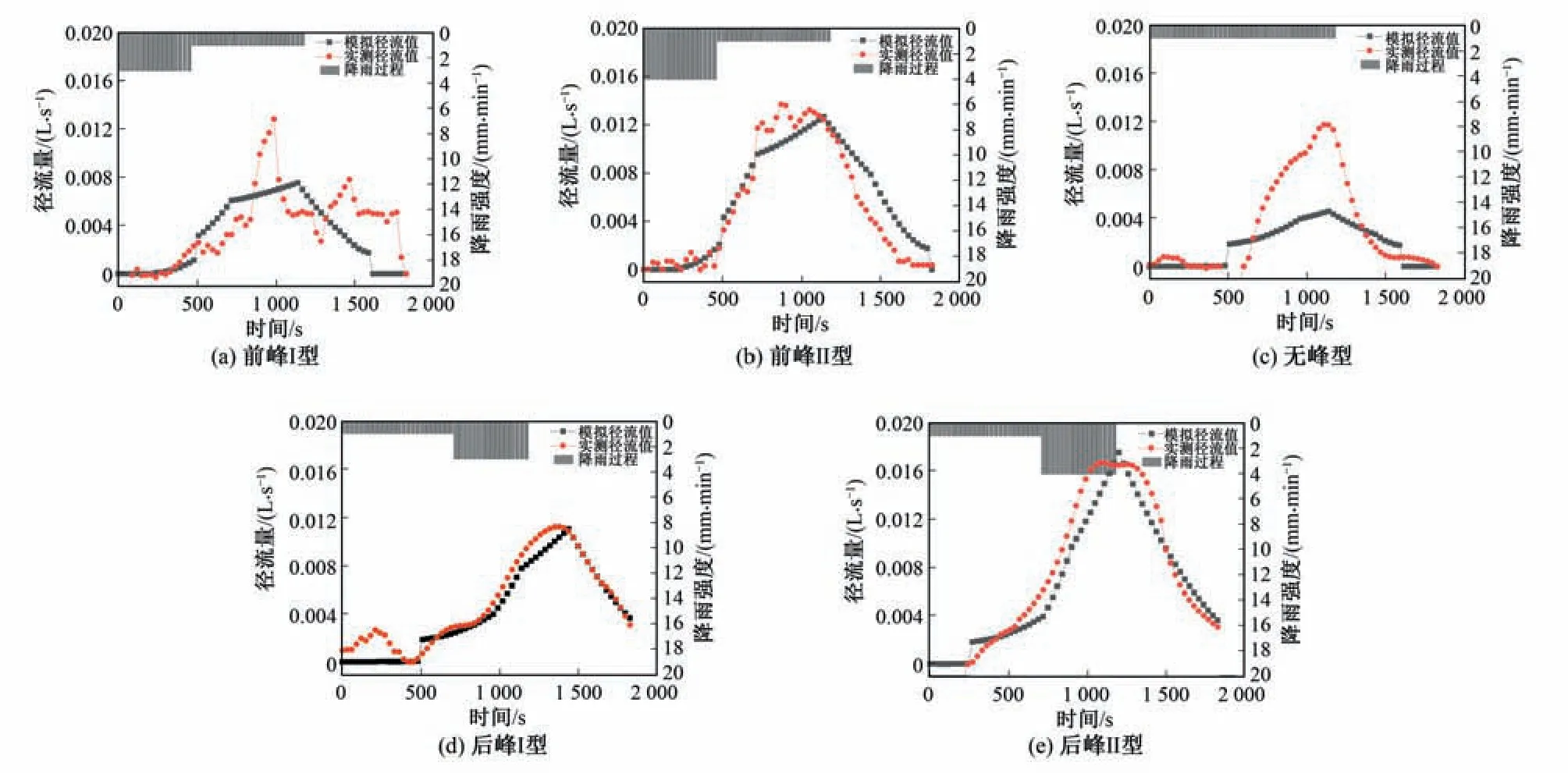
图4 不同特性降雨径流过程实测值与模拟值Figure 4 Comparison of measured and simulated rainfall runoff
表4列出了模拟值与实测值的拟合结果。可以看出数值模型对降雨较大,且降雨集中于后期时的降雨模拟效果较好。降雨量较小时效果较差。考虑到实测径流过程可能出现异常的情况,如前峰Ⅰ型的实测径流过程出现异常的剧烈波动,可能是由于某时段集水箱水位快速上升产生的水面波动导致的。此外,仪器的测量误差也可能导致测量结果的异常。考虑到这些情况,本模型基本能够较好地完成对不同降雨特征径流过程的模拟。
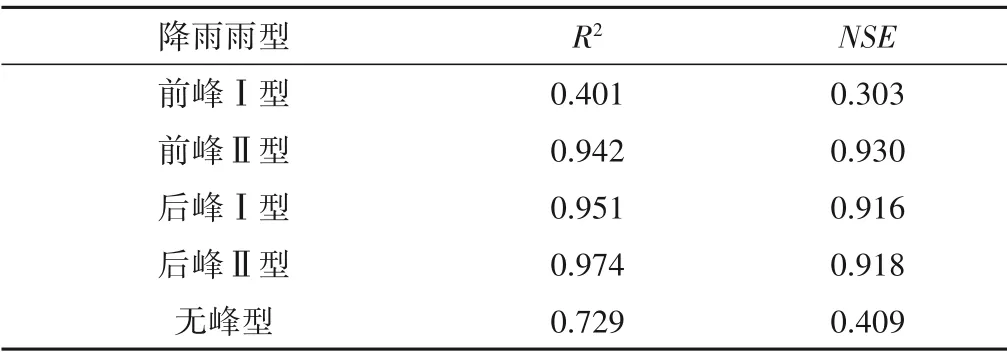
表4 径流实测值与模拟值特征值拟合度Table 4 Fitted of the measured and simulated values
2.4 降雨特征对模拟径流过程的影响
为进一步验证模型效果,与实测径流特征值一样,分别列出图4中模拟径流过程的特征值变化曲线如图5。
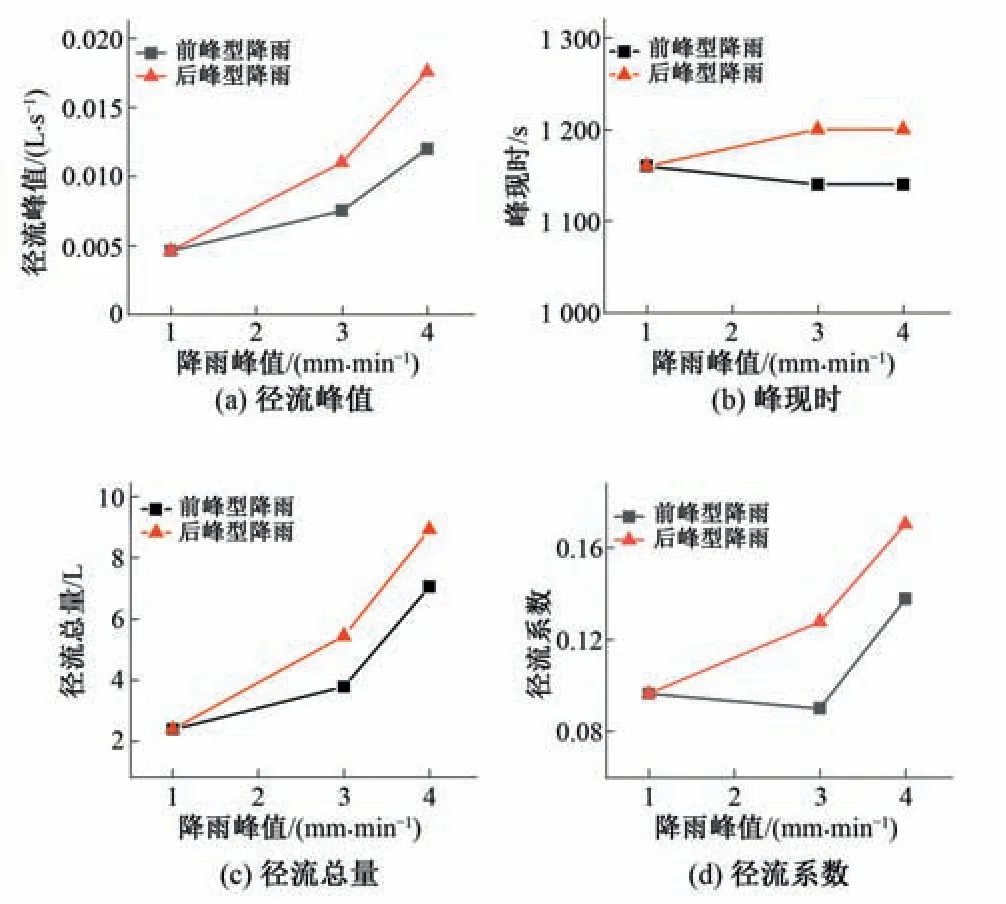
图5 不同降雨特性的模拟径流特征值对比Figure 5 Comparison of eigenvalues of simulated runoff processes of different rainfall patterns
各雨型下的模拟特征值与实测特征值基本一致,较好的还原了特征值的变化趋势。但在降雨峰值相同的情况下,两种雨型径流特征值间的差异变小,尤其是图5中峰现时并未出现显著的变化趋势,而是维持在某个固定时刻,这可能与输入降雨数据的突变有关,突变点固定导致径流过程的拐点在不同的模拟降雨径流过程中没有发生变化。
在本文所建立的降雨模型较为可信的基础上,设计12种降雨工况,分成前峰型与后峰型两大类。在1~5 mm/min 间以0.5 mm/min 的插值均匀设置降雨峰值。在目标径流特征值的选取上,由于图5中峰现时模拟结果出现异常,径流系数与径流总量高度相关,所以工况只选择径流峰值和径流总量作为模拟目标值。如图6分别为模拟的总径流量和径流峰值曲线,表5为曲线的拟合结果。
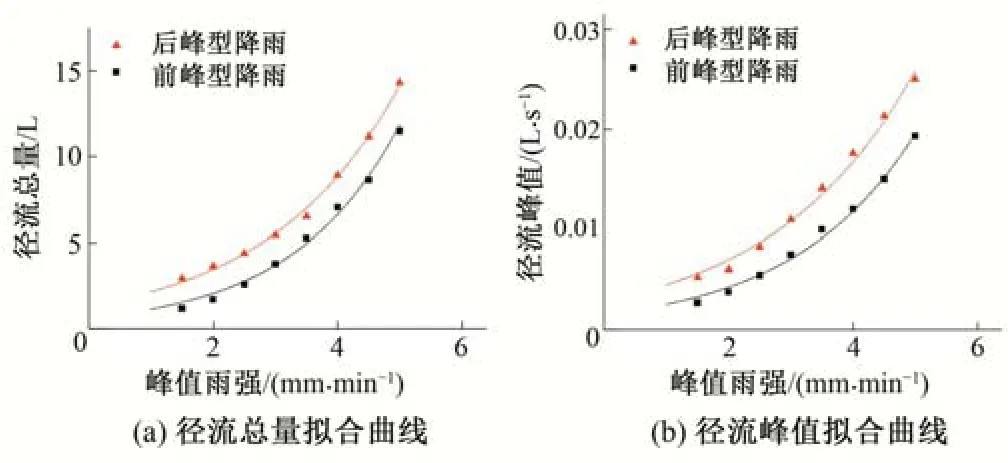
图6 模拟工况径流特征值拟合曲线Fig.6 Characteristic values of runoff process under simulated operating conditions
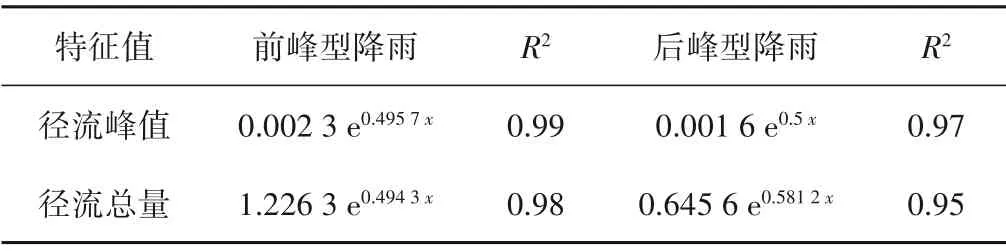
表5 模拟工况特征值拟合Tab.5 Fitting of simulated working conditions
经拟合,两种雨型的径流峰值和总径流量与降雨峰值均呈现y=Aexp(b x)形式,b值均为0.5 左右。我们可以认为这是由于峰值持续时间不变,当试验中降雨峰值增大时,总降雨量相应增大,两者叠加引起的径流特征值变化。为对其成因进行进一步分析,根据水量平衡关系,绘制了土壤含水量总量的变化过程,如图7所示。
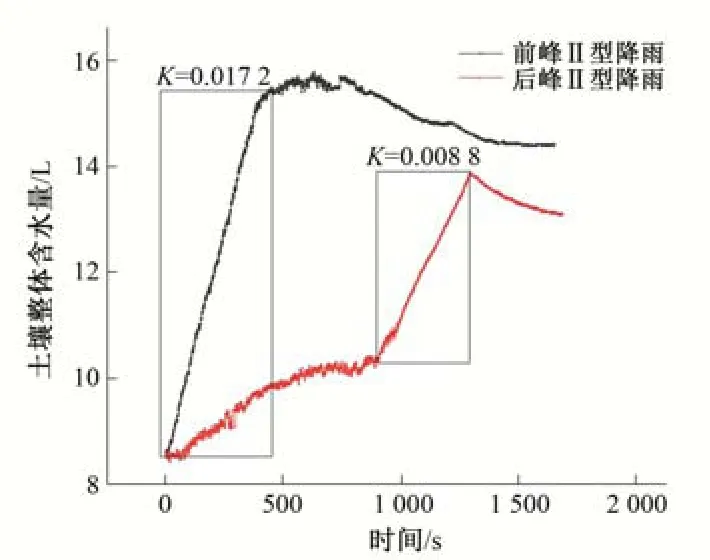
图7 前峰Ⅱ型与后峰Ⅱ型降雨土壤总含水量的变化过程Fig.7 The change process of soil moisture content of Early peakⅡ&Delay peakⅡ
以前峰Ⅱ型和后峰Ⅱ型降雨径流过程为例,两者的土壤含水量都在降雨峰值持续时期出现了一个稳定的直线上升阶段,如图7中虚线框所示。
对于前锋型降雨,由于土壤前期的下渗能力要高于降雨强度,高强度降雨可以以接近峰值降雨强度的下渗率充分入渗。这个过程在土壤含水量变化图中则显示为左侧虚线框的含水量直线上升部分。而在试验中,我们也并未在前期观察到地表径流的出现,说明降雨全部渗入土壤内。在降雨中后期,降雨强度开始变小,同时我们观察到了明显的地表径流和土壤表面积水,可以推断出虽然中后期的降雨强度较低,但表层土壤已接近饱和,下渗能力衰减迅速,此时的降雨强度要略大于土壤下渗能力,从而产生地表超渗径流。而当表层土壤达到饱和状态后,下渗率稳定,降雨与地表超渗径流和壤中流基本保持平衡状态,这表现在土壤水变化过程图中就是土壤含水量的相对稳定。
而对于后峰型降雨,其中前期的下渗过程与前锋型降雨相似,但因为降雨强度较小,土壤水含量上升缓慢。在降雨后期,表层土壤的下渗能力也不断下降,同时降雨强度上升,导致下渗能力远小于降雨强度。这在试验中表现为几乎是在雨强升高的同时,地表就开始大量积水并产流。从土壤含水量变化图中也可以看出,后峰型降雨后期引起的土壤含水量上升直线的斜率(图中右侧虚线框)与前锋降雨相比,在同样的雨强下是偏小的,这是因为此时的土壤含水量不仅要在降雨的基础上去掉壤中流,还需减去大量的地表超渗径流。
从这两个过程可以看出,在降雨峰值持续期间,后峰型降雨的下渗率要比前峰型降雨小,这就导致后峰降雨在降雨峰值持续期间下渗受阻,从而产生更大的径流峰值,同时也使后峰型降雨在整个降雨径流期间渗入土壤的降雨总量更少,产生的径流总量更大。
此外,由图6可知,在整个模拟工况范围内的径流峰值和径流量间应存在线性关系,两者经拟合后如图8所示。两种雨型的拟合曲线斜率基本相同,说明这种线性关系并不受降雨雨型的影响。
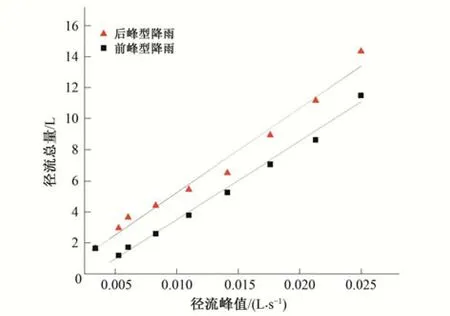
图8 径流量与径流峰值拟合曲线Fig.8 Fitted curve of runoff amount and peak
3 讨论与结论
(1)讨论。对不同的降雨雨型和峰值影响下的降雨径流过程,在场地降雨试验和数值模拟中得到了一致的结论,其中不同雨型和峰值下径流总量和径流峰值增加的趋势与一些已发表的文献中的结论一致[14,15],但在拟合出的公式形式上有较大差别。相关文献[16]认为高强度的降雨可能会破坏土壤结构,使地面板结形成土壤团聚体,阻挡降雨入渗。而在试验过程中,仅在降雨的前期有少量土壤的团聚体出现,并随着降雨进程迅速消失。在降雨后期中在土壤与土槽侧面面接触面上可以观测到明显的水流过程,表明壤中流的出现。这也可能是导致后峰型降雨径流峰值显著增大的原因。
(2)结论。①两种不同的雨型产生的径流总量和径流峰值均与降雨峰值指数相关,且呈y=ae0.5x形式,b值均为0.5 左右。当雨型相同时,一定雨强范围内产生的总径流量与径流峰值呈线性相关趋势。②与无峰型降雨相比,前峰型降雨会使径流洪峰提前,后峰型降雨会使峰现时滞后。无论哪种降雨雨型,降雨峰值的升高都会使径流峰现时提前,且呈强线性关系,即峰值强度每上升1 mm/min,峰现时提前约40~200 s,这个值在后峰型降雨和前峰型降雨中有明显差异。③在降雨量,降雨历时相同时,后峰型降雨会比前峰型降雨多产生近1/4 的径流。从降雨特征与径流过程的关系来看,峰值较大的后峰型降雨在洪水预报与水文计算中应进行着重应对与分析。 □

