基于藤Copula多维联合分布的CMIP5多模式降雨综合方法研究

胡义明，罗序义，梁忠民，刘 杨

（河海大学水文水资源学院，南京210098）

0 引 言

全球气候模式是对气候进行模拟和预测的重要工具之一［1］，常被用于未来水文情势的分析预估。耦合模式比较计划第五阶段（CMIP5）新增了一些模式试验，采用的耦合器技术、通量处理方案及参数化方案比CMIP3的更为合理，在一定程度上提高了气候模式的模拟和预估能力［2］。虽然气候模式在不断地改进和发展，但模式的输出值与真实值之间还是存在较大偏差。Xu 等［3］评估了CMIP5 中18 个GCMs 降水数据对中国地区降水变化的模拟效果，发现大多数模式的降水数据偏高，且对降水在时间上变化的模拟能力有限。李振朝等［4］评估了CMIP5中8 个GCMs 对青藏高原地区降水的预估效果，结果表明各模式的年降水预估值均大于实测降水，且预估序列与实测序列间的相关性很小。因此，通过多模式集成综合以提升GCM的模拟精度，成为常用研究方法。许崇海等［5］评估了22 个气候模式对东亚地区气候的模拟能力，表明多模式集合平均的模拟能力比单一模式更优。Santer 等［6］考虑到多模式集合结果通常优于单一模式，且不同模式的模拟能力不同，建议使用加权多模式集合（Multi-Model Ensemble）方法对多模式结果进行综合。王晶［7］利用8个气候模式的回报资料，采用BMA进行多模式集成，比较发现BMA 集成后的回报效果优于单一模式和多模式集合平均。

然而上述研究没有考虑不同模式之间的依赖结构，而模式间的相依关系对模式集成效果是有影响的，通过建立联合分布可以考虑变量之间的相关性。Copula 函数是一种灵活的统计工具，允许不同变量有不同的边缘分布，可用于建立两个或多个随机变量之间的联合概率分布［8］，其中，藤Copula在描述多变量间复杂相关结构时具有更好的灵活性［9，10］。Pham等［11］基于C藤Copula 函数建立了随机蒸散发模型，得到了与降雨一致的日参考蒸散发随机模拟序列。Wang 等［12］基于D 藤Copula 函数，以与当月径流相关的历史径流和气候要素（降雨、温度、蒸发等）构建条件联合分布，较好地模拟了黄河源区月径流。

本文采用C 藤Copula 建立GCM 多模式集成方法。应用泰勒图技术从12 个GCM 模式中挑选6 个较好的模式，构建该6 个模式模拟序列与实测序列的联合分布，推求给定模式数据时实测值的条件分布，据此实现多模式结果的集成。采用相关系数（r）和均方根误差（RMSE）对集成结果的拟合效果进行评价，并将其与单一模式、多模式集合平均进行对比分析。

1 模型与方法

1.1 GCM模式及优选

采用CMIP5 的12 个GCMs 历史模拟实验的降雨模拟数据，模拟数据时段为1961-2005年，12 个GCMs 模式［模式编号］分别为：BCC-CSM1.1［m1］、BCC-CSM-1.1（m）［m2］、CCSM4［m3］、CSIRO-Mk3.6.0［m4］、GFDL-CM3［m5］、GFDL-ESM2G［m6］、IPSL-CM5A-MR［m7］、MIROC5［m8］、MIROC-ESM［m9］、MIROC-ESM-CHEM［m10］、MRI-CGCM3［m11］、NorESM1-M［m12］。

对上述12 个GCMs 模式，采用泰勒图方法［13］评估各模式对实测系列的模拟能力，并从中优选6 个最优的模式。泰勒图方法是将模式模拟系列与实测系列之间的相关系数、各自标准差及均方根误差绘在同一张图上，可以直观地反映模式模拟值对实测值的模拟效果，在气候模式的评估研究中应用广泛［13-15］。本文采用的泰勒图为标准化泰勒图，即将模式模拟系列的标准差、均方根误差除以实测系列的标准差［15］。同时，引入一个综合评价指标Ms［16］来评价模式的综合模拟能力。

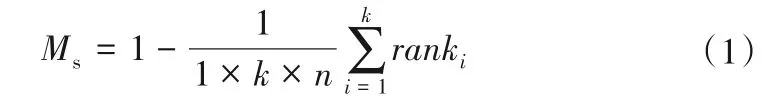
式中：n为选用的GCMs 个数（n=12）；k为评估指标个数（k=3）；ranki为各模式在第i个评估指标下的排名（模拟能力越强排名越靠前，rank值越小）。

显然，模式的综合模拟能力越强，其Ms的值越接近于1，或反之［17］。

1.2 藤Copula

Copula 函数［18，19］是一个定义在［0，1］区间上均匀分布的多维联合分布函数，通过连接多个随机变量任意形式的边缘分布构建联合分布。假设n维随机变量x1，…，xn的联合分布函数为F(x1，x2，…，xn)，则存在一个Copula函数C使得：

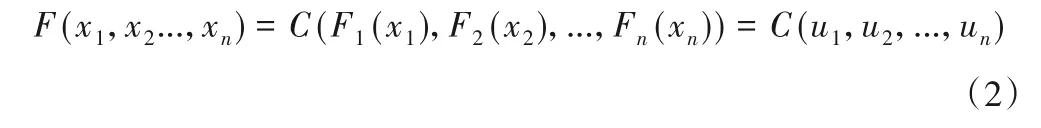
式中：ui=Fi(xi)，i= 1，…，n；Fi(xi)为随机变量xi的边缘分布函数。

假如Fi(xi)，i= 1，…，n都是连续的，那么存在唯一的C。多维联合分布密度函数f(x1，…，xn)可以表示为：

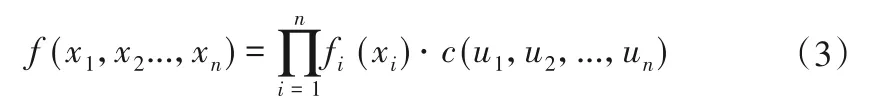
式中：fi(xi)为随机变量xi的边缘密度函数；c(u1，u2，…，un)为Copula密度函数。

当Copula函数绝对连续时，c(u1，u2，…，un)=∂nC(u1，u2，…，un)/∂u1∂u2…∂un。

藤Copula 函数是一种高维Copula 函数，能更好地描述高维变量之间的复杂相依关系。对于高维联合分布，存在很多可能的Pair-Copula 构造方式［20］。为了便于组织Pair-Copula，Bed⁃ford 和Cooke［21］引入了正则藤图形建模工具。一个d维随机变量的正则藤Copula，有d-1 棵树，第k棵树中有d+1-k个节点和d-k条边。其中第一棵树中一个节点代表一个边缘分布，一条边对应一组Pair-Copula，除第一棵树外，其余树节点均为上一棵树的边。

C 藤和D 藤是两种特殊的正则藤，其中C 藤为星型结构，一个中心节点连接了其他所有节点；D藤为平行直线型结构，一个节点最多与两条边连接［20］。藤结构逻辑不同，适用的数据集类型也有所不同。D 藤适合用于描述变量相互独立的数据集，而当数据集含有主导其他变量的关键变量时C藤更合适。

根据Bedford 和Cooke［22］的表述，一个n维C 藤、D 藤Copula的密度函数表达式分别如下：

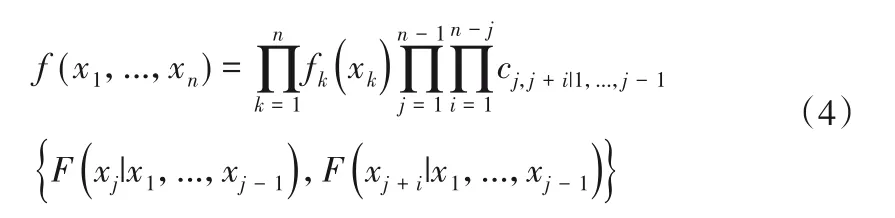
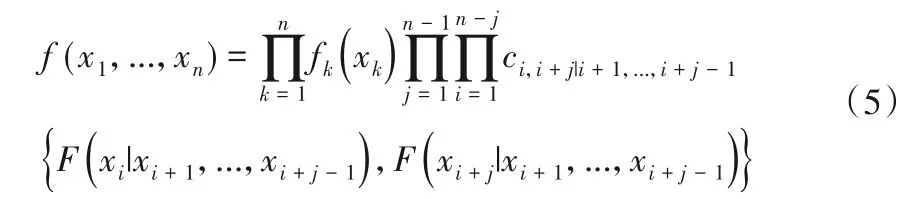
式中：n为随机变量的维数；fk(xk)为边缘密度函数；j为树的棵数；i为树上边的索引；c∙|∙(∙，∙)为藤结构中的二维Copula 的密度函数；F(∙|∙)为条件分布函数。

1.3 条件分布

根据Joe［23］的表述，式（4）和（5）中的条件分布函数可以用如下通用公式表示：

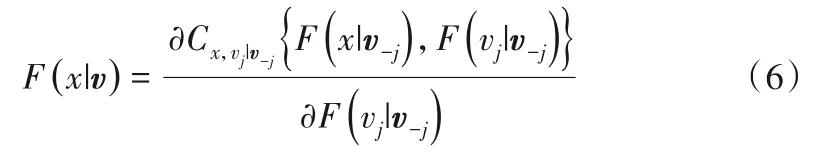
式中：v为一个n维的向量；vj为v中的任意一个变量；v-j为v去除vj后剩余向量；Cx，vj|v-j为二维条件Copula 函数，当v的维数为1时：

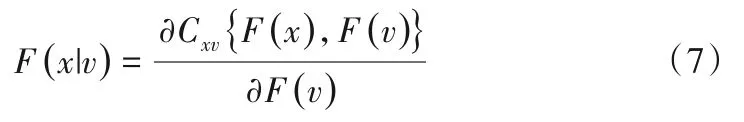
当x和v都服从U[0，1]时，即F(x)=x，F(v)=v，f(x)=f(v)= 1时，可以用h函数表示F(x|v)：

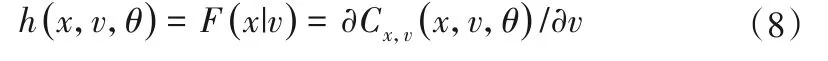
式中：θ为求x，v之间联合分布时Copula函数的参数。

Joe［24］综合介绍了二维单变量的h函数及其反函数。根据式（6），C藤Copula和D 藤Copula的条件分布函数表达式分别为式（9）和（10）：

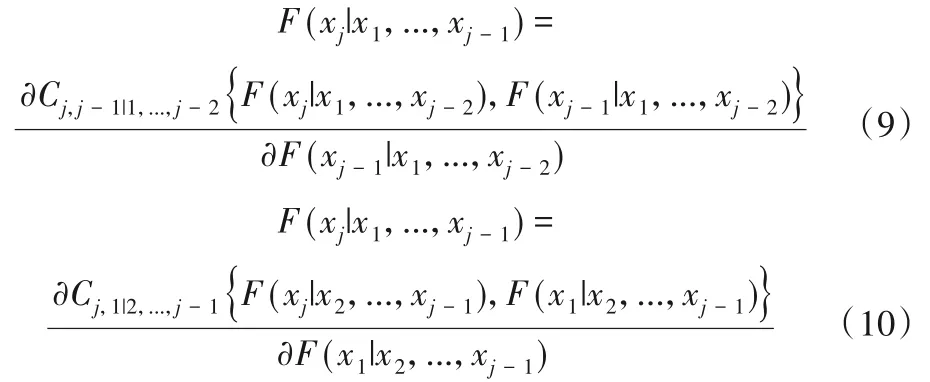
以一个简单的4 维C 藤Copula 条件分布函数为例，根据式（6）～（9），F(x4|x1，x2，x3)可以表示如下：

1.4 随机模拟

根据藤Copula 模型建立的实测序列与模式模拟序列之间的联合分布，可以得到给定模式模拟值时实测值的条件分布函数，并可取条件分布的均值作为综合后的模拟值。假设第m年实测值为Pm，同期d个模式的模拟值分别为Pm1，Pm2，…，Pmd，则实测值可以用条件分布的反函数和随机数得到：

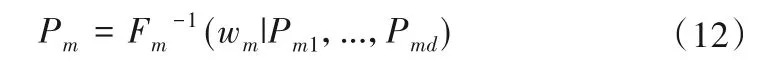
式中：wm为随机数，wm～U[0，1]；Fm-1(⋅|⋅)为第m年给定模式模拟值时实测值的条件分布函数的反函数。

1.5 模拟效果评价

采用Pearson 线性相关系数（r）、均方根误差(RMSE）评价单一模式、多模式集合平均及藤Copula 多模式综合对实测系列的模拟效果。假设xi，i= 1，2，…，n为实测序列，对应的模拟序列为yi，i= 1，2，…，n，则上述两个评价指标的表达式分别为：

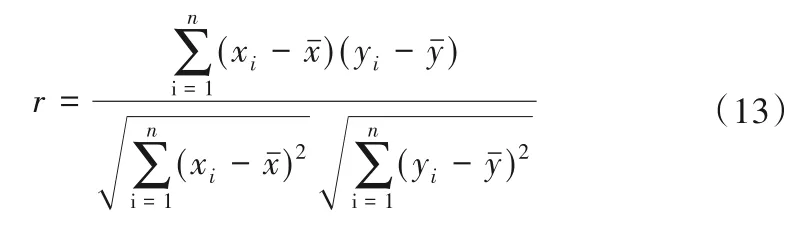
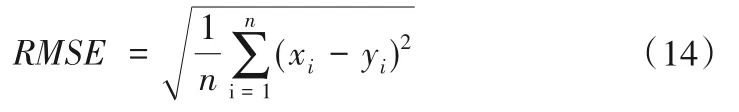
2 实例研究

梧州水文站是珠江流域西江干流的主要控制站，位于111°20′E，23°28′N，控制广西境内85%的集水面积和年径流总量［25］。西江流域位于我国华南沿海，属于热带、亚热带季风气候，降水量的年际变化较大，雨季长且年内分配极不均匀，降水主要集中在4-9月［26］。本次研究以西江梧州站以上流域1961-2005年7月面平均雨量作为研究对象。

2.1 模式优选

构建藤Copula 模型时，随着维数的增加，可能的藤结构个数迅速增加，一个d维随机变量构成的藤Copula，有种可能的C（D）藤，种可能的R 藤［27］。为了避免由于维数过高导致计算效率不高，同时又尽可能多地考虑多个不同模式的信息，通过泰勒图指标综合选用了6个模式。评价原则是：模式模拟值与实测值相关系数越大、均方根误差与实测标准差之比越小、标准差与实测标准差之比越接近1，模拟效果越好［28］。图1给出了12个模式模拟降雨相对于实测值的标准化泰勒图。

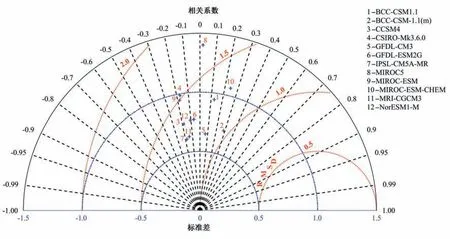
图1 12个GCMs模拟降雨相对于实测值的泰勒图Fig.1 Taylor diagram of simulated precipitation of 12 GCMs relative to observed values

基于泰勒图结果，计算了各模式的综合评价指标Ms。根据表1中的计算结果最终选择了编号为m1，m2，m3，m4，m9，m10的6个GCM模式。

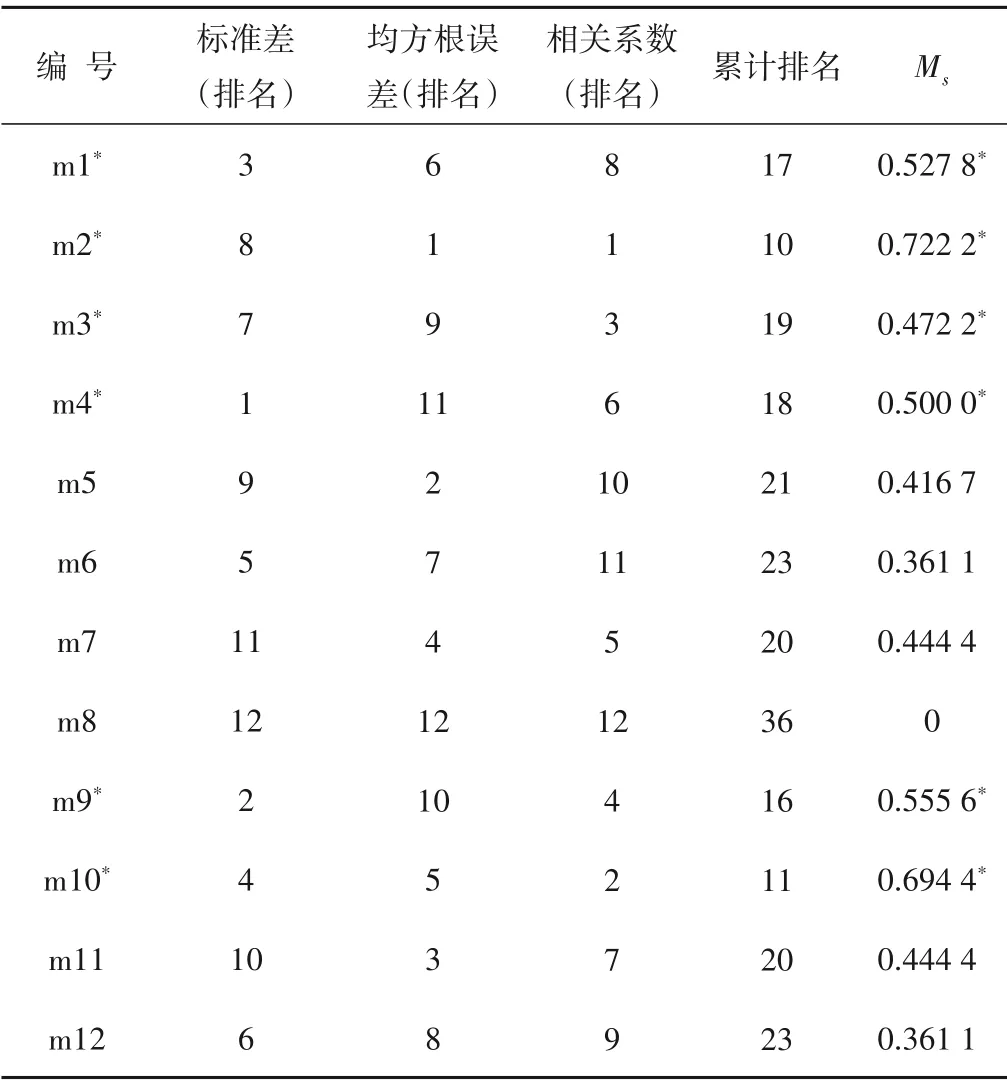
表1 12个GCMs的综合评价指标Tab.1 Comprehensive evaluation index of 12 GCMs

图2给出了1961-2005年实测、6个模式原始模拟系列和多模式平均模拟系列。从图2中可以看出：不同模式模拟值序列差异较大，单个模式的模拟效果不甚理想，而将多个模式进行集合平均处理，又使得模拟序列过于平滑，显著削弱了对极值的估计，不能反映真实月降雨的年际变化情况。

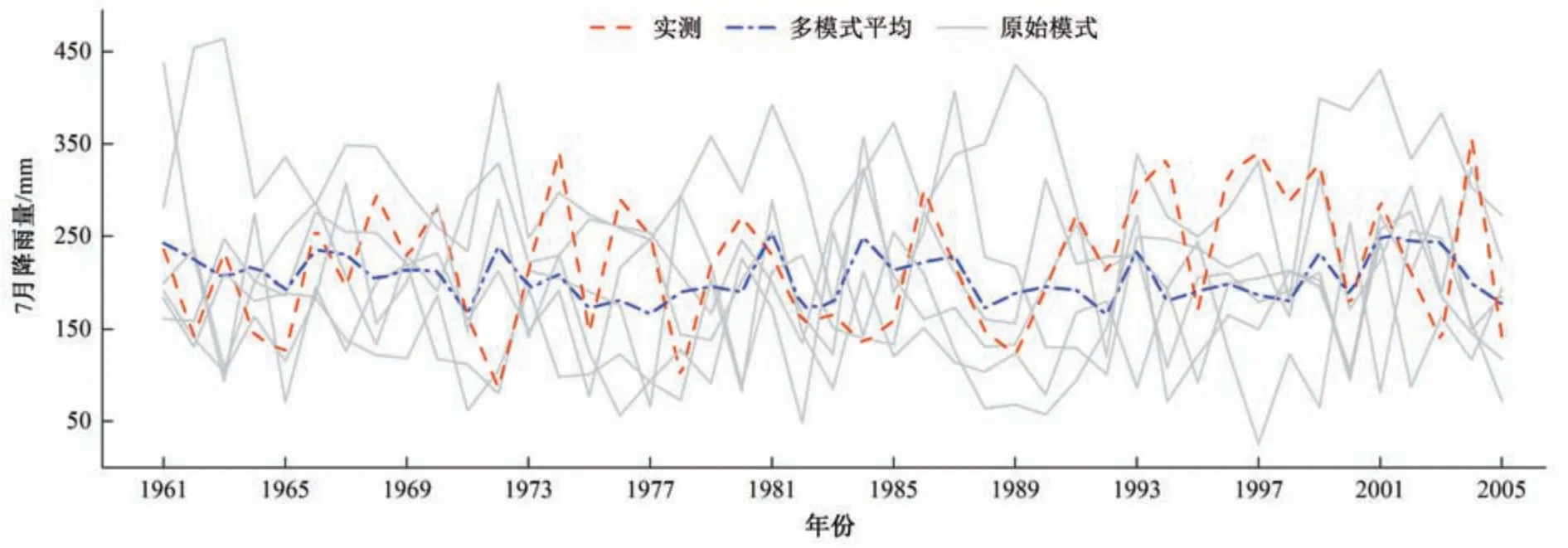
图2 实测降雨和模式模拟降雨时间序列Fig.2 Observed precipitation and model simulated precipitation time series

2.2 最优边缘分布拟合

通过藤Copula 建立联合分布的第一步是选择拟合最优的边缘分布。本次研究的是月降雨数据，选取了常用的GEV、Weibull、Lognormal、Normal和PE3分布函数作为备选边缘分布。采用K-S 检验法在P＝0.05 显著性水平下对各个分布函数的拟合效果进行了分析。以K-S 检验结果中的P值优选分布，当D值比0.05 显著性水平下D的临界值小时，表明通过显著性检验。各模式最终确定的边缘分布及K-S检验结果见表2。

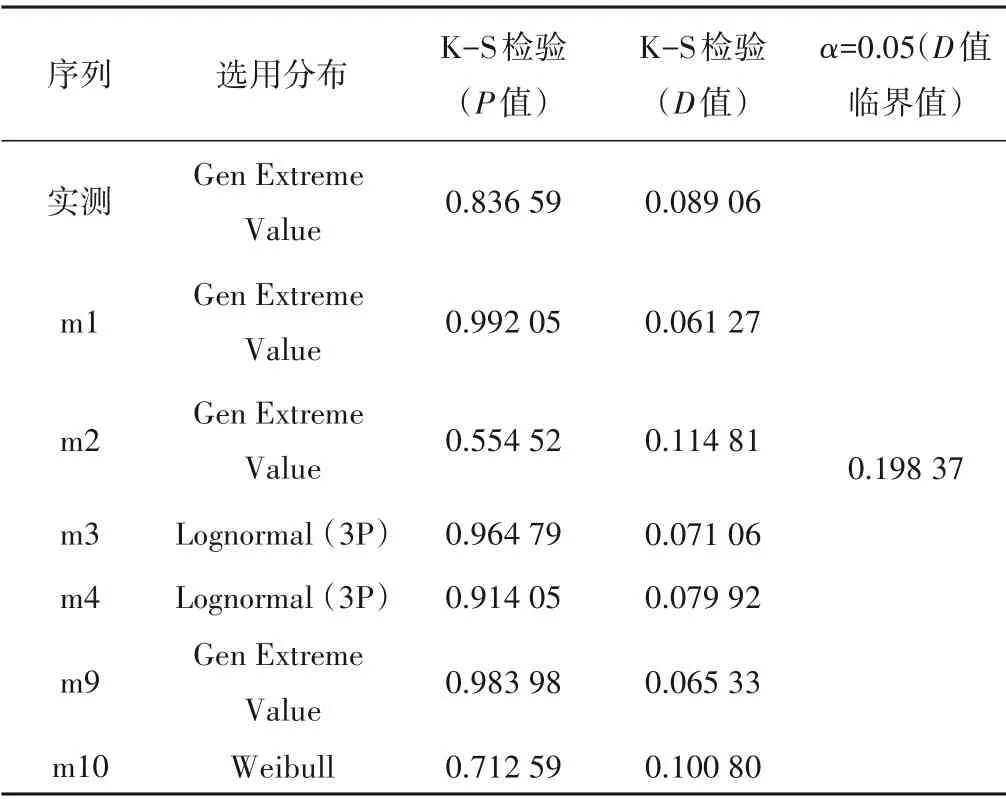
表2 选用边缘分布及K-S检验结果Tab.2 Selection of edge distribution and K-S test results

2.3 建立藤Copula模型

通过藤Copula 建立实测序列与模式模拟序列之间的联合分布，采用在水文领域常用的Archimedean Copula 函数［29］中的Clayton、Gumbel、Frank 型，以及它们的旋转结构作为二维Copu⁃la的选用类型。以AIC准则选出组成藤Copula的最优二维Cop⁃ula 类型，采用极大似然法估计相应参数。以45年模式模拟值和实测值的边缘分布作为输入，分别建立C 藤Copula 和D 藤Copula 模型。依据AIC 准则、BIC 准则和对数似然值（LL）［30］，确定最优拟合的模型，见表3。采用留一交叉验证方法进行效果分析，具体为：对于总共45年的数据资料，每次采用44 a数据构建模型，在构建的模型基础上对剩余1 a 的实测值进行模拟，重复进行45 次，最后将得到的模拟系列与实测系列进行对比分析，评价模拟效果。对于AIC 和BIC 而言，C 藤Copula 的指标结果更小，并且C 藤Copula 的对数似然值更大。为此，本研究采用拟合更优的C藤Copula模型。

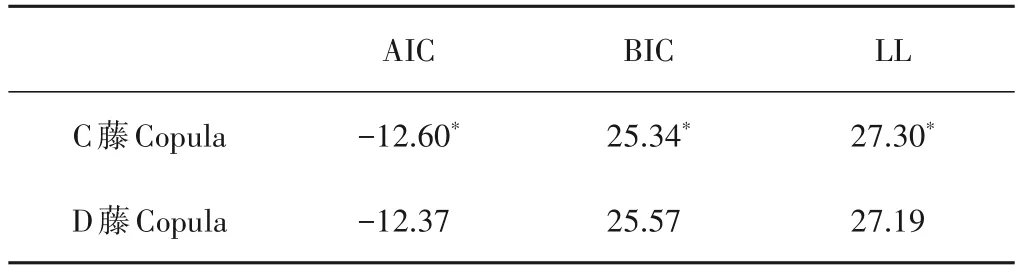
表3 藤Copula拟合优度检验结果Tab.3 Goodness of fit test results of Vine Copula

2.4 随机模拟

根据C 藤Copula 模型构建的实测与模式模拟之间的联合分布，在给定GCMs模拟值的情况下，可以获得实测值的条件分布。由于难以获得条件分布的解析解，为此采用随机模拟的方式进行求解。具体为针对每年的条件分布函数采用马尔科夫链蒙特卡洛方法从条件分布函数中随机抽取1×104个样本，计算1×104个样本的均值并将其作为对应年份的月降雨模拟值，随机模拟系列及其均值模拟序列如图3所示。

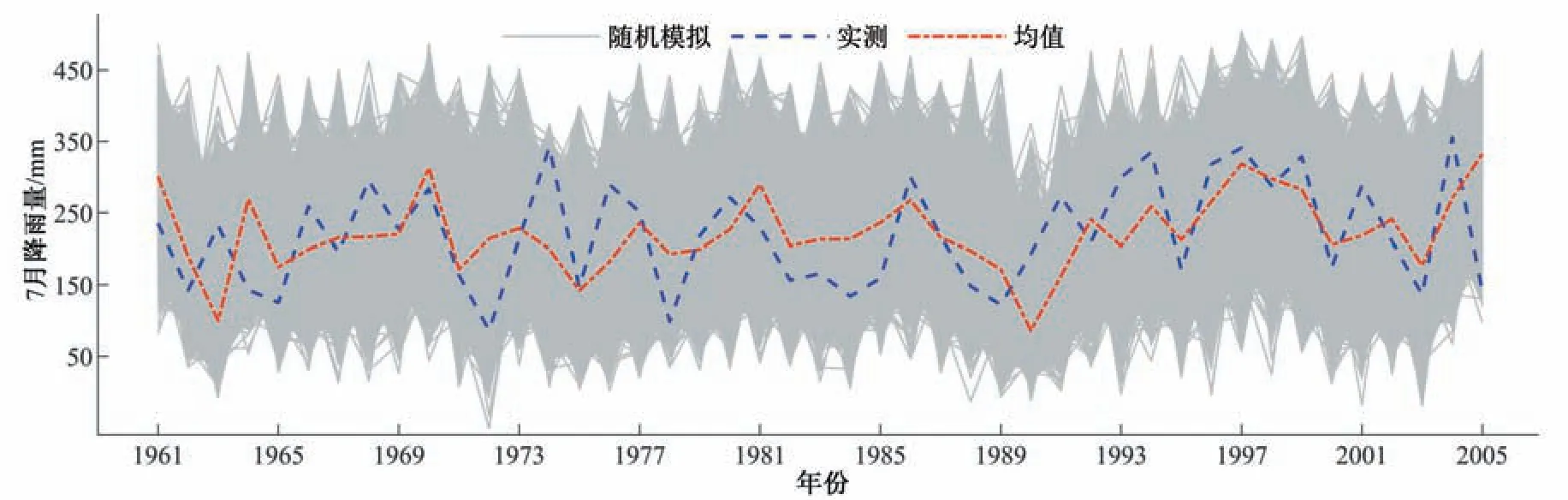
图3 随机模拟值及其均值与实测值时间序列对比图Fig.3 Time series comparison diagram of random simulated values and its mean value with observed values

采用相关系数和均方根误差指标对均值模拟序列的模拟效果进行评价，结果如图4所示。

从图4中可以看出，通过采用C 藤Copula 集成多模式模拟结果得到的均值模拟系列与实测系列间的相关系数比6个模式的都大，从单一模式最大的0.286 提高至0.363；对于均方根误差，由93.487 减少至72.695，均优于多模式集合平均的两个指标评价结果（0.050 和77.903）。由此表明，基于C 藤Copula 的多模式综合方法得到的模拟值比任意单一模式表现更好，且优于多模式集合平均，起到了改善模拟效果的作用。虽然改善的幅度受限于选用的单一模式，但是该方法可以在多模式的基础上提高对月降雨数据的拟合效果。

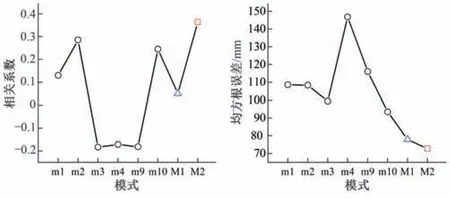
图4 单一模式、多模式集合平均及多模式综合的指标比较Fig.4 Index comparison of single-model，multi-model ensemble mean and multi-model synthesis

3 结 论

本文基于12 个GCMs 模式提供的模拟降雨，采用泰勒图指标优选了6 个模拟能力较好的GCMs，通过藤Copula 构建了CMIP5月降水量多模式综合校正模型，并以西江梧州站以上流域的面雨量为对象进行了示例研究。

（1）基于AIC、BIC 和LL 指标，评估了C 藤Copula 和D 藤Copula 模型的应用效果，结果表明C 藤Copula 的校正效果要优于D藤Copula。

（2）基于相关系数和均方根误差指标，分析了C 藤Copula校正结果与任一原始模式结果的差异。结果表明校正结果优于任一模式的原始结果，也优于多模式的平均结果。此外，通过多模式综合校正后的系列，比多模式平均的系列更能反映真实月降雨的年际变化趋势。

（3）藤Copula 在应用过程中，其结构数目会随着变量维数的增加而急剧增加，会降低计算效率。但若采用的GCMs 模式数目太少，又可能导致数据信息利用不足。为此，在保证校正效果前提下，如何平衡GCM数目选取和藤Copula高效构建有待进一步深入研究。 □