船体曲率板感应加热成形工艺研究

王江超，张楚汉，易斌，周宏，任强，吴泰峰

1 华中科技大学 船舶与海洋工程学院，湖北 武汉 430074

2 江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003

3 中船澄西船舶修造有限公司，江苏 江阴 214433

0 引 言

在船舶结构建造中，常使用曲面分段来确保船舶营运中具有良好的水动力性能，因此，船体曲率板的弯曲成形加工被视为船体钢料加工处理的重要环节。船体曲率板弯曲成形的精度会直接影响船底及舷侧曲面分段的装配和焊接的质量，以及船舶的建造周期和成本。通过加热来实现船体板材弯曲成形的热弯成形是船厂普遍采用的一种方法。以火焰作为热源，通过气体燃烧加热板材表面的热弯成形方法，其弯曲成形的效率较低，且火焰加热的温度分布不易精准控制。同时，因相关过程参数主要依靠经验丰富的技术工人来适时调整，导致了生产效率低下，且无法保证板材的弯曲精度。而感应加热成形虽起步较晚，在船厂的应用还不够普及[1]，但因其特有的优势，在自动化、智能化的先进船舶建造工艺中开始逐步占据重要位置，应用前景更为广阔。该加工方法的加热路径及其工艺参数规划，是当前板材热弯成形工程的应用难点和研究重点。

基于电磁感应加热的热弯成形设备自动化程度较高，可高效地控制热源分布及其产生的弯曲力矩，进而精准地获得需要的面外弯曲变形。Lee 等[2]对比了火焰加热和感应加热这2 种船用钢板加热过程，验证了感应加热应用于钢板弯曲成形的可行性。同时，Lee 等[3]还通过多个线加热实现了船体板材的热弯成形，预测了不同板材厚度、加热速度和线加热热源间距等参数对板材收缩变形及弯曲角度变形的影响。周宏等[4-5]使用热电偶研究了船用钢板在感应加热过程中的温度变化，采用三坐标定位仪测量了冷却后的面外弯曲变形分布和数值，指出在感应加热过程中温度上升会比较迅猛，但在超过居里点以后便会保持不变。日本石川岛播磨重工（Ishikawajima Halima Industry，IHI）与大阪大学联合研发的IHI-α 全自动板材感应加热成形系统，可在自动计算出加热方案后对船体曲率板进行感应加热弯曲成形[6-7]，即首先通过激光测量板材的形状，与目标弯曲形状进行比对，然后规划感应加热过程的工艺参数。该系统可实现板材的自动化翻身操作，能极大地降低人工成本及加工时间。

易斌等[8]针对使用不同感应加热过程得到的帆形板和鞍形板，分别采用热−弹−塑性有限元（thermal elastic plastic finite element，TEP FE）计算和基于固有变形的弹性有限元计算，再现了双曲率板的感应加热弯曲成形过程。Wang 等[9]提出了感应加热弯曲力矩，阐述了感应加热过程工艺参数影响面外弯曲变形的力学机理，发现采用弹性有限元计算可以更高效地预测出感应加热的弯曲变形，且数值结果与测量结果和TEP FE 计算结果相当吻合。Zhang 等[10-11]研究了移动感应加热作用下船体外板的受热及变形现象、热弯成形过程参数对加热热源（最高温度、宽度和深度）和弯曲变形（面内收缩和弯曲角度）的影响。Han 等[12]分析了船体外板线加热成形中，不同热源间距对曲率板成形的影响。Das 等[13]回顾了使用线加热实现船体曲率板成形的研究进展，具体包括了温度场分析、力学响应、加热线生成以及计算分析方法的发展等。Park 等[14]为了解决船体外板自动热弯成形过程中的弯曲过量及失稳等问题，考虑了补偿余量以及初始挠度的影响，并且通过大量建造实例的应用，提高了自动热弯成形系统的精度和效率。

以上文献研究的是船用钢板感应加热弯曲成形的工艺现象，但在建立感应加热过程工艺参数与弯曲变形的内在关系，以及针对目标曲率板的感应加热工艺规划等方面，未见相关的研究。为此，本文拟在8 mm 厚AH36 船用钢板感应加热弯曲成形试验的基础上，首先，通过三坐标定位仪测量面外弯曲变形的分布及其数值；然后，使用高效的TEP FE 计算和基于固有变形的弹性有限元计算，预测面外弯曲变形，并与试验测量数据进行比较；接着，通过高通量的TEP FE 计算，建立感应加热线圈移动速度与弯曲角度之间的内在关系，并提出线性逼近迭代二分法来规划感应加热过程工艺参数；最后，针对单曲率和双曲率的目标板材，提出对应的感应加热轨迹及其工艺参数。

1 基础理论和有限元方法

1.1 电磁感应加热及其热弯成形机理

基于电磁感应生热现象的感应加热工艺，是一种对船用钢板进行热弯成形的新方法。感应加热线圈与电源连接，由电流产生磁场。当感应线圈中出现振荡交变电流时，会在导磁金属周围产生一个交变磁场，从而在导磁金属中产生感应涡流，实现对导磁金属的加热；而当温度上升到船用钢板的居里点时，板材便会失去导磁性，不再产生感应涡流，工件温度也将不再继续上升[15]。

感应加热会促使导磁工件局部温度快速升高，产生热应变，而在周围冷却金属的拘束作用下，便会产生弹−塑性力学响应。当电磁感应加热产生的热应变使材料屈服时，会产生压缩塑性应变；而在冷却降温过程中，又会因周围金属的拘束作用产生拉伸塑性应变。最终，残留的塑性应变会因厚度方向的梯度分布产生弯曲力矩，使感应加热板材出现面外弯曲变形，如式（1）所示。

1.2 热−弹−塑性及弹性有限元分析

基于有限元计算原理，电磁感应加热实现板材热弯成形过程中的热−弹−塑性力学行为可以分为热传递分析和弹−塑性力学分析2 部分[8]。由于温度变化对材料的热物理性能参数影响较大，故首先需要考虑材料的非线性特征，然后应用电磁感应加热的热源模型及设备的输出功率，再现感应加热过程的瞬态温度场分布。以计算的瞬态温度为热载荷，设置力学边界条件，分析板材感应加热作用下的弹−塑性力学响应，进而预测出板材的面外弯曲变形。

由相关理论分析[16]可知，塑性应变及其产生的弯曲力矩是加热板材产生面外弯曲变形的根本原因。如果能计算或者测量得到感应加热对应的弯曲力矩，便可通过弹性有限元计算快速预测出板材的面外弯曲形状及弯曲变形。具体而言，使用壳单元建立所研究板材的有限元网格模型，并设置壳单元的厚度，获得板材弯曲刚度；感应加热生成的横向弯曲力矩即弯曲角度（单位：rad），被施加在加热线两侧，进而再现板材厚度方向因温度梯度不均所产生的弯曲力学响应。

1.3 直线逼近的迭代二分法

从数值分析及计算机图形学的角度来看，任意曲线均可通过直线逼近和表征，且满足工程的精度要求。因此，对于板材的弯曲成形，可基于电磁感应加热的弯曲力矩及弯曲角度，通过直线逼近弯曲目标曲线，即用垂向挠度逼近目标形状的面外弯曲变形，使用迭代二分法来获得电磁感应加热的速度及位置等工艺参数。

假设感应加热板材的长度为a，考虑小变形弯曲情况，且弯曲率板材的曲率均相同，各感应加热之间线性无关。使用二分法在板材长度中心（a/2）处施加感应加热线，并将板材两端固定作为力学边界条件，如图1所示。图中，ACB为感应加热前的初始形状，AC′B为弯曲变形后的形状。若弯曲目标曲线中心的挠度为δc，即CC′长度，则可通过几何关系计算所需要的弯曲角度（弧度制），如式（2）所示；然后再经由弯曲力矩获得感应加热的线能量和感应加热线圈的移动速度等工艺参数[17]。

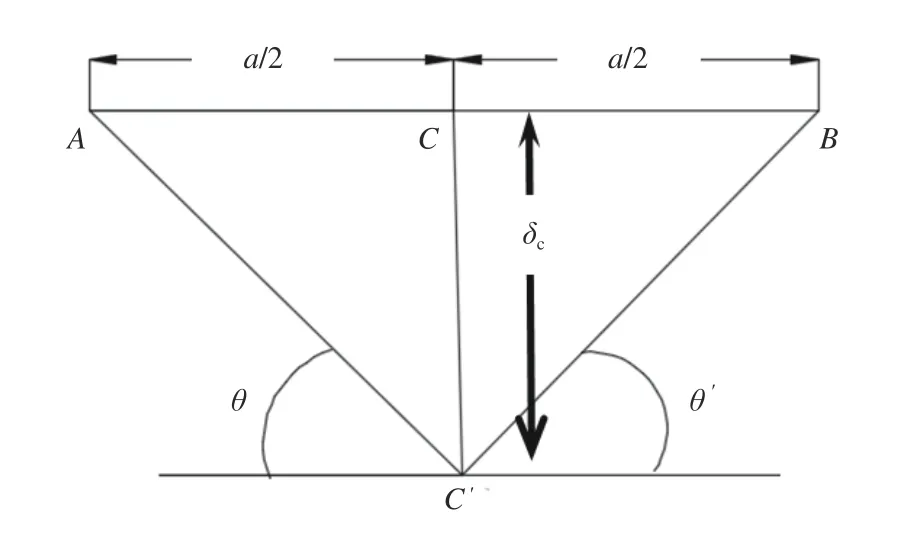
图1 一次二分法的感应加热工艺规划Fig. 1 Processing plan of induction heating with 1st bisection method

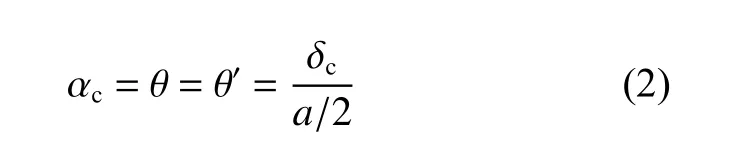
式中：αc为感应加热产生的弯曲角度；θ 和θ'为加热线两侧的水平弯曲角度。

此时，板材长度的两端及中心满足弯曲目标曲线的精度。为确保板材整体弯曲变形的精度，选择a/4 和3a/4 处的计算挠度与目标弯曲变形进行对比。如式（3）所示，若相对误差小于5%，则可认为当前工艺参数能满足船用钢板热弯成形的精度要求，获得与弯曲目标曲线相同的曲率板；若相对误差较大，则需要对当前工艺参数进行优化和完善，依次对板材长度的左半段和右半段进行二分法的二次迭代分析，即除了在板长中心（a/2）处施加感应加热外，还需要在a/4 和3a/4 处施加感应加热，以确保这3 个位置产生的挠度均与弯曲目标曲线一致，如式（4）所示。其中，δ 为加热线位置处弯曲目标形状的垂向挠度。

同理，采用二分法的二次迭代，可以确保a/4，2a/4 和3a/4 处的挠度与弯曲目标形状一致。选择a/8，3a/8，5a/8 和7a/8 处的计算挠度与目标弯曲变形进行对比。若相对误差小于5%，则可认为当前二分法的二次迭代工艺能够满足感应加热的成形要求；若相对误差较大，则需要通过二分法的三次迭代来进行更合适的感应加热工艺规划，如式（5）所示。依次类推，通过二分法的逐步迭代，最终使得规划的感应加热过程工艺参数可以实现船体曲率板的热弯成形，且精度满足工程建造要求。

具体而言，若单曲率板材的长度a=300 mm，目标曲率半径为1.2 m，可通过式（2）得到一次迭代二分法分析时在a/2 处加载的弯曲角度；若a/4和3a/4 处不能满足弯曲精度要求，需再通过式（4）进行二次迭代二分法分析，计算出在a/4，a/2 和3a/4 处 加 载 的 弯 曲 角 度；若a/8，3a/8，5a/8 和7a/8 处不能满足弯曲精度要求，则需再通过式（5）进行三次迭代二分法分析，并检测a/16，3a/16，5a/16，7a/16，9a/16，11a/16，13a/16 和15a/16 处的精度要求；若依然不能满足精度要求，便需再次进行迭代二分法分析，直至满足建造的精度要求，如表1 所示。

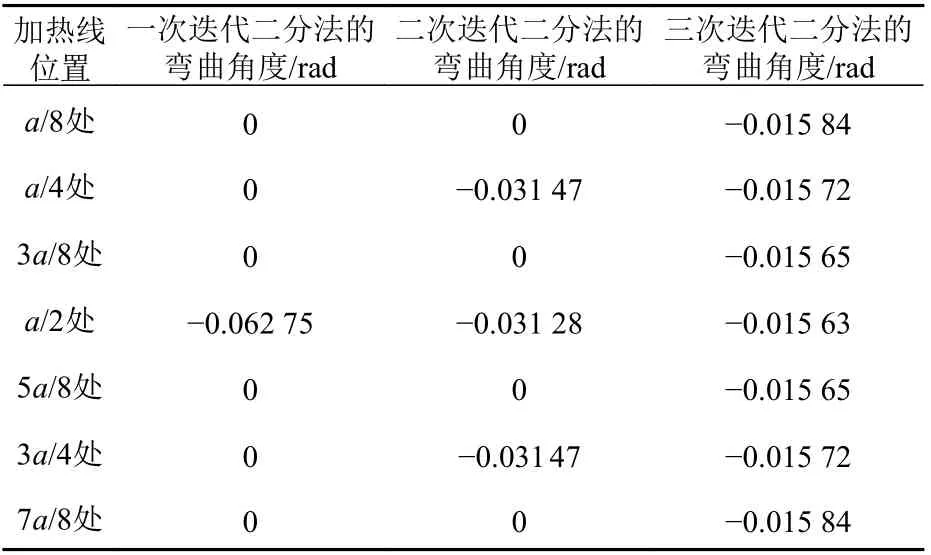
表1 面向目标曲率的线加热位置和弯曲角度Table 1 Positions of line heating and required bending angles for target curvature

2 感 应 加 热 成 形 试 验 及 弯 曲 变 形测量

针对如图2 所示长度a=300 mm，宽度b=200 mm，厚度8 mm 的AH36 船用钢板进行热弯成形试验[4-5]。其中，感应加热设备的功率为25 kW，振荡频率为30～100 kHz，辅助水冷系统功率为12 kW，循环水量12.5 m3/h。感应加热线圈的移动速度为15 mm/s。图3 给出了感应加热的顺序及加热线位置。

图2 感应加热试验设备Fig. 2 Experimental device of induction heating

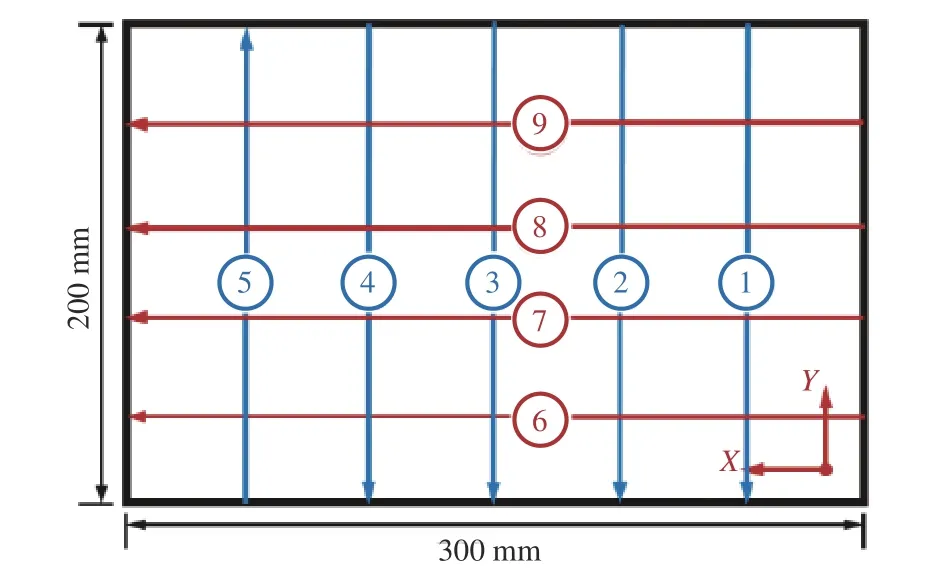
图3 AH36 高强度钢线加热路径Fig. 3 Heating routes on AH36 high tensile strength steel (HTSS)

在感应加热结束、板材冷却至室温后，开始测量面外弯曲变形。首先，对弯曲率板材表面进行除锈清洁，然后，使用高精度的三坐标定位仪（global classic SR 系列，测量精度2 µm）对板材的面外弯曲变形进行测量，如图4 所示。由于在横向和纵向的感应加热及其弯曲变形，使得板材呈现出帆形，即两个方向的弯曲曲率一致。图5所示为计算机图形处理后，测量的AH36 钢板材的面外弯曲变形分布。

3 有限元分析及面外弯曲变形验证

图4 面外弯曲变形测量Fig. 4 Measurement of out-of-plane bending deformation

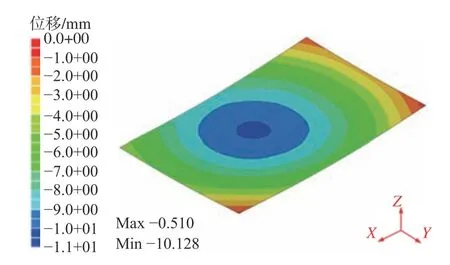
图5 帆形板面外弯曲变形云图Fig. 5 The out-of-plane bending deformation contours of sail-shape plate

基于TEP FE 计算，在对上节所述规格的船用钢板热弯成形进行分析时，需要使用感应加热的热源模型来再现瞬态温度场分布，进而研究热力学响应，并预测冷却后的面外弯曲变形。若获得了热弯成形的弯曲力矩，便可通过弹性有限元计算直接预测最终的面外弯曲变形。下面，分别应用2 种有限元方法预测面外变形，并与试验测量数据进行比较。

3.1 热−弹−塑性有限元分析

使用实体单元对感应加热板材进行有限元建模，如图6 所示，其中节点数为42 517 个，单元数为38 400 个。考虑高强度钢AH36 随温度变化的热物理性能参数，同时使用体热源模型作为感应加热载荷对温度场进行分析，并以温度为热载荷进行逐步加载，施加如图6 所示的刚体位移边界条件，预测的面外弯曲变形如图7 所示。

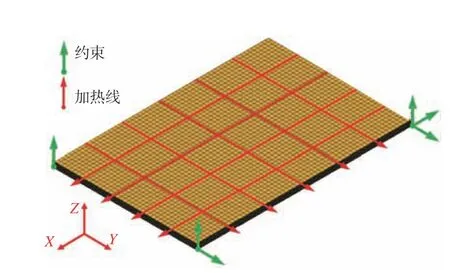
图6 AH36 试板的有限元模型Fig. 6 Finite element model of AH36 specimen

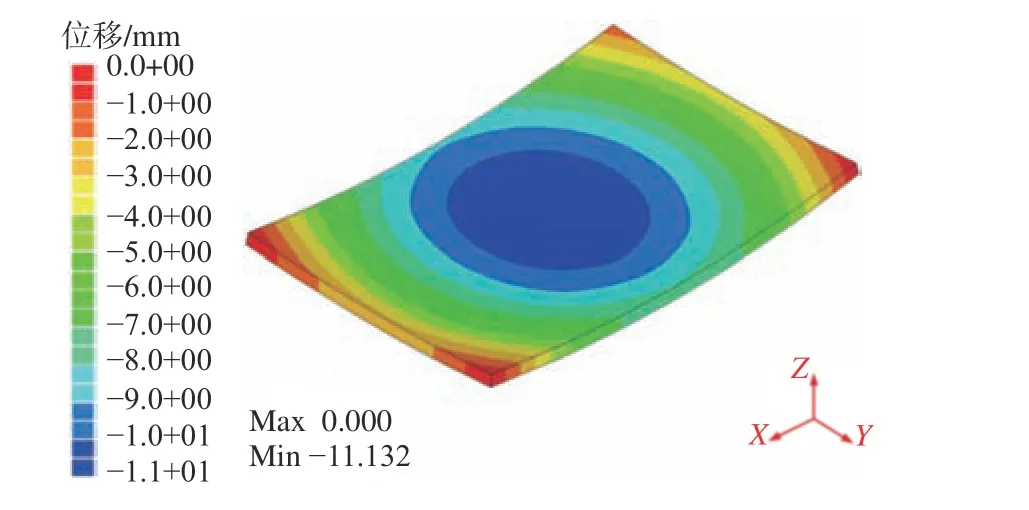
图7 TEP FE 计算的面外弯曲变形云图Fig. 7 The computed out-of-plane bending deformation contours by TEP FE method

3.2 弹性有限元分析

基于上述TEP FE 计算结果，可以获得每个单元沿长度方向（X轴）和宽度方向（Y轴）的塑性应变[9]。由式（1），对垂直感应加热方向的残余塑性应变进行积分，获得对应的弯曲力矩。由式（6），可将感应加热的弯曲力矩转化为弯曲角度，即感应加热的固有弯曲[18]。当感应加热线足够长时，感应加热过程趋于稳定，垂直于感应加热方向的各横截面上的塑性应变分布相同，数值大小也相同。因此，忽略感应加热起始和结束端的影响，仅关注感应加热的稳定区，通过横截面塑性应变积分得到的弯曲力矩（弯曲角度）其数值也相同。此时，获得的弯曲力矩（弯曲角度）可以称为固有弯曲力矩（固有弯曲角度），如表2 所示。

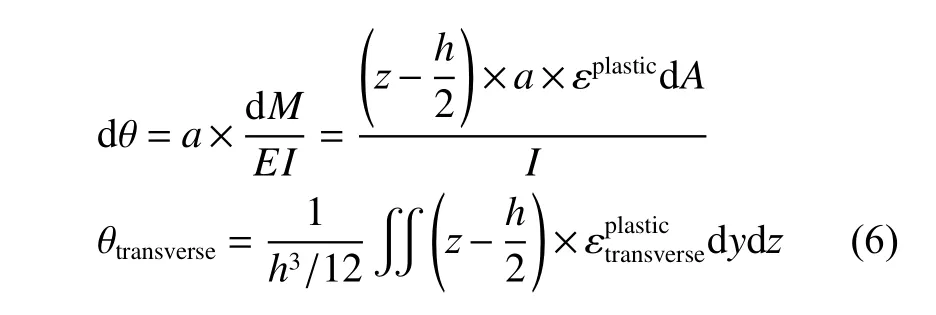
式中：M为弯曲力矩；I为惯性矩。

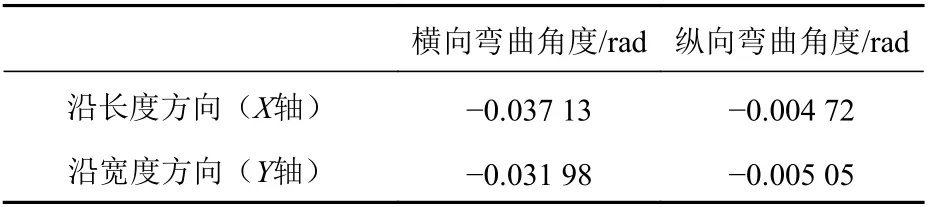
表2 感应加热的固有变形数值Table 2 Evaluated inherent deformation of induction heating

同理，使用壳单元对感应加热板材进行弹性有限元建模，如图8 所示，其中节点数2 501 个，单元数2 400 个，与试验过程相一致，沿长度方向有4 条加热线，沿宽度方向有5 条加热线。以图8所示的刚体位移作为边界条件，以感应加热的固有弯曲作为载荷，进行弹性有限元计算，预测出感应加热的面外弯曲变形如图9 所示。

3.3 计算结果对比

图8 AH36 试板的壳单元有限元模型Fig. 8 Shell element finite element model of AH36 specimen

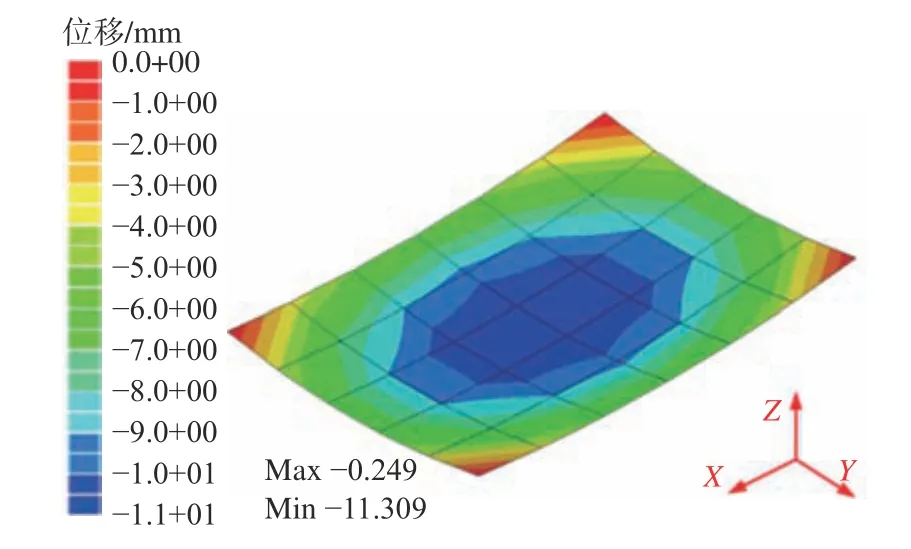
图9 弹性有限元计算的面外弯曲变形云图Fig. 9 The computed out-of-plane bending deformation contours by elastic FE method

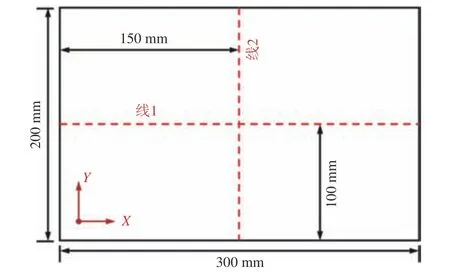
图10 面外弯曲变形对比点位置示意图Fig. 10 Schematic diagram of points location for out-of-plane bending deformation

为了验证有限元计算的准确性，选取图10 所示线1（长度方向）和线2（宽度方向）上的点与测量结果进行对比。图11 所示为AH36 感应加热板材面外弯曲变形的对比。由图可知，预测的线1和线2 上各点的面外弯曲变形与测量数据基本吻合，且趋势一致；同时，线1 和线2 的弯曲方向一致，即AH36 试板在感应加热后呈现帆形弯曲变形。

由上可见，TEP FE 分析均能较为精确地预测出试板感应加热的面外弯曲变形；相对于TEP FE 分析（耗时4 140 min），弹性有限元分析模型较为简单，计算所消耗的资源更少，时间更短（耗时4 min）。

4 感应加热数据库建立及回归分析

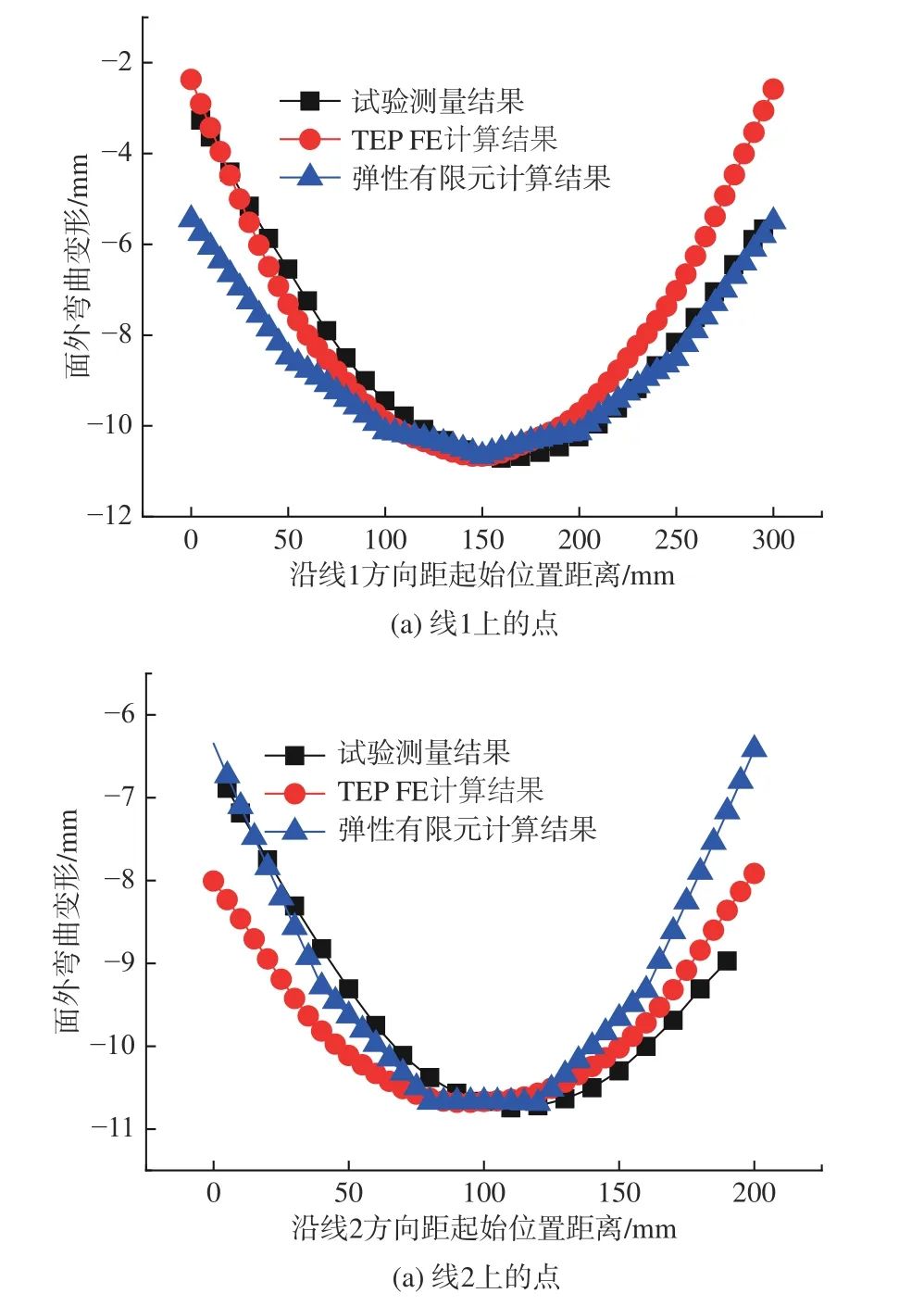
图11 3 种方法面外弯曲变形结果对比Fig. 11 Comparison of out-of-plane bending deformation results obtained by the three methods

上述TEP FE 计算不但可以再现感应加热的热力学耦合过程，而且预测的面外弯曲变形结果与试验测量结果基本吻合。考虑到试验过程及成本，可通过高通量的TEP FE 计算，即使用OpenMP并行计算技术来提升服务器CPU 线程的使用效率，实现计算和存储数据的快速处理，以及“算得多”和“算得快”的功能[19]；分析不同的感应加热线圈移动速度下产生的面外弯曲变形，以及弯曲力矩和弯曲角度，建立感应加热数据库。同时，对分析的样本点（不同的感应加热线圈移动速度及其产生的面外弯曲角度）进行回归分析，得到面外弯曲角度与感应线圈移动速度之间的关系，如图12 所示。

5 感应加热工艺规划及验证

基于上述感应加热弯曲角度与线圈移动速度间的内在关系，针对长300 mm，宽200 mm，厚8 mm 的AH36 钢板（弹性模量E为210 GP，泊松比为0.3），验证迭代二分法在感应加热板材成形工艺规划中的可行性。

5.1 单曲率板材弯曲工艺及对比验证

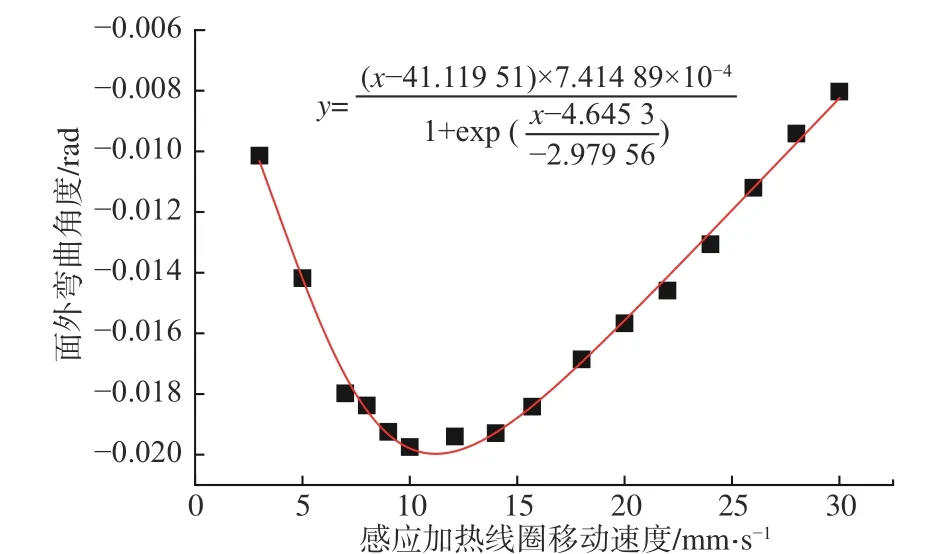
图12 感应加热线圈移动速度与面外弯曲角度的关系Fig. 12 Relationship between moving speed of induction heating coil and out-of-plane bending angular

若沿长度方向（300 mm）单曲率板面外弯曲的目标曲率半径为1.2 m，分析规划的感应加热弯曲角度如表3 所示。同时，基于感应加热数据库，可以得到感应加热弯曲角度对应的感应线圈（热源）移动速度（因设备的功率不变，热源移动速度将直接决定加热的热输入大小），如表3 所示。

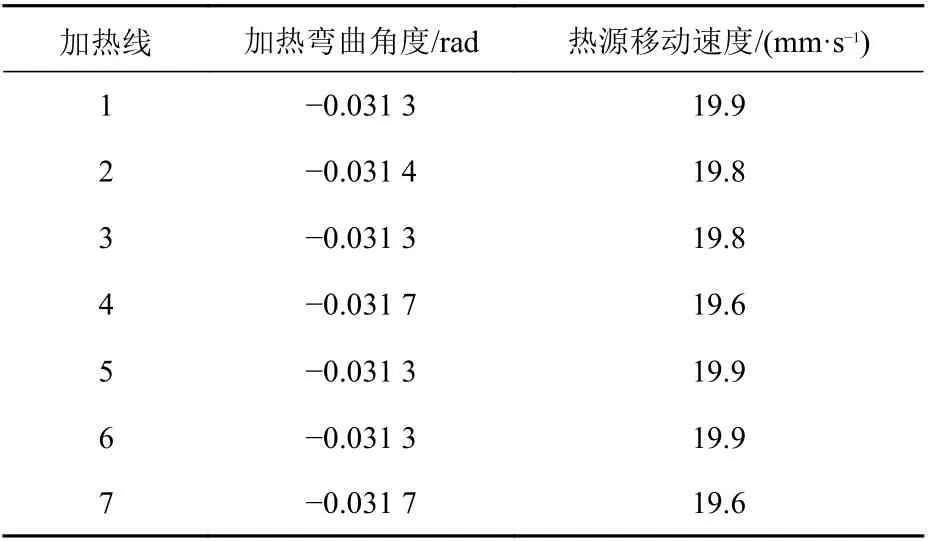
表3 单曲率板热弯成形工艺参数Table 3 Process parameters of plate thermal bending forming with single curvature

以感应加热的弯曲力矩，即弯曲角度为载荷进行弹性有限元分析，预测产生的面外弯曲变形，并与目标弯曲形状进行对比。使用图13 所示的壳单元有限元模型(其中，节点数4 961 个，单元数76 800 个)，应用三次迭代二分法规划的工艺参数，即施加的7 条感应加热路径，如图13 所示。

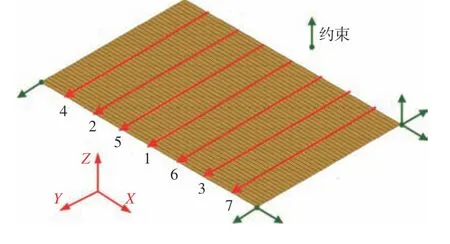
图13 单曲率弯板壳单元模型Fig. 13 Shell element model for plate bending with single curvature

图14 单曲率弯板实体单元模型Fig. 14 Solid element model for plate bending with single curvature

考虑感应加热的体热源模型和对应的线圈移动速度，进行TEP FE 分析和验证。采用实体单元建立的有限元模型，其网格划分和加热线分布情况如图14 所示。其中，节点84 337个，实体单元76 800 个，总计7 条加热路径，与三次迭代二分法的加热工艺参数一致。沿着板材长度方向（300 mm），取TEP FE 计算的面外弯曲变形，并与弹性有限元计算结果和目标弯曲形状进行对比，结果如图15 所示。由图可以看出，对于施加线性逼近的迭代二分法规划得到的工艺参数，通过2 种有限元计算得到的面外弯曲变形与目标弯曲形状呈现高度吻合的现象。同时，对于工程问题，基于弯曲力矩的弹性有限元分析，可以快速校验迭代二分法规划的感应加热路径及工艺参数，具有高效便捷且精度可靠的特点。

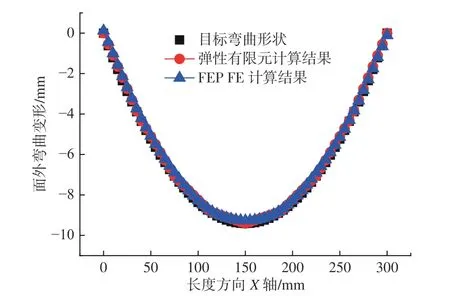
图15 基于工艺规划的单曲率板计算结果与目标弯曲形状对比Fig. 15 Comparison between computed results and target plate bending deformation with single curvature based on processing plan

5.2 双曲率帆形板弯曲工艺及对比验证

本节将研究板材通过热弯得到双曲率的帆形板。其中，板在长度和宽度方向的曲率半径分别为1.0 和0.8 m。基于迭代二分法规划获得的感应加热弯曲角度及其对应的感应加热线圈（热源）移动速度如表4 所示。

同理，使用图16 所示壳单元有限元模型（其中，节点数10 004，单元数9 600），应用迭代二分法规划的线加热位置及其工艺参数，在横、纵向方向分别施加7 条加热路径。以表4中感应加热弯曲力矩，即弯曲角度为载荷进行弹性有限元分析，预测出面外弯曲变形如图17 所示。

图18 所示为实体单元模型。其中，节点166 617个，实体单元153 600 个，在纵、横向方向分别施加有7 条加热路径，所采用的感应加热线圈移动速度如表4 所示。使用体热源模型来考虑感应加热板材成形的热力学响应，进行TEP FE 分析，得到的面外弯曲变形如图19 所示。

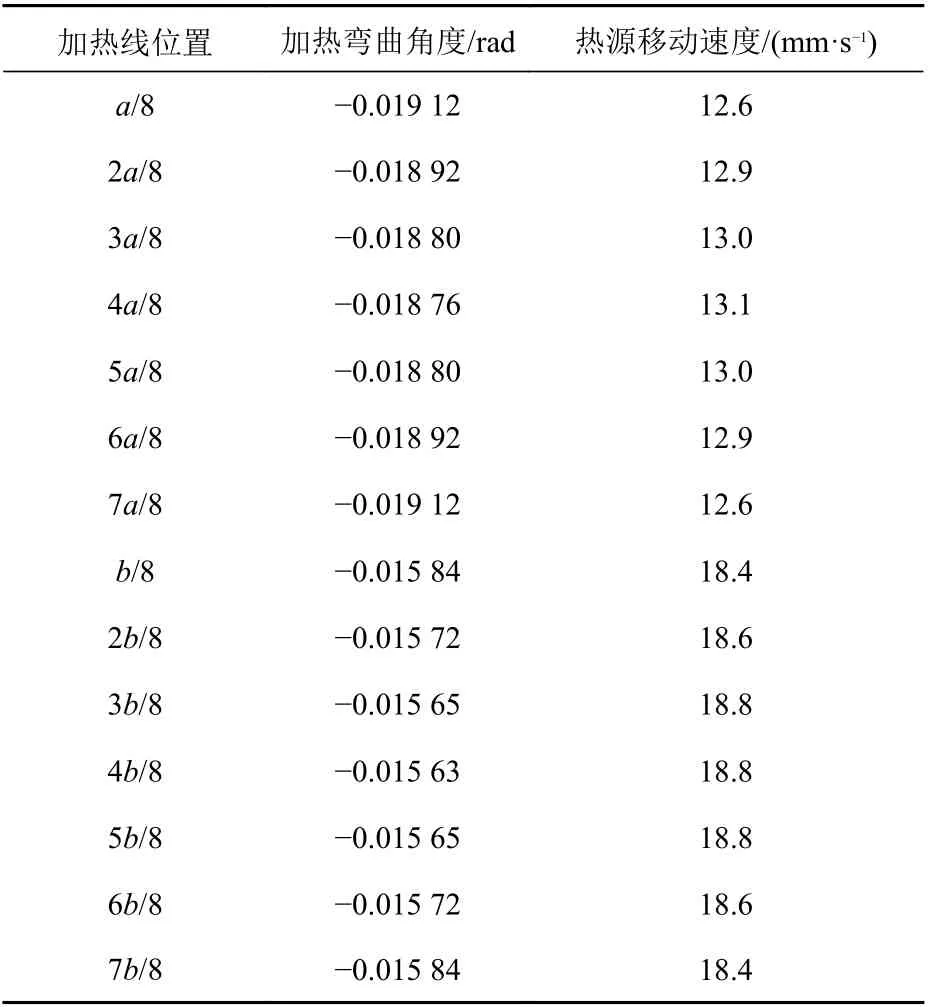
表4 双曲率帆形板热弯成形工艺参数Table 4 Processing parameters of thermal bending forming of sail-shape plate with double curvature

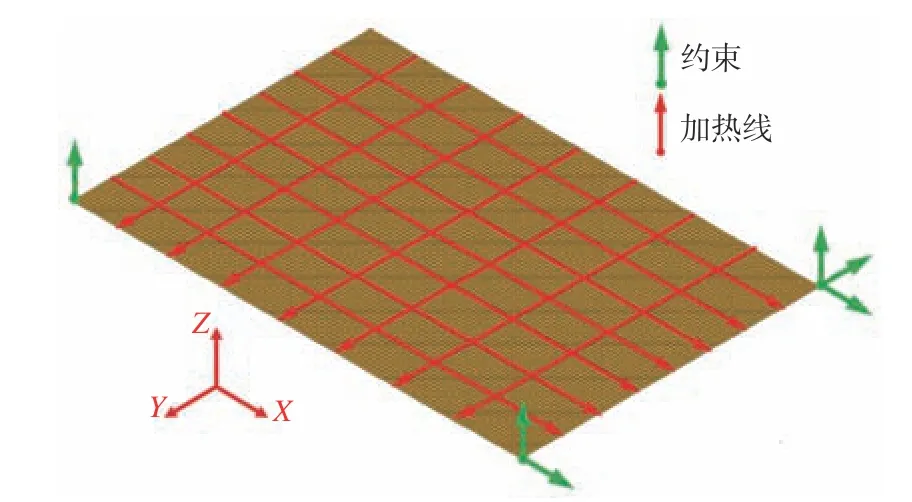
图16 双曲率帆形板壳单元模型Fig. 16 Shell element model for sail-shape plate bending with double curvature

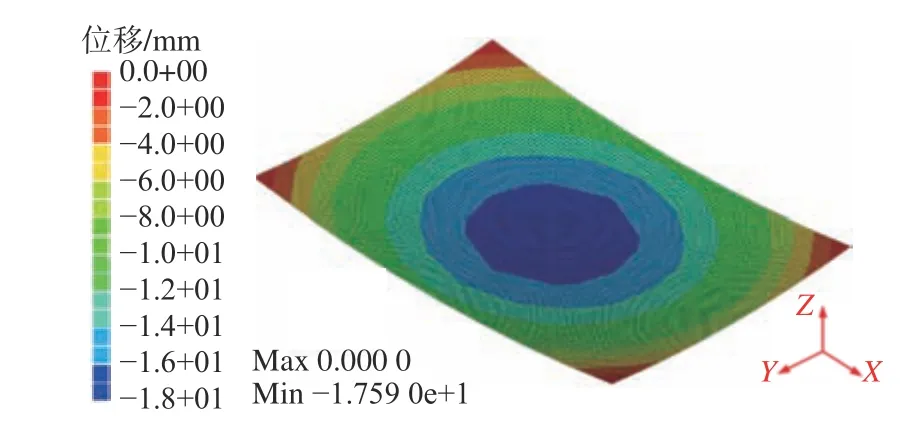
图17 弹性有限元计算的帆形板弯曲变形云图Fig. 17 The computed out-of-plane bending deformation contours of sail-shape plate by elastic FE method

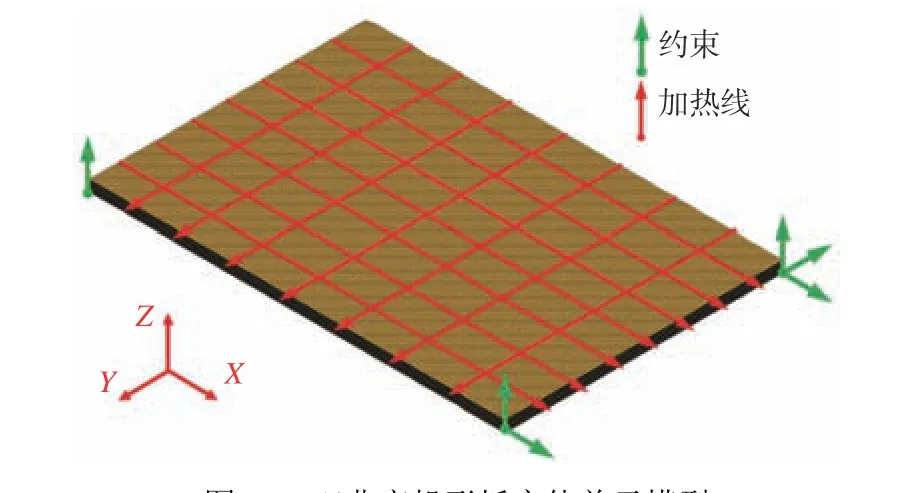
图18 双曲率帆形板实体单元模型Fig. 18 Solid element model of sail-shape plate bending with double curvature

图19 TEP FE 计算的帆形板弯曲变形云图Fig. 19 The computed out-of-plane bending deformation contours of sail-shape plate by TEP FE method

为了进一步验证迭代二分法在双曲率曲率板成形中的应用效果，分别对比了长度和宽度方向上的面外弯曲变形，如图20 所示。其中，TEP FE 计算的面外弯曲变形与弹性有限元计算结果和目标弯曲形状数值基本吻合。具体而言，宽度和长度方向面外弯曲变形的最大相对误差分别为4.9%和14.5%。

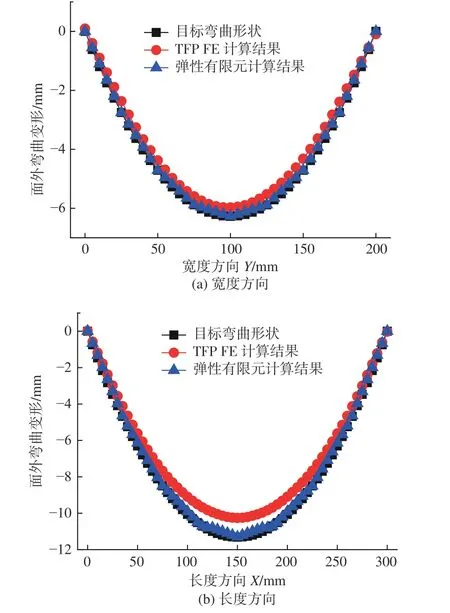
图20 基于工艺规划的双曲率板计算结果与目标弯曲形状的对比Fig. 20 Comparison between computed results and target plate bending deformation with double curvature based on processing plan

由上文可见，线性逼近迭代二分法可针对不同的船体曲率板，高效且较为准确地规划出感应加热的位置和对应的工艺参数；因双曲率板材成形时，长度方向和宽度方向的感应加热过程会产生耦合效应，故其热弯成形工艺还需进一步予以研究。

6 结 论

本文基于船体曲率板感应加热弯曲试验、有限元计算分析以及对线性逼近迭代二分法的应用等研究，全面且系统地构建了船体板材热弯成形工艺研究框架，主要得到以下结论：

1） 感应加热可以实现船用钢板的热弯成形，三坐标定位仪能够精确地测量出面外弯曲变形的分布及数值。

2） 通过感应加热弯曲力矩阐述了板材弯曲成形的机理，同时采用横断面残余压缩塑性应变积分的方式获得了其精确数值。

3） 采用高效的TEP FE 分析和基于弯曲力矩的弹性有限元分析，均可再现双曲率板热弯成形的力学响应，且预测结果与试验测量数据高度吻合。

4） 针对目标船体曲板，提出线性逼近迭代二分法来规划感应加热过程的工艺参数，通过单曲率和双曲率帆形板分析，验证了该过程工艺参数的准确性。