典型舱内爆炸载荷对加筋板的毁伤特性

焦立启，张权，李茂，张磊，张春辉

1 海军研究院，北京 100161

2 中国核动力研究设计院核反应堆系统设计技术重点实验室，四川 成都 610213

0 引 言

随着反舰武器的发展，半穿甲型反舰导弹成为了破坏水面舰艇船体结构的主要进攻手段。战斗部穿过舱室外板在舱内爆炸后，武器的毁伤威力显著增强，不仅包括爆炸产生的冲击波载荷对舰艇结构的毁伤，也有战斗部爆炸后所产生准静态气压对舰艇舱室结构的进一步损伤。通过对比舱内爆炸实验和空中爆炸载荷作用下加筋板的毁伤变形，可知舱内爆炸载荷与空中自由场爆炸载荷差别较大。研究舱内爆炸冲击波载荷与准静态气压联合作用对舰艇结构防护和毁伤评估具有重要意义。

对舱内爆炸载荷特性的研究，多以舱内爆炸实验和舱内爆炸数值仿真为主。Sauvan 等[1]采用在爆源周围添加板架结构的办法模拟舱内爆炸中反射冲击波的耦合作用，研究了舱内爆炸反射冲击波载荷的产生。Baker[2]根据舱室内爆冲击波超压峰值大、作用时间短、存在多次反射的特点，开展了一系列实验和理论研究，提出了著名的冲击波三波等效法。侯海量等[3]使用典型舱室进行了舱内爆炸模型的实验研究，研究表明，由于舰艇结构的影响，舱内爆炸下舱室板架结构所承受的冲击载荷除壁面反射冲击波外，在舱室角隅部位还有强度远大于壁面反射冲击波的汇聚冲击波，以及这些冲击波的多次反复作用。孔祥韶等[4]进行了多层防护结构舱内爆炸实验研究，通过对实验数据的分析，表明在爆炸载荷作用下，水舱内板的动响应出现了“二次加载”现象。樊壮卿等[5]利用有限元软件ANSYS/LS-DYNA 进行典型舱内爆炸仿真，分析了舱内爆炸载荷的传播特性，提出舱内由于冲击波反射作用，形成了准静态压力区。劳氏军标[6]指出，准静态气压峰值和装药与舱室体积之比密切相关。张玉磊等[7]和金朋刚等[8]通过实验，得到了装药与舱室体积之比对准静态气压峰值起决定性影响的结论，并利用实验数据拟合出了计算准静态压力的经验公式。从以上研究可以得出，在不计破片载荷的情况下，舱内爆炸载荷主要包括冲击波载荷和准静态气压载荷。

也有一些学者对冲击波及准静态气压作用下加筋板的动态响应与毁伤模式进行了研究。鄢顺伟等[9]通过对不同板厚舱壁在反舰导弹内爆下的毁伤情况进行数值模拟，总结出内爆冲击波是毁伤的主要因素。姚术健等[10]对内爆载荷作用下钢箱结构的变形规律进行了实验研究，结果表明箱型结构内部爆炸能够造成比空爆更严重的破坏效果，壁板中心变形达到最大值后，板的变形会产生一定量的振荡回缩。李伟等[11]针对战斗部舱内爆炸对舱室结构的毁伤进行实验，分析了舱内爆炸环境下舱室板架结构的典型破损模式，结果显示在战斗部内爆载荷作用下舱室结构的整体变形是以冲击波破坏为主。杨超等[12]开展了固支加筋板在矩形、三角形和指数这3 种爆炸冲击载荷下的数值仿真，得出在3 种载荷强度相等的条件下，结构前期的动态响应基本相同，对于结构整体毁伤，矩形的脉冲载荷破坏最严重，而指数形式脉冲载荷的毁伤能力最弱。陈鹏宇等[13]使用无量纲相对刚度和挠度比界定了爆炸冲击波载荷下加筋板变形与吸能的关系，研究结果可为舰船结构抗爆和泄爆提供参考。焦立启等[14]使用无量纲数描述单向加筋板在冲击波作用下的破损模式，给出了不同破坏模式下无量纲数的取值范围。

英国劳氏军标[6]在其“内部爆炸”一章中规定：如果武器具有足够的当量能通过冲击载荷造成结构损伤，那么结构也会在基于准静态气压水平的动载荷评估中损伤。其指出，在舰船舱室内部发生爆炸时，冲击波与准静态气压载荷对结构毁伤都有贡献。

通过对以上研究内容的总结，发现目前针对爆炸冲击波和准静态气压这2 种载荷联合作用下加筋板的毁伤研究较少。本文将主要模拟载荷冲量相等和载荷峰值相等时固支单向加筋板的变形特性，根据典型舱内爆炸载荷，即爆炸冲击波载荷和准静态气压载荷的联合作用形式，将2 种载荷分开，开展2 种载荷单独作用和联合作用下加筋板变形特性的仿真研究。

1 数值模型

为研究典型舱内爆炸载荷对舱室板架结构的变形特性，选取了舰艇典型舱室板架结构单向加筋板，其尺寸结构如图1 所示。然后采用LS-DYNA非线性动力有限元分析程序进行数值仿真计算，建立目标板架模型如图2 所示。

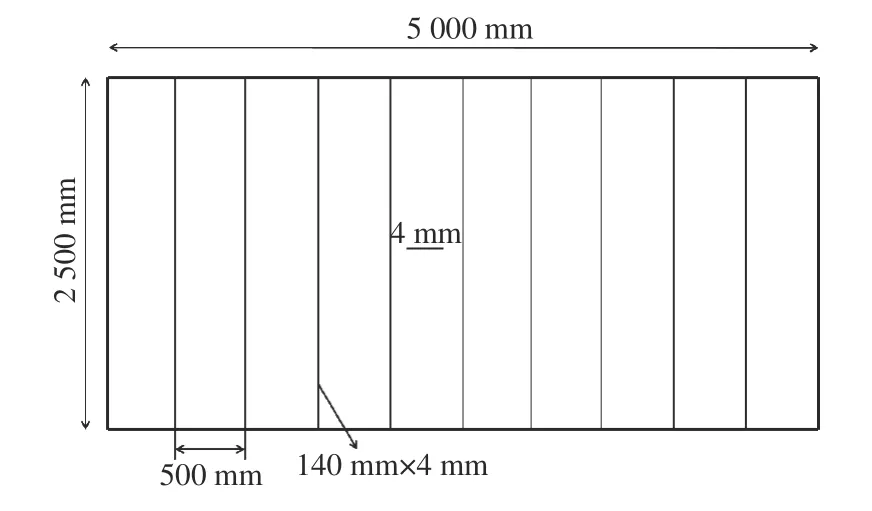
图1 加筋板尺寸结构图Fig. 1 Dimension structure of stiffened plate

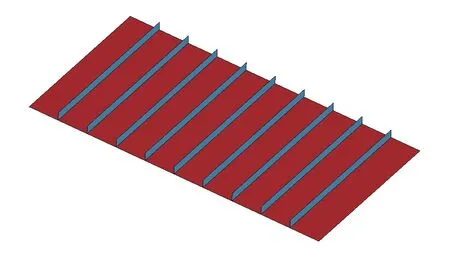
图2 加筋板模型图Fig. 2 Model drawing of stiffened plate

对四边形壳单元建模，模型长l=5 000 mm，宽d=2 500 mm，加强筋高h=140 mm，加强筋间距a=500 mm，板厚H=4 mm，网格尺寸均为15 mm×15 mm。

面板和加筋结构材料均采用双线性弹塑性本构模型Plastic_Kinematic，其应变率效应由Cowper-Symonds 材料模型描述：

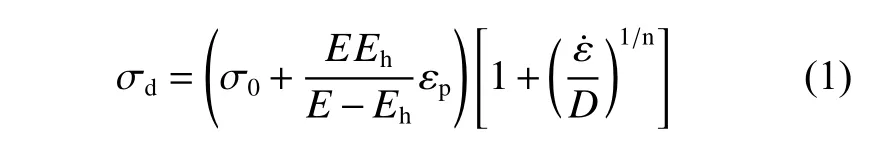
式中 ：σd为动态屈服强度；σ0为静态屈服强度；E为弹 性模量；Eh为硬化模 量； εp为 有效塑性应变； ε˙为等效塑性应变率；D，n为常数，对于低碳钢，通常取D=40.4 s−1，n=5。本文使用的材料为Q235低碳钢，密度ρ =7 800 kg/m3，静态屈服强度σ0=235 MPa，材料失效模型采用最大等效塑性应变失效准则，失效应变取0.3。

2 数值模拟方法实验验证

美军标准UFC-3-340-02[15]将密闭空间内的载荷等效为了2 个部分，第1 部分为无升压时间的三角形冲击波压力脉冲，第2 部分为峰值压力较小、脉宽较长的准静态压力。由此，可将舱内爆炸载荷等效为冲击波载荷和准静态气压载荷。载荷形式如图3 所示。

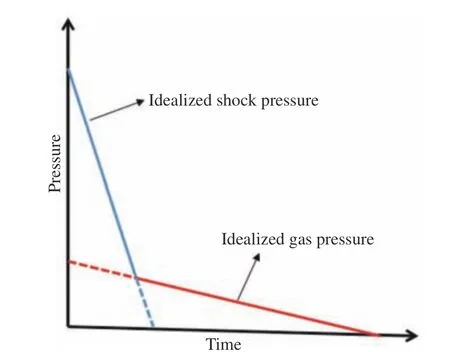
图3 美军标准UFC-3-340-02 中的舱内爆炸载荷模式[15]Fig. 3 The mode of explosion load in the cabin of USA standard UFC-3-340-02[15]

准静态气压与冲击波相比只是峰值小，脉宽大，但就时间量级来说，其仍属于冲击性质的三角形载荷。按照上述仿真方法以及材料参数设置进行爆炸冲击载荷下加筋板的毁伤数值模拟，验证仿真软件对于冲击波载荷下结构响应计算的准确性，即可证明仿真方法对于三角形载荷计算的适用性。采用文献[16]中的空爆实验进行验证。试件尺寸为500 mm× 500 mm，装药为400 g TNT柱状药，尺寸为131.2 mm×50.2 mm，爆距148 mm。所建模型壳单元网格尺寸为5 mm×5 mm，边界条件为四周固支，采用流固耦合算法同时加载模拟炸药。与实验结果[16]进行对比，结果如图4 和图5所示。

图4 实验与仿真的变形模式对比Fig. 4 Comparison of test and simulation deformation modes

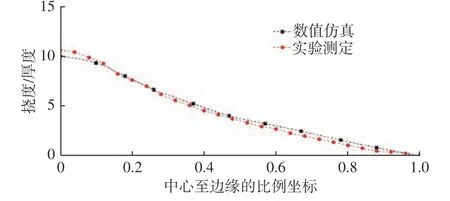
图5 实验与仿真中线处变形轮廓数值对比Fig. 5 Numerical comparison of deformation profile between test and simulation center line

图4 所示的实验与仿真变形模式的对比显示，试件发生了整体永久塑性变形，主要出现在方板中间，数值仿真的位移分布与实验结果一致。图5 所示的数值模拟变形量值与实验结果的对比显示，两者吻合较好，试验板中心最大变形挠度厚度比为10.58，数值仿真板中心最大变形挠度厚度比为9.98，两者的误差为5.67%，小于10%，满足工程精度要求，认为本文所采用的数值计算方法和材料参数合理。

3 冲击波载荷几何参数特征

为研究爆炸冲击波载荷和准静态气压载荷对加筋板变形的影响，设置了2 种载荷，并采用面载荷均布加载形式，如表1 和表2 所示。表1 为初始爆炸冲击载荷参数，设置了4 组冲量值I=2.0，2.5，3.0，3.5 MPa·ms，改变载荷作用时间t和载荷峰值Pm，使冲量保持一致。

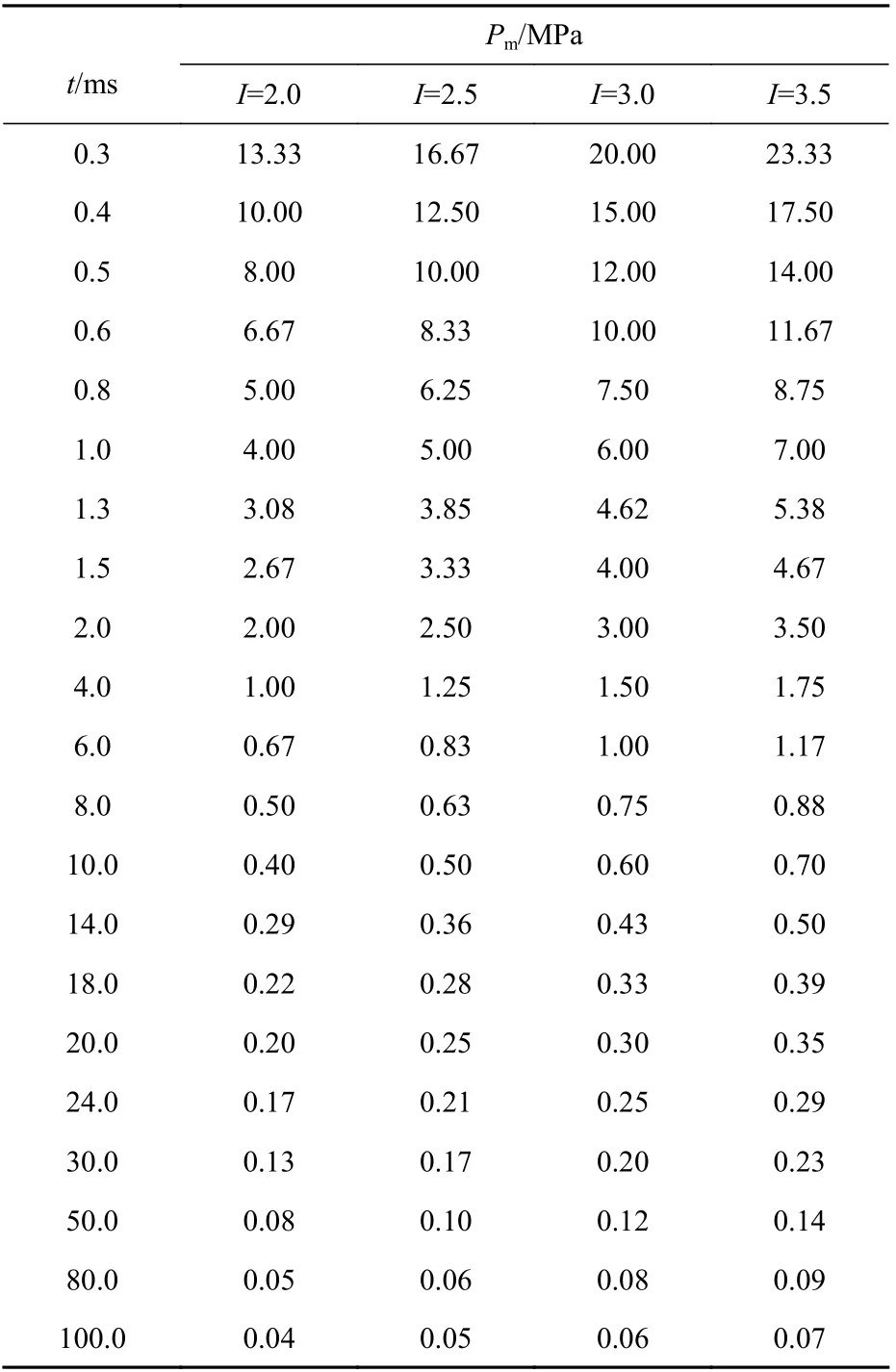
表1 初始爆炸冲击波载荷参数Table 1 Load parameters of initial explosive impact wave

本文采用三角形载荷代替初始爆炸冲击载荷。图6 所示为I=2.0 MPa·ms 时所加载的三角形载荷曲线示意图，载荷作用时间t=0.3～4 ms。表1中其他冲量值下的载荷曲线与图6 所示载荷类似。

表2 所示为准静态气压载荷。将参数分为了4 组，每组参数的载荷峰值Pm相等，分别为0.4 ，0.5，0.6 ，0.7 MPa。以载荷作用时间为变量，发现随着载荷作用时间的增长，冲量逐渐变大。

图7 所示为加载的准静态气压载荷曲线示意图。该图为表2 中冲量载荷峰值Pm=0.4 MPa，载荷作用时间t=0.3～60 ms 时的加载曲线，其他载荷峰值下的载荷曲线与图7 所示载荷曲线类似。

4 数值计算结果与分析

4.1 相同冲量下载荷作用时间对加筋板变形的影响

图8 所示为I=2.0 MPa·ms 的模拟结果。定义加筋板的整体挠度值为加筋板中间位置节点Z方向位移值。如图8 所示，在载荷作用时间t=0.3 ～1.0 ms 时，加筋板挠度值变化为186.8～181.4 mm；在载荷作用时间t=1.3～30 ms 时，加筋板的整体挠度变化为177.5～32.0 mm；载荷作用时间t=50.0～100.0 ms，加筋板整体挠度值变化为23.5～20.0 mm。

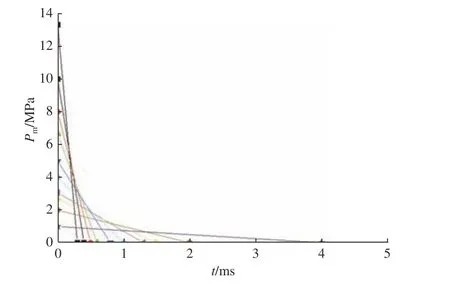
图6 冲击波载荷曲线 (I =2.0 MPa·ms)Fig. 6 Shock wave load curves (I =2.0 MPa·ms)

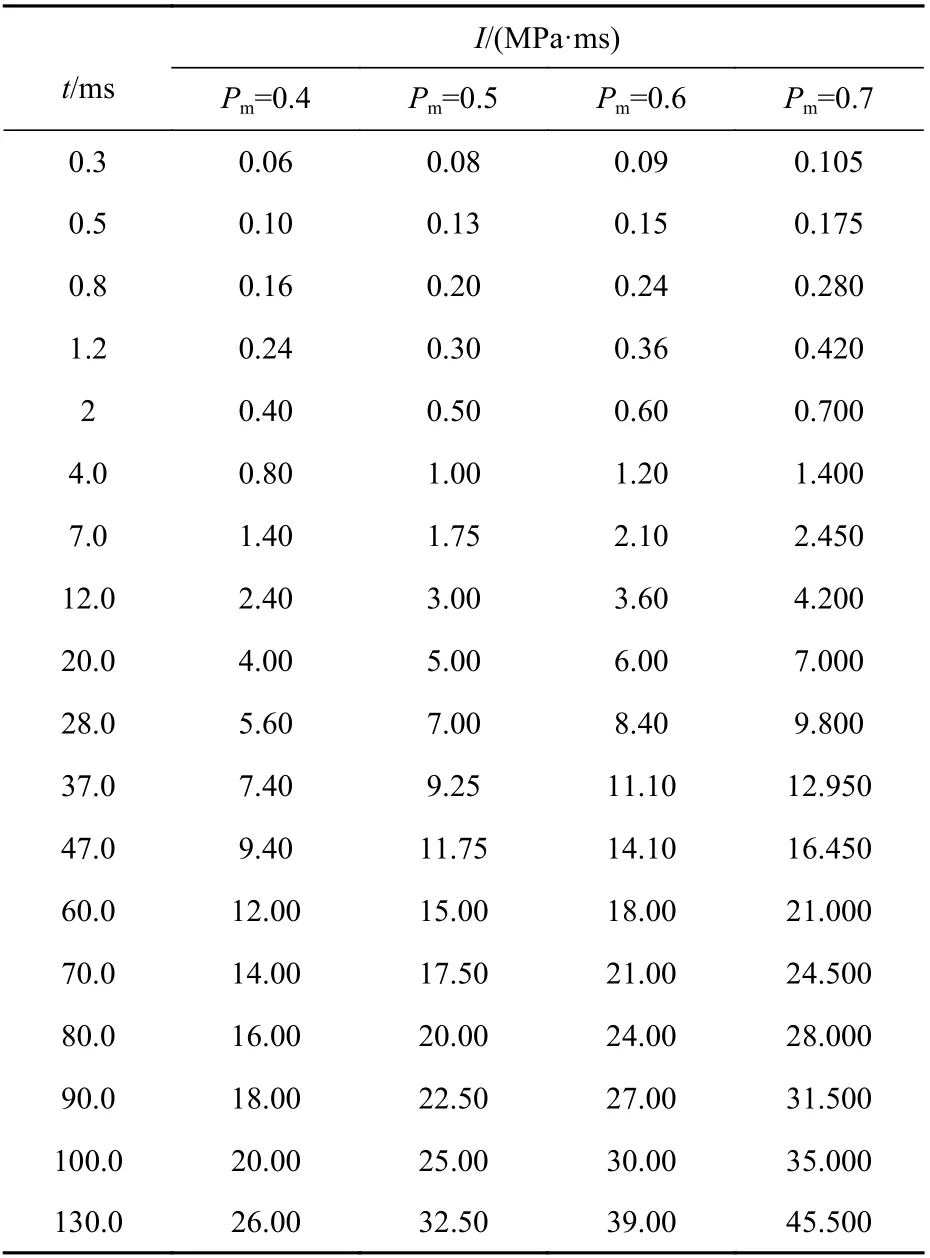
表2 准静态气压载荷参数Table 2 Quasi-static air pressure load parameters

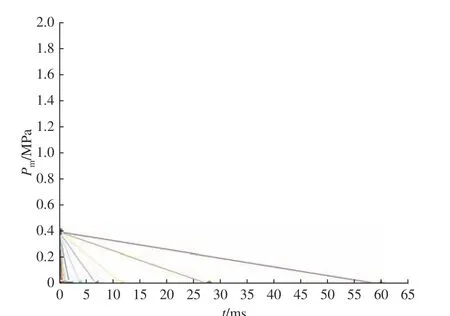
图7 准静态气压载荷曲线 (Pm=0.4 MPa)Fig. 7 Quasi-static air pressure load curves (Pm=0.4 MPa)

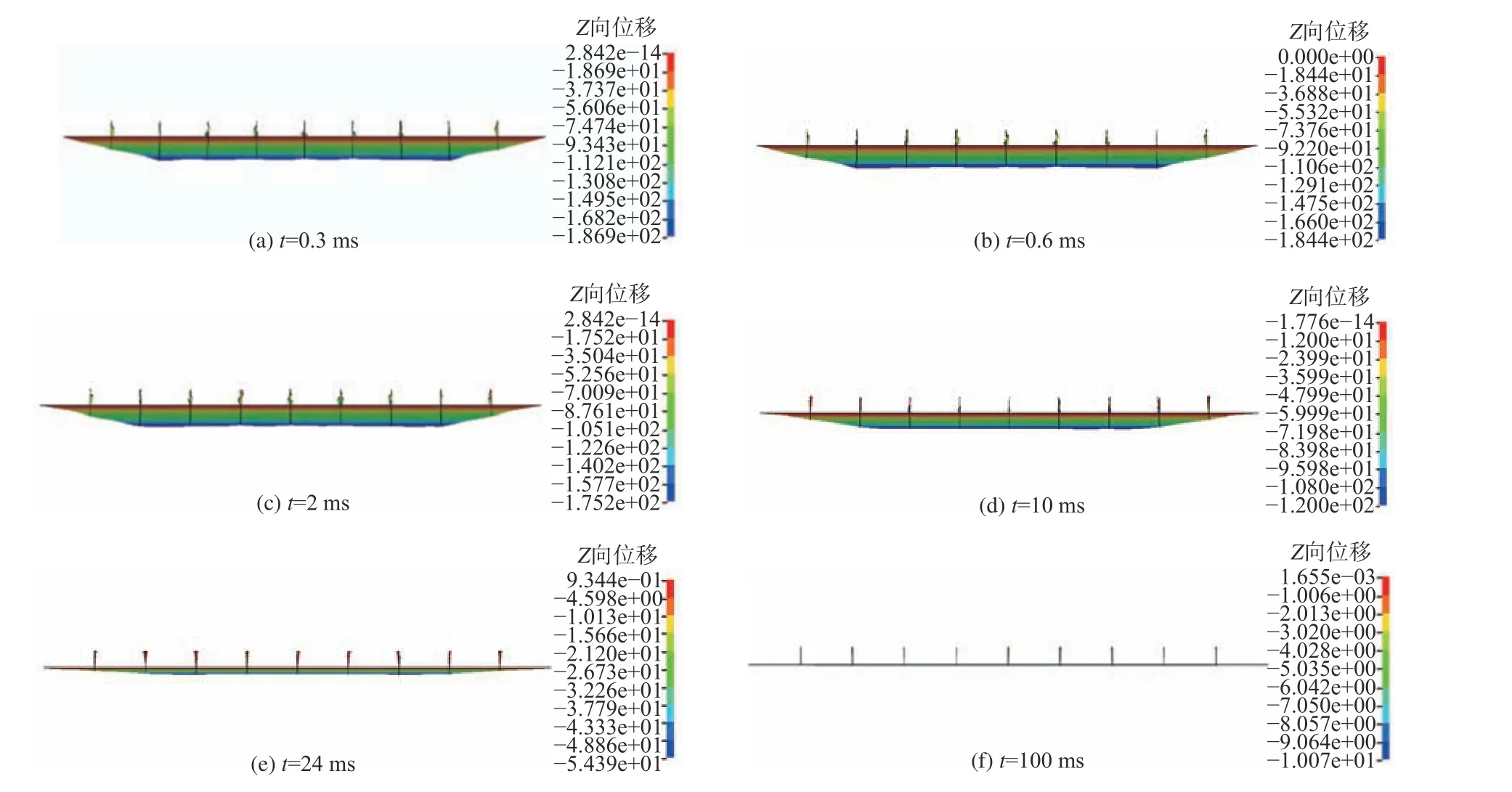
图8 冲击波作用下变形历程位移云图(I=2 MPa·ms)Fig. 8 Displacement contours of deformation history under shock wave (I=2 MPa·ms)

图9 所示为冲量I=2.0 MPa·ms 时板中心位置挠度随载荷作用时间的变化曲线。经计算，得到该加筋板垂向一阶自振周期T=20 ms。由此可知，在载荷作用时间t≤0.05T和t≥2.5T时，加筋板的挠度变化较慢；在载荷作用时间0.065T≤t≤1.5T时，加筋板挠度值减小较快。

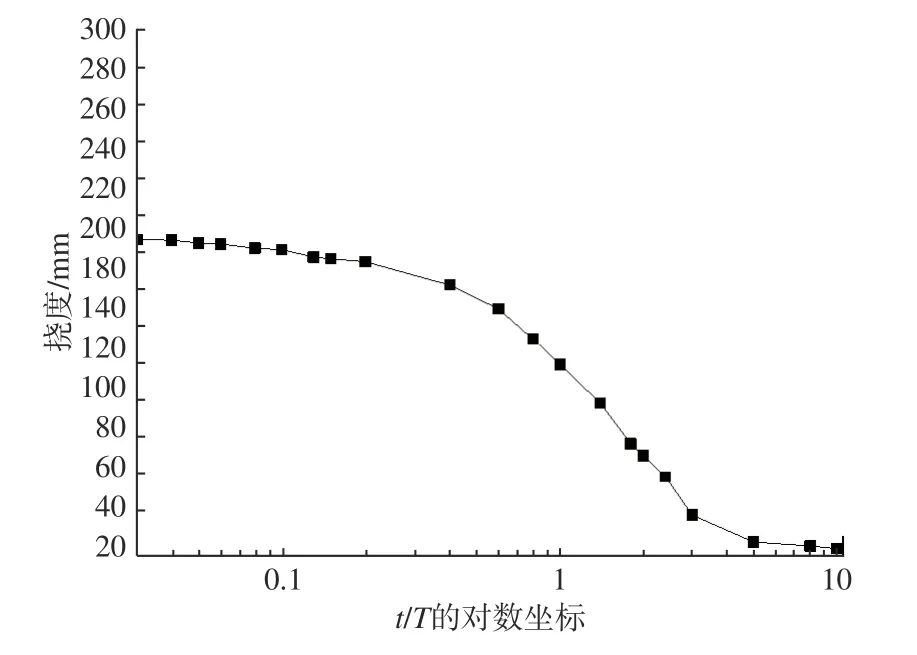
图9 挠度随载荷作用时间t/T 的对数坐标曲线Fig. 9 The logarithmic coordinate curve of the deflection with the load time t/T

当冲量I=2.5，3.0，3.5 MPa·ms 时，加筋板随载荷作用时间的变形规律与图8、图9 所示规律基本一致。将4 种情况下的计算进行汇总比较，结果如图10 所示。

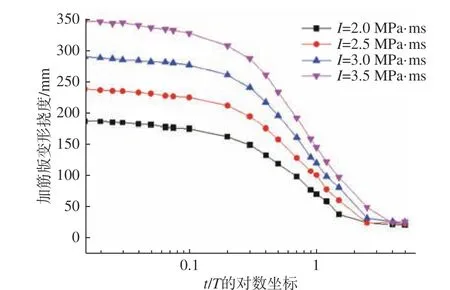
图10 4 种冲击波载荷强度下的挠度计算结果Fig. 10 Deflection calculation results under four kinds of shock wave loading strength

由图10 可知：当冲量I=2.5 MPa·ms，载荷作用时间t≤0.075T和t≥2.5T时，加筋板的挠度变化较慢；在载荷作用时间0.1T≤t≤1.5T时，加筋板挠度值减小较快。当冲量I=3.0 MPa·ms，载荷作用时间t≤0.075T和t≥2.5T时，加筋板的挠度变化较慢；在载荷作用时间0.1T≤t≤1.5T时，加筋板挠度值减小较快。当冲量I=3.5 MPa·ms，载荷作用时间t≤0.04T和t≥2.5T时，加筋板的挠度变化较慢；在载荷作用时间0.04T≤t≤1.5T时，加筋板挠度值减小较快。

由以上数值仿真结果可以看出，当作用在加筋板上的冲量相等且只发生塑性大变形时，可考虑加筋板的自振周期T；当载荷作用时间t<0.05T时，加筋板的挠度值处于最大值附近，且随着载荷加载时间的延长，加筋板的最终挠度值趋于稳定。可以认为，在上述工况中当冲量一定，载荷作用时间t在0.05T内时，与舱内爆炸初始冲击载荷特性一致。当载荷作用时间t>2.5T时，加筋板的最终挠度值处于最小值附近，此挠度为冲击波产生的最终塑性变形，且随着载荷加载时间的延长加筋板塑性变形产生的挠度值将不再变化；当载荷作用时间t处于0.05T～2.5T时，加筋板的挠度逐渐减小，且随着载荷作用时间的增大，加筋板挠度变化量较大。

4.2 载荷峰值相同时载荷作用时间对加筋板变形的影响

根据表2 所示工况，当载荷峰值Pm=0.4 MPa时，模拟结果如图11 所示。

图11 准静态气压载荷作用下变形历程位移云图(Pm=0.4 MPa)Fig. 11 Displacement contours of deformation history under quasi-static air pressure load (Pm=0.4 MPa)

当Pm=0.4 MPa，载荷作用时间t<0.8 ms 时，加筋板变形挠度值小于1.5 mm，相对于所建立的模型尺寸，可以认为加筋板基本没有变形；当载荷作用时间t处于1.2～60.0 ms 时，随着载荷作用时间的延长，加筋板的变形值逐渐增大，挠度变形范围为8.2～208.0 mm；当载荷作用时间t超过70 ms或加载的冲量I=12 MPa·ms 时，加筋板挠度值变为212～220 mm，并且随加载时间延长，加筋板挠度值变化很小。

当Pm=0.5，0.6，0.7 MPa 时，加筋板随载荷作用时间的变形特征与Pm=0.4 MPa 时的基本一致。将4 种工况下的挠度与时间的计算结果汇总作图，结果如图12 所示。

由图12 可知：在载荷峰值较小的情况下，载荷作用时间足够长也会引起加筋板较大的塑性变形。在不同的载荷峰值下，当载荷作用时间t>60 ms时，加筋板挠度值达到最大，且随着载荷作用时间的延长，加筋板挠度值基本不再变化。

即可认为加筋板在不同载荷峰值作用下存在饱和冲量值Is，即当Pm=0.4 ，0.5 ，0.6，0.7 MPa 时，饱和冲量值分别为Is=12，15，18 ，21 MPa·ms。

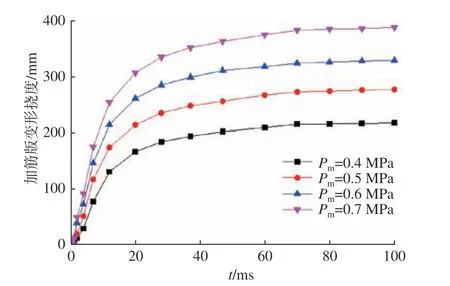
图12 准静态气压载荷作用下挠度随时间变化曲线Fig. 12 Curves of deflection with time under quasi-static air pressure load

可以得到，作用在加筋板上的载荷是随时间增加的，在未达到饱和冲量值以前，决定加筋板最终变形值的为载荷作用时间；在达到饱和冲量值以后，可以认为载荷作用时间不再影响加筋板的最终变形，决定加筋板最终变形值的为载荷峰值。

4.3 两种载荷联合作用下加筋板变形特性

舱内爆炸下，主要载荷形式为初始冲击波载荷与准静态气压载荷联合作用形式。载荷特征可通过小药量舱内爆炸载荷特性实验进行研究。图13所示为舱内爆炸下冲击波压力实验测试结果[3]，图中，P为载荷。

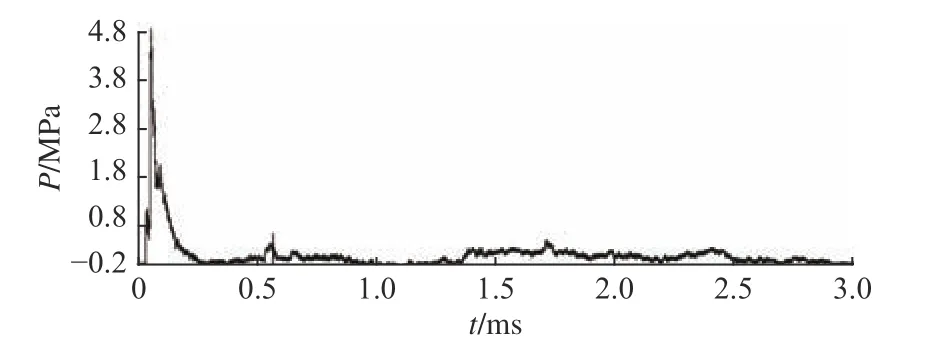
图13 舱内爆炸冲击波压力测试结果Fig. 13 Pressure history of internal blast loading

该实验模型尺寸为1.25 m×0.75 m×0.625 m，使用TNT 炸药，药量为33 g。如图13 所示，初始冲击波作用时间为0.25 ms，载荷峰值为4.8 MPa。在0.5～3.0 ms 间出现了准静态气压载荷，载荷峰值较小，为0.4 MPa。通过该实验工况可以看出，准静态气压载荷作用时间约为冲击波作用时间的10 倍。

由实验测试结果可以看出，初始冲击波载荷与4.1 节相同冲量下载荷作用时间小于0.05T时的载荷特性较为一致；准静态气压载荷与4.2节所描述的载荷曲线（峰值较小、作用时间较长）形式基本一致。

根据以上结果，按照准静态气压载荷作用时间是冲击波载荷作用时间10 倍的关系，进行2 种载荷分别加载和联合加载，分析冲击波载荷（峰值4.8 MPa）和准静态气压载荷(峰值0.4 MPa)对加筋板变形的影响程度。

载荷的施加曲线如图14 所示。

根据上述加载曲线进行数值仿真。由于Pm较小，为了得到较为明显的变形情况，在仿真中设置板厚为1.5 mm，加强筋高度不变，厚度为2.0 mm，仿真结果如图15 所示。

由图15 可以看出：将爆炸冲击波载荷单独作用到加筋板上时，加筋板的最终变形挠度值为183.6 mm；将准静态气压载荷单独作用到加筋板上时，加筋板的最终变形挠度值为85.2 mm；当2 种载荷联合作用到加筋板上时，加筋板的最终变形挠度值为298.0 mm。可以得出，在舱内爆炸载荷作用下，对加筋板架结构的变形起主要作用是初始爆炸冲击载荷，且最终变形不是2 种载荷作用下的简单叠加，2 种载荷的联合作用会加剧加筋板架结构的变形，也即可以认为2 种载荷的联合作用会增强其毁伤效果。

在舱内爆炸中，初始爆炸冲击波载荷的峰值较大，虽然作用时间较短，但加筋板变形主要发生在初始冲击波作用这个阶段；当初始冲击波作用之后，准静态气压载荷继续作用，该载荷与初始冲击波载荷相比相对较小，作用时间相对较长，对加筋板的塑性变形同样有贡献作用。

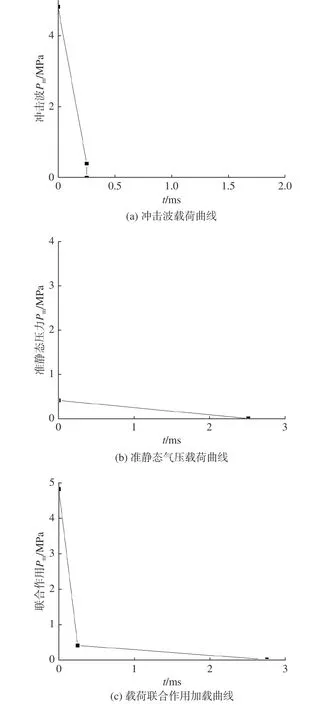
图14 联合作用载荷曲线生成示意图Fig. 14 Schematic diagram of load curves generation under combined action

5 结 论

分别在相同冲量和峰值的条件下，利用非线性动力有限元分析软件LS-DYNA 对随载荷作用时间变化的加筋板变形特性进行了数值模拟，验证了所建立模型的准确性，并分析了加筋板分别在爆炸冲击载荷、准静态气压载荷以及2 种载荷联合作用下的变形特性，得到了以下主要结论：

图15 3 种载荷形式下的计算结果对比Fig. 15 Comparison of calculation results under three load forms

1） 当作用在加筋板上的冲量相等且只发生塑性大变形，载荷作用时间t<0.05T时，该载荷与舱内爆炸初始冲击载荷的特性一致，加筋板的最终变形挠度值处于最大值附近，且随着载荷加载时间的延长，加筋板的挠度值变化较小。

2） 在载荷峰值相同，未达到饱和冲量值以前，决定加筋板最终变形挠度值的是载荷作用时间；在达到饱和冲量值以后，可以认为载荷作用时间不再影响加筋板最终变形挠度值，决定加筋板最终变形挠度值的是载荷峰值。

3） 在舱内爆炸载荷作用下，最终变形挠度值不是2 种载荷作用下的简单叠加，2 种载荷的联合作用会加剧加筋板架结构的变形，即可以认为2 种载荷的联合作用会增强其毁伤效果。