基于体积力模型的潜艇应急上浮运动数值模拟分析

魏可可，高霄鹏

海军工程大学 舰船与海洋学院，湖北 武汉 430033

0 引 言

潜艇的应急上浮是指当发生舱室破损进水、卡舵等事故时，采取排除部分或者全部主压载水舱内的水，从而使潜艇迅速浮出水面的一种紧急操纵措施。为保证潜艇应急上浮的安全性和稳定性，准确预报潜艇在应急上浮过程中的运动特性十分有必要。

和正常的上浮相比，潜艇应急上浮中艇的排水方式不同且排水速率快，艇体姿态变化幅度大。常见的潜艇应急上浮运动预报方法是通过拘束模试验[1-4]或参数辨识[5]等方法求解水动力系数，然后再基于六自由度运动模型进行预报。戴余良等[6-7]应用非线性系统运动稳定性与分叉理论，以及同伦延拓数值计算方法，分析了潜艇应急上浮运动的稳态响应及运动稳定性。王晓玢等[8]通过对潜艇垂直面操纵运动进行非线性建模，利用分叉与突变理论方法对潜艇上浮运动中由静态分叉和动态分叉引发的状态突变进行了分析。潜艇水动力系数的求解较复杂且有一定的难度，而上述预报方法主要是针对潜艇某自由度上的运动，并不能真实反映潜艇在六自由度完全释放情况下的应急上浮运动特性，且预报精度还有待提高。

随着计算机技术的快速发展，计算流体力学在船舶运动研究中的应用越来越广泛。Carrica等[9-10]基于自主研发的流体软件CFDShip-Iowa V4，实现了不同工况下潜艇六自由度运动的数值模拟计算，并对其操纵性进行了较高精度的预报。Chase 等[11]采用重叠网格技术，对Suboff 潜艇模型的直航拖曳和自由自航等运动进行了数值模拟计算。周广礼等[12-13]基于RANS 方程及流体体积模型，采用整体动网格技术，对Suboff 模型的应急上浮六自由度运动及其出水运动予以了研究。廖欢欢等[14]采用流体体积法（volume of fluid，VOF）六自由度求解器和重叠网格技术，研究了潜艇在一定潜深下的应急上浮六自由度运动，并对上浮过程中的姿态和水动力进行了分析。

以上大多学者对潜艇应急上浮运动的研究都没有考虑螺旋桨以及初始航速等问题的嵌入，为此，本文将基于STAR-CCM+软件平台，采用基于体积力模型的虚拟桨盘，针对潜艇在不同航速下的应急上浮运动进行数值模拟，并对比分析潜艇在应急上浮运动中的姿态和上浮运动时间等，用以为潜艇在实际中的上浮运动操控提供一定的借鉴。

1 计算对象

本文将以美国泰勒研究中心提供的Suboff 潜艇试验模型为研究对象。国内外针对该模型开展了大量的拖曳及流场测量试验，其三维模型图如图1 所示，模型主尺度参数如表1 所示。

图1 Suboff 潜艇三维模型Fig. 1 Three dimensional model of Suboff submarine

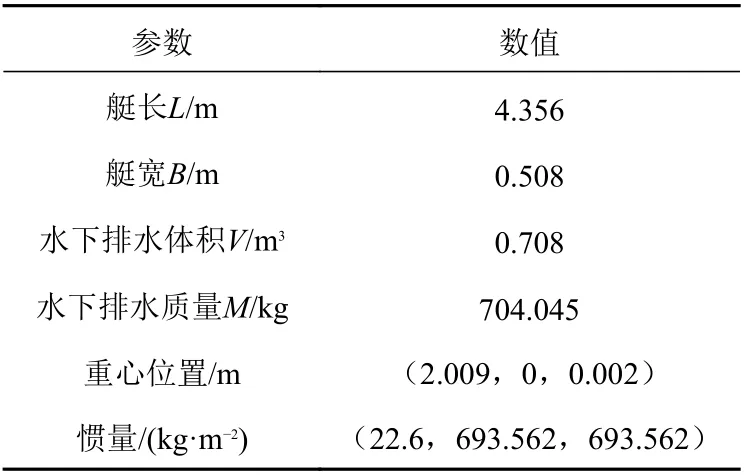
表1 模型主要参数Table 1 Main parameters of the model

2 数值模拟

2.1 控制方程及湍流模型

应用黏流CFD 方法开展数值计算的基础是纳维−斯托克斯（Navia-Stokes，N-S）方程，然而受限于计算能力，当前还不能通过直接求解N-S 方程（direct numerical simulation，DNS）来获得潜艇周围复杂的黏性流场。将N-S 方程中的湍流脉动项进行时均化处理可以极大地减小计算量，所得雷诺平均方程（RANS）的具体表达如式（1）所示。然而，N-S 方程在时均化的过程中增加了含未知量时均的雷诺应力项，通过引入湍流模型，可使方程封闭。目前，该方法已在舰艇流体力学理论研究及工程实践中得到广泛应用。

开展计算时，控制方程离散均采用二阶迎风格式，并应用分离式解法（segregated flow）对离散后的方程组进行求解。压力速度耦合迭代采用SIMPLE 算法，涉及非稳态计算时，设定计算过程中的时间步长为 ∆t且固定不变，时间迭代采用二阶形式，即

采用RANS 方法开展潜艇水动力计算时，湍流模型的选取是确保计算精度的关键要素，众多学者已针对该问题开展了大量研究，但所得结论存在较大的不同，且湍流模型的适用性也与网格布局及操作者的数值计算经验相关。综合各类文献资料，本文选取Wilcoxk−ω 与SSTk−ω湍流模型进行优选分析。

Wilcoxk−ω湍 流 模型 最 早由Wilcox 于1988年提出，后经过不断的修正，模拟精度及其适用范围均得到了提升，STAR-CCM+软件平台中就提供有最新的修正模型，具体表达形式如下：

式中：k为湍动能； ω为特殊湍动能耗散；其余参数的具体定义及参数值参见文献[15]。

Menter 等[16]结 合 标 准k−ε 与k−ω湍 流 模 型，提出了剪切应力模型SSTk−ω，式（4）给出了该模型的最新修正形式，具体推导过程及参数定义详见文献[15]。

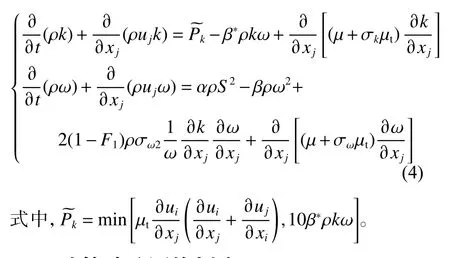
2.2 计算域及网格划分

计算域选取为方形域，除域尾端边界设置为压力出口外，其余边界条件均设置为速度入口，域大小及计算域与自由液面的初始相对位置如图2 所示。

进行网格划分时，为能更好地捕捉两相流自由液面，对自由液面可能通过的区域进行了网格加密。此外，为准确模拟潜艇出水后艇体周围的流场，对模型首部及指挥室围壳周围网格进行了细化处理。同时，为满足网格贴体的要求，对近壁面区域进行了局部加密，以确保艇体壁面y+在30～300 之间[12]。当y+在30～200 之间时，表征第1 层网格布置于对数层，可通过假定的壁面函数对近壁面流动进行模拟。该方法不直接求解黏性底层与过渡层内的流动，适用性较强，可极大地减少近壁面网格数量。艇体表面、域剖面及近壁面域的网格如图3 所示，网格总数为700 万。

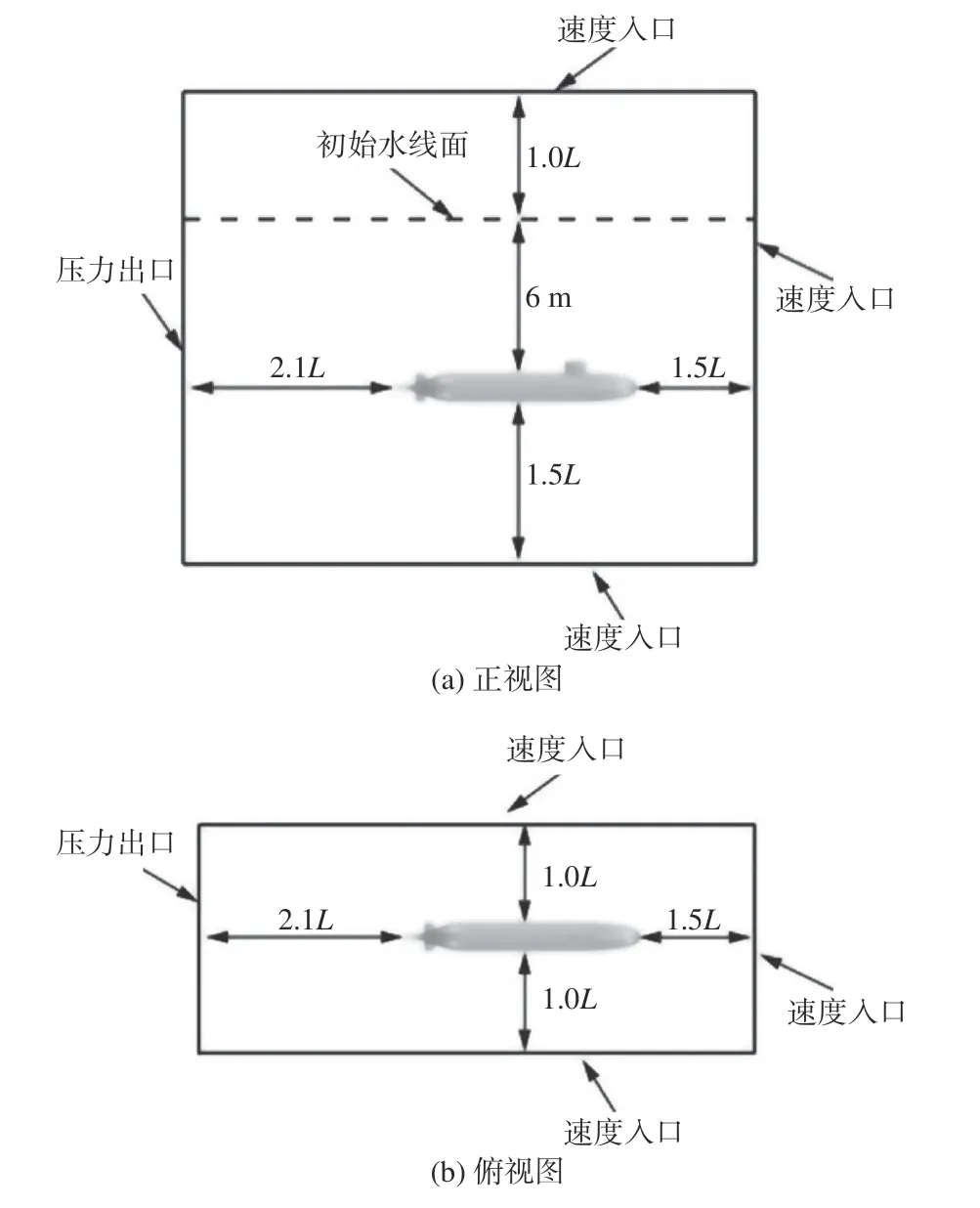
图2 计算域及边界条件Fig. 2 Computational domain and boundary conditions

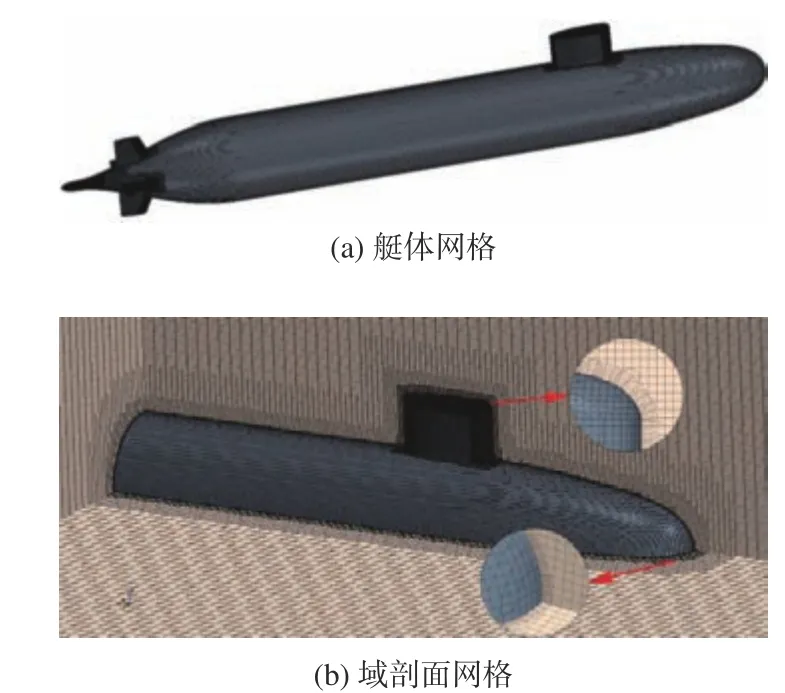
图3 艇体整体网格及域剖面网格Fig. 3 Overall grid and domain profile grid of hull

2.3 体积力模型

通过对螺旋桨入流面流速进行加权积分，获得桨的进流速度，然后代入到已知螺旋桨水动力曲线中，预估得到推力及扭矩，接着，通过添加源项的方式，对设定的体积力域内的流体施加等效的力及力矩，该方法即为体积力模型。体积力模型不仅能够将力及力矩施加于潜艇上，而且能更为准确地模拟由螺旋桨引起的潜艇尾流场变化，相较于直接力模型，其计算量大，但计算效率远优于开展的真实螺旋桨计算。

为了重点分析潜艇的运动特征，提高计算效率，螺旋桨用基于体积力模型的虚拟桨代替。该虚拟桨的参数采用DTMB 4 383 标准桨的，模型主参数如表2 所示。

表2 DTMB 4 383 螺旋桨主要参数Table 2 Main parameters of DTMB 4 383 propeller

2.4 数值计算的验证

针对漂角 β=2◦～14◦、 间隔 2◦的Suboff 模型的无因次纵向水动力X′进行数值计算，计算结果与试验值[17]的对比如图4 所示。

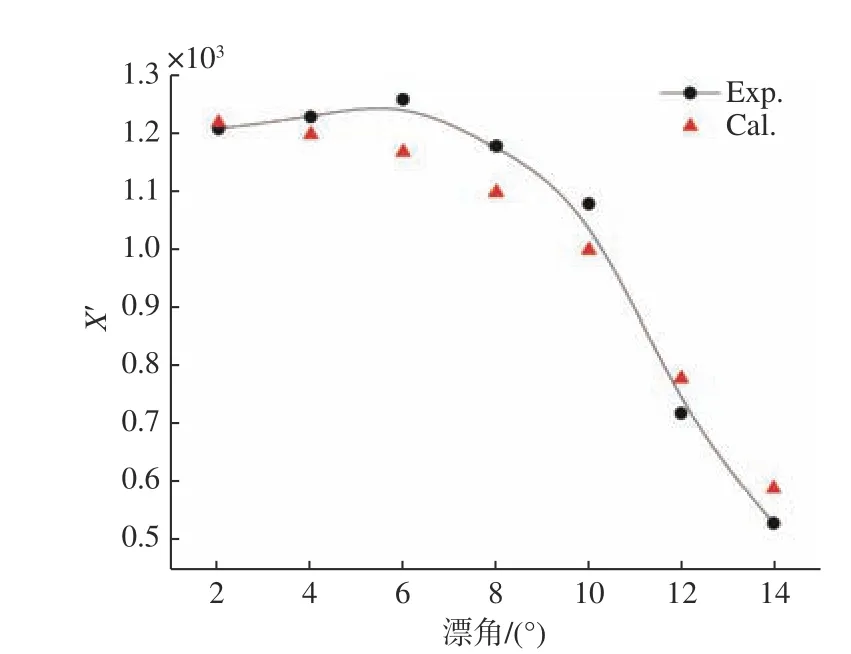
图4 不同漂角下艇体纵向水动力的试验值与数值计算值的对比Fig. 4 Comparison between experimental and numerical values of longitudinal hydrodynamics of the hull at different drift angles

由图4 可看出，不同漂角下艇体纵向水动力数值计算结果与试验值吻合良好，证明该方法可行。因此，选取该方法进行后续的数值仿真计算。

2.5 计算工况

为探讨不同航速对潜艇上浮运动的影响规律，选取上浮力为总排水量的5%、螺旋桨转速分别为300，400，500，600 r/min 的工况进行数值模拟计算，具体计算工况如表3 所示。

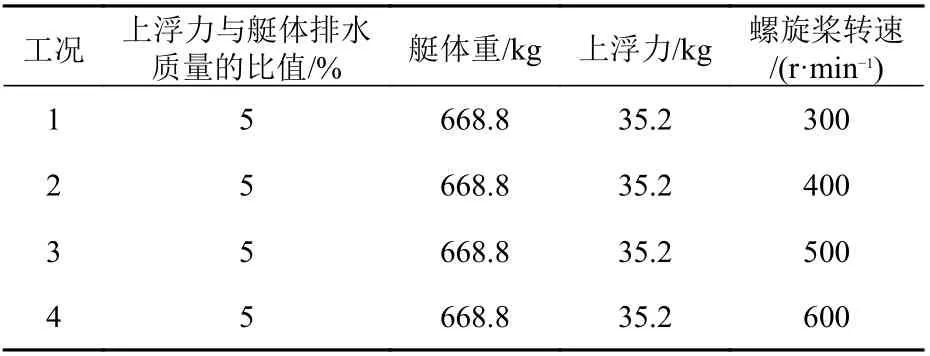
表3 计算工况Table 3 Calculation conditions

3 不同航速下数值模拟结果分析

3.1 螺旋桨转速与航速的匹配

假定潜艇上浮之前在水下做定深直航运动，为获取模型水下稳定直航状态，设定初始直航航速U=0，在螺旋桨推力的作用下，潜艇沿x方向做直航运动。为避免在初始计算阶段出现计算结果不稳定的现象，在t=0～4 s 时间段内将艇体按静态处理，待螺旋桨推力及流场计算结果稳定后，即在t1时刻，将x方向运动完全释放，潜艇开始做直航运动。

不同转速下螺旋桨推力及艇体阻力的时历曲线如图5 所示。由图可知，艇体阻力及螺旋桨推力随时间逐渐向自航值逼近，且二者随时间的绝对变化率较为相近，航速随时间逐步增大并在t2时刻后趋于稳定；随着转速的增大，螺旋桨获得的推力以及艇体的阻力值越大，其运动稳定的时间就越短，最终稳定的航速值也越大，这从图6 即可看出。

表4 给出了不同转速下潜艇做定深直航运动时的计算结果。由表4 可知，4 个转速下t1值间的差别较小，在t2时刻是随转速的增大而减小，转速越大，需要稳定的时间就越短；转速为300～600 r/min 时，最终稳定的定深下的航速分别为0.97，1.35，1.72 和2.1 m/s。

3.2 艇体上浮运动

图7 给出了不同转速下艇体垂向位移运动的时历曲线。由图可知，艇体做应急上浮至出水一般会经历水下定深直航运动—上浮运动—水面航行这3 种状态的运动。当螺旋桨转速为300 r/min时，其水下定深直航时间为101 s，上浮时间8 s，上浮出水的时刻为109 s；当转速为400 r/min 时，其水下定深直航时间为92 s，上浮时间9 s，上浮出水的时刻为101 s；当转速为500 r/min 时，其水下定深直航时间为91 s，上浮时间9 s，上浮出水的时刻为100 s；当转速为600 r/min 时，其水下定深直航时间为71 s，上浮时间12 s，上浮出水的时刻为83 s。由此可知，随着转速的增大，潜艇获得稳定航速的时间越短，艇体在水下做定深直航运动的时间也就越短；不同转速下艇体上浮的时间虽然有所差别，但其差值量级较小，上浮运动的时间主要还是受上浮力的影响；同时，潜艇的上浮运动是一个非线性的复杂的六自由度运动，当上浮力一致时，螺旋桨转速越大，其上浮运动速度不一定越大。

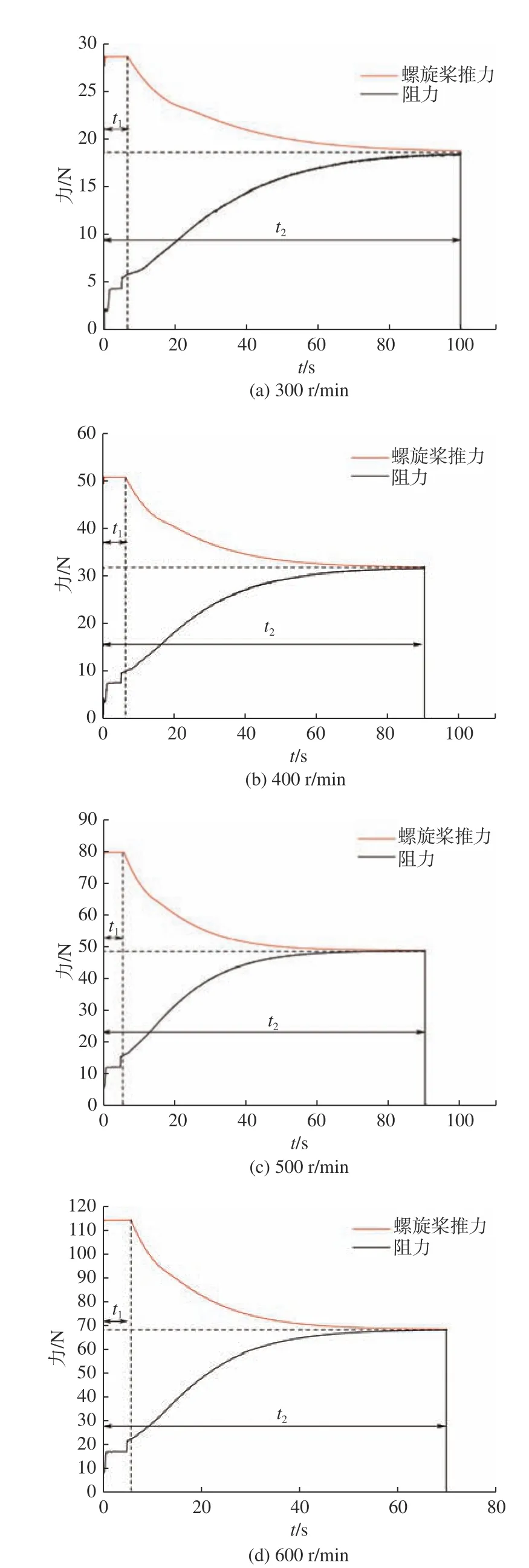
图5 不同转速下艇体阻力和螺旋桨推力时历曲线Fig. 5 Time histories of hull resistance and propeller thrust at different rotation speeds

图6 不同转速下艇体航速的时历曲线Fig. 6 Time histories of hull velocity at different rotation speeds

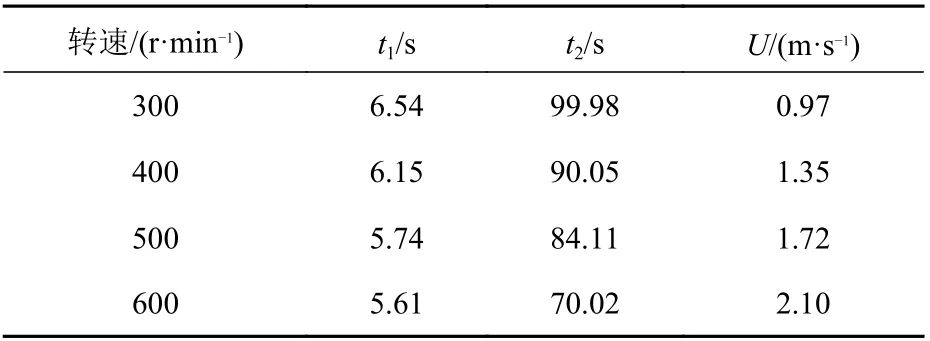
表4 潜艇定深直航运动计算结果Table 4 Calculational results of direct sailing motion of submarine at fixed depth

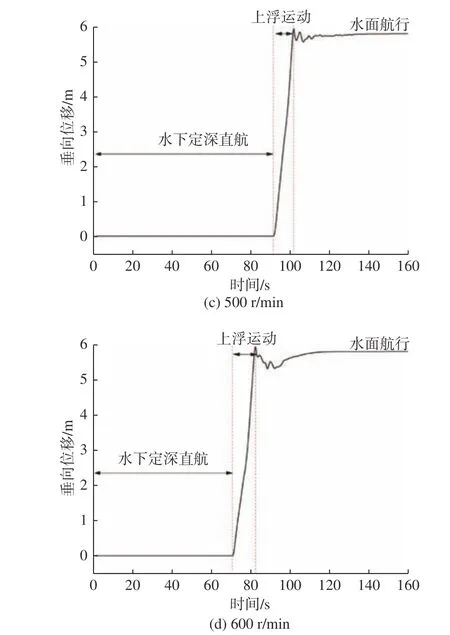
图7 不同转速下艇体的垂向位移运动时历曲线Fig. 7 Time histories of vertical displacement motion at different rotation speeds

3.3 艇上浮时的姿态分析

3.3.1 纵倾角分析

图8 所示为不同转速下艇体纵倾角的时历曲线，表5 给出了纵倾角第1 次产生变化的时刻、发生峰值的时刻、峰值以及来回振荡波动的时间。由图8 和表5 可知，当转速为300 r/min 时，纵倾角第1 次产生变化的时刻是100.2 s，第1 次产生峰值的时刻是109 s，其峰值为−22°，纵倾角来回振荡波动的时间是29.8 s；当转速为400 r/min时，纵倾角第1 次产生变化的时刻是92 s，第1 次产生峰值的时刻是99 s，其峰值为−23°，纵倾角来回振荡波动的时间是47 s；转速为500 r/min 时，纵倾角第1 次产生变化的时刻是91 s，第1 次产生峰值的时刻是96 s，其峰值为−22°，纵倾角来回振荡波动的时间是47 s；当转速为600 r/min 时，纵倾角第1 次产生变化的时刻是71 s，第1 次产生峰值的时刻是75 s，其峰值为−27°，纵倾角来回振荡波动的时间是54 s。结果显示，随着转速的增大，纵倾角第1 次产生变化及峰值的时刻呈减小趋势，而纵倾角来回振荡波动的时间则越来越大，即转速越大，艇体出水时受自由液面扰动越小。纵倾角的峰值变化主要发生在潜艇上浮运动过程中，来回振荡波动主要发生在潜艇出水时刻。对比3.2 节有关上浮的时刻可知，无论转速多大，潜艇第1 次倾角的峰值都是发生在潜艇上浮运动过程中，由对比分析可知，随着转速的增大，纵倾角的峰值并未呈现出明显的变化规律。

图8 不同转速下艇体纵倾角时历曲线Fig. 8 Time histories of trim angle at different rotation speeds

表5 不同转速下纵倾角的分析Table 5 Analysis of trim angle at different rotation speeds

3.3.2 横倾角分析

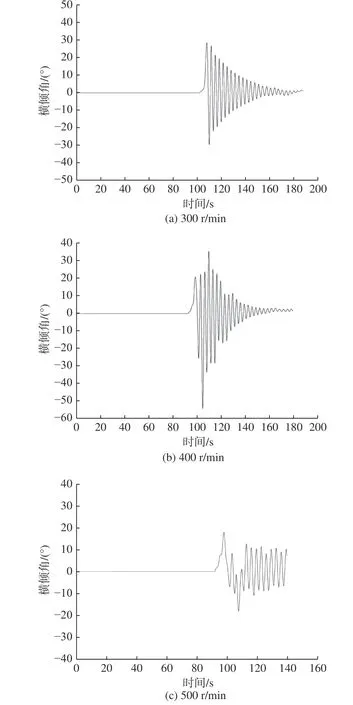
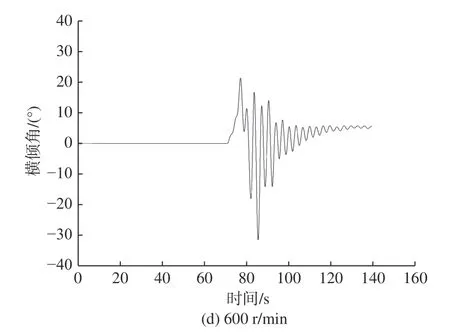
图9 不同转速下艇体横倾角时历曲线Fig. 9 Time histories of heeling angle at different rotation speeds

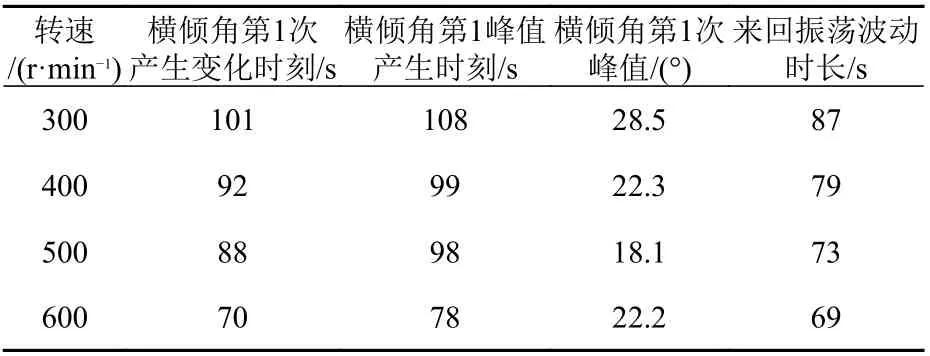
表6 不同转速下横倾角的分析Table 6 Analysis of heeling angle at different rotation speeds

图9 所示为不同转速下艇体横倾角的时历曲线，表6 给出了横倾角第1 次产生变化的时刻、发生峰值时刻、峰值大小以及来回振荡波动的时间。由图9 和表6 可知，当转速为300 r/min 时，横倾角第1 次产生变化的时刻是101 s，第1 次产生峰值的时刻是108 s，其峰值为28.5°，横倾角来回振荡波动的时间是87 s；当转速为400 r/min时，横倾角第1 次产生变化的时刻是92 s，第1 次产生峰值的时刻是99 s，其峰值为22.3°，横倾角来回振荡波动的时间是79 s；当转速为500 r/min时，横倾角第1 次产生变化的时刻是88 s，第1 次产生峰值的时刻是98 s，其峰值为18.1°，横倾角来回振荡波动的时间是73 s；当转速为600 r/min时，横倾角第1 次产生变化的时刻是70 s，第1 次产生峰值的时刻是78 s，其峰值为22.2°，横倾角来回振荡波动的时间是69 s。结果显示，随着转速的增大，横倾角第1 次产生变化时刻和发生峰值的时刻以及来回振荡波动的时间越来越小。横倾角的峰值变化主要发生在潜艇上浮运动过程中，来回振荡波动主要发生在艇出水时刻。对比3.2 节有关上浮的时刻可知，无论转速是多少，潜艇第1 次横倾角的峰值均发生在潜艇上浮运动过程中，随着转速的增大，横倾角的峰值并未呈现出明显的变化规律。

4 结 语

本文基于体积力模型的虚拟桨盘模型，对不同转速下潜艇的水下定深直航、六自由度上浮、出水以及水面航行进行了数值模拟，并对比分析了不同转速下潜艇螺旋桨与转速的匹配及其姿态等，该方法可为潜艇的应急上浮运动提供一定的参考。

通过对比分析不同转速下艇体上浮运动过程中的姿态，可得出如下结论：随着转速的增大，潜艇获得稳定航速的时间越短，艇体在水下做定深直航运动的时间也越短；不同转速下其上浮运动的时间相差不大；转速越大，无论是纵倾角还是横倾角，其倾角第1 次产生变化的时刻和发生峰值的时刻会越来越小；同时随着转速的增大，纵倾角的来回震荡波动时间会越来越长，而横倾角的来回震荡波动时间则越来越短，且倾角的峰值随转速的变化并未呈现出明显的变化规律。