Permeability differences based on three-dimensional geometrical information of void spaces

De-Sung Cheon, Mnu Tkhshi, Tehyun Kim

a Geology Division, Korea Institute of Geoscience and Mineral Resources, Daejeon, South Korea

b Hydrology Research Group, National Institute of Advanced Industrial Science and Technology, Tsukuba, Japan

c Rad waste Disposal Research Division, Korea Atomic Energy Research Institute, Daejeon, South Korea

Keywords:X-ray computed tomography (CT)Porosity Permeability Geometrical information Three-dimensional medial axis (3DMA)

ABSTRACT In this study,the permeabilities of Berea and Otway sandstones were measured under different confining pressures, and porosity was investigated through mercury intrusion porosimetry (MIP).The total porosities of the Berea and Otway sandstones were approximately 17.4% and 25%, respectively.Pore size distributions of each sandstone were almost the same, but the pores in the Otway sandstone were slightly narrower.However,the permeability of the Otway sandstone was smaller than that of the Berea sandstone by one order of magnitude.Three-dimensional(3D)void geometry and geometrical properties of the void spaces relevant to flow were compared to obtain the relation between the permeability differences and porosities of the two sandstones.The 3D geometrical analysis using microfocus X-ray computed tomography(CT)was performed,and the pore geometries of both sandstones were compared using the 3D medial axis (3DMA) method.Pore and throat radii, pore coordination number, tortuosity,number of connecting paths, connecting path volume, and other factors were determined using 3DMA.The Otway sandstone was characterized by a small effective throat/pore radius ratio.Based on the fluid flow mechanism, the lower effective throat/pore radius ratio results in a lower permeability induced by the fluid energy loss,which means that the 3D geometrical shape of void spaces affects the permeability value.

1.Introduction

In the context of carbon dioxide (CO2) deep geological sequestration,it is essential to investigate the flow characteristics of CO2in the storage layers.The permeability and storability related to the flow and transport are critical parameters to evaluate the storage capacity of oil, natural gas and CO2aquifer at deep underground rock and sedimentary layers.Generally, sandstone layers are important candidates of proper reservoirs for storage of resources and CO2because of their high porosity and preferential fluid flow properties.The mechanical and hydraulic characteristics of sandstone depend on the structures of sand grains and the void space in it.The geometry of void space structure in porous sandstone also plays a fundamental role in fluid transport(Takahashi et al.,2014).

CO2geological storage in saline aquifers should be located at a minimum of 800 m depth.Therefore,flow characteristics,including permeability,should be evaluated with depth to accurately predict CO2behavior.Many previous studies have been performed to examine the relationship between the permeability and the effective pressure of porous sandstone.Zhu and Wong (1997) reported the relationship between the permeability and various stress states of sandstones during the brittle-ductile transition.They evaluated the permeability variations depending on porosity, effective confining pressure and strain, and investigated the permeability evolution regarding mechanical deformation.Takahashi et al.(2006) investigated porosity evolution under different deformation regimes, and showed that the pore structural changes at a microscopic scale depend on mechanical deformation.

It is widely accepted that pore structure is closely related to the permeability, and correlations between the permeability and porosity in different forms such as proportional form (Katz and Thompson,1986; Luffel et al.,1991; David et al.,1994), power-law(Luquot and Gouze, 2009; Luhmann et al., 2014; Luquot et al.,2014) and exponential form (Chin et al., 1998; Rutqvist et al.,2002) are well developed.However, the correlations between the permeability and porosity depend on the complex pore geometry,such as spatial information and size distribution of pore channels.Therefore, it is difficult to affirm appropriate flow mechanism through pore channels,and hence the analysis of pore geometrical characteristics can be a useful way for understanding the flow mechanism (Costa, 2006; Lei et al., 2007; Nelson, 2009; Xu et al.,2018).

Various methods have been tested to clarify and visualize the complex interaction of pore geometry.Mercury intrusion porosimetry (MIP) can quantify the total porosity and pore size distribution in rocks (Swanson,1981; Katz and Thompson,1986,1987;Pittman,1992; Rezaee et al., 2006), but it cannot provide geometrical and spatial information on void spaces.Recently, X-ray computed tomography (CT) has been widely used as a common non-destructive tool in various fields, and some recent progress using X-ray CT in rock mechanics and rock engineering has been achieved.Lindquist et al.(2000) measured geometrical properties of void spaces with pore volume and channel length in sandstone using synchrotron X-ray CT.Coles et al.(1996) investigated the porosity and pore size distributions of sandstone using microfocus CT and also measured the hydraulic conductivity values.Karacan et al.(2003) used X-ray CT to evaluate the porosity change of limestone under triaxial compression condition, and Hirono et al.(2003) measured the permeability of fault-related rocks with three-dimensional(3D)fluid flow distributions through medical CT and characterized the flow in the fault zones depending on the deformation mechanisms.Otani and Obara(2004)applied X-ray CT in non-destructive testing systems for estimating the mechanical properties of geomaterials.As described above,X-ray CT is a useful visualization tool for non-destructive and non-contact assessments,but there is a lack of understanding of the effect of 3D pore geometry on flow mechanism through pore channels.

In this study, we used microfocus X-ray CT with a high resolution of 10 μm to visualize and measure the 3D void space in sandstone.In the X-ray CT images, porous media appear in grayscale and show bimodal populations corresponding to the features of pore and grain spaces, respectively.Therefore, a valid segmentation procedure is required to focus on the pore structure and qualification of the pore space geometry.We used 3D medial axis(3DMA)method to measure the geometrical properties of the void structures relevant to the flow in porous media, which has been widely used in the pore structure analysis (Lindquist and Venkatarangan, 1999; Lindquist et al., 2000; Cai et al., 2009;Dewers et al., 2012; Armstrong et al., 2015).

Fig.1.Assembly of the specimens having 50 mm diameter and 25 mm height for the flow pump test: (a) Berea and (b) Otway sandstone specimens.

We also evaluated the permeability evolutions under various confining pressures in Berea and Otway sandstones.Based on the results,we investigated the relation between the permeability and geometry of voids to clarify the permeability difference using the microfocus X-ray CT and 3DMA.The number of connecting paths,tortuosity, the shortest path distribution, and connecting path volume within an arbitrary region were analyzed.We also presented the spatial distribution of void spaces at every pore size.The Otway and Berea sandstones were characterized by an effective throat/pore radius ratio using the geometrical information.Finally,based on the test results of each specimen, we investigated the effect of 3D geometrical characteristics of the void spaces on the fluid flow mechanism.Additionally, the effect of correlation between the radius ratio and adjacent voids on the permeability of sandstones was examined.

2.Specimens and experimental methods

2.1.Specimens and their features

Two types of sandstone were used to evaluate the relation between the permeability and void geometrical information.Otway sandstone(Fig.1a)was obtained from the Paaratte formation in the Otway Basin in Australia,and Berea sandstone(Fig.1b)was widely recognized as a reference material in the field of oil and gas.

The CO2CRC Otway Project is a demonstration project for deep geological storage of CO2in Australia.Sandstone layers consisting of the lithology of Otway Basin are proper reservoirs to store CO2due to their high porosity (usually more than 25%) and adequate fluid flow and transport properties.The sandstone specimens were cored at the depth between 1501 m and 1512 m,which is the target position for CO2storage.

Berea sandstone is well consolidated and fine-grained.However,the grains are more angular than rounded, hence it is ideally abrasive.Based on the previous studies, the permeability ranged from 19 mD to 2500 mD at porosities of 13%-23% (Cleveland Quarries, 2020), showing relatively high porosity and permeability.Previous researchers reported changes of the permeability of Berea sandstone under different confining pressures and temperatures.Dey (1986) repeatedly raised and lowered the effective confining pressure between 3.5 MPa and 31.5 MPa and found that the permeability of Berea sandstone decreased by 30%.For low and high(up to 250 MPa)effective pressures and hydrostatic cases,Zhu and Wong(1996)reported that the permeability of Berea sandstone showed a rapid decrease with the increase of effective mean stress.Rosenbrand et al.(2014, 2015) also observed the reduction of permeability when increasing the temperature of specimen up to 80°C due to the mobilization of fine particles in the pore.

2.2.Experimental methods

For the experimental procedure, the specimens for each test were prepared separately.First, we evaluated the porosities and pore size distributions of the cylindrical specimens by MIP using an AutoPore IV 9520 before measuring the permeability.The mercury porosimeter measures the diameter of the pore ranging from 3.6 μm to 360 μm.In the pore analysis,the test is mainly performed by two-phased steps, i.e.low- and high-pressure analyses.In the low-pressure analysis, the gases were evacuated from the penetrometer.After the evacuation, in the high-pressure analysis, themercury was injected into the pores as the pressure increases.Table 1 provides the detailed information about the AutoPore IV 9520,including the range of low-and high-pressure,pore diameter,and specimen size.The porosities of Berea and Otway sandstones are 17.4% ± 0.9% and 25% ± 1.9%, respectively (Cheon et al., 2017).Fig.2a shows a comparison of the pore size distribution of each sandstone.Most of the pore radius of the Berea sandstone is in the range of 5-10 μm, while that of the Otway sandstone shows a smaller value,and a lower volume ratio section exists between the small and large pores.

Table 1Information on the AutoPore IV 9250 for MIP test.

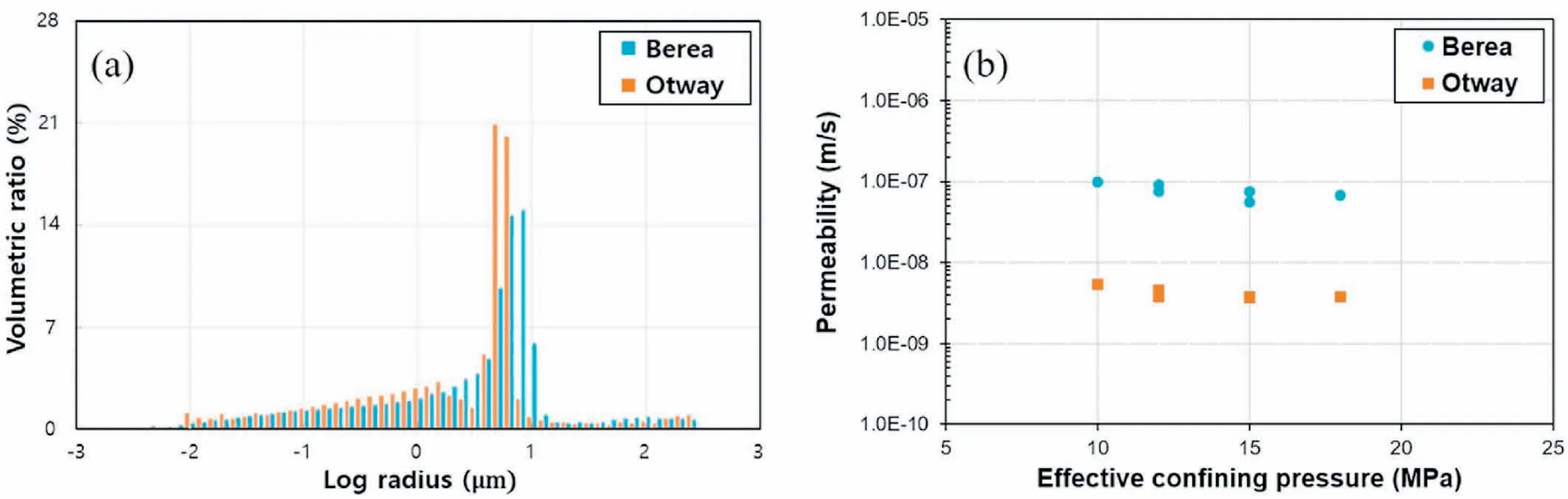
Fig.2.Comparison of pore size distributions (a) and permeability variation with increasing effective confining pressure (b) in both sandstones.

Fig.3.3D schematic diagram of pores and throats using the medial axis method(Takahashi et al., 2014).

Subsequently,we performed the flow pump test to measure the permeabilities at different confining pressures.The confining and pore pressures during the tests were adopted as a combination of(15 MPa, 6 MPa), (20 MPa, 8 MPa), (25 MPa, 10 MPa), (25 MPa,13 MPa), (30 MPa,12 MPa), and (30 MPa,15 MPa) to simulate the CO2geological storage conditions considering the capacity and characteristics of the testing system.The maximum confining pressure in the tests was determined considering the in situ stress at a depth of 1200 m.In the flow pump test, the diameter of thespecimen was 50 mm and the height was 25 mm.We measured the injecting pressure until the injecting water flow pressure reached a constant value at the downstream side.Although Otway sandstone has a larger porosity by approximately 7%-8%compared to that of the Berea sandstone (Fig.2a), its permeability is smaller by one order of magnitude (Fig.2b).

Fig.4.3D images of the medial axis in glass beads with diameters of 600 μm:(a)Original CT data,(b)pore space image extracted from CT data,(c)grain distribution,and(d)medial axis image obtained from pore network data (Takahashi et al., 2014).

Table 2Glass ball diameters and porosities obtained using microfocus X-ray CT processing.

Finally, we used an HMX225 X-ray CT system (TESCO Corporation) to characterize the geometrical information of void spaces.The maximum voltage of the system is 225 kV, and the focal spot size is 5 μm.The resolution of two-dimensional (2D) images is 1024 × 1024 pixels in this system, and the X-ray source is small enough to obtain a clear boundary image (Takahashi et al., 2006).The detailed results of the measurements are introduced in the following section.

3.Geometrical information on void spaces

3.1.Microfocus X-ray CT and 3DMA

The most appropriate procedure to focus on the pore structure and to qualify the pore space geometry in CT images is to set the threshold to match a predetermined porosity and bulk density.Lindquist and Venkatarangan (1999) provided the 3DMA package that can be used to investigate the geometries of pore and grain phases in 3D CT data, based on the Kriging algorithm to segment the voxel images.Fig.3 shows the medial axis behaviors of two nodal pores in two dimensions(Takahashi et al.,2014).The medial axes of a pore (or a sphere) and a cylinder are represented as a straight line through the center of the pore and the axis of rotational symmetry, respectively.The medial axis for any n-dimensional object can be defined by a “burning algorithm” (Lindquist et al., 1996).In this method, a pore is represented as a circle within the maximum void space,and a throat is defined as the local minimum of the cross-sectional area in each channel(Cheon et al.,2017).For instance,as illustrated in Fig.3,P1and P2are the adjacent pores,and the dashed lines are the medial axes through the center of the pores.The adjacent pores P1and P2are connected by throats,which are represented by dotted lines.

The medial axis is a network of paths and vertices for an object in a spatial continuum unless the object comprises embedded spaces where the medial axis also includes surface segments.When the object is digitized, the medial axis is composed of digitized paths,vertices and potential surfaces which correspond to a line of connected voxels, a cluster of one or more voxels, and a sheet of voxels,respectively.In a typical conceptual model,the void space is separated by nodal pores located at multi-grain junctions.In approximately equidimensional geometry, the pore channels join the nodal pores,and the nodal pores contain microcracks located at interfaces between adjacent grains and tubular pores along threegrain edges.Pore and throat analyses, including effective pore and throat radii,and pore and throat volumes,are analyzed by the special 3D porous/particle analysis software ExFACT.

To confirm the applicability of the 3DMA method to quartz grain aggregates,we measured the pore geometries of small packed glass balls with various diameters.Fig.4 is an example of the CT image and medial axis analysis for the packed glass balls with diameters of 600 μm(Takahashi et al.,2014).In Fig.4d,the closer the distance to the red color(6.34 μm),the narrower the pore space,and the closer the distance to the blue color(165.03 μm),the wider the pore space.We can visually confirm the relationship between the real magnitude of the void space and the medial axis expression based on different colors.Table 2 shows the porosities obtained using the image processing technique at various glass ball diameters.All of the calculated porosities range from 34%to 38%,and the geometry of glass beads exhibits tetragonal sphenoidal and cubical tetrahedral packing patterns under realistic packing conditions (Fig.4).The peak values are located approximately at 70-90 μm for pore radii and 60-70 μm for throat radii.The maximum pore radius attained was 270 μm, corresponding to the layer distance in the tetragonal sphenoidal packing pattern.We confirmed that 3DMA method is applicable for the geometrical evaluation of porous media.Various factors including flow channel, flow path and percolating backbone influence the medial axis.

Using these 3DMA data, we quantified the number of total pores, number of interior pores, number of throats, coordination number,number of connecting paths between two faces,tortuosity,and the shortest path distributions within arbitrary regions.It was found that the microfocus X-ray CT provides useful geometrical and spatial information about individual particles and voids as a nondestructive visualization tool.

3.2.Geometrical information

We obtained the extracted void spaces and transparent images from the original CT voxel images of 1 mm cubes in both sandstones, as shown in Fig.5 (Cheon et al., 2017).The distinction of pores and particles from CT images was performed using a twophase segmentation method based on bimodal histogram and the maximum likelihood thresholding method, which considers the effect of mixels (mixed pixels), for two-phase segmentation problems (Kato et al., 2013).As previously noted based on the total porosity determined by MIP, the Otway sandstone has an approximately 8% larger porosity and smaller dominant pore size than Berea sandstone.Fig.6 presents the 3D medial axis distributions of both sandstones, which shows an obvious difference.In Fig.6, the red color represents a narrow medial axis (3.66 μm), and the blue color indicates a wider medial axis (29.28 μm).Otway sandstone showed a more complex connection of the medial axes compared to that of the Berea sandstone,but the size of the medial axis for the Berea sandstone was relatively larger than that of the Otway sandstone.The result agreed well with the pore size distribution,as shown in Fig.2a.

Corresponding to the permeability measurement direction (Z-axis), we obtained geometrical information from the 3DMAs of 1 mm and 3 mm cubes.The effective pore and throat radii are the radii of an irregularly shaped sphere with the same pore and throat volumes.Fig.7 shows the comparisons of frequencies of effective pore and throat radii, coordination number, and effective throat/pore radius ratio of 1 mm and 3 mm cubes of Berea sandstone(Fig.7a, c, e and g) and Otway sandstone (Fig.7b, d, f and h).Converting the frequencies of pore and throat radii in the 1 mm cube to those in the 3 mm cube,i.e.multiplying the frequencies by 27,yields a result similar to those directly obtained from the 3 mm cube.

Fig.6.3D medial axis distributions of (a) Berea and (b) Otway sandstones.

The coordination number can be expressed as the number of grains surrounding a void space;therefore,a large number suggests that the void contacts many grains and throats.The effective throat/pore radius ratio is denoted as an average value,thus the higher the effective throat/pore radius ratio, the more similar the size of adjacent pores.If this ratio is small,large variations exist between adjacent pores.Fig.7e-h shows the coordination number and throat/pore radius ratio values.The frequencies in the 3 mm cube are higher than those in the converted 3 mm cube.Fig.8 shows the relationship between the coordination number and pore radius of Berea and Otway sandstones.In the case of the 3 mm cube,there is a high frequency of large pores in both sandstones,and the Otway sandstone exhibits a large coordination number and has a high frequency of larger pores.Thus we conclude that the correlation magnitude of the coordination number can reflect the total porosity difference.Fig.9 shows the calculated tortuosity distributions,and Tables 3 and 4 present the tortuosity of both sandstones.Compared to the results of the 1 mm cube,the tortuosity of the 3 mm cube and its differences in each direction decrease.

4.Discussion

In this section, we investigate the relation between the 3D geometrical information of void spaces and permeability differences of two sandstones.First, we discuss the total porosity difference.As shown in Fig.2a,the difference in the total porosities of Berea(17.4%)and Otway(25%)sandstones is approximately 7.6%,while the permeability of the Berea sandstone is one order of magnitude higher than that of the Otway sandstone (Fig.2b).The effect of the effective confining pressure on the permeability was almost the same for both sandstones.Table 5 provides the reservoir properties of various CO2storage projects with the information of rock type and coring depth.Fig.10 shows the relationship between the permeability and porosity.It can be observed from the figure that the permeability does not show an obvious relation with the porosity.

In this study,the size ranges of the two rock types are almost the same based on their pore size distributions,but the frequency of 1-10 μm pores is different.The frequency of 60-2000 μm pores is dominant in the Berea sandstone,while the frequency of 50-70 μm pores prevails in the Otway sandstone.This pattern can cause permeability difference between the two sandstones.From the total porosity and permeability differences, we can conclude that the correlation magnitude of the total porosity does not necessarily regulate the permeability.In general,we theorize that a larger total porosity in sandstone is correlated with higher permeability,while experimental observations differ from this conclusion.

The reason for the unusual relationship between the permeability and porosity might result from the void geometry.Fig.7g and h shows the effective throat/pore radius ratio in adjoining void spaces.A value of 1 indicates the same radii of pores and throats.The Otway sandstone exhibits a larger frequency at lower ratios, especially less than 0.3, compared to that of the Berea sandstone.The larger frequency at lower effective throat/pore radius ratios suggests that fluid flow in the Otway sandstone is characterized by dominant fluid energy loss due to repeated bottleneck effect, which means that fluid transports from large void spaces to relatively narrow spaces, or from small spaces to large void spaces.Katz and Thompson (1986) suggested that the porosity is not important for predicting the permeability.Meng(1994) investigated the relationship between the porosity and the permeability of sandstones, and reported that the permeability is decreased in direct proportion to the pore radius due to the obstruction of the flow induced by bottlenecks and surfaceroughness.Nelson (1994) stated that the permeability of sands and sandstones might increase with decreasing porosity because of the increase in coarse grain size content.Mosquera et al.(2000)performed a series of permeability tests on granitic rocks and observed that the permeability is reduced when the porosity is increased slightly.Mosquera et al.(2000) suggested that the increase in the proportion of the lowest pore size could affect the decrease of permeability.The experimental results of Otway and Berea sandstones in this study correspond well to the tendency of the previous studies, and the bottleneck effect might affect the energy loss during fluid flow.

Fig.7.Distributions of interior pore and throat radii,coordination number,and effective throat/pore radius ratio of Berea(a,c,e,g)and Otway(b,d,f,h)sandstones in 1 mm and 3 mm cubes.

Fig.8.Relationship between coordination number and effective pore radius of (a) Berea and (b) Otway sandstones in 1 mm and 3 mm cubes.

Fig.7a-d shows the frequencies of interior pore and throat distributions in both sandstones.The Otway sandstone has a higher frequency in the entire range;however,in the range of large pores,the relative difference in frequencies tends to decrease for the two sandstones.Fig.7e and f presents the distributions of coordinationnumber in both sandstones, from which we can consider that the larger the coordination number, the larger the void space.

Fig.9.Distribution of tortuosity in X-, Y-, and Z-directions of (a) Berea sandstone and (b) Otway sandstone in 1 mm and 3 mm cubes.

Table 3Tortuosity and number of connecting paths in 1 mm and 3 mm cubes of Berea sandstone.

Table 4Tortuosity and number of connecting paths in 1 mm and 3 mm cubes of Otway sandstone.

Table 5Reservoir properties of various CO2 storage projects.

Fig.11 shows the relationship between the tortuosity and channel volume of the shortest paths.The Berea sandstone exhibited higher tortuosity with lower channel volume.Because the tortuosity indicates the ratio between the length of a real path and the shortest geometrical length, higher tortuosity tends to suggest lower permeability.There were no significant features in the tortuosity between the two sandstones considering the geometrical information related to the permeability, and thus we cannot sufficiently extract direct correlations between permeability differences and 3D void geometries in the sandstones.

5.Conclusions

Fig.10.Relationship between permeability and porosity of various CO2 storage projects.

In this paper, a series of permeability tests and X-ray CT observations were conducted to clarify the relation between the permeability and the pore structure.The Otway sandstone exhibited a porosity that was approximately 7.6%higher than that of the Berea sandstone but displayed lower permeability by one order of magnitude based on the flow pump test.The phenomenon is unusual and differs from common sense in the engineering field.To obtain a good correlation of the permeability differences between the Berea and Otway sandstones, which have different porosities and 3D void geometries, the flow-relevant geometrical properties of void spaces in both sandstones were compared.

Based on the above analyses,the total porosity was not the main reason for the permeability difference.To clarify the unusual observation, pore structure was investigated using X-ray CT and MIP.A higher coordination number indicating that the void contacts with many grains and throats resulted in higher porosity.While tortuosity values could not represent the interpreted correlation magnitudes associated with permeability.However, the larger frequency at a lower effective throat/pore radius ratio of theOtway sandstone might cause lower permeability due to the fluid energy loss induced by repeated bottleneck effect, which means that fluid transports from large void spaces to relatively narrow spaces, or from small spaces to large void spaces.Therefore, low pore/throat ratios correlate with low permeability values in this study.

Fig.11.Relationship between tortuosity and channel volume in the Z-direction.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported by the Basic Research and Development Project of the Korea Institute of Geoscience and Mineral Resources (Grant No.20-3115).