Case study of a driven pile foundation in diatomaceous soil.I: Site characterization and engineering properties

Jiayao Wang, Ehsan Yazdani, T.Matthew Evans

School of Civil and Construction Engineering, Oregon State University, Corvallis, OR, 97331, USA

Keywords:Diatomaceous soil Problematic soil Site characterization Laboratory testing

ABSTRACT Diatomaceous soils are comprised of the silica frustules of diatom microalgae that are present in marine and lacustrine environments throughout the world.Owing to their unique origin,diatomaceous soils are typically characterized by high intraparticle porosity, complex particle shapes, and uniform mineralogy,causing them to exhibit atypical physical and engineering behaviors.A substantial deposit of diatomaceous silt was observed during site exploration for construction of the Buck Creek Bridge on OR140 near Klamath Falls, OR, USA.A comprehensive laboratory and in situ testing program indicated that the diatomaceous soil possessed “non-textbook” engineering properties.Specifically, tested samples had high liquid limits(≈100%-140%)with natural water contents at or near the liquid limit.Geologically,the soil is expected to be normally consolidated,yet high apparent overconsolidation ratios(OCR)(≈15-40)were observed both in oedometric consolidation tests and through cone penetration test (CPT) correlations.Standard penetration test (SPT) results show a corrected standard penetration resistance consistent with a medium-dense sand(i.e.(N1)60 ≈25).CPT results include corrected tip resistances(qt)of approximately 7-10 MPa and excess pore pressures(u2)of up to 4 MPa.In CPT dissipation tests,pore water pressures (PWPs) returned to hydrostatic pressure in less than 1 h.In this work, we synthesize these seemingly disparate material properties in an attempt to infer appropriate engineering properties for the diatomaceous deposit at the Buck Creek Bridge and attempt to provide insight into the underlying reasons for the observed behavior.

1.Introduction

Diatom is a type of unicellular microalgae found in both marine and lacustrine environments globally (Antonides, 1998).The diatom’s cell wall, called frustule, is comprised of hydrated silicon dioxide (SiO2·nH2O), which is effectively chemically inert in the presence of most chemicals found in the natural environment.Diatoms have a life-cycle on the order of one week, after which the algae decays,leaving behind the frustule(Franklin,2004).Because the remaining frustule was the diatom’s cell wall (effectively, an“exoskeleton”), it has high intraskeletal porosity after the algal material is decomposed (Tanaka and Locat,1999; Shiwakoti et al.,2002).A consequence of this unique con uence of factors within a given body of water is a continuous supply of environmentally persistent sediments having extremely high intraparticle porosity,thus resulting in deep deposits of materials with problematic(or,at least, uncertain) engineering properties.

The geotechnical behavior of diatomaceous soils has been extensively studied for lacustrine deposits in Mexico City (Díaz-Rodríguez et al., 1992; Díaz-Rodríguez and Santamarina, 2001;Díaz-Rodríguez, 2003, 2011) and marine deposits in Japan(Maekawa et al., 1991; Matsumoto et al., 1995; Shiwakoti et al.,2002; Locat et al., 2003; Hong et al., 2006) and Korea (Lee et al.,2011).These studies consistently found non-textbook geotechnical behavior for composite materials containing even small fractions of diatomaceous material.For example, soil mixtures of 20% diatom particles and 80% kaolin clay have been observed to have larger liquid and plastic limits than 100% kaolin clay (Tanaka and Locat, 1999; Shiwakoti et al., 2002; Sonyok, 2015), whereas addition of other similar-sized silica particles (e.g.sand) would be accompanied by decreases in liquid and plastic limits(Simpson and Evans, 2016).Small proportions of diatom particles in kaolin clay also cause increases in shear strength,dilation,and compressibilitythat are not observed with the addition of similar-sized conventional silica particles (Maekawa et al.,1991; Díaz-Rodríguez et al.,1992; Sonyok, 2015; Hong et al., 2006; Wiemer and Kopf, 2016).Wiemer and Kopf (2016) performed a series of cyclic triaxial tests and found that clayey-silt soils transition from cyclic softening behavior to liquefaction behavior at about 50%diatom content and that cyclic strength increases as diatom content increases.

These studies clearly indicated that standard geotechnical interpretations and correlations are not appropriate for soils containing even a small proportion of diatom particles.However,Evans and Moug(2020)noted that published literature addressing in situ test interpretation, geotechnical design procedures, and construction methods for diatomaceous soils is scarce.Nonetheless,if these unique and non-standard behaviors are not considered during design, unexpected engineering consequences will manifest.Construction on diatomaceous soils has resulted in high pile rebound(shallow refusal), piles that run long, and/or excessive postconstruction settlement.For example, excessive settlement after embankment construction was observed at Wickiup Junction, OR,USA (Cornforth Consultants, 2017) and a subaqueous landslide of diatomaceous deposits in South-Central Chile affected both onshore and offshore infrastructure, yet the slope failure mechanism was poorly understood (Wiemer et al., 2015).

In the current work, we consider the engineering behavior of a thick diatomaceous soil deposit in Klamath County, OR, USA(42°16′16.8456′N,121°29′2.1948′W, elevation of 1264.62 m).The deposit was encountered as part of the OR140 Buck Creek bridge replacement project.The geotechnical design called for two bents,each resting on seven closed-end pipe piles(United States standard 16-in (406-mm) diameter, 0.375-in (9.5-mm) wall thickness,PP16 0.375) (1 in ＝2.54 cm).The diatomaceous materials were characterized through a combination of in situ (e.g.standard penetration test(SPT),cone penetration test(CPT))and laboratory testing.Pile capacity was assessed using a pile driving analyzer(PDA) with CAPWAP analysis.

This article is the first of two companion papers on site characterization and pile installation for the Buck Creek Bridge replacement project.Herein, we discuss measurement of physical and engineering properties of the diatomaceous soils at the Buck Creek site.We seek to synthesize laboratory and in situ behaviors and correlate them to index properties.In the second of the companion papers(Yazdani et al.,2021),we discuss pile installation and capacity,specifically within the framework of PDA and CAPWAP.By documenting and disseminating such a comprehensive case study coupled with analysis and synthesis of data across multiple modes,we seek to advance the current understanding of the engineering behavior of diatomaceous soils and aid future researchers as they continue to explore this area of active research.

2.The unique behavior of diatomaceous soils

Diatomaceous soils exhibit broadly non-textbook behaviors when tested at the element scale ex-situ (Sonyok, 2015).Being largely comprised of hydrated silica (SiO2·nH2O), we expect that they would have a particularly active diffuse double layer,but they often hold more moisture than chemically active high-plasticity clays (Díaz-Rodríguez et al., 1998).While this high moistureholding capacity implies a low shear strength, the opposite is actually true: diatomaceous soils tend to exhibit relatively high shear strengths, likely due to their irregular particle shapes(Shiwakoti et al., 2002; Wiemer et al., 2017).

Fig.1.Four distinct types of porosity present in diatomaceous soils (after Locat et al.,2003).

Specific surface area and porosity are intimately related for diatomaceous soils due to the distinct types of porosity present in these materials.Tanaka and Locat (1999) identified four different pore families present in diatomaceous soils (Fig.1): (i) intraskeletal; (ii) skeletal; (iii) intra-aggregate; and (iv) interaggregate, listed in order of increasing size.Thus, porosity in diatomaceous soils exists at four different scales.At the smallest scale(intra-skeletal), the porosity is purely a function of the particle geometry(e.g.a perforated hollow cylinder,Fig.1).Specific surface area is often a good indicator of particle shape (e.g.platy versus spherical particles), but measurement of specific surface area in diatomaceous soils is not at all straightforward.In one example from the literature, dry measurements using nitrogen adsorption resulted in measured specific surface areas of 20-30 m2/g, while wet measurements on the same material using methylene blue produced results in the range of 65-110 m2/g (Lee et al., 2011;Palomino et al.,2011).Locat and Tanaka(2001),however,reported typical values of specific surface area for diatoms to be 10-20 m2/g.These findings indicate that while specific surface area is a fundamental parameter that provides significant insight into the engineering behavior of soils (Santamarina et al., 2001, 2002), it is particularly difficult to measure in diatomaceous soils, largely owing to their complex four-mode pore structures.

As a result of their large water-holding capacity, diatomaceous soils often have unusually high liquid limits (LL) and plasticity indices (PI) (Shiwakoti et al., 2002; Sonyok, 2015; Caicedo et al.,2018).This behavior is well documented in the literature with one striking example being the diatomaceous soils in Bogotá,Columbia,as reported by Caicedo et al.(2018).Colloquially,the soils are often termed “Bogotá clays” though, in fact, they are mostly silty.The confusion stems largely from the measured consistency limits: over 95% of 1024 tested soil samples had Atterberg limits that plot on or above the A-line,with many approaching the U-line.These results strongly imply a high-plasticity clay in the classic interpretive framework(e.g.Lambe and Whitman,1969),yet there are very few clay-sized(＜ 2 μm)particles and very high quartz(up to 50%) and feldspar (15%-42%) contents.

3.Site exploration and in situ testing

3.1.Overview

As shown in Fig.2,four boreholes were advanced at the site,two in 2016 (DH16-01 and DH16-02) and two in 2017 (DH17-01 and DH17-02).Three CPTs were performed,i.e.CPT-01,CPT-02,and CPT-03,in parallel with advancing the 2017 boreholes.In situ testing canbe used to infer the engineering properties of in-place soils,either with or without extraction of samples for laboratory testing.As part of borehole advancement, SPTs were performed and undisturbed samples were obtained for laboratory testing using Shelby tubes.Laboratory tests for physical characterization included Atterberg limits, natural water content, and grain size distribution.Engineering properties were measured in oedometric consolidation and triaxial compression tests.All subsurface penetrations were in the general vicinity of the planned pile installations for Bents 1 and 2.

Fig.2.Plan view of the Buck Creek Bridge site.Note that BaPb indicates “Bent a Pile b”.

Fig.3.Subsurface profiles from four borehole logs.

3.2.Standard penetration tests

Four boreholes were advanced near the pile installation locations, as shown in Fig.2.Boreholes DH16-01 and DH16-02 both started with 8-in O.D.hollow stem(HS) augers through the upper 1.83 m, consisting of asphalt and fill.Mud rotary techniques were then used to advance the boreholes to their final depths of approximately 30.94 m.Boreholes DH17-01 and DH17-02 were advanced to 18.5 m and 18.33 m, respectively, using mud rotary techniques.SPTs were performed approximately every 1.52 m in DH16-01 and DH16-02 and every 0.76 m in DH17-01 and DH17-02.Disturbed samples were obtained from each SPT.In addition to disturbed samples, eight undisturbed Shelby tube samples were obtained from boreholes DH17-0x.The subsurface profiles in each of the four boreholes are shown in Fig.3.Two distinct diatomaceous deposits are clearly evident from 4 to 31 m below ground surface(bgs),with a dense sand layer at approximately 17.5-19 m bgs separating them.

3.3.Cone penetration tests

Three CPTs were advanced near the boreholes and the pile installation locations are shown in Fig.2.The depths of the soundings were 4 m(CPT-01),16.25 m(CPT-02),and 18 m(CPT-03).We consider herein only CPT-02 and CPT-03 because CPT-01 did not penetrate the diatomaceous layer.The groundwater table was at 2.4 m in the borehole closest to CPT-02(DH17-01)and at 3 m in the borehole closest to CPT-03 (DH17-02).Dissipation tests were performed at multiple depths during testing to assess the hydrodynamic behavior of the soil.As the cone is advanced, excess pore water pressure (PWP) is generated.Penetration is arrested at certain depths to record pore pressure dissipation with time.The coefficient of consolidation and hydraulic conductivity can be inferred from the measurements (Wroth, 1984; Baligh and Levadoux, 1986).Unlike a laboratory oedometer test, which only allows vertical drainage, drainage occurs in all directions in adissipation test.Prior studies (Bjerrum and Johannessen,1961; Lo and Stermac,1965) showed that radial drainage plays a dominant role.

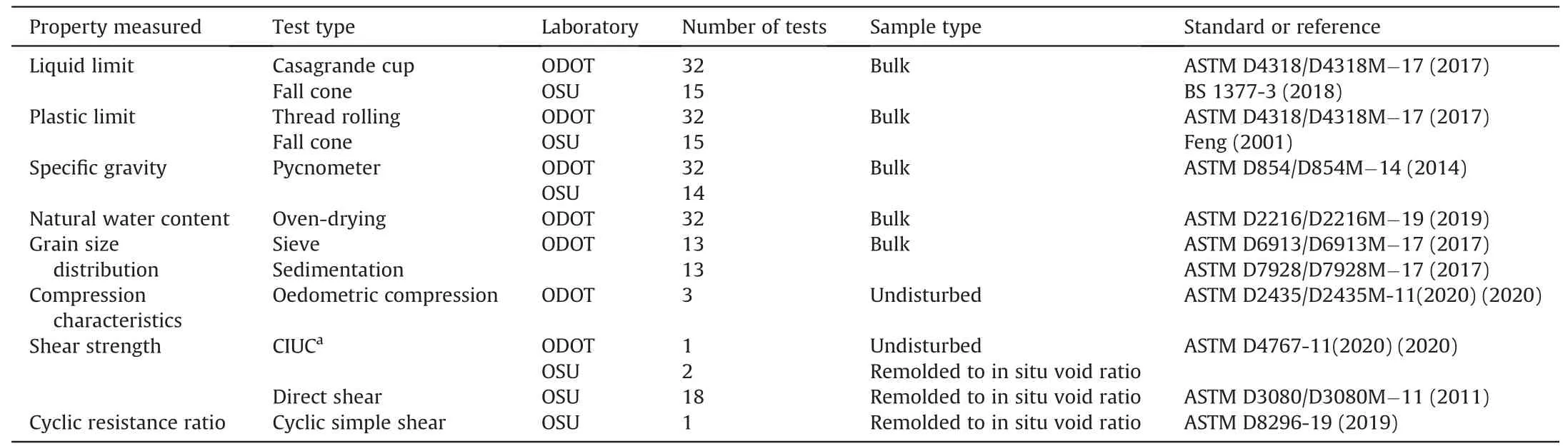
Table 1Summary of laboratory testing program.

Various approaches have been used to predict the coefficient of consolidation from pore pressure dissipation measurements.The solution proposed by Teh and Houlsby (1991) combines the strain path method and large strain finite elements to derive a dissipation model to obtain the distribution of PWP at various stages of dissipation.The horizontal coefficient of consolidation may be computed as follows:

where T*is the modified time factor(Teh and Houlsby,1991),chis the horizontal coefficient of consolidation, t is the time to various stages of dissipation,r is the radius of the cone,and Iris the rigidity index.

Burns and Mayne (1998) proposed a dissipation model via a combination of cavity expansion theory and critical state soil mechanics.The final predictive equation for the horizontal coefficient of consolidation is the same as Eq.(1),but the modified time factor T*is different from that of Teh and Houlsby (1991); rather, it is given as a function of effective stress friction angle (φ′) and overconsolidation ratio (OCR).Comparing the two definitions for the modified time factor,it may be observed that the T*recommended by Teh and Houlsby(1991)is generally higher than that from Burns and Mayne(1998).Indeed,Burns and Mayne(1998)reported 10－4T*1, while Teh and Houlsby (1991) suggested 0.038 T*1.6.In most cases,100%dissipation will not be fully achieved due to the time-consuming dissipation process, especially in low permeability soils(Krage et al.,2014).In this work,dissipation tests were terminated when the measured PWP was asymptotically approaching the hydrostatic pore pressure.

4.Laboratory testing program

A total of 71 split spoon samples were obtained for laboratory testing from the four boreholes: 15 from each of DH16-01 and DH16-02, 21 from DH17-01, and 20 from DH17-02.Eight undisturbed Shelby tube samples were obtained from DH17-01 and DH17-02, four from each borehole.The diatomaceous soils were tested in two laboratories: Oregon Department of Transportation(ODOT) and Oregon State University (OSU).The laboratory testing program is summarized in Table 1.In addition,samples from DH17-01 and DH17-02 were subjected to scanning electron microscope(SEM) imaging and energy dispersive X-ray spectroscopy (EDS)analysis at the OSU Electron Microscopy Facility.

5.Results and discussion

5.1.Material characterization

SEM images and results from EDS analyses of the diatomaceous materials are presented in Fig.4.Diatom frustules from a variety of species are visible in Fig.4a-c and representative chemical composition from EDS is shown in Fig.4d.High intraparticle porosity is evident in these images.The samples were found to consist primarily of silicon and oxygen (diatom frustules are composed of SiO2) with appreciable quantities of aluminum, calcium,and carbon.

The grain size distributions of 13 bulk samples were measured using sieve and hydrometer analyses.Previous studies (Shiwakoti et al., 2002; Díaz-Rodríguez, 2011; Lee, 2014; Sonyok, 2015;Wiemer and Kopf, 2016) have reported that the size of diatom particles generally varies from 1 μm to 100 μm,which is consistent with results from samples at Buck Creek (Fig.5).Clay-sized particles(＜ 2 μm)comprise approximately 15%-30%of the samples by mass and silt-sized particles (2 μm d ＜ 75 μm) comprise approximately 60%-75% of the samples by mass, where d is the particle size.Grain size distribution data were fit with a continuous function (Fredlund et al., 2000) to allow for ready calculation of descriptive particle sizes(i.e.d30,d50,and d60),which are presented in Table 2.Note that grain size distribution curve shape descriptors(i.e.coefficient of curvature(Cc)and uniformity coefficient(Cu))are not calculated because d10is unknown.

Large intraparticle porosity contributes to the high waterholding capacity of diatomaceous soils.Therefore, diatomaceous soils often exhibit unusually high liquid limits and plasticity indices.Test results from Buck Creek samples are presented in Fig.6 along with selected trends from the literature.Diatomaceous soils at the project site have liquid limits that vary over a relatively narrow range,with 114% LL 142%,while the plasticity index is somewhat more variable, 29% PI 75%.This results in a relationship between LL and PI that is less obviously linear than that for Bogotá clay(Caicedo et al.,2018)and also out-of-trend with results from 23 tests obtained from the literature (with coefficient of determination R2＝0.972).Atterberg limits were measured using two approaches: (1) Casagrande cup and thread rolling (ASTM D4318/D4318M－17, 2017); and (2) fall cone for LL (BS 1377-3,2018) and the Feng (2001)’s linear log10d-log10w approach for determining PL.The disparate clustering of Casagrande cup dataand fall cone data is notable and indicative of the difficulty of accurately measuring consistency limits on these complex materials.Generally, the fall cone approach results in slightly larger liquid limits and lower plasticity indices on average than the Casagrande method (see Table 3).There is also measurably morescatter in the fall cone measurements than in the Casagrande measurements.This is unusual because the fall cone is typically recognized as the more consistent of the two methods and may imply that the Casagrande cup is not the best method for measuring the liquid limit of high-porosity materials that are potentially prone to liquefaction under dynamic loading.Prior comparisons of Casagrande and fall cone measurements have indicated that the two methods generally have good agreement for LL up to about 120%(Wasti,1987)but the LL measured with the fall cone method is approximately 2%higher than that obtained by the hard base Casagrande cup (Di Matteo, 2012).Finally, unlike many diatomaceous soils reported in the literature which plot above the A-Line and approach the U-Line (high-plasticity clay), all of the Buck Creek results plot below the A-Line,indicating classification as a high-plasticity silt.

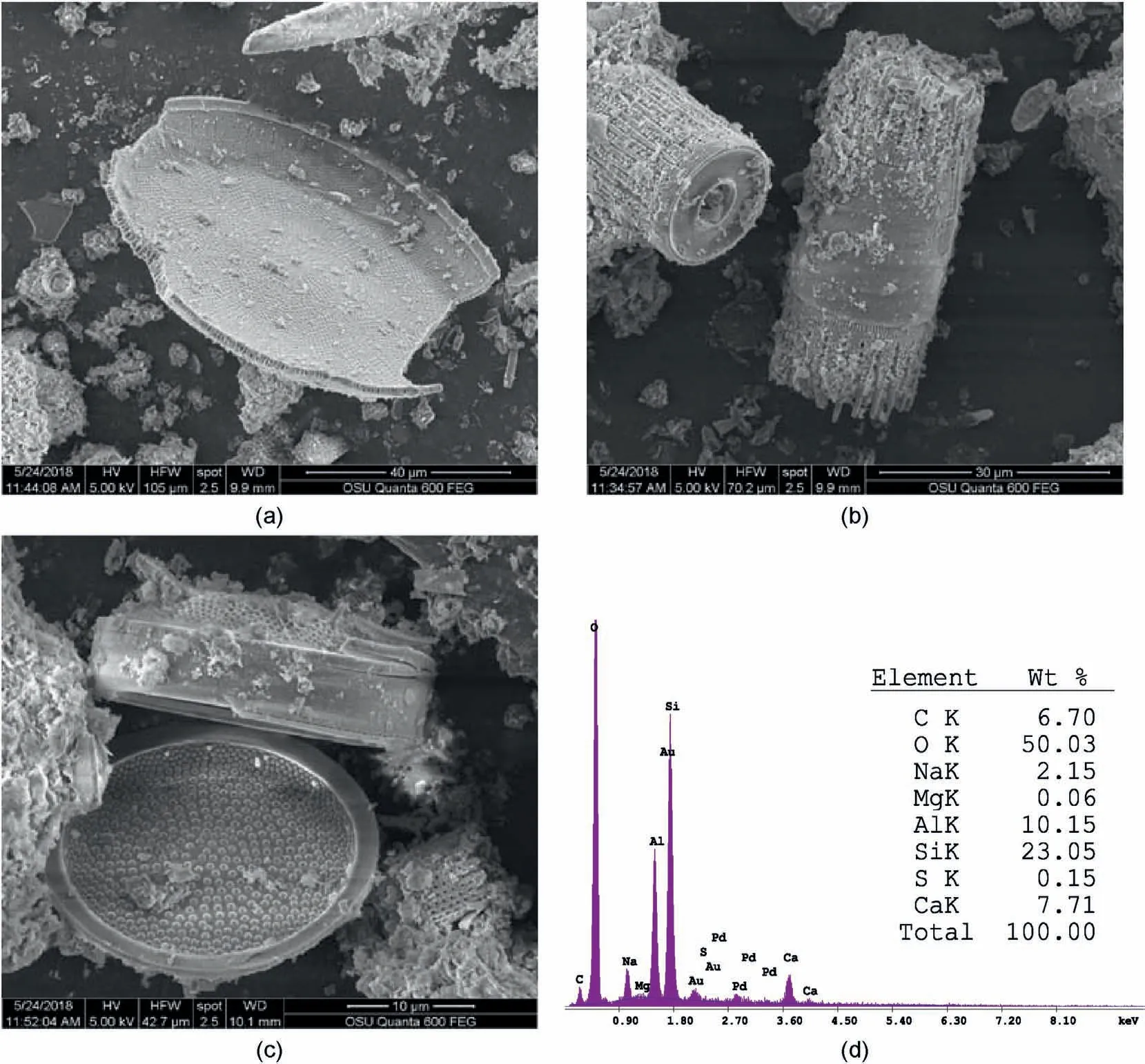
Fig.4.SEM images (a-c) and EDS results (d) from a sample of the diatomaceous silt.Note that the scale changes from (a) through (c).

Fig.5.Grain size distribution of samples obtained from DH17-01 and DH17-02.Measured hydrometer data were fit with the unimodal equation proposed by Fredlund et al.(2000) to indicate trends and similarities across samples.

Table 2Descriptive grain sizes for samples of Buck Creek diatomaceous soils.

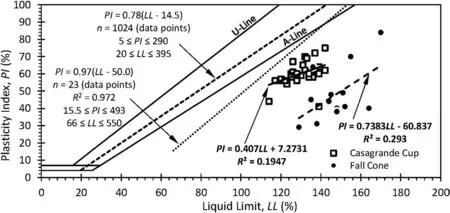
Fig.6.Plasticity of diatomaceous soils.Samples from Buck Creek were tested with the Casagrande cup and the fall cone.Caicedo et al.(2018) reported results from 1024 tests of Bogotá clay,and 23 additional samples from various locations were reported in the literature(Díaz-Rodríguez et al.,1992;2000;2009;Díaz-Rodríguez and Santamarina,1999;Díaz-Rodríguez, 2003; Su et al., 2004; Verdugo, 2008; Lee et al., 2011; Palomino et al., 2011; Zhang et al., 2013; Vera-Grunauer, 2014; AL Shatnawi and Bandini, 2018).

Table 3Average consistency limits as a function of test type.

The activity (A) of a soil is the ratio of the PI to the percent of clay-sized particles (defined as d ＜ 2 μm) in the matrix.Activity is typically considered to be approximately constant for a given clay mineral(Skempton,1953).Results from the Buck Creek site indicate 2 A 4 for the diatomaceous soils(Fig.7).Contrary to Skempton(1953)’s observation that activity increases with increasing clay fraction,the activity of diatomaceous soils tested here decreases as clay-sized fraction increases.We also note that the measured activity is generally lower than that reported for diatomaceous soils in Bogotá (Caicedo et al., 2018), Mexico City (Díaz-Rodríguez, 2011),and Japan (Shiwakoti et al., 2002).This implies differing diatom species,differing non-diatom soil components, or both.

The variations of physical characteristics(Atterberg limits,water content, specific gravity, and density)with depth through the diatomaceous deposits are presented in Fig.8.Atterberg limits and water content are observed to be relatively constant throughout the upper diatomaceous layer, indicating a consistent biology of the source organisms.Natural water contents wnare quite high(generally ＞100%) and typically near or above the LL.The specific gravity is significantly lower than those of other silicate soils (e.g.quartz sands) and lies generally in the range of 2.2 Gs2.6(Fig.8b).Due to low specific gravity and high void ratio, the unit weight of diatomaceous soils is appreciably lower than that of common soils(Fig.8c).The stiffness,strength,and compressibility of soils are stress-state-dependent, which highlights the significance of unit weight on the engineering response of the entire deposit.

5.2.Compressibility

Incremental load consolidation tests were performed on three undisturbed samples of diatomaceous silt and void ratio (e) vs.vertical effective stress () curves are presented in Fig.9 with a summary of the results presented in Table 4.Preconsolidation stresses were determined using the strain-energy method (Becker et al.,1987).The computed preconsolidation stresses are all quite high, resulting in an implied OCR 20, but there is no geologic justification for shallow,relatively recent(likely late Pleistocene to early Holocene),lacustrine deposits to be heavily overconsolidated.Thus, the high apparent preconsolidation stresses may be attributable to the phenomenon known as quasi-preconsolidation(Leonards and Ramiah, 1960; Bjerrum, 1967; Ma et al., 2014).Quasi-preconsolidation is the result of delayed compression (i.e.compression under constant effective stress)and usually occurs in clays.Consider, for example, the conditions illustrated in Fig.10, a soil deposit exists at a constant vertical effective stress of σ′0 for some(geologic)time.Due to delayed compression,the void ratio of the soil decreases from the initial void ratio e0to e1at a constant stress state.If the soil is then subjected to an incremental load consolidation test, “Curve b” will be measured, exhibiting an apparent preconsolidation stress ofeven though the vertical effective stress remains unchanged at.Bjerrum(1967)attributed delayed compression to the inability of soil voids (i.e.the pore water) to retard the compression (i.e.a lack of primary consolidation).Given their large porosity and high compressibility, diatomaceous soils may be particularly susceptible to quasipreconsolidation, though this requires further study.

Fig.7.(a) Activity chart for the diatomaceous silt; and (b) Variation of activity with clay-sized fraction.

Fig.8.(a)Consistency limits,(b)unit weight and(c)specific gravity as a function of depth.Consistency limits were measured using both the ASTM standard(REF)and the fall cone(FC) approach (REF).Specific gravity was measured independently in two laboratories: Oregon Department of Transportation (ODOT) and Oregon State University (OSU).

There are numerous reports of apparent preconsolidation of diatomaceous soils in the literature.Wiemer et al.(2017)observed a marked yield stress even in samples that were reconstituted at their liquid limit.They attributed this to the high permeability of diatomaceous soils at low overburden stresses, which was consistent with the findings of Pittenger et al.(1989).Several researchers(e.g.Day, 1995; Hong et al., 2006; Wiemer et al., 2017) have hypothesized that considerable particle crushing occurs during loading, even before an apparent yield stress, while others (e.g.Tanaka and Locat, 1999; Verdugo, 2008) observed little-to-no particle crushing in one-dimensional(1D)loading.In some cases,a relatively rigid response has been observed prior to a well-defined breakdown stress,which was attributed to diagenetic cementation or strongly interlocking fabric by some researchers (Tanaka and Locat, 1999; Hong et al., 2006).Clearly, the overall consolidation behavior of diatomaceous soil is not yet well understood.

The stress-state-dependent coefficient of consolidation (cv)describes the rate at which excess pore pressures dissipate after the change in total stress.Time-deformation data were recorded at each step of the incremental-load consolidation tests for the purpose of computing cvusing Terzaghi’s 1D consolidation theory(Terzaghi,1943).The most widely adopted methods for evaluation of cvare the so-called “log time”(Casagrande and Fadum,1940)and“root time”methods(Taylor,1948).These methods were developed before the democratization of scientific computing to allow researchers and engineers use approximations to compute cvusing hard-copy plotted data and hand calculations.Furthermore, both methods introduce undesirable subjective interpretations in the process.A more robust approach is to describe the entire timedeformation data series with Terzaghi’s solution to the 1D consolidation equation(Bardet,1997),in which cvemerges as a parameter of the minimization (i.e.a “fitting parameter”).However, in the method proposed by Bardet (1997), secondary compression is neglected,and in the Barros and Pinto(2008)’s approach,the user must select the time at which secondary compression begins,which is effectively unknowable.If Taylor(1948)’s assumption that secondary compression does not begin until at least 90%of primary consolidation has occurred, then the regression may be reformulated as a linear programming problem, stated as follows:

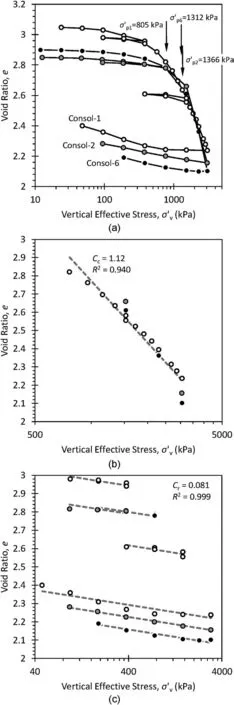
Fig.9.(a)Complete consolidation curves from all three oedometric compression tests.Preconsolidation stresses were calculated using the Becker et al.(1987)’s strain energy method.(b) Isolated virgin compression data and the best-fit line with compression index indicated.(c) Unload-reload data and corresponding best-fit lines.Regression was performed by enforcing a constant slope (the recompression index) across all lines.Consol-1 represents sample from DH17-01 at the depth of 4.57-4.8 m, Consol-2 represents sample from DH17-01 at the depth of 9.14-9.53 m,and Consol-6 represents sample from DH17-02 at the depth of 4.57-4.91 m.

Table 4Summary of results from oedometer consolidation tests.

where δ（t） and U（t） are the displacement and average degree of consolidation as a function of time,respectively;λk∈{cv,cα,δ0,δ100,TBoS} are the optimization parameters; δ0is the initial instantaneous settlement; δ100is the total primary consolidation settlement; Hdis the average drainage path length over the load increment;cα is the coefficient of secondary compression;H is the sample height at the beginning of secondary compression;t0is the time when the linear-log10t secondary compression model is assumed to begin; and TBoS＝ cvt／H2dis the dimensionless time factor corresponding to the beginning of secondary compression.The linear programming problem can be solved using the wellknown Karush-Kuhn-Tucker conditions (Karush, 1939; Kuhn and Tucker, 1951), a generalized Lagrangian multiplier approach that introduces complimentary slackness to accommodate inequality constraints.Nonetheless, we forego the elegance of such a tactic here and instead perform a standard least squares regression to the same end.

An obvious difficulty with fitting the measured data is the fact that the sum in Eq.(4)is infinite.To assess the implications of this fact,we replace the upper bound of the sum with a variable M equal to the number of terms in the summation.By inspection,it is clear that the sum will converge more rapidly for larger values of the dimensionless time factor,Tv＝ cvt／H2dand require more terms for small values of Tv.Fig.11 presents the average degree of consolidation as a function of M terms in the summation normalized by average degree of consolidation computed with 10,000 terms in the summation for very small values of the dimensionless time factor(i.e.for average degrees of consolidation of approximately 1.1%,3.6%,11%,and 36%).Clearly,the sum converges for very small values of M.We use 1000 terms for the optimization calculations.

Coefficients of consolidation computed using the above approaches are summarized as a function of applied vertical effective stress in Fig.12.On the virgin compression line (VCL), we observe that coefficient of consolidation generally decreases with increasing load as expected.Interestingly, however, values from inside the yield surface (i.e.on unload-reload loops) show an apparent generally increasing trend with increasing applied stress.The coefficient of consolidation is effectively the ratio of hydraulic conductivity to compressibility.It appears then that hydraulicconductivity is “recovering” during unload-reload cycles while elastic stiffness is not,implying very little elastic deformation when the yield surface is engaged,and thus,little elastic rebound during unloading (equivalently, a high Cc／Crratio, which is equal to 14 in our case).While this suggests particle breakage that creates a bracing network of fines and subsequent relaxation of the coarser load-bearing network,this has not been confirmed experimentally.

Fig.10.A schematic illustration of the quasi-preconsolidation effect (Bjerrum,1967).

We note here that there are a varying number of points for each sample and cycle on Fig.12; specifically, there is not a one-to-one correspondence between data points in Figs.9a and 12.This is due to the fact that many of the load steps did not exhibit classically bimodal “Terzaghian” deformation-time behavior (Sonyok, 2015),resulting in dubious fitting parameters and unrealistic values for the coefficients of consolidation and secondary compression.

5.3.Cyclic simple shear

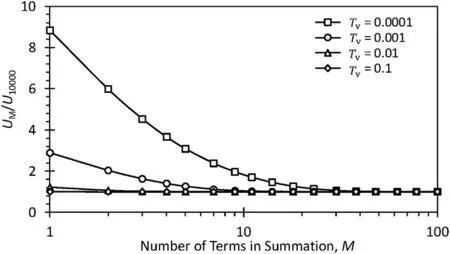
Fig.11.The sensitivity of average degree of consolidation calculations to the number of terms in Eq.(4).

There is very little data in the literature on the cyclic response of diatomaceous soils.Thus, to study the response of Buck Creek diatomaceous silt to dynamic loading, several undrained cyclic simple shear tests were performed on remolded diatomaceous samples to investigate the liquefaction resistance (cyclic resistance ratio, CRR).Samples were slurry consolidated and constant volume conditions were used to enforce undrained response (Finn and Vaid,1977).In this scenario, reduction in vertical stress is equivalent to the excess PWP that is developed in the samples under truly undrained conditions with direct measuring of PWP (i.e.constant load).Stresscontrolled tests were performed under 100 kPa of vertical stress and 7% double amplitude shear strain was considered as the liquefaction criterion.Fig.13 presents the relationship between the cyclic stress ratio (CSR) and the number of cycles to liquefaction (NL).Remolded Buck Creek diatomaceous silt has a CRRNL＝15of 0.22.The relationship between CSR and NLhas a slope of－0.153 on a log-log plot, consistent with the average value of －0.135 reported by Boulanger and Idriss(2004)for a collection of seven remolded clays and mine tailings.Interestingly, however, the average cyclic shear strength at 15 cycles was much higher for the clays and tailings(0.92)than that for the diatomaceous soil considered herein.

5.4.SPT profiles

Relatively few SPT results for diatomaceous soils are presented in the literature,but in sum,it has been consistently observed that unconsolidated diatomaceous soils are characterized by low blow counts(N 10 in most cases).Four boreholes were advanced at the Buck Creek site (Fig.2).Normalized energy-corrected blow counts for the SPTs in each hole were calculated as follows and are presented in Fig.14:

where CEis the factor of energy ratio,taken here as 1 in the absence of measured hammer energy; CBis the borehole diameter correction factor, equal to 1.15 here; CSis the sampling method factor,equal to 1 here; CRis the rod length correction factor and varies with depth; and CNis the correction for overburden effects,expressed as1.5, whereis the in situ vertical effective stress and patmis the atmospheric pressure.

The boreholes were terminated at approximately 18 m in DH17-01 and DH17-02 in a very dense soil layer and at approximately 30 m for DH16-01 and DH16-02.We observe that, in terms of corrected blow counts, both diatomaceous layers are remarkably uniform from 4 m bgs to 31 m bgs except for a very dense sand layer at approximately 18 m bgs (Fig.3).Average corrected blow counts for the diatomaceous deposits at Buck Creek are approximately（N1）60≈30 in all four boreholes, which is higher than many SPT results reported in the literature.

I got it. I got the joy, the sharing, the love. My dad pulled me to him in a warm embrace and just helds me for what seemed the longest time. We both cried.

5.5.CPT profiles and behavioral classifications

There are several reports of CPT in diatomaceous soils in the literature,but the coverage is far from comprehensive.Typical cone tip resistances reported in the literature are approximately 0.05-0.2 MPa (Díaz-Rodríguez et al.,1998; Díaz-Rodríguez, 2003), indicating extremely soft soil.Three CPTs were performed at Buck Creek Bridge(Fig.2).The first sounding,CPT-01,was terminated at the interface of the overlying fill layer and the top of the upper diatomaceous deposit, which is not considered herein.Soundings CPT-02 and CPT-03 were advanced to 16.25 m bgs and 18 m bgs,respectively;profiles of corrected tip resistance,sleeve friction,and excess PWP are presented in Fig.15.Approximate average hydrostatic pressure between the two soundings is shown.Note that all values are plotted in MPa.Unlike previous studies indicating a very soft soil, the cone tip resistances are always greater than 1 MPa in the diatomaceous layers.Spikes in cone tip resistance occurred at depths of 4.5-5.5 m and 10-12 m, which are consistent with SPT results (Fig.14).The groundwater table is at a depth ofapproximately 2.4-2.9 m (it varies between boreholes) and the interface between the upper sand/fill layer and the diatomaceous layer is at approximately 4 m.Very high excess PWPs were observed throughout the diatomaceous soil layers.

Fig.12.Summary of cv from oedometer consolidation tests.OC: overconsolidated;VCL: virgin compression line.

Fig.13.Results of cyclic simple shear tests.

Normalized cone measurements may be used to classify soils based on their perceived in situ engineering behavior,in contrast to ex-situ classifications based on measurements of mechanical properties (Robertson, 1990).Specifically, normalized corrected cone tip resistance (Qt), normalized sleeve friction (FN), and normalized pore pressure ratio(Bq)may be used to identify the soil classification:

where qcis the measured cone tip resistance,a is the cone area ratio(＝0.8 for the cone used at Buck Creek Bridge), u2is the penetration pore pressure, σv0is the total vertical stress, and u0is the hydrostatic pore pressure.Results from the CPTs are presented on the Robertson (1990)’s soil behavior type (SBT) classification chart in Fig.16.Based on the SBT charts, the diatomaceous soils plot largely in Zones 4 and 5,indicating silt mixtures and sand mixtures.We note here that diatomaceous soils have the gradation of silt but the mineralogy of sand.

Fig.14.SPT results of four borehole logs.

An appreciable number of measurements are located in Zones 8 and 9 in Fig.16a and outside the zone of applicability in Fig.16b.Behaviorally, these soils are classified as “very stiff sand to clayey sand”and “very stiff fine-grained”.These particular measurements occur primarily at the top of the diatomaceous layer.Mechanically,this can be explained by the fact that both normalized variables(Qtand FN)are functions of overburden stress(effective and/or total)to one degree or another and thus, are larger at smaller applied stresses.The large normalized pore pressure ratios (Bq) are re ective of the high excess pore pressures induced during penetration.In addition, CPT data have also been plotted on Schneider et al.(2008)’s SBT classification chart (Fig.17).Unlike Robertson(1990)’s SBT classification, Schneider et al.(2008)’s SBT classification focuses on more precisely interpreting OCR of soils by eliminating the in uence of qtfrom Bq(Fig.16b).Therefore,the trends of OCR will go on a different direction(Fig.17).In Fig.17,the majority of data points are located in where the excess pore pressure is excessively high, implying high OCR.Schneider et al.(2008)’s SBT classification is used to separate clay behavior, whereas Robertson(1990)’s SBT classification is used to identify soil type.

5.6.Results from CPT dissipation tests

The horizontal coefficients of consolidation were calculated at discrete depths from the CPT dissipation tests using the methods of Teh and Houlsby (1991) and Burns and Mayne (1998).In applying the Burns and Mayne (1998) method, two conditions were considered: OCR ＝1 based on the assumption that the soil is normally consolidated and that apparent OCR may be effectively calculated from CPT results.Eight dissipation tests were performed in the diatomaceous silt layer in CPT-02 and CPT-03.Vertical(fromoedometer tests) and horizontal (from CPT) coefficients of consolidation are presented in Fig.18.Teh and Houlsby(1991)calculated the horizontal coefficient of consolidation at four discrete times during dissipation and at normalized pore pressures of 0.2,0.4,0.6,and 0.8, where normalized pore pressure,unor, is given by

Fig.15.Profiles of (a) corrected tip resistance, (b) sleeve friction, and (c) excess PWP from CPT-02 and CPT-03.Approximate average hydrostatic pressure between the two soundings is shown.Note that all values are plotted in MPa.

where u is the pore pressure at time t, and uiis the initial excess pore pressure measured.As the normalized pore pressure increases,the coefficient of consolidation increases in both methods.A higher coefficient of consolidation is obtained for OCR ＞1 in that the time factor (T*) is greater for larger OCR.While there is significant spread in the values of cvand ch,there is no clear trend in variation with depth and no obvious distinction between the horizontal and vertical values.

5.7.Variation of engineering properties with depth

Soil engineering properties such as stress history (OCR), undrained shear strength (su), and effective stress friction angle (φ′)may be determined from both laboratory and in situ tests.Shear strength and stress history are empirically correlated to N as follows (Kulhawy and Mayne,1990; Mayne et al., 2001):

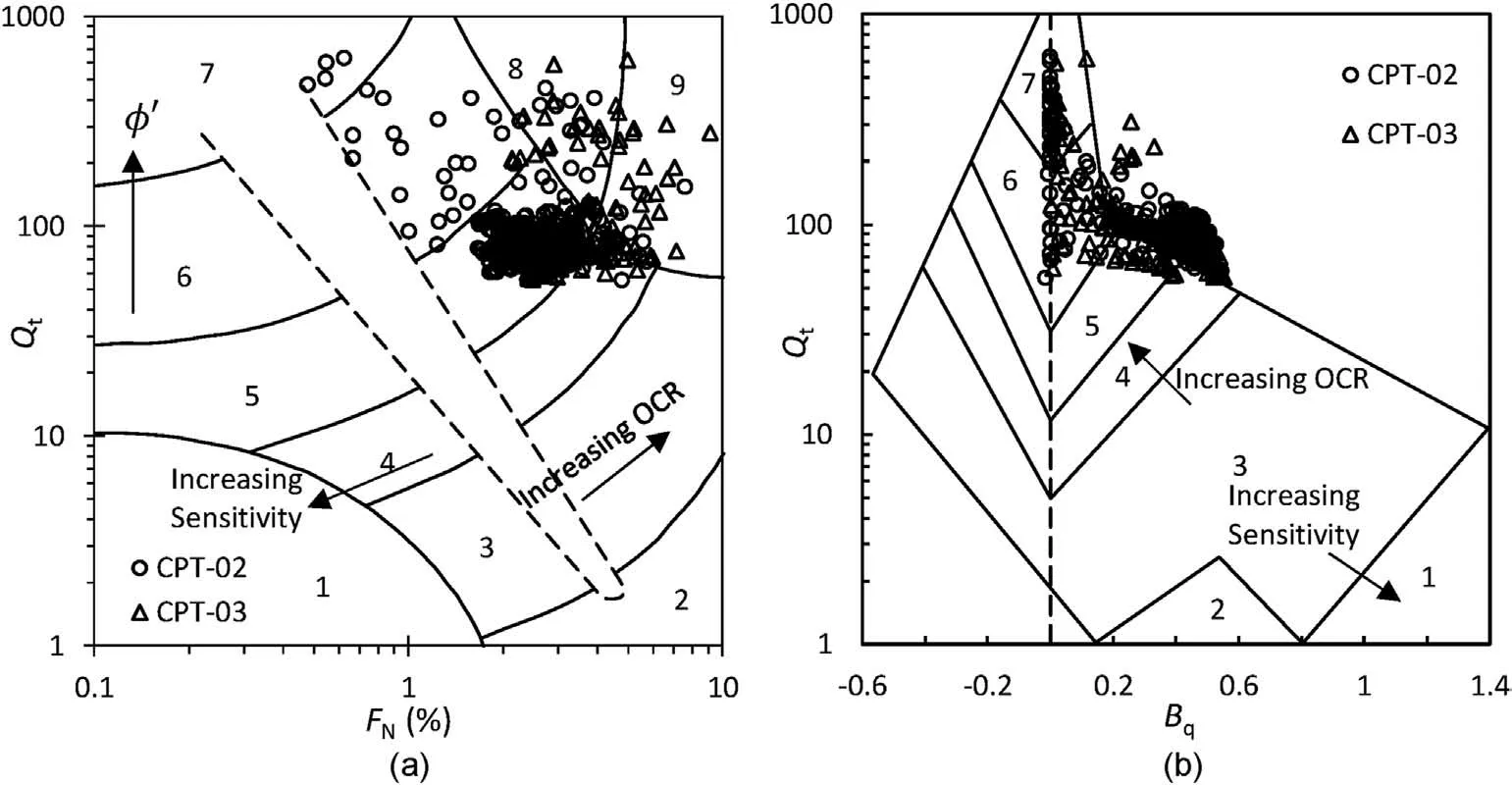
Fig.16.Soil behavior type classification chart based on normalized CPT data using(a)normalized friction ratio FN and(b)pore pressure parameter Bq.1.Sensitive,fine-grained;2.Organic soils-peats;3.Clays-clay to silty clay;4.Silt mixtures-clayey silt to silty clay;5.Sand mixtures-silty sand to sandy silt;6.Sands-clean sands to silty sands;7.Gravelly sand to sand; 8.Very stiff sand to clayey sand; 9.Very stiff fine-grained.

Similarly, it is possible to calculate stress history and strength parameters from CPT results (Mayne, 2007, 2014; Ouyang and Mayne, 2009).CPT correlations have the advantage that, while still somewhat empirical, they are often founded in sound theory,such as critical state soil mechanics and/or cavity expansion.In addition, the CPT collects three independent measurements (tip resistance, sleeve friction, and pore pressure), whereas the SPT is reliant upon blow count alone.In the current work, we calculate engineering properties from CPT results as follows:

Fig.17.Soil behavior type classification based on Schneider et al.(2008, 2012) SBT charts, where qcnet is the net cone tip resistance, calculated as qcnet ＝ qt－ σv0.

where Icis the CPT material index, Fris the normalized friction ratio,and Λ is computed as 0.93 for diatomaceous soils(see Fig.9)and assumed to be 0.8 for other soils (Mayne, 2007).Finally, it is possible to correlate shear strength to physical properties (e.g.consistency limits)based on results from other diatomaceous soils published in the literature (Caicedo et al.,2018):

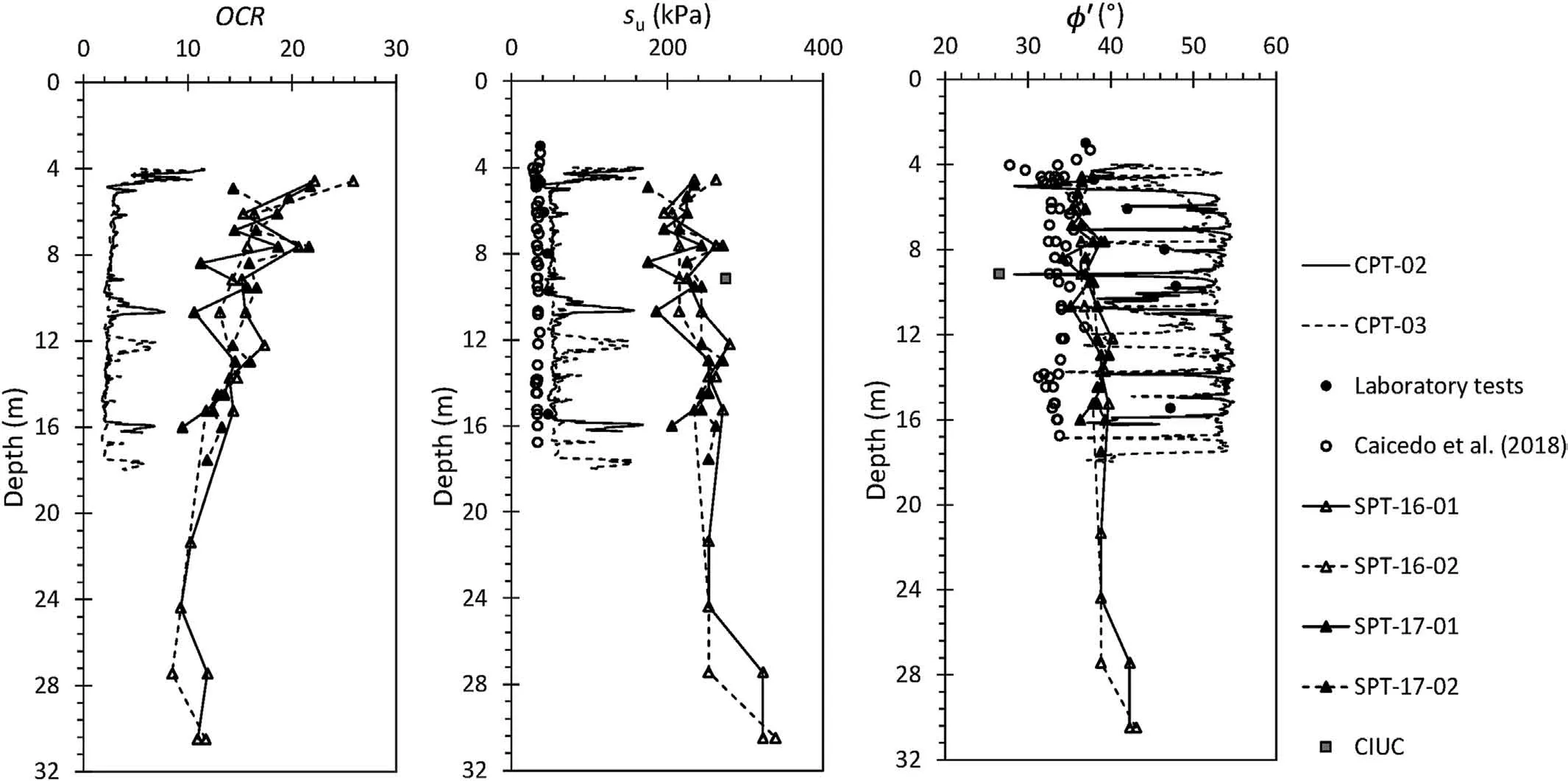
Fig.19.Friction angle along depth from different sources.

where w is the water content.For comparison, profiles of engineering properties determined using each of the aforementioned approaches are presented in Fig.19.

In comparison with the friction angles evaluated using these approaches, it is clear that the empirical correlation to liquid limit consistently predicts the lowest friction angle, at around 30°.CPT measurements imply the highest friction angles,up to 70°,though it is unlikely that the diatomaceous soils would exhibit such strength when subjected to design loads.Laboratory tests and SPT correlations show that friction angles are in the range of 40°-50°,which seem more reasonable based on previously published results.Note that the friction angles reported from direct shear tests were based upon tests on samples remolded to in situ void ratio and may not be identically equivalent to the mobilized in situ strength.However, we expect that the general stress-strain and critical state responses to nonetheless be qualitatively representative of in situ conditions.Note here that the friction angles predicted from liquid limits are fully-softened (i.e.critical state)friction angles that neglect structure and dilation, while those computed from CPT and SPT results will be more closely related to the peak friction angles.This is clearly shown in Fig.19 where the strengths predicted using the relationships of Caicedo et al.(2018)are consistently lower than those predicted from SPT and CPT.

CPT and SPT results both also predict high values of undrained strength and yield stress (OCR).This is consistent with laboratory results and results presented in the literature.Undrained shear strengthvalues predicted by SPTs mayappearunrealistically high,but they are consistent with results from a consolidated undrained triaxial test which indicted an undrained shear strength of approximately 300 kPa.These results further substantiate the conclusion that diatomaceous soils are not amenable to traditional interpretations based upon observations of the behavior of other “typical”soils.

6.Conclusions

The diatomaceous deposits at the Buck Creek Bridge site were characterized using both laboratory and in situ methods.Four boreholes and three cone penetration soundings were advanced in the vicinity of the new bridge foundation.Boreholes were advanced up to 30 m.The soil profiles show that diatomaceous soils begin approximately 4 m bgs and a thin(around 1 m)sand layer appears around 18 m bgs.Index testing on the diatomaceous soils indicated particle sizes that were nearly 100% passing the No.200 sieve,liquid limits in the general range of 100%-160%, and plasticity indices in the range of 40%-70%.The deposits were classified as high-plasticity silt.Natural water contents were typically near (or above) the liquid limit.SEM and EDS analyses indicated complex particle shapes with high intraparticle porosity and a mineralogy dominated by silicon and oxygen.

Oedometric compression tests and correlations from in situ tests indicated high apparent OCRs,even in the absence of confirmatory geologic data.This is consistent with previously published data,some of which indicated overconsolidation in samples of diatomaceous soils prepared from slurry.The OCRs observed in the Buck Creek soils ranged from 10 to 40.Coefficients of consolidation were high overall for such a fine-grained material, likely owing to the high porosity of diatomaceous soil.The coefficients of consolidation increased with applied load, indicating that compressibility was decreasing more rapidly than conductivity.

A variety of approaches have been used to assess the shear strength of the diatomaceous soils at the Buck Creek Bridge site.We consider results from empirical predictions based on consistency limits (i.e.fully-softened strength), in situ tests(SPT and CPT), and laboratory tests on undisturbed (triaxial) and remolded (direct shear)samples.While the various predictions certainly show some variation, they are all internally consistent, that is, they tell a coherent story.This indicates that,while diatomaceous soils do notbehave like most other geologic materials, their engineering properties do not defy characterization.

As is often the case with diatomaceous soils, the Buck Creek deposit exhibited unusually high shear strength given its high porosity, plasticity, and compressibility.This is typically attributed to particle interlocking between the irregular diatomaceous grains.Prediction of undrained shear strength from effective stress friction angle using a critical state approach implies high undrained shear strength, but less than that predicted from SPTs.

This study details site exploration and material characterization at the Buck Creek Bridge site.Thick (～27 m) deposits of diatomaceous soils were encountered during site exploration.Subsequently, installation of the design-required closed-end steel pipe piles proved difficult, while site conditions - when interpreted within a classical soil mechanics framework-implied that should not be the case.In the companion article to this work, pile installation efforts are detailed.The results of PDA tests are presented and the soil properties presented herein are interpreted within an engineering design framework.

Declaration of competing interest

The authors wish to confirm that there are no known con icts of interests associated with this publication and there has been no significant financial support for this work that could have in uenced its outcome.

Acknowledgments

This work was funded by the Oregon Department of Transportation (ODOT), which is gratefully acknowledged.The authors would also like to thank Kira Glover-Cutter,Brad Hayes,and Susan Ortiz, from ODOT, for providing us with their data and for many interesting discussions on the specific behavior of diatomaceous soils.