Numerical modeling for rockbursts: A state-of-the-art review

Jun Wng, Derek B.Apel,*, Yunyun Pu, Roert Hll, Chong Wei,Mohmmdli Sepehri

a School of Mining and Petroleum Engineering, University of Alberta, Edmonton, Alberta, T6G 2R3, Canada

b State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing, 400044, China

Keywords:Rockburst Numerical modeling Rockburst mechanism Dynamic modeling

ABSTRACT As the depth of excavation increases, rockburst becomes one of the most serious geological hazards damaging equipment and facilities and even causing fatalities in mining and civil engineering.This has forced researchers worldwide to identify different methods to investigate rockburst-related problems.However, some problems, such as the mechanisms and the prediction of rockbursts, continue to be studied because rockburst is a very complicated phenomenon influenced by the uncertainty and complexity in geological conditions, in situ stresses, induced stresses, etc.Numerical modeling is a widely used method for investigating rockbursts.To date,great achievements have been made owing to the rapid development of information technology (IT) and computer equipment.Hence, it is necessary and meaningful to conduct a review of the current state of the studies for rockburst numerical modeling.In this paper, the categories and the origin of different numerical approaches employed in modeling rockbursts are reviewed and the current usage of various numerical modeling approaches is investigated by a literature research.Later, a state-of-the-art review is implemented to investigate the application of numerical modeling in the mechanism study, and prediction and prevention of rockbursts.The main achievements and problems are highlighted.Finally, this paper discusses the limitations and the future research of numerical modeling for rockbursts.An approach is proposed to provide researchers with a systematic and reasonable numerical modeling framework.

1.Introduction

With the increasing demand for mineral resources and the continuous consumption of shallow mineral resources,the mining depth in the world is going deeper (Feng et al., 2019a).Some geotechnical engineering projects (e.g.tunnels and underground laboratories) are constructed in very deep areas with complicated ground conditions (Jiang et al., 2010; Zhang et al., 2012a).The ultimately high in situ stress and complex geological environment cause a series of geological hazards such as rockburst, rock mass caving, large deformation of excavations, and high ground temperature (Palei and Das, 2009; Fall et al., 2010; Xie et al., 2015; Yu et al., 2015; Ranjith et al., 2017; Shi et al., 2020).Rockburst is a dynamic rock failure phenomenon usually marked by sudden ejection of rock blocks from an underground opening.The ejection of the rock material is violent and associated with a rapid release of energy.Due to its unpredictability and high intensity, rockburst is one of the most hazardous geological disasters.It damages equipment,facilities and even causes fatalities, as shown in Fig.1.

Generally, rockbursts can be classified into three types: strainburst, pillar burst, and fault-slip burst according to the source mechanism (Hedley, 1992; Kaiser and Cai, 2012; Cai, 2013).Strainburst is the most common type of rockburst in all underground excavations(Zhang et al.,2012a;Cai,2013).It occurs due to the concentration of excavation-induced tangential stress and the existence of a relatively “soft” loading environment in the rock mass surrounding the fractured rock (Kaiser and Cai, 2012).The rock can fail locally at excavation boundaries in an unstable and violent manner.Pillar burst is a violent failure in the pillar core or the complete collapse of a pillar.This type of failure will occur suddenly when the accumulated elastic strain energy reaches a critical level, which means that the released energy is higher than the dissipated energy.A large volume of failed rocks are released and the magnitude is usually larger than that of a strainburst(Ortlepp and Stacey,1994).Fault-slip burst is due to the slip alongpre-existing faults or along newly generated shear ruptures.When the shear stress along a fault or a shear rupture exceeds the shear strength, the fault or shear rupture will slip.As a result, a large amount of seismic energy will be released suddenly, with high ground vibrations or ground motions,and may trigger other types of rockbursts.Rockburst events have been reported in all mining countries (e.g.South Africa, Canada, Australia, USA, China, India,Poland, and Chile) since the first such events were recorded in South Africa and India at the turn of the 20th century(Hedley,1987;Blake and Hedley,2003).Fig.2 shows a historical rockburst map of more than 1100 events from near 50 areas in the world during the period of 1995-2019.On March 9, 2005, a mining-related seismic event with a Richter magnitude of 5.3 occurred in the Klerksdorp District in South Africa, killing two miners and injuring 58 people(Durrheim,2010).On November 28,2009,a serious rockburst with a Richter magnitude of 2 occurred in a drainage tunnel in the Jinping II Hydropower Station in China, resulting in seven deaths and the destruction of a tunnel boring machine(TBM)(Zhang et al.,2012a).On May 31, 2015, a rockburst event at the Neelum-Jhelum Hydropower Project in Pakistan killed three workers and destroyed a TBM(Naji et al.,2018).The large quantity of rockburst events and the severity of those incidents are incontrovertible evidence that rockburst is a universal and serious problem that requires immediate attention.

Fig.1.Examples of rockbursts at a diamond mine in Canada.

At present,great efforts have been devoted to the investigation of rockbursts.Most research is focused on the mechanisms,contributing factors,risk evaluation and prediction,and prevention and mitigation of rockbursts.The methodologies of studying rockbursts can be generally summarized into five types:empirical,analytical, experimental, data-based, and numerical, as shown in Fig.3.Manouchehrian and Cai(2018)stated that there is not yet an effective way to control rockbursts because the phenomenon is so complex and is influenced by many factors (e.g.complexity and uncertainty in geological conditions, in situ stresses, induced stresses and triggering conditions (Gao et al., 2019a)).Empirical methods are generally site-specific and therefore difficult to generalize.Both analytical and experimental methods employ many idealized assumptions which are incapable of matching the real field circumstances.For instance, experimental testing conditions are usually designed to represent field conditions, but the rock behavior in experimental conditions may be very different from that in field conditions owing to the different properties of intact rocks and rock masses (Manouchehrian, 2016).Data-based methods are reasonable and accurate only if a sized and accessible database is provided (Zhou et al., 2018a; Pu et al., 2020).

Over the last five decades,with rapid developments in computer software and hardware,significant progress has been made in using numerical modeling to simulate physical phenomena in rock mechanics and rock engineering at various scales.Compared with other methods such as physical simulation and field tests, the numerical modeling method has the advantages of low cost,safety,timesaving,and flexibility.Also,it can provide more information.Salamon(1993)stated that different aspects of the rockburst problem(e.g.the relationship between mining activities and the related seismicity,source mechanism,and the effects of seismic waves on mining excavations)would benefit from numerical modeling.To date,numerical simulation methods have been widely used to evaluate the mechanical response of complex rock masses and to study rock mass deformation and failure mechanisms.Since the 1970s, these methods have also provided a common and even necessary way to study rockbursts.Therefore,it is necessary and meaningful to conduct a review of the current state of rockburst numerical modeling and to analyze the limitations and prospects in this research field.

In this study,the categories and the origin of different numerical approaches employed in modeling rockbursts are reviewed and the current usage of various numerical approaches is investigated by a literature research.Also, a state-of-the-art review is implemented to investigate the application of numerical modeling in the mechanism study,and prediction and prevention of rockbursts.The main achievements and problems are highlighted.Finally, this paper discusses the limitations and future research directions of this topic.An approach of numerical modeling for rockbursts is also proposed in order to provide researchers with a systematic and reasonable numerical modeling framework.

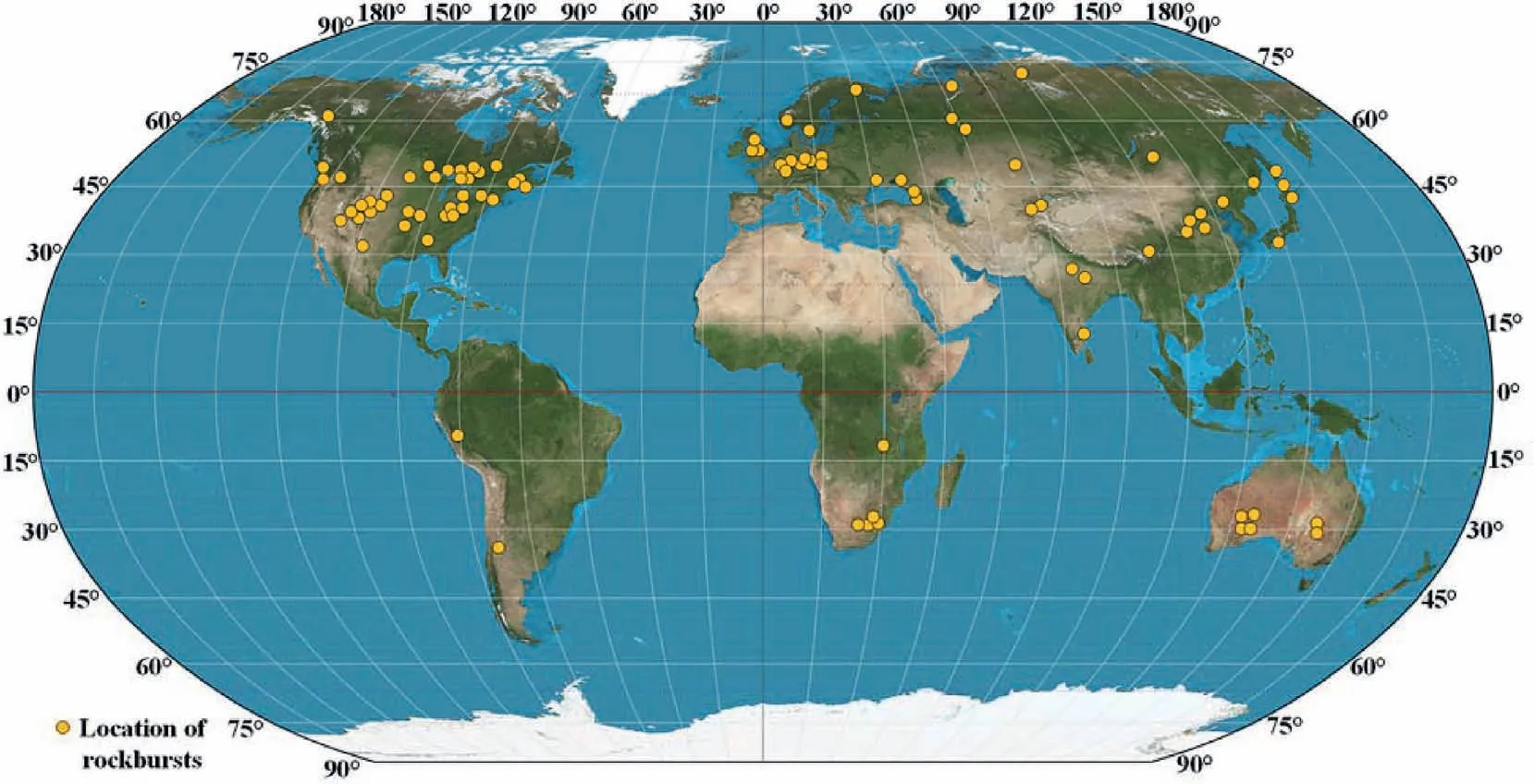
Fig.2.A historical rockburst map for the period of 1995-2019 (updated after Bennett and Marshall, 2001).

Fig.3.A summary of methodologies for studying rockbursts (after Manouchehrian,2016).

2.Numerical approaches for modeling rockbursts

2.1.Category of numerical approaches

With the rapid development of information technology(IT)and computer equipment, the availability of high-powered computer equipment such as supercomputers, cloud computing, and a large number of numerical approaches as well as a great variety of commercial or academic codes has opened avenues for the analysis and evaluation of complex problems in rock mechanics and rock engineering.Nevertheless, it is critical for researchers and engineers to discriminate amongst different numerical approaches and codes before using numerical modeling to tackle rock mechanics problems(Wagner,2019).According to Jing and Hudson(2002)and Jing (2003), numerical approaches in rock mechanics can be classified into continuum, discontinuum and hybrid methods(Table 1).The main subtypes and related commercial or research codes at present are also listed in Table 1.This review is particularly focused on numerical modeling for rockbursts.The detailed discussion of the concepts, principles, advances, and development of various numerical approaches used in rock mechanics and rock engineering has been excellently reviewed by Jager and Ryder(1999), Jing and Hudson (2002), Jing (2003), Brady and Brown(2004), Nikoli′c et al.(2016) among others.

2.2.Origin of numerical approaches employed in modeling rockbursts

Employing numerical approaches to investigate rock mechanics problems has been a common practice dating back to the 1960s(Salamon, 1964; Jing and Hudson, 2002; Jing, 2003), while numerical modeling to study rockburst-related problems was introduced a little later, in the 1970s.

The hazard of spalling is an important consideration when rock faces are subjected to dynamic loading induced by blasting or rockbursts near a permanent mine opening.Miranda (1972) first developed a finite difference computer code to simulate the elastic pulse propagation problem in the Split-Hopkinson pressure bar(SHPB)technique.He found that the computed numerical gage data agreed well with the derived strain and strain rate-time curves of the specimen.In the same year,Blake(1972a)acted as a pioneer in using the finite element method(FEM)model to study pillar bursts.He found that the areas of high stress concentration could be used as a sign to predict rockburst locations.Brady(1979)developed the boundary element method(BEM)with a proposed complete plane strain concept and first used it to study the unstable failure of pillars (pillar crush).He also put forward a cutting-edge idea:modeling surrounding rock as an elastic continuum by exploiting the efficient BEM and treating pillars as inclusions within which more complex constitutive equations were proposed, for example,the finite difference method (FDM) might be used in pillars to model the complex behavior of rock materials.Maybe this is the origin of the hybrid method concept.Board and Voegele (1981)employed a hybrid and a digital computer model utilizing the displacement discontinuity method (BEM) to study stress and displacement changes.Then they used the calculated energyrelease rate(ERR)to examine the effect of mining in an underhand fashion on the potential for sill pillar bursting.The results suggested that the ERR was lower when a larger sill pillar remained,but its magnitude was still enough to cause a pillar burst.This shows that numerical simulation is a useful and potential tool to evaluate rockburst risks and to improve mining design.Hart(1980)used the explicit FDM code,STEALTH,and the BEM code,MINAP,to evaluate rock failure and dynamic instabilities (rockbursts) based on the ERR.He concluded that for the elastic simulation,the results from the two codes were close and the BEM model was much easier to formulate and less expensive to run.However, the results also suggested that stored energy simulated by MINAP using the elastic constitutive model was smaller than that using STEALTH employing a nonlinear constitutive model, due to the lack of plastic deformation stage.This shows how important it is to select a reasonable constitutive model for geotechnical modeling.Zubelewicz and Mroz (1983) combined the FEM and a dynamic approach to study rockburst processes in a rock pillar, excavation faces, and tunnels.They also confirmed that the dynamic mode of failure can be numerically studied for any specified configuration and initial conditions.

Table 1Overview of numerical approaches and codes in rock mechanics.

The usage of the discontinuum method for modeling rockbursts is later than that of the continuum method, since more latter researchers began to notice the significance of discontinuities such as joints, which control and influence the mechanical behaviors of rocks,as well as the requirement of the large displacement of rocks,while the continuum method is based on the hypothesis of continuous small deformation.The discrete element method(DEM)is a discontinuum modeling approach that can,in a straightforward manner,model large displacements,disintegrations,rotations,and general nonlinear constitutive behaviors for both rock masses and joints.After the DEM was developed and established(Cundall,1971,1988; Cundall and Strack, 1979), Lemos et al.(1987), as the first researchers, used it to investigate the features of jointed rocks subjected to dynamic loading such as rockbursts.They stated that the DEM provided a useful tool for understanding a wide variety of dynamic problems in jointed rock masses.The discrete fracture network (DFN)is a special discrete method that is the most useful for the study of flow in fractured rock masses (Jing and Hudson,2002; Jing, 2003).Arndt et al.(2009) used the DFN model to conduct dynamic tests of a very heavy support system in order to investigate seismic hazards to ground support.Sun et al.(2007)investigated rockbursts in a circular tunnel under unloading conditions using realistic failure process analysis (RFPA) program and discontinuous deformation analysis(DDA).In order to simulate the gestation process of rockbursts,the failure patterns of surrounding rocks of a circular tunnel were first studied by RFPA, taking into consideration the non-homogeneity of rock materials and different in situ stresses.The crack lines and some potential cracks in the RFPA model were then imported into the DDA model to explicitly simulate the dynamic processes of a rockburst.The results suggested that the loss of stability of the surface rock mass was an omen or the beginning of a rockburst.However, Sun et al.(2007)also pointed out that the rock masses had to be discretized artificially in the DDA model and that the released strain energy was ignored in the DDA model.Hence, an improved simulation of rockbursts needs to be further investigated.

Jing (2003) reported that the main influence area of damage is concentrated near the excavation face and that linear material behavior is exhibited in the far-field region without fractures.Therefore, the discrete method is more suitable for near-field analysis, while the continuous method is more suitable for farfield analysis.Thus, it is a good way to combine those two numerical methods, which simultaneously makes full use of their respective advantages and avoids their disadvantages.Daehnke(1999) analyzed the dynamic fracturing due to the interaction of primary(P)and secondary(S)waves with stopes by implementing a parametric study through the FEM/DEM code ELFEN.The results verify that ELFEN can accurately simulate stress wave interactions and dynamic fracturing in underground excavations.After the FDM/DEM coupled method was proposed and developed (Itasca Consulting Group, Inc., 2000), Hazzard and Young (2002) adopted it to model microseismic(MS)activities surrounding a deep tunnel.The target area was modeled by an assemblage of particles from particle flow code (PFC) and was then coupled with the fast Lagrangian analysis of continua (FLAC) program.Although themodel is clearly a large simplification of realities, the simulation results, such as seismic locations, magnitudes, and mechanisms obtained from the numerical model compared with seismic data in the field,give further confidence that the FDM/DEM coupled model can behave in a realistic fashion.Later, Cai et al.(2007) employed the FLAC/PFC coupled numerical model to investigate excavationinduced acoustic emission (AE) activities in large-scale underground excavations.In the modeling, PFC was used to simulate AE sensors around surrounding rocks and the remaining rock masses were modeled by FLAC.The simulated AE activities were in good agreement with field monitoring results, which confirms that the coupled numerical method as an advanced tool can be applied to the interpretation of monitoring data and stability evaluation of large-scale underground excavations.SPECFEM2D is a powerful software package that can simulate the propagation of acoustic and elastic waves in a variety of media such as fluids, elastomers, viscoelastics,and anisotropic and porous objects,but it does not have the ability to analyze excavation-induced stress.By combining FLAC/SPECFEM2D, Wang and Cai (2017) proposed a coupled numerical method for a nonlinear velocity model to study the excavation effect on the ground motion in an excavation boundary.They found that the amplification effect at the excavation surface agreed well with underground field observations and when the simulated excavation rock was of fair quality,the excavation boundary of the stope had a stronger ground motion and wider seismic response.The coupled numerical method is helpful to better estimate ground motion parameters in dynamic load support design and can provide reasonable ground motion evaluation parameters in an inversion analysis of rockburst damage.Fig.4 shows the development process of various numerical methods employed in the history of modeling rockbursts.

2.3.Usage investigation of numerical modeling for rockbursts

In order to understand the usage of various numerical approaches to model rockbursts, we used “TS＝(rockburst* OR rock burst*)AND TS ＝ numerical”as query words in the Web of Science database to carry out an investigation about literature published during the last 20 years.It is very hard to search all published literature about this topic due to copyright and access-related issues.However, after reviewing the published literature one by one in this well-accepted and authoritative database and having relatively large amounts of data, we were confident that our investigation basically reflected the usage situations of various numerical approaches to model rockbursts.The search results are shown in Figs.5-7, and the variation laws are summarized as follows:

(1) Fig.5 shows that since 1999,the amount of literature in this field has increased.From 1999 to 2008, the growth was not very apparent, and the number of published articles increased only from three to seven.After 2009, the number of published articles grew rapidly although they may suffer decreases in a few years.After 2016, the number of publications was nearly 10 times that of 1999.Moreover, most researchers choose the continuum method for addressing rockburst-related problems.After 2014, more and more researchers begin to use the discontinuum and hybrid methods.

(2) As shown in Fig.6,the most common numerical approach is the continuum method (77.36%) and the second most common is the discontinuum method (19.54%).The hybrid method accounts for only 3.1%.For the continuum method,FEM and FDM are the most popular numerical methods(94.1% in total).Furthermore, in the FEM, the widely used numerical programs are ABAQUS (13.27%), ANSYS (11.22%),and RFPA2D (22.45%).Suit3D (14.29%) and Map3D (35.71%)are the most popular codes in the BEM,while FLAC(20.72%)and FLAC3D (76.89%) account for the largest proportion in the FDM.For the discontinuum method, DEM is the most popular(93.33%in total).The reason that there is no DFN in the pie chart is that DFN is the built-in function in some programs such as ABAQUS, FLAC3D, and 3DEC.Thus we did not show it in a single segment.In the DEM,the most popular codes are UDEC(54.46%),3DEC(9.86%),and PFC2D(17.86%),respectively.For the hybrid method,the DEM/FEM(47.37%)is widely used, in which FLFEN (55.56%) is the most common numerical program.

(3) In reality, rockburst types are various according to different researchers (Zhou et al., 2018a).Therefore, we classified thepublished literature as static and dynamic simulations,respectively,based on loading conditions and seismic waves.As shown in Fig.7a, from 1999 to 2008, most numerical modeling of rockbursts was conducted by static simulation and then there was rapid growth after 2009,especially after 2015.In 2016-2018, the proportion of dynamic simulation was more than 30%in each year.Overall,from Fig.7b we can see that most researchers employ static simulation to investigate rockbursts (71.34%).

Fig.4.History of numerical methods employed in modeling rockbursts.

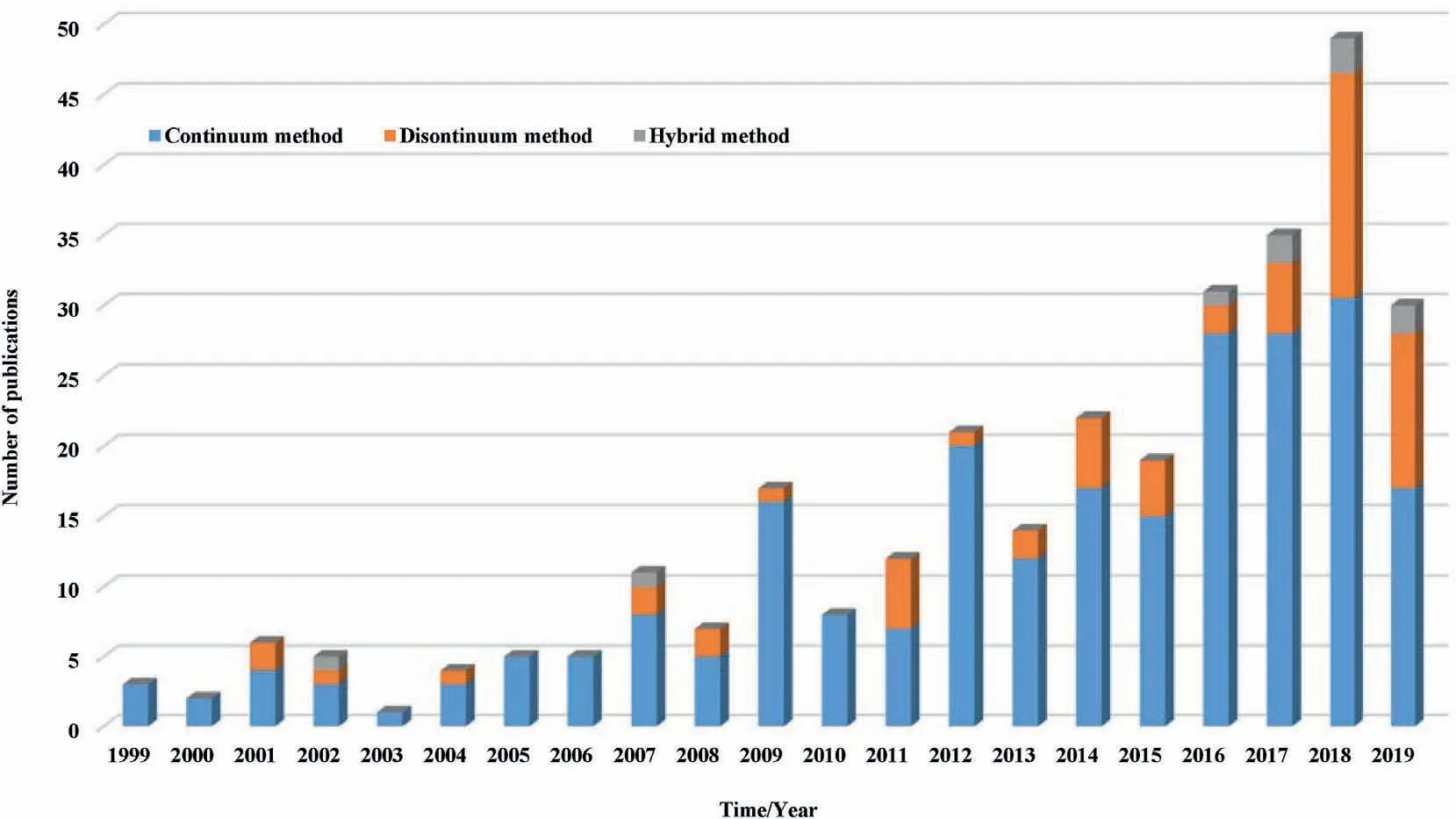
Fig.5.Literature about numerical modeling of rockbursts in the last 20 years (the search results in 2019 are incomplete).

3.A state-of-the-art review of the application of numerical modeling for rockbursts

3.1.Numerical modeling for rockburst mechanism

The initial studies of rockburst mechanisms through numerical modeling were based on some specific engineering cases,in which the continuum method, elastic constitutive relationship, and twodimensional (2D) model were very often used owing to the lower computation cost and modeling ability at that time,although many researchers noticed that using elastoplastic constitutive relationships and three-dimensional (3D) models was a better choice.In this stage, researchers tried to reveal the rockburst mechanism by modeling the changes of maximum principal stress, strain energy,and deformation after mining or excavating activities(Blake,1972a;Miranda,1972; Brady,1979; Board and Voegele,1981; Napier and Stephansen,1987; Bardet,1987,1990).

After that, with the development of computing capacities and progress in numerical programs for modeling complex geometry and plastic nonlinearities, more researchers tended to utilize elastoplastic constitutive relationships and/or 3D models(Blake,1972a;Miranda, 1972), and representative studies are listed in Table 2.Rockburst is a type of rock failure phenomena caused by the initiation,growth,and expansion of micro-fractures,which then form a macroscopic fracture(Wang et al.,2006).After confirming that AE parameters are related to the damage variable of rocks,Wang et al.(2003) used RFPA2D to simulate pillar bursts and found that the simulation results can reflect the macroscopic failure evolution process induced by microscopic fractures,and the spatio-temporal distribution characteristics of AE events.Using RFPA2D,Wang et al.(2003) also studied the effects of rock heterogeneity on rockburst potentials.Then,Wang et al.(2006)employed RFPA2D to study the progressive failure process and associated MS behavior of rock pillars.The simulated results verified that the stiffness of the roof and floor play an important role in controlling the unstable failure or collapse of rock pillars.Zhu et al.(2010)used RFPA-Dynamics to simulate the rockbursts triggered by the dynamic disturbance around a deep underground opening and confirmed that the dynamic disturbance is one of the most important contributing factors inducing rockbursts.

Most of the aforementioned work is limited to the study of rock failures based on the small deformation rule.In fact, the gestation and development of rockburst is a process from static failure to dynamic failure, which is transformed from a continuous small deformation into a discontinuous large deformation in a very short time.It is difficult to simulate the discontinuous deformation behavior of rock masses based on continuum methods such as FEM,BEM,and FDM.To this end, scholars tended to use DEM and other hybrid numerical methods suitable for simulating discontinuous deformation to reproduce rockburst phenomena.After years of development, the DEM has made great progress in both theories and applied research: (1) from rigid elements to deformable elements; (2) from 2D to 3D modeling; (3) from the simulation of static problems to the simulation of dynamic problems; and (4)from the single mechanical simulation to the simulation of multiphase media and multi-field coupling problems.The general block DEM considers the rock mass to be composed of discrete rock masses and joint faces between rock blocks.The rock mass can move, rotate, and deform, and the joint faces can be compressed,slid, and separated to more realistically simulate the continuous and discontinuous deformations of jointed rock masses (Jiang,2017).Therefore, the DEM and DEM-related hybrid methods are undoubtedly a good choice for the numerical modeling of the continuous-discontinuous deformation behavior of the rockburst gestation and failure processes.The corresponding studies are also summarized in Table 2.Recently, Vazaios (2018) and Vazaios et al.(2019) used FDEM (FEM/DEM) models through IRAZU to investigate the effect of pre-existing joints on strainburst phenomena in adeep hard rock excavation.To conduct a parametric study, three numerical model configurations were created.The first configuration did not include any structures (massive rock masses), and the two other configurations included stochastic joints by integrating a different number of DFNs.In those models, the initiation, propagation, and coalescence of fractures and abrupt rock ejection occurring in the excavation under high-magnitude stresses were able to be explicitly simulated(part of results are shown in Fig.8).Fig.8 shows that rock blocks located around the excavation boundary possess higher velocities than those far away from the excavation wall,which is the reality(Ortlepp and Stacey,1994;Qiu et al., 2014).Additionally, larger ejected volumes are generated with the increasing number of pre-existing joints which also govern the shape and size of ejected rock blocks.The FDEM models have made it possible to simulate the change from a continuous deformation to a discontinuous deformation to reproduce the physical process of rockburst phenomena, which further highlighted the application of the hybrid method in rockburst numerical modeling.

Fig.6.Distribution of different numerical methods in modeling rockbursts in the last 20 years (the search results in 2019 are incomplete).

In summary, the employment of various numerical methods,codes, and constitutive models at different dimensions and scales has greatly enriched people’s understanding of the complex source mechanism and damage mechanism of rockbursts.Compared with continuum methods, the DEMs, especially DEM-related hybrid methods, have achieved the explicit simulation of rockburst process,providing an effective tool for researchers to reveal the nature of rockbursts.This might motivate more researchers to use discontinuum and hybrid methods in this research field.However,it is not true because these methods are not flawless.To eliminate the effects of mesh size on the fracture position within rocks,a very finemesh resolution is usually needed, which sacrifices the computational efficiency of the model.Moreover, the calculation time will be greatly extended when the blocks or elements undergo a large deformation and are detached from each other (Gao, 2019).For instance,Vazaios et al.(2019)reported that the total run time of the third model configuration is around 100-144 h.This is an important reason why discontinuum and hybrid methods are less used than continuum methods (see Fig.6).It should be noted that we cannot easily say which numerical method is better to simulate rockburst mechanisms since every method has its own advantages and limitations (Table 3).The selection of numerical methods should be based on the match between the capabilities of numerical codes and rockburst mechanisms,and the specific engineering situation.To provide some references for researchers and engineers, a simple guideline for choosing numerical methods is summarized based on this review and authors’ experience over the years (Fig.9).

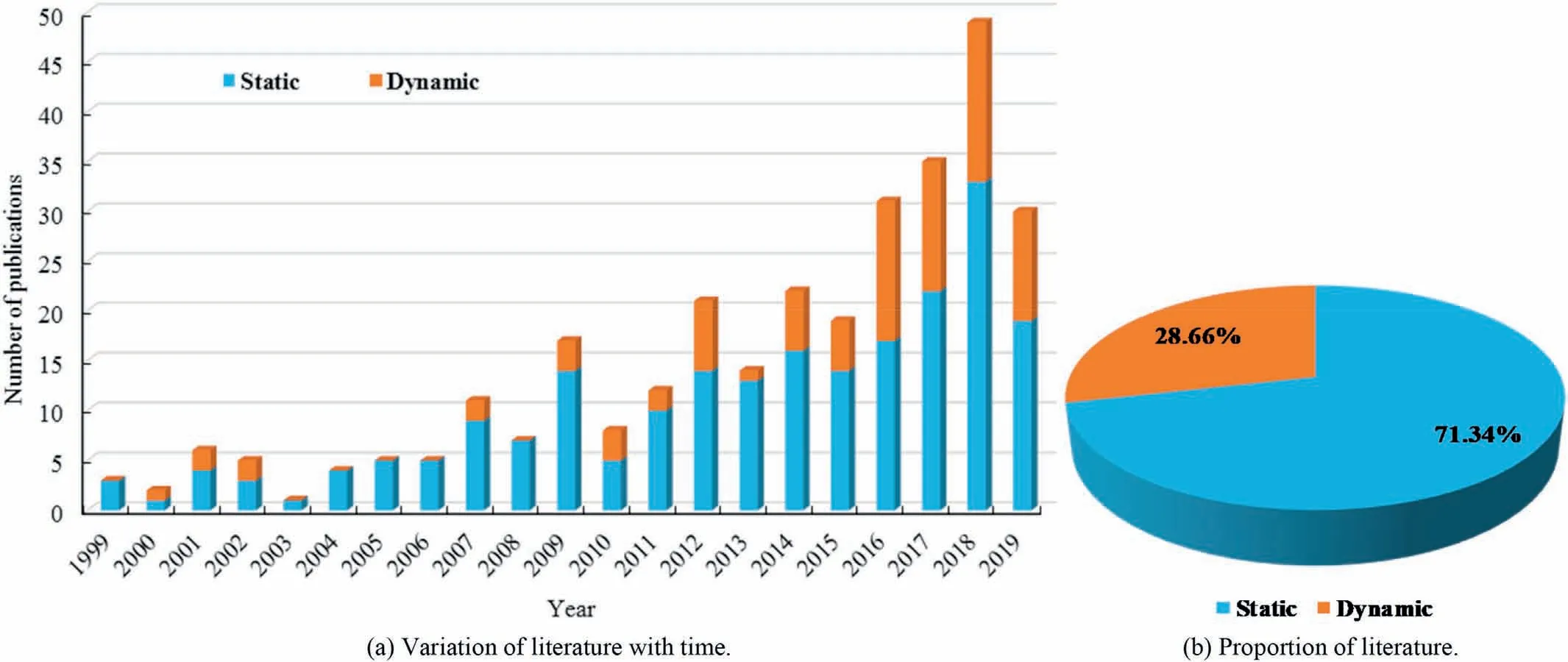
Fig.7.Literature about static and dynamic simulations of rockbursts in the last 20 years (the search results in 2019 are incomplete).

3.2.Numerical modeling for the evaluation and prediction of rockbursts

Researchers agree that it is very difficult to accurately predict the occurrence time of rockbursts due to the randomness and complexity of the mechanism of rockbursts(Qian,2014;Zhou et al.,2018a).However, the occurrence of rockbursts is mainly determined by the change in ground stress caused by the excavation of deep rock masses.The geological survey technology,ground stress detection technology, rock mechanics theories and methods, and long-term development of numerical simulation have made it possible to perform qualitative and quantitative prediction of the location and intensity of rockbursts (Qian, 2014).Scholars believe that the era of quantitative prediction of rockbursts has arrived,and such quantitative progress needs to be achieved through a combination of numerical simulation and on-site observation (Stacey,2013; Cai, 2016).

In the past few decades, scholars have proposed a number of prediction and evaluation indices or indicators of rockburst potential based on a variety of rockburst theories, and rockburst phenomena from the aspects of strength,stiffness,energy,stability,fracture, damage, etc (Li et al., 2013).To learn about the complete and detailed prediction and evaluation indices or indicators of rockbursts,readers are recommended to references(Zhang and Fu,2008; He et al., 2012; Li et al., 2013; Qian, 2014; Mazaira and Konicek, 2015; Feng et al., 2017b; Leveille et al., 2017; Zhou et al.,2018a; Afraei et al., 2019; Jiang et al., 2019; Pu et al., 2019).At present, the proposed prediction and evaluation indicators of rockbursts can be generally classified into two categories: (1) indicators based on the stress/strength criterion, such as tangential stress,axial stress,uniaxial compressive strength(UCS),and major principal stress, in which the representative indices are σθ/σc(Russenes,1974),σc/σ1(Barton et al.,1974),σL/σc(Turchaninov et al.,1972),σc/σθ(Hoek and Brown,1980),σc/σ1(Tao,1988),excess shear stress(ESS)(Ryder,1988),σc/σt(Peng et al.,1996)(σ1-σ3)/σc(Castro et al., 2012), etc.; and (2) indicators based on the energy criterion,such as elastic strain energy and elastoplastic deformation energy,in which the representative indices are strain energy storage coefficient(Wsp/Wst)(Kidybi′nski,1981),the ratio of kinetic energy to released energy (Wk/Wr) (Hedley, 1992), ERR (Salamon, 1984;Kaiser et al.,1996), burst potential index (BPI) (Mitri et al.,1999),local energy release rate (LERR) (Wiles, 2002; Jiang et al., 2010),loading system stiffness (LSS) (Wiles, 2002), strain energy density(SED) (Wattimena et al., 2012), etc.Due to the complexity of the geological and construction conditions,and mining-or excavationinduced effects, it is very difficult to predict and estimate rockbursts based on analytical and experimental methods, because many idealized assumptions are employed in these methods.By contrast, numerical modeling can simulate the elastoplastic,nonlinear,and post-yield behavior of rock masses and the effects of in situ stresses and geological features on mining or excavating works,which enables researchers to understand the“real world”in underground engineering.Thus, using numerical modeling with the prediction and evaluation indices is a useful tool for researchers and engineers to estimate rockbursts.

The studies about numerical modeling and prediction of rockbursts are summarized in Table 4.As shown in Table 4, different indicators (stress/strength-based, or energy-based) have been widely employed to assess and predict rockburst potentials in various engineering projects.In addition to basic variables such asstress and strength, some more complex rockburst indicators,either empirical or user-defined, can be easily obtained by processing the basic variables using the built-in or common programing languages (e.g.Fish language in FLAC3D, C＋＋, Python,etc.) in most numerical programs.The use of these indicators combined with numerical methods has become an easy,useful,and applicable approach to predict rockburst risks qualitatively and quantitatively for research and engineering projects.However, it should be noted that different prediction and evaluation indicators of rockbursts have their best application conditions and scopes.Because most of these indicators are based on some specific cases from different regions in the world, of which the geological conditions, rock properties, geometry of engineering, and excavatinginduced effects are very different.For instance, Mitri et al.(1999)pointed out that ERR values in a Canada mine are much lower than those leading to rockburst problems in South African mines.The rockburst indicators cannot be directly transposed to the particular situation from one to another region.Furthermore,although many researchers reported that the effectiveness of rockburst indices had been verified with on-site monitoring results,these indices cannot be popularized casually even in the same region due to the small number of rockburst cases and the randomness and complexity of rockburst mechanism.Therefore, a strict calibration procedure should be implemented before using indicators to predict and estimate rockburst tendency.A methodology is proposed to effectively evaluate rockburst potentials using numerical modeling combined with laboratory tests and feedbacks from the field.A flowchart of the proposed methodology is shown in Fig.12.The first step is to evaluate the rockburst proneness of rocks based on indicators at a laboratory scale.If the rock does not possess rockburst proneness,rockbursts will not occur during rock mass engineering in this kind of rock(Cai,2016;Leveille et al.,2017;Zhou et al., 2018a).The second step is to choose indicators (engineering scale) initially and to predict rockburst tendency using numerical simulation.The selection of rockburst indicators can refer to a summary made by Zhou et al.(2018a): FAI (failure approaching index,Zhang et al.,2011),BSR(brittle shear ratio,same as(σ1-σ3)/σc,Castro et al.,2012),ERR(Salamon,1984;Kaiser et al.,1996), BPI (Mitri et al.,1999), and LERR (Wiles, 2002; Jiang et al.,2010) can be used for evaluating strainbursts; and ESS (Ryder,1988), BPR (bursting potential ratio, Simon, 1999) and OBI (outof-balance index, Simon,1999) are suitable for assessing fault-slip bursts.However, Zhou et al.(2018a) did not mention what indicators could be adopted to estimate pillar burst risks.Some researchers (Wiles, 2002; Castro et al., 2012; Kusui et al., 2016;Vennes and Mitri, 2017; Li et al., 2019) suggested that the ERR(Salamon,1984; Kaiser et al.,1996), LSS (Wiles, 2002),σc/σθ(Hoek and Brown, 1980), BSR (Castro et al., 2012), and SED (Wattimena et al., 2012) could be employed for the assessment of pillar burst potentials.Then the selected indicators can be calculated in numerical programs, thereby letting us either determine or update the indicators initially by comparing the occurrence area and intensity of a rockburst case in the field.In the third step, the reasonable indicators are finally obtained after the calibration with more rockburst cases or a rockburst database of this region.Following these three steps, engineers will be confident to use some indicators as rockburst criteria to predict risks quantitatively and to take appropriate measures for rockburst prevention.

Table 2Summary of theapplications of numerical modeling for rockburst mechanisms.

Fig.8.Effects of different pre-existing joints on strainburst phenomena (from Vazaios et al., 2019).

Table 3Advantages and limitations of numerical methods in modeling rockburst mechanisms.

3.3.Numerical modeling for the prevention and mitigation of rockbursts

After the burst-prone zones are predicted and evaluated, prevention and mitigation measures should be carried out.Generally,there are three approaches or steps for the prevention and mitigation of rockbursts, as shown in Fig.13.Estimating the effects of those measures in fields is very dangerous, time-consuming, and costly.For instance,distress drilling is a very common technique to mitigate rockburst risks in the field.The design parameters of boreholes such as diameter,length,position,and pattern layout are normally determined according to engineers’ specialization and experience.However, the design parameters depend on many factors, e.g.the size and shape of excavations, mechanical properties of rocks, and in situ stress.Thus, engineers need to spend tremendous time and money costs to obtain relatively ideal design parameters considering many influencing factors of distress drilling.Besides,conducting experimental schemes of engineers in the field will always make personnel be exposed in a dangerous environment.In contrast,numerical modeling is a cheap,fast,safe,and effective tool for the evaluation of those three types of measures,especially when optimizing support design and project layout(Mazaira and Konicek, 2015).

The studies about numerical modeling of rockburst prevention are summarized in Table 5.As shown in Table 5, numerical modeling has been widely employed to assess the effects of various techniques on the prevention and mitigation of rockburst risks.For the first type of rockburst prevention approach, the 3D modeling with elastic analysis is a fast and effective method to determine the areas with stress concentration and energy accumulation in the design stage, thereby letting engineers choose rational project layouts, and mining/excavation methods to avoid potential rockbursts.In the production stage, some calibrated rockburst indicators can be used to estimate the rockburst tendency so as to adjust construction schemes or adopt distress and support measures in time.In contrast, the situation of modeling ground preconditioning and rock support is very complex.At present, the main approaches to simulate the effects of destress blasting are reducing the rock properties such as elastic modulus or adding a stress dissipation factor to model the instantaneous stress drop(Blake, 1972b; Tang and Mitri, 2001; Sainoki et al., 2017; Vennes and Mitri, 2017).Although these methods are very simple to use,no actual blastholes exist in the numerical model,which is indeed atype of equivalent approach.Moreover, specific zones with potential blasting-induced damages need to be assumed first to assign parameters, which is not real and increases extra efforts.By analyzing a pressure profile of ANFO-type explosive and the propagation of detonation, Sainoki et al.(2017) proposed an innovative method that can simulate a time-varying blast pressure.Using this method,the blasting-induced damage can be simulated more precisely.Nevertheless,the volume dilation of rocks induced by the creation and development of fractures was neglected,because the continuum method was used in the previous work.A Trigon method developed by Gao (2013) can simulate the obvious dilation phenomenon caused by the generation and propagation of cracks, which can be further adopted to evaluate the blastinginduced damage and the dissipated energy induced by rock fracturing.The numerical modeling of water infusion is less studied owing to the infrequent usage of water infusion for hard rock engineering.Currently, numerical simulation is mainly utilized to examine the effects of water infusion on mitigating coal burst risks(Li et al., 2005; Fan et al., 2012; Song et al., 2014; Liu et al., 2017;Zhou et al.,2018b).Numerical modeling of rock support systems is probably one of the most important and extended applications of numerical methods to underground excavations, and its importance is even greater when designing support systems in burstprone grounds (Mazaira and Konicek, 2015).Numerical analyses in this field mainly focus on the behavior of support elements such as rockbolts and steel arches under dynamic loading, or stress waves produced during rockbursts.The main problem is that researchers need to develop reasonable models to reproduce the realistic response of support elements, requiring many efforts to calibrate the models with experimental data or in situ observations.Besides, engineering experience shows that the failure of reinforcement elements often occurs in the rockbolt-grout interface rather than the grout-rock interface (Marambio et al., 2018).However, the input parameters for modeling rockbolt-grout interfaces are usually set based on researchers’ experience, which need to be further investigated to capture the full mechanical behavior of rockbolt supporting.

Fig.9.Selection of numerical methods for modeling rockburst mechanisms.

Table 4Summary of the applications of numerical modeling for rockburst prediction.

Table 4 (continued)

Fig.10.Redistribution of the strength factor (a) before and (b) after floor benching (after Apel, 2005).

4.Limitations and future research

4.1.Dynamic modeling of rockbursts

As mentioned above, rockburst is a kind of dynamic disasters that develop from the static accumulation of mining-induced stress and strain energy.However, only a small portion of research(28.66%, as shown in Fig.7b) used dynamic modeling to study rockburst-related problems.Additionally, most existing indices or indicators of rockbursts that can be used for numerical calculations are proposed based on static simulation results, which can only make static and qualitative evaluations of rockburst risks, and cannot reasonably reflect the dynamic process of actual rockbursts(Yang et al.,2015).Therefore,the dynamic modeling of rockbursts is necessary.Some research work has already been implemented to investigate the effects of dynamic load or stress wave on rockbursts.But some questions remain:

(1) Dynamic mechanical properties of rocks and discontinuities.The reality and accuracy of numerical modeling resultsdepend on the mechanical properties of rocks and discontinuities.Only if the mechanical properties of rocks and discontinuities are scientific and reasonable can the numerical modeling results accurately reflect the actual deformation and damage of rocks or rock masses on site.It is well known that the mechanical properties of rocks and discontinuities are related to loading conditions and loading rates (strain rates).Up to now, a large amount of research has been conducted to investigate the dynamic mechanical parameters of rocks in the laboratory(Li et al.,1993,1994;Demirdag et al.,2010;Liu et al.,2012;Wang et al.,2016).Unfortunately,most present research that uses dynamic modeling adopts the static mechanical properties of rocks to study rockbursts.On the other hand, although a great deal of research has been done on the mechanical properties of rocks under dynamic loading in the laboratory, the study of dynamic mechanical properties of discontinuities is rare, and thus the dynamic mechanical properties of discontinuities are even less frequently used for the numerical simulation of rockbursts.For instance, Gao et al.(2019a, b) stated that the joint constitutive model in UDEC was obtained under the conditions of static loading.Whether this model can be used to simulate the dynamic response of jointed rock masses is worthy of further study.Therefore, the employment of the dynamic mechanical parameters of rocks and discontinuities as well as their constitutive relationships considering the loading rate (strain rate) in numerical modeling could be a research topic for rockburst-related problems in the future.

Fig.11.Estimation of rockburst tendency with σθ/σc (Ts) and BPI in a kimberlite pipe (after Sepehri, 2016).

(2) The heterogeneity of rocks and rock masses under dynamic loading.Manouchehrian and Cai(2018)pointed out that using homogenous material models may not be able to capture the realistic failure processes and patterns even if the overall stress-strain curve properly reflects the prescribed mechanical properties.To date, the material heterogeneity has been introduced into some numerical models to investigate the influence of rock heterogeneity on dynamic rock failure and associated energy release.However, the widely used numerical models are only 2D in laboratory scale,and the simulation results are not accurate and reliable.Hence,the simulation of the effects of rock heterogeneity under dynamic loading on rockbursts with 3D models at an engineering scale needs to be further studied.In addition, the distribution of rock heterogeneity is usually modeled with a normal distribution or Weibull distribution, while the real distribution of the heterogeneity of rocks is generally stochastic.Fortunately,recently developed 3D scanning and 3D printing technology can capture the stochastic distribution of rock heterogeneity,which will be a good choice for addressing this problem when combined with numerical modeling.

(3) Self-initiated dynamic disturbance.Researchers usually employ an assumed dynamic disturbance such as a sine P-waveform on the model boundary or inside the model to trigger unstable failures, which does not represent realsituations.Gao et al.(2019a, b) proposed a novel method:simulating a seismic event induced by dynamic rock fracturing through a strength reduction approach to initiate a dynamic disturbance in a rock pillar, which can produce P-and S-waves with related seismic wave properties such as velocity,the ratio of Vs/Vp,and frequency that are needed for evaluating strainbursts.Compared with most existing methods, this proposed method overcomes the difficulty of determining seismic wave properties of the dynamic disturbance input,which makes a significant step forward in the simulation of rockburst processes.Nonetheless, the location of the dynamic disturbance in the rock pillar is also manually determined, while in the field, the rock fracturing occurs randomly in many positions surrounding excavations and then produces a series of seismic waves or dynamic disturbances that may trigger rockbursts.Thus,one needs to address the problem that makes the rock fracturing induce seismic waves or dynamic disturbances spontaneously instead of assuming the positions of dynamic disturbances artificially.To handle this problem,theoretical and laboratory research is necessary to investigate the relationship between the properties of dynamic disturbances and rock fracturing.But the numerical fulfillment of that relationship in numerical modeling is quite sophisticated and a large amount of programming work needs to be done.

Fig.12.A methodology to evaluate rockburst potentials.

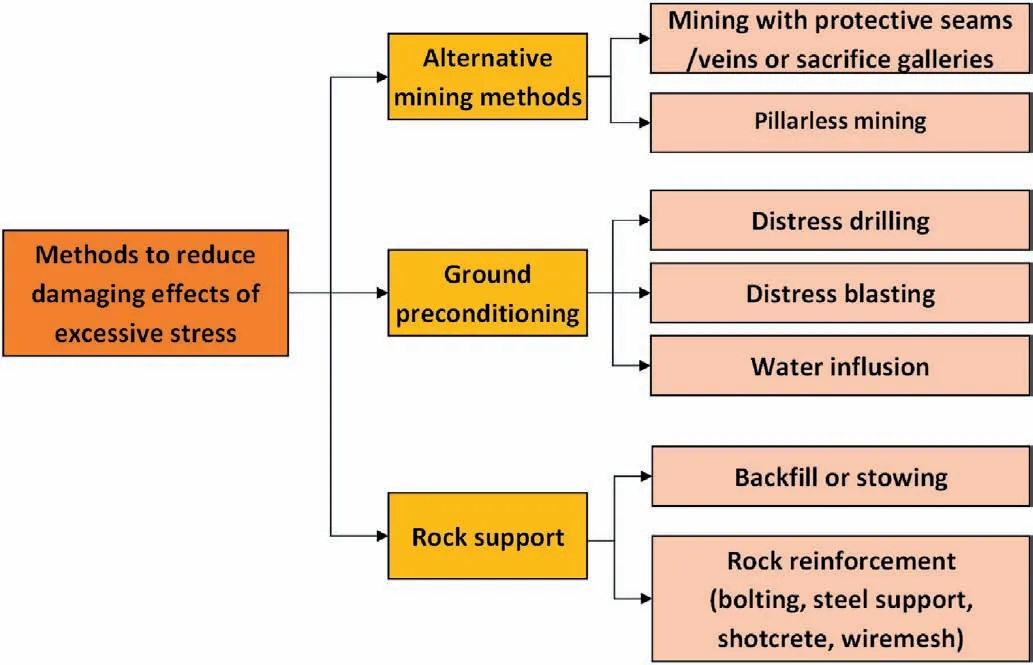
Fig.13.Methods to reduce damaging effects of excessive stress in underground mining(after Mitri, 2000).

4.2.Modeling of yielding support elements

Up to now,yielding supports or energy-absorption supports have been well developed owing to the tireless efforts of scholars.Verifications have shown that many types of yielding rockbolts,e.g.cone bolt (Ortlepp, 1992), Swellex rockbolt (Wijk and Skogberg, 1982),Roofex (Charette and Plouffe, 2007), D-bolt, Garford bolt (Varden et al., 2008), Yield-Lok (Wu et al., 2011), and constant-resistance and large-deformation bolt (CRLDB) (He et al., 2012) can control rockbursts effectively.Unfortunately, the development of yielding supportelements or yielding support models in numerical programs is lagging significantly behind the development process of those yielding supports in engineering practice.For instance, the conventional support elements (e.g.rockbolts) in some numerical programs are not able to handle high loads and withstand large deformations to control rockbursts.Thus,it is imperative to develop appropriate support elements or support models in numerical programs that can accurately simulate yielding support systems to estimate their performance during rockbursts.In addition, the properties of contact between rockbolts and grout, and the interaction or coupling effects between different support fashions (e.g.rockbolts and shotcrete)under dynamic loading are also expected to be further investigated to assess the full behavior of integrated yielding support systems in burst-prone areas.

4.3.Modeling existing discontinuities and new fractures in 3D models

Stead et al.(2004)and Coggan and Stead(2005)pointed out that the continuum and discontinuum methods are limited by their inability to capture the interaction between existing discontinuities and new fractures created in intact rocks.Fortunately, recently developed hybrid methods(e.g.DEM/FEM,DEM/FDM)provide the solution for this problem and some studies are currently underway(Feng et al.,2017a;Vazaios,2018;Vazaios et al.,2019).However,the current hybrid numerical models are usually 2D.It is reasonable that simulating a long tunnel based on the assumption of the plane strain condition,but it is invalid if the research objective is a rock pillar or a stope or more complicated excavations when the 2D model is applied.More importantly,the discontinuity consists of two rough surfaces,or two rough surfaces sandwiched with soft rocks or clays.It has both width and length, and thus it is neither accurate nor realistic to model it only as a line in a 2D model.Elmo et al.(2005)proposed that the out-of-plane continuity would lead to an easier creation of blocks,and in a 3D pillar model there would be greater freedom for failures to occur due to the lack of confinement coming outof the 2D plane,which means that the 2D model tendsto result in an overestimation of pillar strengths.Thus, the 3D modeling willprovide useful insight into the effects of existing discontinuities and newfractures on rockbursts.Further work needs to be undertaken to establish 3D models that incorporate existing discontinuities and new fractures created in intact rocks.

Table 5Summary of the applications of numerical modeling for rockburst prevention.

Table 5 (continued)

4.4.A systematic numerical modeling approach for rockbursts

Owing to the complicated mechanisms and the uncertainty of occurrence, rockburst is different from other rock mechanics problems such as stable failure modes (e.g.rock spalling) after tunnel excavation and ore extraction.Many contributing factors for simulating rockbursts should be considered when modeling this complex phenomenon.Thus,it is necessary to propose an approach of numerical modeling for rockbursts in order to provide researchers with a systematic and reasonable numerical modeling framework.The selection of numerical modeling approaches, numerical programs,numerical modeling sequences,parameters,and model calibration should be described in this method.The first step is the preparation which includes problem analysis, selection of numerical methods, and geometry analysis of the research objective.The second step includes five procedures: model establishment and meshing, input of in situ stress,constitutive models and rock mass parameters, initial and boundary conditions, geostatic step and model calibration, and analysis of simulation results.The details of this approach are shown in Fig.15.

5.Conclusions

This paper summarizes the categories and the origin of different numerical approaches for modeling rockbursts and the current usage of various numerical approaches is investigated.A state-ofthe-art review of the application of numerical modeling for studying rockbursts is implemented.This paper also discusses the limitations and prospects of rockburst numerical modeling.Anapproach of numerical modeling for rockbursts is proposed so as to provide researchers with a systematic and reasonable numerical modeling framework.The following conclusions are drawn from this study:

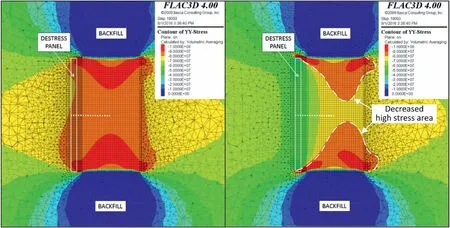
Fig.14.Stress state in the pillar before and after distressing (after Vennes and Mitri, 2017).Stress in Pa.

Fig.15.Flowchart of a systematic numerical modeling approach for rockbursts.

(1) Rockburst-related problems have been investigated by researchers using continuum, discontinuum and hybrid numerical methods and various numerical programs since the 1970s.The main tendency of rockburst numerical modeling is to move from continuum methods to discontinuum methods and then to hybrid methods.However, the most common numerical approach is still the continuum method.It is another tendency that using dynamic simulation to investigate rockbursts in this field.

(2) The initial studies of rockburst mechanisms through numerical modeling were based on some specific engineering cases, in which the continuum method, elastic constitutive relationship and 2D model were very often used.With the development of computing capacities and progress in numerical programs for modeling complicated geometry and plastic nonlinearities,more researchers utilized elastoplastic constitutive relationships and/or 3D models.Recently, the development of DEM and other hybrid numerical methods have made it possible to simulate discontinuous deformation to reproduce rockburst phenomena.The selection of numerical methods should be based on the match between the capabilities of numerical codes and rockburst mechanisms,and the specific engineering situation.

(3) Rockburst potentials can be predicted qualitatively and quantitatively using numerical modeling and a number of prediction and evaluation indices or indicators based on strength and energy criteria.These indicators have their best application conditions and scopes and cannot be popularized casually.A strict calibration procedure should be implemented before using indicators to predict and estimate rockburst tendency.

(4) Numerical modeling is a cheap and effective tool to evaluate the measures used for the prevention and mitigation of rockbursts.The dilation phenomenon of rocks should be considered to assess the blasting-induced damage and the dissipated energy induced by rock fracturing when modeling the distress blasting.The input parameters of rockbolt-grout interfaces need to be further investigated to capture the full mechanical behavior of rockbolt supporting.

To date, great achievements have been made by numerous researchers in employing numerical modeling to investigate the mechanism, evaluation and prediction, and prevention and mitigation of rockbursts.Nevertheless, rockburst is a very complicated geological hazard and the research of rockbursts through numerical modeling is always ongoing:

(1) One possible research topic for rockburst-related problems is to use the dynamic mechanical parameters of rocks and discontinuities as well as their constitutive relationships to consider the loading rate(strain rate)in numerical modeling.Using recently developed 3D scanning and 3D printing technology would be a good way to capture the stochastic distribution of rock heterogeneity.Theoretical and laboratory research is necessary to investigate the relationship between the properties of dynamic disturbances and rock fracturing.A large amount of programming work needs to be done to fulfill that relationship in numerical modeling.

(2) It is imperative to develop appropriate support elements or support models in numerical programs that can accurately simulate yielding support systems to estimate their performance during rockbursts.In addition, the properties of contact between rockbolts and grout, and the interaction or coupling effects between different support fashions under dynamic loading,are also expected to be further investigated to assess the full behavior of integrated yielding support systems in burst-prone areas.

(3) Further work also needs to be undertaken through the recently developed hybrid methods to establish 3D models that incorporate existing discontinuities and new fractures created in intact rocks.

Declaration of competing interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication, and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgments

The authors gratefully acknowledge financial support from the China Scholarship Council (Grant No.201808370185).

List of symbols

σcUniaxial compressive strength of rock

σθ Maximum tangential stress of surrounding rock

σ1Maximum principal stress

σtUniaxial tensile strength of rock

σLAxial stress of tunnel

σzVertical stress

γ Unit weight

ν Poisson’s ratio

α Tao discriminant index

D Diameter

EhAverage deformation modulus of the upper part of the Earth’s crust measured in a horizontal direction

EsUnloading tangential modulus of rock

k Ratio of the horizontal stress to the vertical stress

L Length

Tsσθ/σc

VsVelocity of secondary wave

VpVelocity of primary wave

WkKinetic energy

WrReleased energy

WspStored elastic energy

WstDissipated elastic energy

Z Depth

B Brittleness coefficient