Integration of three-dimensional continuum model and two-dimensional bonded block model for studying the damage process in a granite pillar at the Creighton Mine, Sudbury, Canada

Sankhaneel Sinha, Gabriel Walton

Geology and Geological Engineering, Colorado School of Mines, Golden, CO, 80401, USA

Keywords:Bonded block model (BBM)Rock pillars Supports Continuum-discontinuum integration

ABSTRACT Bonded block model(BBM)has shownpotential in replicating rock mass behavioras well as the rock-support interaction mechanism,but their practical application is limited totwo dimensions due to the high associated computational demand.To allow for the use of BBM in simulating three-dimensional (3D) problems, this study proposes an integrated 3D continuum-two-dimensional(2D)discontinuum approach,in context of rock pillars.A cross-section of a granite pillar was simulated using a BBM with a load path from a calibrated mine-scale FLAC3D model.Pillar support as employed in the mine was also incorporated in different stages during the simulation.The model was calibrated by varying the input parameters until the displacements at sixlocations withinthe pillarmatchedthose measuredbya multi-point boreholeextensometer(MPBX)inthe field.The calibrated model was subsequently used to understand how the support and load path influenced the damage evolution in the pillar.The shear component of the load path was found to have a major effect on the severity and extent of the damaged regions.When the support density was increased in the model,the lateral displacements along the pillar walls were significantly suppressed in a somewhat unpredictable manner.This was explained by the interaction between the supports and the damaged regions at the corners,which ultimately modified the stresses along the pillar periphery.The amount of displacement reduction obtained by increasing the support density illustrates the potential of BBM to be used as a support design tool.

1.Introduction

Pillar is one of the most important load bearing members in underground mines and plays a crucial role in sustaining the functional integrity of openings.With mining progressing to deeper depths, it becomes even more important to evaluate the integrity of such pillars,both from a localized skin-damage as well as a global failure standpoint.Although a complete collapse of a pillar is catastrophic and often violent in nature, it rarely occurs;extensile fracturing and geometric bulking of the rock mass along the pillar periphery, on the other hand, are more common, and support should be designed accordingly to manage instabilities and potential falls of ground resulting from large displacements.The extent and magnitude of stress-induced damage is controlled by a multitude of interacting factors, including but not limited to rock strength, stress path, support timing, and density (Kaiser et al.,1996; Diederichs, 2003, 2007; Diederichs et al., 2004; Cai and Kaiser, 2014).

Advanced numerical modeling techniques now allow us to investigate complex rock mechanics problems, which are otherwise difficult to study using low(spatial)resolution in situ data(e.g.data obtained by anchored extensometers and borehole pressure cells).Generally, numerical modeling techniques can be subdivided into two categories: continuum and discontinuum (Jing and Hudson, 2002).The most significant difference between the two categories is that discontinuum models allow for the formation and opening of explicit fractures while continuum models simulate this damage process using inelastic constitutive relationships.While continuum models may be more appropriate for large-scale(e.g.mine-scale)applications based on their relative simplicity and shorter runtime,if small-scale fracturing and damage are of interest(e.g.spalling), discontinuum approach may be more appropriate(Jing, 2003), which will be discussed in details below.

Excavations in massive to sparsely fractured rock mass at depth experience spalling, and such a behavior can be effectively simulated by continuum models using the cohesion-weakeningfrictional-strengthening (CWFS) model (Hajiabdolmajid et al.,2002).In essence, this model considers the non-simultaneous mobilization of cohesive and frictional strengths in rocks undergoing brittle fracturing (Martin and Chandler, 1994).While continuum models are undoubtedly capable of replicating the brittle rock damage process and the behavior of reinforced ground(Edelbro, 2009; Walton et al., 2014, 2016; Renani et al., 2016), a recent study by the authors (Sinha and Walton, 2019a) has shown that such models tend to significantly underestimate ground movements when supports are removed from the system.This is due to the inability of continuum models to accurately replicate large-scale deformation mechanisms, including separation and rotation of discrete blocks of rock.In the same study, Sinha and Walton (2019a) demonstrated how a polygonal bonded block model (BBM) could better capture the behavioral difference between unsupported and supported ground conditions, and accordingly suggested the use of discontinuum models for design of pillar skin supports.With this in mind and given the computationally demanding nature of three-dimensional (3D) discontinuum models, it is useful to establish an approach where a portion of a 3D mine-scale problem(e.g.asymmetrical damage in a pillar due to sequential stope extraction) can be analyzed using a two-dimensional (2D) discontinuum model.Ultimately, it should be possible to optimize the support layout at a site by varying the support density until target(or safe) displacements are attained.

This study is an attempt to establish such an integrated approach; in particular, we chose to simulate a cross-section of a supported granite pillar in the Creighton Mine (Sudbury, Canada)using the polygonal 2D-BBM approach.Other discontinuum approaches and software packages are available and could be applied for the same purpose (e.g.PFC2D: Wanne et al., 2004; Cai et al.,2007; Kias and Ozbay, 2013; PFC3D: Cundall et al., 2008; Ivars et al., 2011; Zhang et al., 2015; Zhang and Zhou, 2016; finite discrete element method (FDEM): Elmo and Stead, 2010; Li et al.,2019; Vazaios et al., 2019), but the focus of this study is on the BBM approach.A 2D approximation is valid in this case since the pillar is long (length (L) × width (W) × height (H) is 28.125 m × 7.5 m × 5 m; L/W is therefore 3.75) and previous research has found that the effect of increased length on pillar behavior is negligible beyond L/W ＝4 (Sinha and Walton, 2019b).

The BBM was loaded in a realistic manner by following a load path from a calibrated continuum FLAC3Dmodel of the Creighton Mine.Appropriate input parameters for the BBM pillar model were ultimately determined by matching the displacements at six locations within the pillar to those measured in the field by a multipoint extensometer.After calibration, hypothetical load paths were tested to better understand how the pillar damage process was influenced by mining activities elsewhere in the mine.An alternate support pattern and an unsupported condition were also tested.Note that although some results of simulations on groundsupport interaction are presented,the primary goal of this study is to establish the integrated continuum-discontinuum approach.In the BBM, no pre-existing fractures were considered, as no prominent fractures were observed in the field(Walton et al.,2016);but it is possible to include the discrete fracture networks(DFNs)in BBM if necessary,as previously done by Preston et al.(2013),Farahmand et al.(2018),Vazaios et al.(2018),and Stavrou et al.(2019).In other words, the BBM in this study corresponds to an un-jointed pillar where yield progressed via intact rock damage.

Fig.1.Locations of the extensometers with respect to the different drifts and stopes(after Walton, 2014).The drift and stope numbers do not correspond to the depth of mining.All drifts and stopes were at the 7910 ft (2.4 km)level.The different numbers in brown (1-6) indicate the different stages of mining: (1) Mine-by or crossing of the 6330 drift face past the extensometer locations, (2) 6287 Crown blast, (3) 6336 Raise blast, (4) 6336 Blast 1, (5) 6336 Blast 2, and (6) 6336 Crown blast.

Polygonal BBM is one of the most common applications of discontinuum models and typically operates using Itasca’s Universal Distinct Element Code(UDEC).This approach represents a material domain as an aggregate of polygonal blocks(generated as a Voronoi Tessellation)that can detach once the contacts between the blocks are damaged.While the majority of the studies using the polygonal BBM approach have focused on the laboratory-scale rock fracturing process(e.g.Lan et al.,2010;Kazerani and Zhou,2010;Ghazvinian et al., 2014; Farahmand and Diederichs, 2015; Sinha and Walton,2020; Sinha et al., 2020), there has been some success in simulating field-scale behaviors as well (Christianson et al., 2006;Preston et al., 2013; Bai et al., 2016; Farahmand et al., 2018; Sinha and Walton, 2018a).

Perhaps the most relevant study is the one by Preston et al.(2013) who investigated the effect of pillar height on the ultimate strength.However, no support was considered and a constant velocity boundary was applied at the model edges to load the pillar.Bai et al.(2016)simulated a coal mine-entry housed in a water-rich environment using Voronoi BBM.Although Bai et al.(2016)considered supports in the form of rock bolts, cables, and steel strips, the model was restricted to the development loading stage(no production related loading).Other studies (e.g.Kaiser and Cai,2013; Xue and Mishra, 2015; Muaka et al., 2017; Kaiser, 2019)have developed excavation-scale models, but these were also limited by simplified loading conditions.In terms of reproducing displacements at multiple points as measured in situ, no BBM-based study has been successfully conducted yet in this regard.Therefore,this study is the first attempt to quantitatively reproduce field-measured displacements using BBM.

On the other hand, application of a load path from a 3D to 2D model (Shabanimashcool and Li, 2012) and coupling between continuum and discontinuum software, i.e.PFC2D-FLAC2D(Potyondy and Cundall, 2004; Cai et al., 2007; Saiang, 2010; Song and Hong, 2012; Zhang et al., 2017, 2019; Jia et al., 2018) and PFC3D-FLAC3D(Khazaei et al., 2015; Zhao et al., 2018; Qu et al.,2019), are not novel.In the case of PFC2D-FLAC2Dand PFC3DFLAC3Dcouplings, a region of the FLAC model is replaced by PFC elements,and there is a transfer of unbalanced forces between the two regions at each solution step.An active coupling between UDEC and FLAC3Dis not possible because of the difference in dimensionality.FLAC3DVersion 6.0 now allows coupling with 3DEC,but the large computational demand of 3D-BBM in 3DEC added to a mine-scale FLAC3Dmodel continues to be prohibitive for practical usage.In this study, some simplifications were made while integrating FLAC3Dand UDEC to ensure that the model’s runtime was acceptable while replicating the important aspects of the load path.

2.Integrated continuum-discontinuum approach-Model setup

Creighton Mine in Sudbury, Canada is one of the 10 deepest mines in the world with active mining depths extending to 2.5 km.The main orebody consists of nickel-copper mineralization along the contact between a felsic norite unit and the Huronian footwall rocks.Details of the geological environment and predominant structures at the Creighton Mine are provided in detail in the literature (Malek et al., 2008; Snelling et al., 2013).The particular location of interest in this study is the 7910 ft(2.4 km)level in the 461 orebody (Malek et al., 2009), which has 10 access drifts extending from a footwall drift (Fig.1).The granite in this area is relatively massive with rock quality designation (RQD) of nearly 100% and geological strength index (GSI) of approximately 75-85(Walton, 2014).

In November 2013,six multi-point extensometers(two clusters of three extensometers each)were installed in a pillar at the 7910 ft(2.4 km) level.The purpose of these extensometers was to record the deformations associated with mining activities, i.e.drift development, and extraction of stopes.Unfortunately, four out of the six extensometers (two in each cluster) were damaged during blasting, and deformation data could only be acquired from two extensometers.Although measurements from all six extensometers would have undoubtedly improved the data resolution, valuable information concerning the pillar behavior could still be obtained from the two functional extensometers.These two extensometers,termed E1 and E2(Fig.1),were 6.7 m and 6.9 m long,respectively,and were installed from the left side of the pillar(6300 drift),when the 6330 drift face was 7.5 m from E2.The locations of the six anchors of E2 are presented in the next section,while those of E1 can be found in Walton et al.(2016).The data from E1 were not used in this study as it was closer to the stope (larger out-of-plane movements) and exhibited time-dependent behavior due to the increased presence of sulphide minerals at this location (Walton et al., 2016).Each of the two extensometers operated for 258 d and recorded movements during 6300 and 6330 drift advancement and extraction of the 6287,6307,and 6336 stopes.More details on the excavation sequence and mining method followed at the Creighton Mine can be found in Walton et al.(2016).

The extensometer data were subsequently used by Walton et al.(2015, 2016) to calibrate a mine-scale FLAC3Dmodel of the Creighton Mine.Fig.2a shows the geometry and mesh size employed in this model (total model dimensions are L×W×H ＝220 m×160 m×70 m).In the study by Walton et al.(2016),a combination of the CWFS strength model and a mobilized dilation angle model was employed for modeling a 2.5 m region in the vicinity of the pillar, while a CWFS strength model with zero dilation was used in a region 150 m × 100 m × 40 m (L × W × H)centered on the pillar; regions further away from the area of interest were modeled as elastic.The orebody was modeled as perfectly plastic with input parameters from Ofoegbu and Curran(1992) and Vale (2013).Fixed displacement boundary conditions were imposed on all sides of the model,and pre-mining stresses of σ1＝ 96 MPa(E-W),σ2＝ 72 MPa(N-S),and σ3＝ 60 MPa(vertical),corresponding to in situ stress ratios of kE-W＝ 1.6 and kN-S＝ 1.2,were applied.It is important to note that the pillars at the site were supported by 75 mm shotcrete,mesh,and three rebar bolts(2 m of length)alongthe pillar height,but no such support was present in the FLAC3Dmodel.This means that the effect of support was implicitly considered in the derived rock mass parameters and the continuum nature of the model.The model was solved in 47 stages to mimic the excavation sequence at the Creighton Mine.

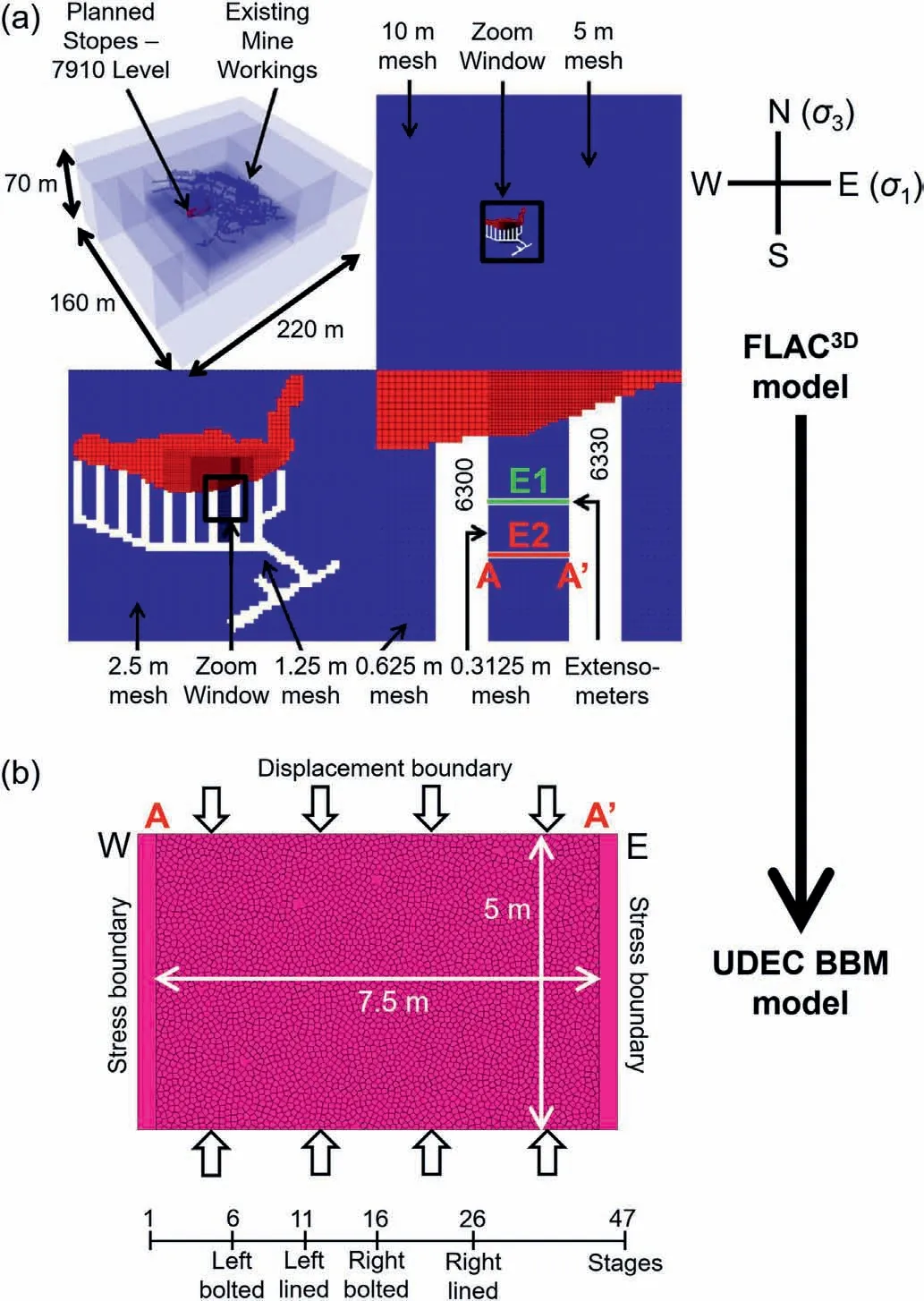
Fig.2.Schematic of the integrated continuum-discontinuum approach that shows (a)the mine-scale FLAC3D model (after Walton, 2014), and (b) the corresponding BBM pillar with dimensions and stages when supports were installed.

To constrain the model input parameters, the parameters were varied until the displacements in the model matched those measured by the two extensometers.Although data from only two extensometers were used, the ability of the model to match displacements at 12 different locations (anchors) over an extended period of time, combined with the fact that the input parameters were constrained using actual laboratory tests, provides a high degree of confidence in the model results.

Given the asymmetric manner in which the stopes were positioned with respect to the instrumented pillar in Fig.1a, one can expect the loads to not be purely vertical in nature but vary across the entire pillar width.Additionally,there will be some strain along the long axis of the pillar,but the magnitude can be expected to be relatively small away from the stope.As this problem is 3D in nature, in order to model the pillar in two dimensions, some simplifications are necessary.The complete modeling approach,including the methodology for transitioning from the FLAC3Dmodel to the 2D BBM, is as follows:

(1) It was decided to model a cross-section of the pillar (i.e.AA′in Fig.2a) that passes through the extensometer further away from the stope (E2).Accordingly, the magnitude of differential movements along the pillar length was less than those at the other extensometer location,as indicated by the results of the calibrated FLAC3Dmodel.

(2) Only the pillar was simulated in UDEC, as the focus of this

study is on the local discontinuum behavior of the pillar.The complex interaction between the host rock and the pillar wasconsidered in the FLAC3Dmodel and the corresponding boundary conditions applied to the UDEC model.The corresponding BBM pillar is shown in Fig.2b.

(3) In order to apply the same load path to the BBM as as experienced by the FLAC3Dpillar section AA′, a straincontrolled approach was adopted.In particular, the displacements (horizontal and vertical) along the top and bottom of the pillar were recorded for each of the 47 stages,and were applied to the BBM via a velocity boundary condition.Note that it is the difference between the displacements at two subsequent stages, instead of the raw displacement magnitudes at each stage,which was applied to the BBM as a velocity condition.

(4) To develop the BBM,the built-in Voronoi generator in UDEC with an edge length of 0.1 m was employed.This block size is considered to be small enough so as to not impose significant kinematic constraints on where fractures can develop within the model and also result in a manageable runtime(about 3 d for all 47 stages).Each block was also discretized using multiple constant-strain triangular zones.

(5) The zones in the BBM were much smaller than the zones in the FLAC3Dmodel (for comparison, FLAC3Dzones were 0.3125 m in size, which is more than three times the edge length of the BBM blocks).Therefore,the displacements from the FLAC3Dmodel could not be directly applied to the grid points(grid points are vertices of the zones)in the BBM pillar model.To resolve this issue, the addresses of all grid points along the top and bottom of the BBM pillar were extracted and classified into 25 groups, such that each group corresponds to half of the Cartesian space on either side of a grid point in the FLAC3Dmodel.This classification allowed the displacements from the all grid points in the FLAC3Dpillar slice to be correctly applied to the 25 groups of grid points in the BBM pillar model.

(6) Instead of directly applying the displacement differences(extracted from the FLAC3Dmodel)as a velocity in the BBM,it was scaled-up 10 times so that the model would need to be stepped only 0.1 s instead of 1 s to apply the appropriate displacements.It is important to note that the ‘time’in UDEC simulations is different from real time.For the current models, 0.1 s corresponded to approximately 111,170 time steps.Once the model was stepped by 0.1 s, the boundaries were fixed and then solved until mechanical equilibrium (a solution ratio of 10－5)was attained.This loading mechanism was repeated for all 47 stages.

(7) Prior to excavation of the drifts at the modeled section, a stress boundary condition was applied to the lateral edges of the BBM pillar.These stresses were also extracted from the FLAC3Dmodel and were applied through a layer of elastic continuum zones.The contacts between the elastic zones and the lateral edges of the BBM were made indestructible to facilitate a smooth transfer of stress.While the direct application of stresses to the BBM pillar boundary might seem to be a simpler alternative, it resulted in extensive cracking of the block contacts right from the start of the simulation(even when the drifts were not excavated past the AA′in the FLAC3Dmodel).The issue was related to the slight differential nature of the boundary stresses which were applied to the blocks along the pillar wall.

(8) As soon as the drifts were excavated, the stress boundaries were removed and replaced by three rock bolts with 2 m in length,and 19 mm in diameter.The rock bolts were modeled using cable structural elements (Gao et al., 2015; Bai et al.,2016; Shreedharan and Kulatilake, 2016).A shotcrete layer with 75 mm of thickness, modeled using beam structural elements, was also applied along the lateral boundaries of the model at pre-defined stages (see Fig.2 for the support installation timeline).

(9) The ‘spraying’ option in UDEC was employed for installing the shotcrete.For ‘spraying’, a central point from which the simulated spraying occurs and the angular extent of the region to be lined are specified, and UDEC installs the beam elements along the excavation periphery according to these parameters.To ensure that the shotcrete was uniformly applied along the entire pillar edge, all minor/partial blocks that dislodged during the initial loading process were manually deleted at Stage 11(left side of the pillar)and Stage 26 (right side of the pillar) prior to ‘spraying’.

(10) A constant out-of-plane (N-S) stress of 72 MPa (σ2; Walton et al., 2016) was applied to the BBM.Variations in stress along the pillar length might have some effect on the damage process in reality, especially at the later loading stages, but any such effects can at least be partially accounted for in the material parameters derived from the BBM calibration.To verify this assertion, a continuum model was run in UDEC(same setup as that in BBM,but only one block),and similar displacement profiles to those from the fully 3D model at AA′location could be obtained with slight parameter modifications.In particular,the peak cohesion and mobilized friction angle,as reported by Walton et al.(2016),had to be reduced by approximately 10%.

With all this in mind, the authors would like to highlight the difference in the loading mechanism in the FLAC3Dmodel and in the pillar BBM.The FLAC3Dmodel was actively perturbed by drift advancement and excavation of stopes which created unbalanced forces in the model.The BBM pillar, on the other hand, was perturbed by the equilibrium displacements of the FLAC3Dmodel and in a sense, lagged behind the FLAC3Dmodel at each stage.This is unavoidable as an active coupling between 2D and 3D models is not possible.

Fig.3 illustrates the complex nature of the load path applied to the BBM.The solid lines are the average displacements at each stage, while the error bars indicate the upper and lower bound magnitudes.A wider range of the error bars signifies a greater variability in the displacements applied to the pillar top or bottom.Interestingly, the variabilities in the displacements, especially the vertical ones, were found to increase in discrete increments following production blasts(refer to the excavation stages marked by black dotted lines in Fig.3a).Even more interesting is the fact that both the top and bottom edges of the pillar were subjected to significant horizontal movements which also happened to be in the same direction(Fig.3b).Horizontal displacements of both top and bottom edges are negative implying that the pillar was moving towards the left(West);this is intuitive,as the stopes were located to the left (West) of the instrumented pillar (Fig.1).Additionally,the differences in the magnitude of horizontal displacements along the bottom and top edge indicate that there was some shear loading on the pillar.This shear component increased rapidly following the 6287 Crown blast.Studies by Jessu et al.(2018) and Garza-Cruz et al.(2018) have shown how shear loading can destabilize rock pillars; it is, therefore, important to properly understand the loading mechanism at a site and assign realistic boundary conditions when attempting to model rock pillars.

3.Model calibration

With the integration of FLAC3Dand UDEC established, the next task was to identify a set of BBM input parameters that could reproduce the displacement profiles measured in the field(i.e.thedata from the extensometer located at AA′or E2).Before describing the calibration methodology, it is useful to review the different components of a BBM and the choices available in UDEC to represent these components.

As previously discussed, BBMs are composed of detachable blocks, and each block is discretized using finite-difference zones(Itasca, 2014).The interfaces between the blocks are called ‘contacts’and they operate through the Coulomb slip model.When the local tensile stress or shear stress on a contact exceeds its tensile or shear strength(defined by cohesion and friction angle),the contact is considered to be damaged.Zones can either be elastic or inelastic,depending on the constitutive model assigned to them.Elastic zones only require Young’s modulus (E) and Poisson’s ratio (ν) as input parameters, while appropriate strength and post-peak properties have to be defined for inelastic zones (e.g.cohesion,friction angle, tensile strength, and dilation angle).

An elastic BBM is the simplest model, has the least number of input parameters,and is relatively straightforward to adjust during calibration in terms of the relationships between input parameters and model outputs.Most large-scale studies to date have employed elastic zones in their simulations (Preston et al., 2013; Bai et al.,2016; Muaka et al., 2017; Farahmand et al., 2018; Wang et al.,2019; Bai and Tu, 2020).Given its wide acceptance, we started by using elastic zones in the BBM pillar.Initial calibration efforts indicated that it might not be possible to match the anchor displacements using this model,especially the anchors located deeper into the pillar.These models had pronounced damage along the pillar edges, but the contacts located deeper in pillar remained almost unaffected.An example is shown in Fig.4.This model corresponds to a contact cohesion of 39 MPa,contact tensile strength of 10 MPa, and contact friction angle of 27.5°which degraded to 21.3°upon failure.The different colors in Fig.4a correspond to the six anchors of the multi-point borehole extensometer(MPBX)and the positions of the anchors with respect to the pillar center are shown in Fig.4c.As can be seen,the model was able to replicate the displacements at the 3.15 m anchor location but there was no/minimal movement at the other anchor locations.The reason is the lack of fracturing deeper inside the pillar,as illustrated by the plot of failed contacts(Fig.4b).

It is known that microscopic heterogeneity or defects play an important role in the brittle rock damage process.Garza-Cruz et al.(2014) showed that when tensile strength heterogeneity was introduced in the contact properties, a high ratio of macroscopic uniaxial compressive strength to tensile strength(typical of brittle rocks) could be attained in elastic BBM.Following the same methodology, we randomly assigned the contacts tensile strength values from a Weibull distribution; the Weibull distribution parameters were based on a statistical fit to the laboratory tensile strength values of Creighton Granite(see Fig.5a).With the tensile strengths assigned stochastically, the cohesion was calculated following a constant ratio(cohesion/tensile strength),meaning that the cohesive strength also corresponded to a Weibull distribution.The contact friction angle was, however, homogeneous across the entire pillar, as implemented by Garza-Cruz et al.(2018).When selecting parameter combinations for model calibration, care was taken to ensure that the value of tensile strength (T) was always smaller than the Mohr-Coulomb theoretical upper limit of c/tan φ,where c and φ are the cohesion and friction angle, respectively.

As with the homogeneous and elastic representation, it was possible to identify a set of input parameters that could match the displacements at 3.15 m anchor location(Fig.5b).In particular,this model(termed ‘Model 1’)had a c/T ratio of 3.25 and a friction angle of 26°which degraded to 25°on failure.A significant mismatch in displacements was observed at all other anchor locations and this can again be attributed to the lack of contact damage deeper inside the pillar.If the contact strengths were lowered to induce damage near the pillar center, then the peripheral displacements were extremely large.To demonstrate this,the results for another model(termed ‘Model 2’) calibrated to the 2.45 m of anchor is shown in Fig.5b.Clearly, it is not possible to reproduce the displacement profiles at all anchor locations using an elastic block model.

A convenient alternative is to use an inelastic constitutive model in the zones.There are two benefits:(1)the model runtime does not increase drastically, and (2) zone yield can simulate the finer-scale cracking deeper within the pillar where contact damage is suppressed by large confining stresses.The damage along the pillar periphery, however, can still be explicitly simulated by contact failures and block separations.A continuum approximation of the damage development within the pillar is acceptable as long as the deformations are not significant(i.e.the process is not macroscopically discontinuous).The key to the successful implementation of this approach is the selection of zone and contact input parameters such that irreversible damage occurs primarily via contact failure along the periphery and zone yield within the pillar.

In this study, we assigned the CWFS model and Walton-Diederichs mobilized dilation model (WD; Walton and Diederichs, 2015) to the zones, similar to the approach used for the entire pillar by Walton et al.(2015, 2016).The strength and dilation model parameters were initially chosen from Walton et al.(2016) but were varied to match the displacement profiles.Responses of inelastic models are mesh-dependent and it is sometimes necessary to modify the parameters when the mesh size is changed.

Fig.3.(a)Vertical and(b)Horizontal displacement paths applied to the top and bottom edges of the BBM pillar model.“Mine-by”in(a)corresponds to the date on which the 6330 drift face crossed the extensometer location.

The contacts were defined using peak and residual cohesions(cpeakand cres), peak and residual friction angles (φpeakand φres),and tensile strength (σt).The physical meaning of the individual contact parameters is not as straightforward as assumed.For example,one might expect the φresto be related to the basic friction angle(Alejano et al.,2012)in some fashion,but BBM behaviors are heavily influenced by the geometric interlocking of the blocks,and consequently much smaller values of φresare typically required to obtain reasonable results (Christianson et al., 2006; Farahmand et al., 2018; Stavrou and Murphy, 2018; Dadashzadeh, 2020).As a result, the contact properties in this study were calibrated based purely on the capability of the model to match the field displacements.For support elements, the shotcrete properties in Chryssanthakis et al.(1997) and Malmgren and Norlund (2008)were used in the initial model, while those in Bahrani and Hadjigeorgiou (2017) and Zipf (2006) were referred to for determining the cable properties;ultimately,these were also varied as a part of the model calibration process.

As the contact properties had the greatest degree of uncertainty,these were modified over a much wider range that the others.For this type of BBM application, there is no well-established calibration methodology.A trial and error approach was used, and the greatest confidence was placed on the support and zone input parameters (meaning these were modified least from their initial values).The ranges over which the different parameters were modified in this study are as follows: (a) Contact-peak cohesion:30-70 MPa, peak friction angle: 0°-50°, residual friction angle:0°-30°, tensile strength: 8-12 MPa; (b) Zones-peak cohesion:40-55 MPa,mobilized friction angle:40°-50°,tensile strength:8-14 MPa, plastic shear strain from peak to residual (or initial to mobilized): 0.005-0.025; (c) Shotcrete-modulus: 15-25 GPa,compressive strength: 25-40 MPa; (d) Cable-stiffness of grout:400-2000 MN/m/m.In BBM, due to block wedging, contacts are more prone to failure than the zones within the blocks;accordingly,values of contact cohesion greater than those of the zone cohesion were tested.Modifications to zone dilation parameters were also tested as a part of the calibration process,but ultimately those from Walton et al.(2016) were used.

During the back-analysis process, some unusual trends were noted.If the strengths of zones were too large, the model displacements increased drastically at the outer anchor locations.This may be due to block movements contributing more towards the pillar displacements.Secondly, it was found difficult to control the displacement profiles by making small systematic changes to the input parameters.For example, when the contact cohesion was increased from 45.2 MPa to 45.3 MPa, the deformation at the outer anchors did not decrease.The behaviors were, however, consistent with expectation when large changes were introduced (e.g.from 45 MPa to 47 MPa).A closer look into the model results revealed interaction between the fractured contacts and the yielded zones, which modified the locations of the damaged regions, thus impacting the model results in an unpredictable way.

During the model calibration phase, the authors identified a number of input parameter sets that produced similar data-model fits.Four such results are shown in Fig.6, termed ‘Calibrated’,‘Alternative 1’, ‘Alternative 2’, and ‘Alternative 3’, respectively.The only differences in the parameters for the three alternate models with respect to the Calibrated model (Table 1) are presented in Table 2.Some of the differences in these model parameters are very small(cpeakof 0.05 MPa and φresof 0.2°)and they affected different aspects of the data-model fit, further exemplifying the unpredictable influences of small parameter changes.Note that although the data from the MPBX is one-dimensional (1D) in nature, displacement measurements corresponding to six different locations over 47 different stages were considered in this study.Agreement with such a large amount of data helps to establish the reliability of these models.

The four parameter sets have different strengths and drawbacks with respect to their representation of specific pillar displacement behaviors.Alterative 1 replicates the displacements of the outermost anchors well,but the mismatch for the 2.45 m anchor is large.Alternatives 2 and 3 replicate the displacements at all anchors except for the 3.15 m one.The Calibrated model represents a balance between the two extremes.It captures the displacements at all anchors fairly well but slightly overestimates the 2.45 m anchor displacement(errors are on the order of around 1 mm)at the early phases of loading.Despite numerous trials, the 2.45 m anchor displacements could not be reduced any further without affecting the data-model fit for the other anchor locations.Ultimately, the authors decided to use the Calibrated model to conduct the rest of the study.

Fig.4.(a) Displacement profiles at different MPBX anchor locations compared to the field measurements, (b) location of failed contacts at the Stage 47, and (c) location of the six anchors of the extensometer with respect to the center of the pillar.All displacements are reported with respect to the center of the pillar (i.e.the center of the pillar had no displacement in this representation).

Fig.5.(a)Weibull distribution fitted to laboratory tensile strengths of Creighton Granite,and(b)displacement profiles at the different anchor locations in Models 1 and 2 compared to the field measurements.

4.Calibrated model results

Fig.7a shows the vertical stress contours and damaged contacts for the Calibrated model after the Stage 47.The presence of elongated, axial cracks along the periphery is readily evident.As one moves towards the center,the intensity of fractures reduces and is almost negligible at 2 m into the pillar.Due to extensive cracking,there was also a loss of load bearing capacity of the pillar periphery,which pushed the stresses deeper into the pillar (called as ‘core’).This boundary-relaxation-core-formation process in pillars was observed by Wagner(1974)in the field.It is interesting to note the asymmetric shape of the de-confined region on either side of the pillar(see Fig.7b).The more severe damage on the left side is likely because of the stope being located to the left of the pillar and the left drift(i.e.Drift 6300)being developed earlier than the right one(i.e.Drift 6330).

Within the stressed core, all contacts were subjected to large compressive normal forces (as high as 6 MN in Stage 47), and this reduced the likelihood of any tensile or shear failures.The damage process at this point must be controlled mainly by the zone yield,which in this case represented finer-scale micro-cracking (or low dilatant shearing).Such a change in failure characteristics as a function of position within the pillar was reported in the literature(Chen,1993; Esterhuizen and Ellenberger, 2007; Kang et al., 2015;Bai et al.,2019;Li et al.,2019).For the Calibrated model,the extent of plastic yield at the Stage 47 is shown in Fig.7c.Similar plastic yield plots for other mining stages as well as for Alternatives 1-3 can be found in the Appendix B.Firstly,it can be observed that there was minimal zone yield at the periphery of the pillar, where extensive contact damage existed(see Fig.7a).Secondly,zone yield occurred across the entire diagonal of the model and included regions within the confined core.A cross-shear shape of the yielded zone in slender pillar can also be found in the continuum simulations of Sinha and Walton (2018b).The shape is not perfectly symmetrical in this case due to the complex load path applied to the pillar.

A closer look at the model results revealed an interesting damage mechanism-it is not the contacts along the periphery that were damaged first but the zones at the pillar corners (see the highly damaged green regions in Fig.7c).This phenomenon was also observed by Chen (1993) in brittle potash pillars.The zone yield perturbs the stress field along the pillar periphery in a complex manner that allows contacts deeper within the pillar to undergo damage.This mechanism was verified by analyzing the plastic shear strain contours and fractured contacts at each stage.Note that although the zone yield modified the stress field to some extent,the damage was mainly via contact failure at the outermost anchor locations (see Fig.7a and c).

It is important to track the evolution of pillar stresses to identify the load state on a complete stress-strain curve.For this, the vertical stresses were averaged over all zones in the model for each of the 47 stages and are plotted in Fig.8.The evolution of fractured contacts in the BBM is also shown for three particular stages.At Stage 8, distributed fractures can be seen to develop along the left(West) pillar edge (prior to ‘Mine-by’); at this stage, the stress boundary was still present on the right margin.Subsequently following the ‘Mine-by’, fracturing was induced near the right(East) pillar boundary, and some of the previously disconnected fractures coalesced along the left (West) pillar boundary.This suggests that the strength of the rock mass was likely reduced locally.With further loading due to mining activities, the intensity of failed contacts increased along both edges of the pillar.Similar progressive brittle damage or slabbing with formation of axial cracks along the pillar edge after ‘Mine-by’ has also been reported in other studies(e.g.Gendzwill and Stead,1992;Chen,1993;Lajtai et al.,1994; Maybee, 2000; Styles et al., 2010).

From Fig.3a, it is easy to perceive the monotonic nature of the vertical strain path applied to the pillar.This in turn implies that the drop in the average vertical stress in Fig.8 is a result of mininginduced damage, instead of a reduction in strain.The peak vertical stress attained during the loading process,i.e.pillar strength,is 90.4 MPa for the Creighton BBM.Interestingly, the strength predicted by the Hedley-Grant equation(Hedley and Grant,1972)for a 7.5 m of width, 5 m of height quartzite pillar (the equation was based on quartzite pillar case studies)is 108.9 MPa.If this strength is normalized to the intact uniaxial compressive strength of the host rock, then one obtains 108.9/230 ＝0.47.For the Creighton pillar BBM, the ratio of the peak strength to the intact uniaxial compressive strength is 90.4/200 ＝0.45,which is within 5%of the value predicted by the Hedley-Grant equation.This agreement in strength value was not a goal of the calibration process,but rather arose as an emergent behavior from the model after calibration to the displacement results.The peak strength is a reflection of load capacity in the vertical direction (perpendicular to the MPBX orientation), and the agreement in strength therefore increases confidence in the model results relative to the displacement-based calibration which relied on purely 1D data.

The original database of Hedley and Grant(1972) includes only long pillars, and it is known that longer pillars are generally stronger(Dolinar and Esterhuizen,2007;Sinha and Walton,2019b).The Hedley-Grant equation, therefore, includes the additional strengthening effect of length.The particular Creighton pillar being modeled in this case is also long, with an L/W of around 3.75.As discussed in Section 1,the pillar strengthening effect due to length flatten out beyond L/W ＝4 (Dolinar and Esterhuizen, 2007; Sinha and Walton, 2019b) and this permits the 2D BBM, which assumesa plane-strain condition and effectively simulates an infinitely long pillar, to attain a pillar strength consistent with that from the Hedley-Grant equation.

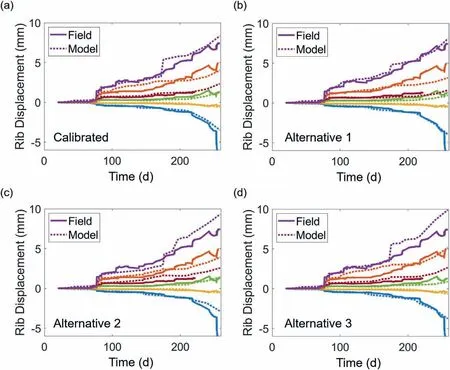
Fig.6.Comparisons of field-measured and model-predicted displacement profiles for (a) Calibrated, (b) Alternative 1, (c) Alternative 2, and (d) Alternative 3 models.

Table 1Input properties of zones, contacts, shotcrete and bolts for the Calibrated model.

Post-peak, the pillar starts to lose its load bearing capacity gradually, and by the time Stage 47 was reached, the stresses had reduced by 20%.Contrary to the BBM,the FLAC3Dmodel exhibited a slightly different trend (a comparison of the stresses predicted by these two models is presented in Appendix A).It is well-establishedthat the response of a pillar transitions from brittle to ductile as the W/H is increased (Mortazavi et al., 2009; Esterhuizen et al., 2010;Sinha and Walton,2018b; Li et al.,2019).For hard-rock pillars,the transition point has been found to be around W/H ＝2 (Mortazavi et al., 2009; Sinha and Walton, 2018b).As the simulated pillar is below this transition point, a softening response is naturally expected.Of particular importance in this regard is the capacity of the pillar to bear large load levels beyond its peak strength.Current pillar design techniques only incorporate the peak strength in the design process but neglect the post-peak load bearing capacity of pillars.If the residual load bearing capacity is considered in the design process, then it may be possible to reduce/optimize pillar dimensions.It is of course necessary to improve our understanding of the post-peak behavior before it can be implemented in the design process.

Table 2Input parameters that are dissimilar in the Calibrated model and the Alternative models.

5.Analyzing the effect of support

With the reliability of the Calibrated BBM established, this model was then used to examine the effect of alternate support patterns on the model response.Although this research is interesting and can provide valuable insights into the rock-support interaction mechanism, it will be dealt with briefly in this study.Our intent is not to optimize support design for the Creighton Mine,but rather to demonstrate a procedure so that future studies coulddevelop site-specific BBM and test multiple support combinations to optimize support at the site.

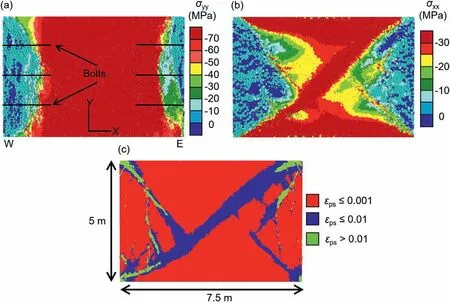
Fig.7.(a)Vertical stress contours,(b)horizontal stress contours,and(c)plastic yield contours in the Calibrated model at Stage 47.εps is the plastic shear strain which is a proxy of damage.

We tested two alternate support conditions-Unsupported (no support in the model) and 5 bolts ＋shotcrete.Compared to the support pattern at the site (i.e.3 bolts ＋shotcrete), these two support conditions should encompass a wide range of ground behaviors.The locations of the bolts in the 3 bolts ＋shotcrete layout and the 5 bolts ＋shotcrete layout are shown in Fig.9a.Of particular relevance here is to revisit the FLAC3Dsupported and unsupported model results of Walton et al.(2016).In that study,the effect of rock bolts and shotcrete was simulated using equivalent support pressures of 250 kPa and 1.5 MPa,respectively,following the guidelines of Hoek(1999).It can be seen in Walton et al.(2016)that the model displacements with and without supports did not differ by more than 1 mm(at all anchor locations).Sinha and Walton(2019a)also highlighted this drawback (underestimation of support effect) of continuum models using hypothetical granite pillar models and a coal pillar model.The practical implication of this finding is that continuum models are not well suited for designing rock reinforcement in terms of its influence on ground behavior.

While there are no field data available to establish the realism of the deformations in the unsupported and 5 bolts ＋shotcrete BBMs,it can at least be expected that the deformations will increase and decrease non-negligibly compared to the 3 bolts ＋shotcrete condition (unlike in the FLAC3Dmodel).If such results are indeed obtained,it will qualitatively demonstrate the potential of BBM to be used as a support design tool.Nevertheless, further studies are required to assess if BBM can also capture the finer-scale interaction between support and a deforming rock mass.

To identify the effect of support in the current BBM, it was decided to extract the horizontal displacements of grid points spaced at 0.1 m along the vertical edges of the pillar.This is a direct approach to evaluate the support effects since the displacements at pillar walls are aggregations of the movements occurring across the entire pillar.In mining environment, displacements on the pillar walls are also used to identify impending instabilities or the need for additional support.For that purpose, the locations of the grid points were extracted in the pre-cycling condition (i.e.before running the model), and the corresponding horizontal displacements for Stage 47 are shown in Fig.9b.

Fig.8.Average stress in the pillar models as a function of stage number.

A reduction in deformation with increasing support density is apparent in Fig.9b.Note the asymmetric nature of displacements along the pillar height caused by the differential loading along the top and bottom edges of the pillar.While one would expect the deformation profiles with increasing support density to be similar in shape but translate towards lesser magnitudes, this is certainly not the case in Fig.9b.The greatest degree of displacement reduction was observed along the bottom left corner of the pillar,where the displacements dropped from 27 mm under unsupported conditions to 17 mm in the Calibrated model.This change(drop by 37%) is much more significant than that simulated using a continuum model.

Some other trends in Fig.9b can be observed:

(1) At the top left corner,the displacements in the unsupported and Calibrated model are similar.The 5 bolts ＋shotcrete model, however, predicted more than 5 mm less displacements at this location.The lack of difference in displacements between the Calibrated and unsupported model is related to the greater depth of fracturing in the former one and the absence of support in the latter.This will be discussed further below in the context of the displacement results shown in Fig.10.

Fig.9.(a)Locations of the bolts in the 3 bolts/calibrated layout and the 5 bolts ＋shotcrete layout,and(b)horizontal displacements along the edges of pillars for three support cases.

(2) The addition of 2 extra bolts did not have a significant effect on the displacements at the bottom left region of the pillar.It appears that the bottom rock bolt in the Calibrated model was able to efficiently suppress the deformations around this region without the addition of further support.

(3) The simulated displacements reduced systematically from unsupported to 3 bolts ＋ shotcrete to 5 bolts ＋ shotcrete conditions along the right pillar edge up to around 1.5 m from the pillar bottom.

(4) The change in displacements along the lower 1.5 m of the pillar right edge is minimal,as fracturing was insignificant at this location.

From these results,it is clear that the 5 bolts ＋shotcrete system performs better in suppressing surficial movements.

Fig.10 shows the displacement contours for the unsupported, 3 bolts ＋ shotcrete and 5 bolts ＋ shotcrete conditions at Stage 47.It is interesting to note the difference in the damaged high displacement region along the left edge of the pillar in the 3 bolts ＋shotcrete case versus the unsupported and 5 bolts ＋shotcrete cases.For the 3 bolts ＋ shotcrete case, the regions of ‘＜ －10 mm’ and ‘＜ －20 mm’extended much deeper into the pillar than those in the other two models (more than 0.5 m for the ‘＜ －20 mm’ region).Such a deep damage region did not exist in the 5 bolt ＋shotcrete case due to the presence of bolts closer to the top and bottom edges of the pillar.These bolts stiffened the rock mass at the corners and prevent the propagation of damage deeper into the pillar.In the 3 bolts ＋shotcrete case, the outer bolts were further away from the top and bottom edges of the pillar; accordingly, the region around the center of the shallow fracture zone was stiffened,but this pushed the damaged zone deeper into the pillar, leading to larger pillar boundary displacements.The thinner high displacement region on the left side of the unsupported model can be explained by the lack of support-induced stiffness in the system.The damage that initiated at the corners in the unsupported model had more kinematic freedom to propagate along the pillar surface.To further verify that the variations in the damaged region are indeed related to the positions of the outer bolts,another 3 bolts ＋shotcrete model was run,with the outer bolts installed at the same location as those in the 5 bolts ＋shotcrete case.From Fig.10,it can be seen that the depth of damaged region reduced significantly and is similar to that in the 5 bolts ＋shotcrete case.These results indicate that the interaction between unsupported rock and support can be quite complex, and positions of the supports can locally modify the depth of the damaged region.

When the displacements on the left edge of the pillar in the unsupported and 5 bolts ＋shotcrete cases are compared, one can discern the similarity in the shape of the high displacement regions(i.e.‘＞15 mm’ in the 5 bolts ＋ shotcrete case and ‘＞20 mm’ in the unsupported case).Only a reduction in the magnitude of displacement in this region signifies the clamping effect generated by the rock bolts(pinning the fractured slab to the pillar core).On the right edge,the high displacement regions were significantly suppressed in the 5 bolts ＋shotcrete case owing to its higher support density.There was only minor fracturing along the bottom right corner of the pillar(Fig.7a),and this is likely the reason why the displacements for all three support cases were similar in this region in Fig.10.Lastly,it can be seen that the spatial extent of the ‘＞20 mm’region declined systematically with increase in support and this establishes the capability of BBM in reproducing the support effect.

The difference in deformation between reinforced ground and unreinforced ground should become more apparent as the intensity of damage increases.In other words, as a pillar is continuously strained, new stress-fractures will be formed along the edge and the existing stress-fractures will continue to separate.If a bolt is structurally intact at this point, it would resist the deformations and suppress the volumetric bulking of the pillar.Consequently,the lateral deformations along supported and unsupported pillar edges would diverge as the pillar is subjected to a higher level of load.

This was tested in the current BBM by increasing the load along the model top and bottom,following two hypothetical schemes.In the first scheme (termed “H and V”), the horizontal and vertical displacement increments for Stage 47 were applied to the model boundaries for 40 times while bringing the model to a static equilibrium after each increment.In the second one(termed“only V”), only the vertical boundary displacement increments were applied while fixing the horizontal boundary displacements.Both the unsupported and 3 bolt ＋shotcrete (Calibrated) cases were tested, and the resulting horizontal displacement contours at the end of the 87th stages (47 ＋ 40 ＝ 87) are shown in Fig.11.

As expected, the discrepancies in deformations in the unsupported and 3 bolts ＋shotcrete models increased for both loading schemes.For the ‘H and V’scheme,although the ‘－40 to －60 mm’region continued to be larger in the 3 bolts ＋shotcrete case, the displacements were suppressed along the bottom left by over 50%.A growth in the extent of‘＞40 mm’displacement region can also be observed along the right edge.For the ‘V’loading scheme,a similar behavior was noted but with significant additional increase in the‘＞40 mm’and ‘＞60 mm’regions along the right edge.Because the horizontal boundary displacement increments were not considered in the ‘V’ scheme, the contour patterns became symmetrical.

6.Analyzing the effect of hypothetical load paths

The response of numerical model is heavily dependent on the applied boundary conditions.In order to use such models to simulate the behavior of underground structures,it is important to assign a load path in accordance to the way in which the structure isloaded in reality.It has been illustrated in Section 2 how the Creighton pillar slice was subjected to both non-uniform vertical displacements as well as horizontal shear along the top and bottom edges.To highlight the importance of assigning a realistic boundary condition while modeling rock pillars, we re-ran the Calibrated model but only with vertical displacement increments.The focus understandably is on the presence of horizontal shear movements along the edges of the pillar, which has been neglected in many previous pillar-oriented studies.This scheme is similar to that in the last section(‘V’scheme),with the key difference being that the vertical load path in this scheme was applied right from the start of the simulation rather than after Stage 47.

Fig.12a shows the horizontal displacement contour after Stage 47.As can be seen, the damaged regions became much more symmetric and localized when the model was loaded via vertical displacement increments only.In particular, the depth of‘＜－20 mm’ region markedly reduced (approximately 0.5 m), and the overall magnitudes were lower as well (see Fig.12a).The displacements along the right edge, however, increased; this can be identified by comparing the 20 mm displacement contours in Figs.10 and 12a.It seems that the presence of horizontal displacements along pillar edges can disproportionately damage two opposite walls of a pillar.For the current BBM, the displacement magnitudes as well as the extent of the damaged region shifted notably when the shear movements along the model top and bottom were omitted.One must therefore pay particular attention to boundary conditions when using numerical models to estimate support needs (i.e.volume of bulked material).A practical implication of these results is that support requirements on either side of a pillar might differ, depending on its location with respect to the stopes.

In addition to testing the effect of shear load on a pillar,we also investigated how the shallow damage process might be influenced by a loading-unloading cycle.This investigation is of particular relevance to block cave mining, where a pillar (e.g.between the undercut and draw levels in block caving mines) might undergo cyclic loading during the caving process (Garza-Cruz et al., 2014).Two different load paths were tested to accomplish this goal (see Fig.12b).The horizontal component of the displacement increments was still neglected in the BBM to simplify the analysis.

Path 1 is an unloading-loading scheme,where the vertical strain was first lowered by 0.00035 at Stage 47, solved to equilibrium,then raised by 0.00035 and re-equilibrated.The idea behind testing an unloading-loading path was to understand if additional damage can occur even when the pillar is not monotonically loaded.Path 2 is a loading-unloading scheme, opposite to Path 1.To increase or decrease the applied vertical strain,the displacement increments at Stage 47 were multiplied by constant factors with the appropriate sign.This means that all the individual vertical displacement increments along the top and bottom edges were increased or decreased by the same proportion.

The horizontal displacements corresponding to the final state of the simulations with loading Paths 1 and 2 are shown in Fig.12c and d.It can be observed that even when the pillar is not exposed to a higher maximum strain, damage can still be induced by an unloading-loading cycle(Path 1).This is evident along both the left and right edges of the model (Fig.12c).When the pillar is overstrained (Path 2) instead, the displacements along both edges increase drastically (＞30%; Fig.12d).Such a behavior is intuitive, as additional load would fail more contacts along the pillar boundaries,resulting in more bulking.A loading-unloading cycle during production activities(e.g.caving),therefore,might have the potential to severely damage a pillar and increase the strain on the pillar support.

When developing the cycling loading schemes in the BBM,some alternate load paths were also tested.Interesting results were obtained when theloading-unloading wasconducted ina more gradual/stepwise manner at an earlier model stage (Stage 30).It was found that the damage and bulking were less significant in this model in comparison to a model subjected to a sudden loading-unloading path(i.e.Path 2).Such a differencewasnot noted at Stage 47,which islikely due to the rock mass already being substantially damaged at this point.This is interesting in the sense that it can be tied to real time excavation sequencing.If the production activities are designed so that the rock mass(relatively undamaged at this point)is allowed to equilibrate before the next blast, then the severity of rock damage could be minimized.The time for a rock mass to stabilize after loading will of course vary from one mining site to another.

The effect of loading-unloading on pillar was previously investigated by Garza Cruz et al.(2014)in 3DEC using elastic,tetrahedral blocks.In terms of the model findings,the key difference is that thebulking and the extent of the damaged zone were affected more during the unloading phase in Garza-Cruz et al.(2014),while in our study, the effect was found to be more pronounced in the loading(or re-loading) phase.Although the models in Garza Cruz et al.(2014) were unsupported, the potential for the presence of support causing this difference was ruled out by running Paths 1 and 2 under unsupported conditions, which yielded similar results.The exact cause of the discrepancy is not well understood and could be attributed to a number of factors, including different loadingunloading mechanisms in Garza Cruz et al.(2014) and in this study, differences in the degree of rock mass damage prior to unloading, and differences in block shapes and zone representations.

Fig.10.Horizontal displacement contours for the unsupported,3 bolts ＋ shotcrete,5 bolts ＋ shotcrete,and 3 bolts ＋ shotcrete with the outer bolts further away from the center of the pillar cases at Stage 47.

Fig.11.Horizontal displacement contours for the unsupported and 3 bolts ＋shotcrete cases after 40 additional stages with two different loading schemes (H indicates horizontal and V indicates vertical).

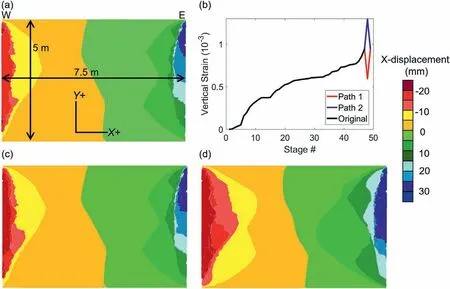
Fig.12.(a) Horizontal displacement contours in BBM with vertical displacement increment boundary at Stage 47, (b) original and 2 alternate vertical strain paths (Paths 1 and 2)tested on the BBM pillar, horizontal displacement contours in BBM after (c) Path 1, and (d) Path 2.

7.Conclusions

This study has presented an integrated 3D continuum-2D discontinuum modeling approach to assist in the use of 2D BBM for studying 3D mining problems.In particular, the load path from a calibrated mine-scale FLAC3Dmodel was applied to the BBM to simulate the damage process in a rock pillar (slice of pillar) in the Creighton Mine,Sudbury,Canada.Pillar support in the form of rock bolts and shotcrete was also considered.The discontinuum pillar model was ultimately calibrated by matching the displacements in the model with the MPBX extensometer measurements made at the site.

Post-calibration, two different support conditions were tested-unsupported and 5 bolts ＋shotcrete(the pillar at the site was supported by 3 bolts ＋shotcrete).A significant decrease in the lateral deformation along the edge of the pillar was noted as the support density was increased.Additionally, there was an interaction between the load path applied to the BBM and the supports that led to non-uniform deformation changes along the height of the pillar.It was concluded that the location of rock bolts can affect the extent of damage and magnitude of bulking along a pillar edge.The effect of shear movements along the pillar top and bottom boundaries was subsequently assessed.It was found that shear loading can disproportionately damage the two vertical edges of apillar.Lastly,to understand how caving-induced loading-unloading can affect pillar behavior, two different load paths were tested.Loading-unloading resulted in greater shallow damage than unloading-loading did.Although the pillar was not over-strained during the unloading-loading scheme, it still resulted in some additional cracking along the pillar edge.In future,with advances in computational capacity, a similar integrated study could be conducted with coupled FLAC3D-PFC3Dor FLAC3D-3DEC model to better represent the 3D damage process in rock pillars.

Declaration of competing interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgments

The research conducted for this study was funded by the National Institute for Occupational Safety and Health (NIOSH) under Grant No.200-2016-90154.The authors would like to extend their gratitude for the financial support.Special thanks to Dr.Mark Larson and Dr.Bo-Hyun Kim for reviewing this manuscript prior to submission and providing valuable suggestions.The modeling effort for this study was conducted using educational licenses of UDEC provided by Itasca Consulting, Ltd.The authors appreciate Itasca’s support in this capacity.

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2020.06.011.