基于工业物联网的混流车间机器人自适应调度

郭 剑，史耀耀，胡 昊，陈 振，张军锋，赵 盼

（1.西北工业大学机电学院，西安 710072；2.西北工业大学航空发动机高性能制造工业和信息化部重点实验室，西安 710072；3.西安建筑科技大学机电工程学院，西安 710055）

随着计算机技术、传感器技术、无线通信技术和机器人技术快速发展，制造业正向高度自动化和智能化方向发展[1]。自新冠肺炎全球蔓延以来，5G技术、大数据中心、工业物联网、人工智能和机器人技术在“抗疫”中发挥了极大作用，力促我国加速工业“新基建”的投入。在这一背景下，企业将大量使用移动机器人和自动导引运输车(Automated guided vehicle,AGV)进行车间调度和仓库物料配送，实现智能化生产和供应链管理[2]。

当前，制造企业面临着激烈的市场竞争和不断上升的制造成本等方面的挑战，同时产品需求频繁波动也给企业带来较大压力[3]。而物料调度不仅能够优化完工时间，同时在遵从客户需求下能够找到设备、路径和运送时间等的最佳组合。近几年国内外对于物料机器人调度方面的研究主要集中于传统静态调度问题，即在所有信息稳定且已知的情况下通过启发算法求解。朱琳等[4]提出了一种改进的遗传算法进行自动导航小车的任务分配和任务排序优化。Mousavi等[5]结合遗传算法和粒子群算法优化柔性车间中的多目标AGV调度问题。Gen等[6]以最小完工时间为优化目标，应用基于混合优先级的遗传算法求解AGV调度问题。Jerald等[7]提出自适应的遗传算法和蚁群算法，以实现AGV调度中的综合惩罚成本和机器空闲时间的最小化。Batur等[8]在两种邻域结构下应用模拟退火启发算法求解混流车间(Hybrid flow shop,HFS)中的物料机器人调度问题，并通过对比验证了该方法的有效性。Zabihzadeh等[9]应用双信息素的蚁群算法和遗传算法分别优化混流车间中多物料机器人调度问题，结果表明遗传算法性能更优。然而，在实际生产中，难以提前获知所有加工任务信息，并且在动态的车间环境中存在诸多不确定信息（如紧急任务，设备故障，任务返工等），因此难以将静态调度用于实际生产中。

近年来，由于无线射频识别和条形码等工业物联网技术已逐步扩展到制造环境中，车间实时数据经多源数据融合处理后形成制造业的大数据环境[10]。而这些来自各种传感器的实时数据流并不能直接适用于传统的物料处理系统，因此，越来越多的学者开始关注物料机器人实时调度问题，以解决运行环境中动态调度问题。Lee等[11]指出在实时数据环境下，制造系统中的物料处理系统将更加高效。Zhang等[12]基于AGV实时状态提出物料运送的优先策略用于物料调度。Li等[13]提出了同时面临多个客户需求时的智能仓库系统AGV调度机制。研究表明，在车间调度中使用多种调度规则(Multiple scheduling rules,MSRs)比使用单一调度规则能更大程度地提高生产效率[14]，刘想德[15]应用层次分析法(Analytic hierarchy process,AHP)在组合规则中选择调度规则，避免了传统调度人员在制定调度方案时凭借经验或自己偏好选择调度规则。上述文献中，多在实时环境下应用先进先出(First come first served，FCFS),最短距离(Shortest distance first，SDF)和最早截止时间 (Earliest due date first，EDD)等规则调度物料机器人，或基于传统知识库选择规则，因此实时适应性较差。

为解决上述问题，越来越多的学者开始应用强化学习算法求解车间物料调度问题。Wang[16]提出基于加权的强化学习车间自适应调度方法，通过聚类和动态搜索确定适合策略。另外Zhang等[17]通过融合遥感信息和AGV信息实时共享，并优化AGV速度避免碰撞，同时提出紧急任务超车策略实现AGV调度。Shahrabi等[18]引入带有Q因子的强化学习算法以提高动态车间调度性能，仿真结果表明该方法相比传统单规则调度和邻域搜索，优化性能较高。

尽管上述文献中物料机器人调度研究取得了一些研究成果，但考虑到在工业物联网下车间调度属于复杂的实时优化问题，且鲜有涉及大批量和多种类任务的动态混流车间调度问题的相关研究。因此本文提出应用SP–MCTS的机器人自适应调度方法，是在基于工业物联网的混流车间中以最小化完工时间和延迟率为优化目标，将调度系统实时信息作为输入状态，通过搜索学习快速选出实时状态下适应的调度规则和机器人，然后发送调度指令进行工件运送。最后通过模拟试验对所提方法进行分析评估，验证其可靠性和有效性。

混流车间中物料调度问题

混流车间中物料机器人的调度问题可以描述为：多组工件je={1，2，…，ne}需经Oj1→Oj2→，…，→Ojs道工序加工。每道工序S={1，2，…，s}内有Mk≥1个同类并行设备，且工件j只能占用工序内一台平行设备加工。R个机器人对线内物料进行卸载、运送、装载。由于各工序间不设缓冲工位，物料完成加工后将在设备上等待运送，因此当阻塞发生时机器人选择运送工件的实时调度策略尤为重要。如图1所示，物料运送过程满足以下约束：（1）开始调度时，各组内的工件释放时间相同；（2）工件j在每道工序只能加工一次，且每台设备同一时刻只能加工一个工件；（3）工件在占用每台设备的时间由两部分组成，即加工时间和等待运送时间；（4）物料的运输时间由设备的距离决定。

为模型建立需要，引入参数变量用于描述数学模型，见表1。

混流车间实时调度是依据实时状态选择规则，然后按照规则在车间约束关系下选择运送物料的方法，因此混流车间中物料运送的约束关系如下[19]：

即

s.t．

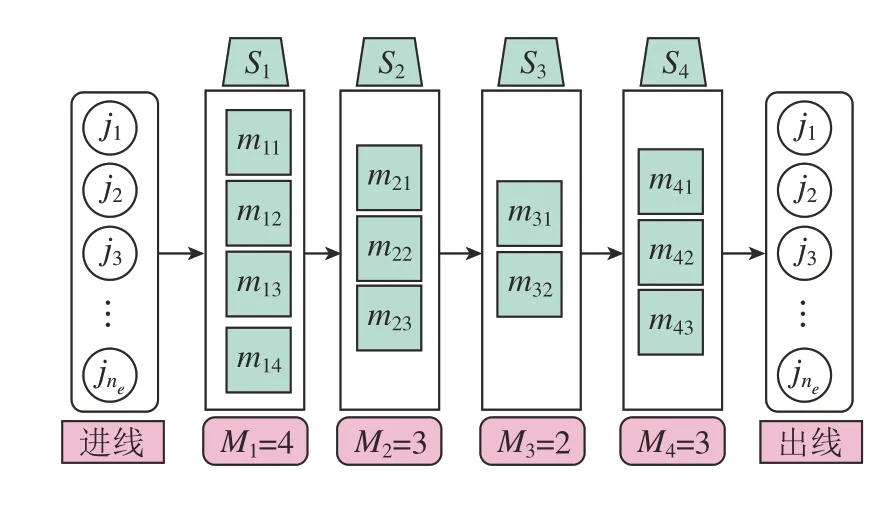
图1 混合流水车间物料流动示意图Fig.1 Diagram of material flow in hybrid flow shop

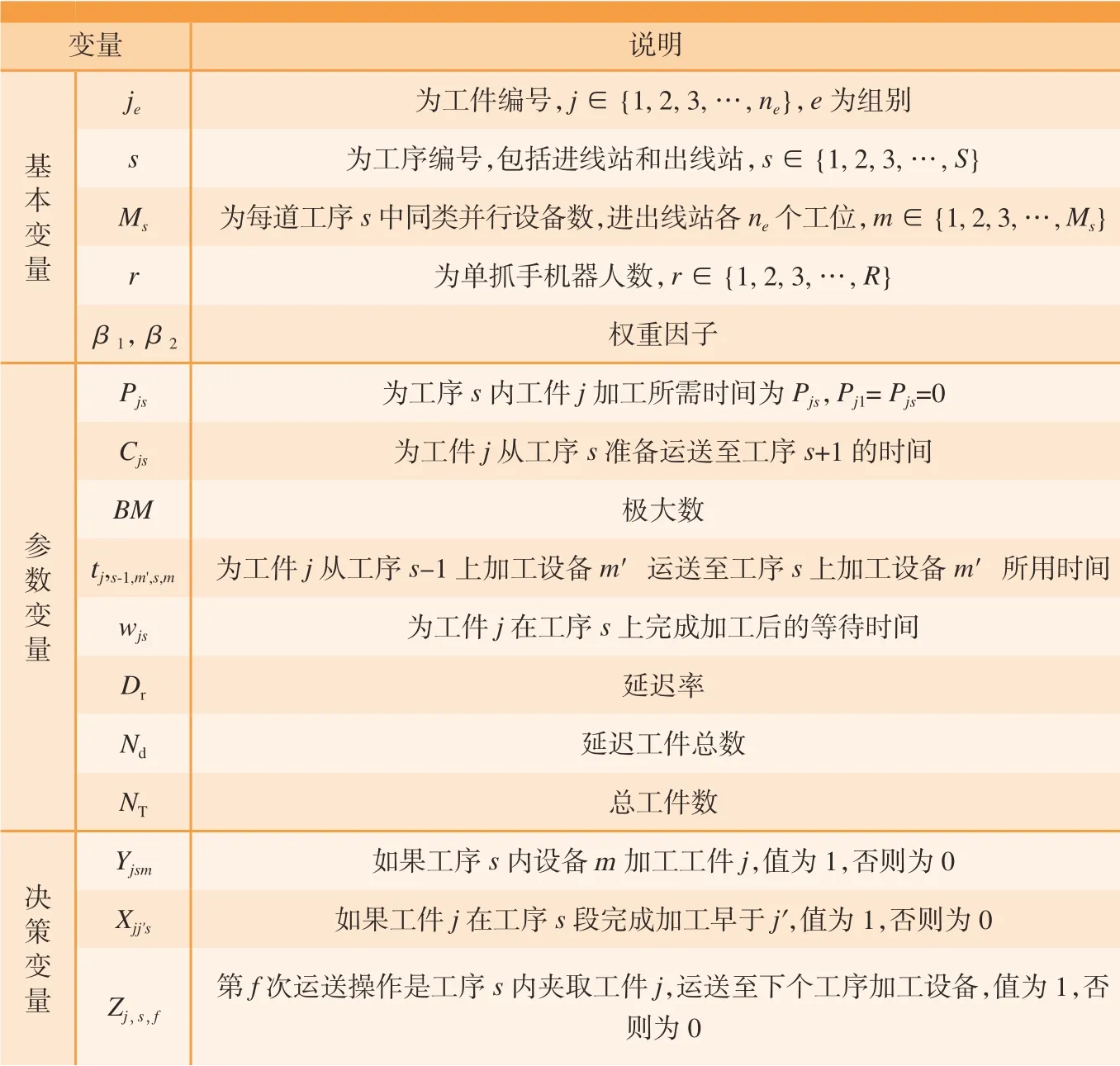
表1 符号说明Table 1 Problem notation

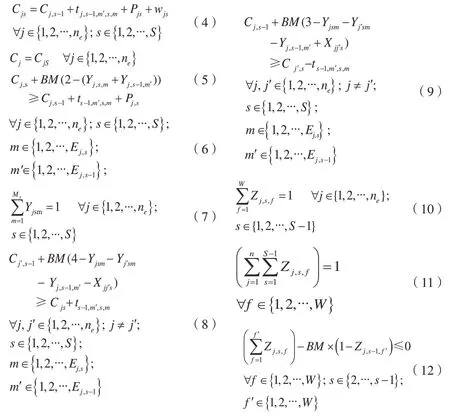
上述模型中：式（1）最小化最大完工时间；式（2）最小化延迟率；式（3）最小化综合优化目标；式（4）每个工件各阶段完工时间；式（5）各工件的完工时间；式（6）用来约束工件按照工序加工；式（7）工件在各工序段中只能在一个加工设备上完成加工；式（8）和式（9）用来约束在每个工序中同一设备工件的加工顺序；式（10）和式（11）确保每个机器人在任何时候只能运送一个工件；式（12）确保每个工件运送过程按照工序的先后顺序进行；式（13）和式（14）机器人的调度顺序符合工件在同一设备的处理顺序。

马尔科夫决策模型建立

文中将多机器人调度过程转化为马尔科夫决策过程[20-21]，通过四元组描述为（S,A,P,R）。其中S为调度车间状态空间，车间现场状态s∈S；A表示动作空间，由调度规则、工序ID、机器人ID组成；P（s,A,s'）= 1，一旦动作选择，状态从s转换至s'的概率为1；R表示在状态s下执行动作a状态转换至s'所得报酬。如图2所示，根据混流车间的调度问题数学约束关系建立物料车间环境，马尔科夫决策过程即为智能系统根据当前车间环境选择一个机器人运送动作a作用于车间，完成运送后车间状态发生改变，同时产生一个奖励信号反馈给智能系统。智能体再根据奖励函数和车间状态s选择下一个动作a'。针对多机器人混流车间调度的实际情况，将车间运行中的状态、动作和报酬函数定义如下。

1 状态

将车间设备特征信息与任务信息组成一个状态变量来引导调度决策，即在时间t时状态向量St=（Tt,Ft,Rt），Tt代表待运送工件特征信息，Ft代表车间状态信息，Rt代表机器人特征信息。

（1）Tt为3×s矩阵，Tt（:,1）至Tt（:,s）依次为进线工位至最后一道加工工序的统计信息。Tt（1,:）为每道工序中待运送工件数目，Tt（2,:）代表每道工序待运送工件平均剩余时间，Tt（3,:）代表每道工序待运送工件中最小剩余时间。

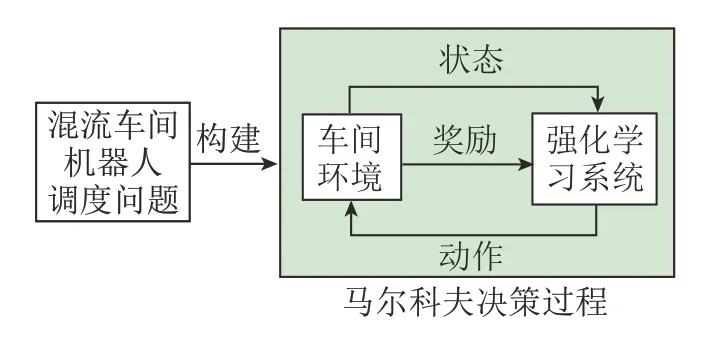
图2 车间调度的马尔科夫决策过程Fig.2 Diagram of Markov decision process for flow shop scheduling

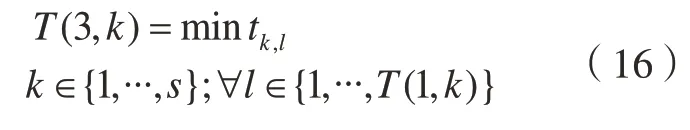
式中tk,l代表在第k阶段待运送工件l的剩余时间，该参数反映工件的紧迫程度。

（2）Ft为车间现场状态描述矩阵，Ft为3×s矩阵，Ft（1,:）表示每道工序的空闲设备数，例如Ft（1,1）=1 即为工序1中有1台空闲设备。Ft（2,:）为每道工序中正在加工状态的设备数，Ft（3,:）代表每道工序中被待运送工件占用的设备数。

（3）Rt为2×i矩阵，表示各机器人的工作状态。i与机器人ID对应，Rt（1,:）表示机器人的状态，Rt（1,2）=1为2号机器人“运送”，Rt（1,2）=0为“空闲”。Rt（2,:）为机器人当前位置ID。

2 动作

动作即为机器人的运送行为，其通过工序ID，调度规则和机器人ID组成向量at=（Sat,Rut,Rbt）。工序ID选择调度工件所在工序，调度规则选择运送工件，同时，机器人ID确定哪一台机器人被选中用于调度。文中选用5种调度规则用于缓冲工位调度，SSO用于工序内待运送工件调度。调度规则的详细描述如表2所示，Sat={进线缓冲工位=0,工序=1,…,s},Rut={SPT=1,LPT=2,SLACK =3,SPT/TWK=4,LPT/TWK=5,SSO=6},Rbt={1=robot 1,2=robot 2,…,r=robotr}，通过上述动作设计，时间t时将在指定规则下分配机器人运送指定工序下的唯一任务。

3 奖励函数

奖励函数被用来对当前行为和调度策略进行评估，由于SP–MCTS是通过最终收益回溯逐个更新节点信息，而本文将最小化最大完工时间和延迟率作为综合评价指标，因此奖励函数设计为：

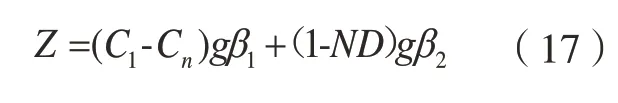
式(17)中C1为子树内第1次搜索至当前所有工件完成加工时所得时间，Cn为子树内实时状态节点的第n次搜索所得时间，其中项C1–Cn若大于0则取实际差值，若小于0则取0值。ND表示当前子树延迟率(延迟工件包括当前搜索中出线延迟的工件和线内剩余时间小于0的工件，总数即为子树中的所有工件)，b1，b2为权重因子。

方法论述

1 多层子树设计

SP–MCTS是一类利用模拟运行过程来评价非终端状态的搜索树算法。模拟过程中选择执行动作，直到达到一个终端状态，并基于多次模拟中平均奖励，以此评估每个动作的潜力[22]。针对工业物联网下混流车间多机器人调度问题提出基于SP–MCTS算法的多层子树自适应优化方法，如图3所示。图3中根据各组任务和当前车间环境依次建立多个子树（TR1,TR2,…TRn）进行策略优化，如子树TR1进行实时优化时，是以车间当前状态作为根节点，组内所有工件完成加工作为目标状态，应用SP–MCTS算法进行优化，并取使节点收益最大的分支规则作为运送动作。根据实时状态依次进行优化，最终取最优路径节点S43（组间临界实时状态，即进线工位清空，工件全部进线加工时）作为下一个子树TR2的根节点原始环境，此时下一组进入缓冲区的工件与当前车间环境建立子树TR2根节点，从而依次优化直至各组工件完成加工。

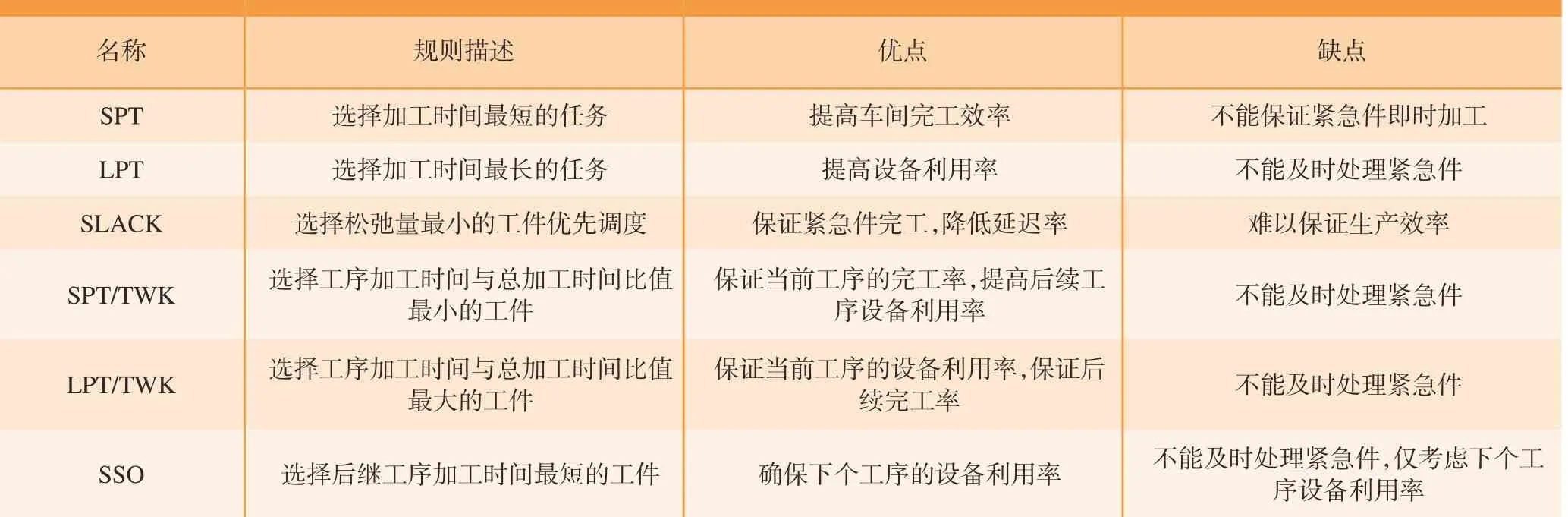
表2 调度规则Table 2 Scheduling rules

如图4子树模拟优化过程，工序内和进线出线缓冲区的数字“1,2,3”分别代表工件等待、加工、和出线3种状态，各工序的平行设备数为“2 2 1 2”。在子树TR1内，若实时车间为状态s1，优化完成后执行策略π（s）至s2，然后保留节点s2下的子树信息，丢弃其他节点信息。此时等待下一个实时调度状态信息与s2进行对比，若相同则以根节点s2继续优化（子树节点信息可累积使用）。依次搜索和节点更新，最终直至该组调度完成。

2 基于SP-MCTS强化学习

结合SP–MCTS算法寻优特性，设计适应于文中混流车间调度问题的选择、扩展、模拟和回溯方案[23]，如图5所示。

2.1 选择

选择步骤始于当前根节点s0，终止于树中叶节点sL，其选择策略根据UCT[24]（Upper confidence bounds applied to trees）算法构建，其改进如下：

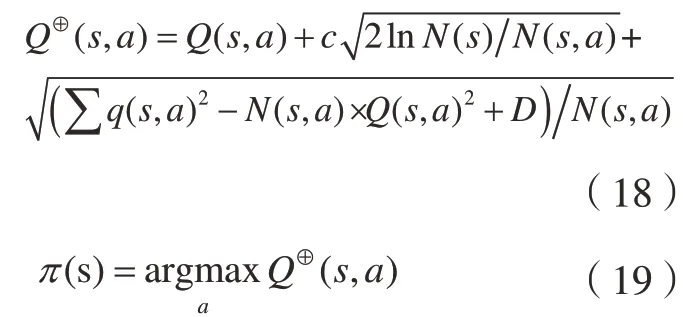
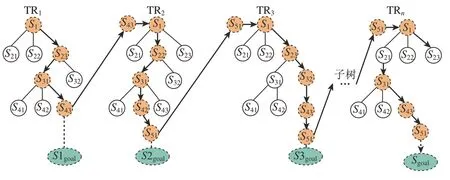
图3 基于SP-MCTS算法的多层子树示意图Fig.3 Diagram of multi-layer subtree based on SP-MCTS algorithm

式（18）中N（s）代表状态s被访问的次数，N（s,a）表示状态s时执行运送动作a的次数，Q（s,a）表示节点s处选择运送动作a的平均收益，∑q（s,a）2表示到目前为止在状态s处执行动作a获得收益Q（s,a）的平方和。式（19）中π（s）代表状态s下的最优策略。

2.2 扩展与模拟

如果搜索至叶节点sL且该节点遍历次数大于P（P为节点扩展临界值）时，应用选择策略后执行动作a得到状态sCL。此时将状态sCL扩展为树中叶节点且节点信息初始为{N(sL,a)=0,Q(sL,a) = 0,N(sCL)=0}。

图4 子树优化过程Fig.4 Subtree optimization process

如果搜索至叶节点sL且该节点遍历次数小于P时，sL将作为初始的模拟节点。在模拟过程中，每一次执行模拟策略前需对线内工件评估紧迫度，若剩余时间tkr<2Tr（tkr任务k的剩余时间，Tr为车间中设备最大距离间机器人运送时间)，则执行LLF作为模拟策略，否则执行既定的3种模拟策略SPT，LPT和随机策略(Random)。

2.3 回溯

当模拟至终止状态时，信息更新从模拟的初始叶节点sL回溯至根节点s0。更新各遍历节点信息：

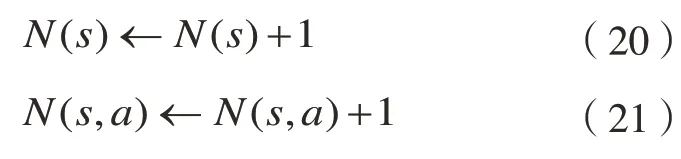
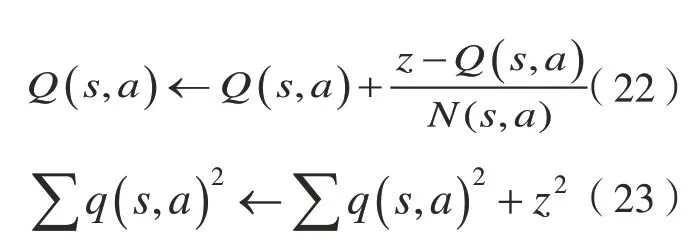
式（20）更新节点s被访问的总次数。式（21）记录s状态下动作a被执行的次数，式（22）更新节点s执行动作a的平均收益。式（23）计算收益求平方和。

3 系统架构

如上所述，文中提出了基于SP–MCTS求解工业物联网的混流车间多机器人调度问题，其体系架构如图6所示。

该架构包含4个子模块，基于工业物联网的混流车间，系统状态模块，SP–MCTS模块和规则与执行动作模块。在机器人完成运送或空闲时且有新工件组进入缓冲区或状态改变时，调度过程立即触发。此时，工业物联网采集混流车间内各制造资源实时状态，并且发送实时信息至系统状态模块以提取关键状态信息，这些信息包括任务信息和设备信息。上述这些关键信息最终被传输至SP–MCTS模块用于优化调度策略。数据经SP–MCTS模块处理后，输出数据至规则与执行动作模块。最终，规则与执行动作模块根据规则选择调度工件并规划机器人传输动作，从而实现基于工业物联网混流车间自适应调度的闭环反馈机制。

4 基于SP-MCTS系统优化过程

SP–MCTS系统自适应优化过程可分为扩展方法和剪支方法。如图4所示，以实时状态s1为根节点，多次迭代后建立了TR1，满足停止条件时，则依据策略π(s)执行动作a得到实时调度状态s2，此时以s2为根节点继续搜索，实时状态依次建树的过程称为扩展过程。选择动作a时，树内则保留节点s2以下分支，剪掉其他分支即剪支过程，这样依次搜索直至目标状态sgoal。其求解混流车间多机器人调度问题的流程图如图7所示，SP–MCTS算法伪代码如算法1所示（表3）。

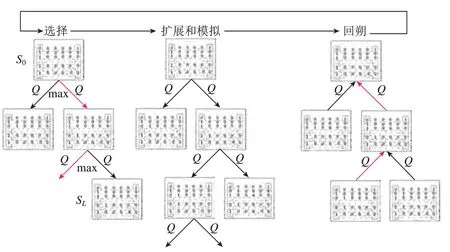
图5 SP-MCTS算法原理图Fig.5 Schematic diagram of SP-MCTS algorithm

图6 应用SP-MCTS的多机器人调度方法架构Fig.6 Architecture of multi-robot scheduling approach using SP-MCTS

方法验证与讨论

为评估所提方法的有效性，在此提出基于工业物联网混流车间多机器调度的案例用于模拟验证。

1 案例描述

应用西门子Tecnomatix 数字化平台作为案例模拟软件，如图8所示，混流车间主要由9台加工设备以及4道工序组成，其中9台加工设备、进线缓冲工位、出线缓冲工位均匀分布于机器人轨道两侧，且有两台机器人用于物料运送。

2 应用SP-MCTS进行多机器人调度

应用TensorFlow软件和西门子Tecnomatix 数字化平台联合模拟工业物联网下混流车间多机器人实时调度系统，如图9所示。

该系统软件可分为两部分，分别是在TensorFlow平台使用python开发的SP–MCTS程序和使用西门子Tecnomatix平台模拟软件开发的模拟程序。其整个模拟程序分为以下几个子模块：设备管理、任务管理、状态管理、通信模块和调度指令模块。在模拟车间生产过程中，设备管理模块负责车间内加工设备、机器人和各类传感器的信息管理；任务管理模块负责所有工件的管理；状态处理模块作为关键的信息处理模块，其作用是处理从设备管理和任务管理模块发送的实时设备和工件信息，并将提取的关键信息发送至通信模块。通信模块是在SP–MCTS程序和模拟程序间建立一个通信网络，实时传输状态信息和调度指令信息。SP–MCTS优化策略根据当前状态优化调度策略，将调度策略发送至调度指令模块。最后，调度指令模块根据策略协调规则和机器人执行调度任务。

3 案例描述

混流车间内的设备、任务、机器人以及计算机模拟环境等参数设置如下：

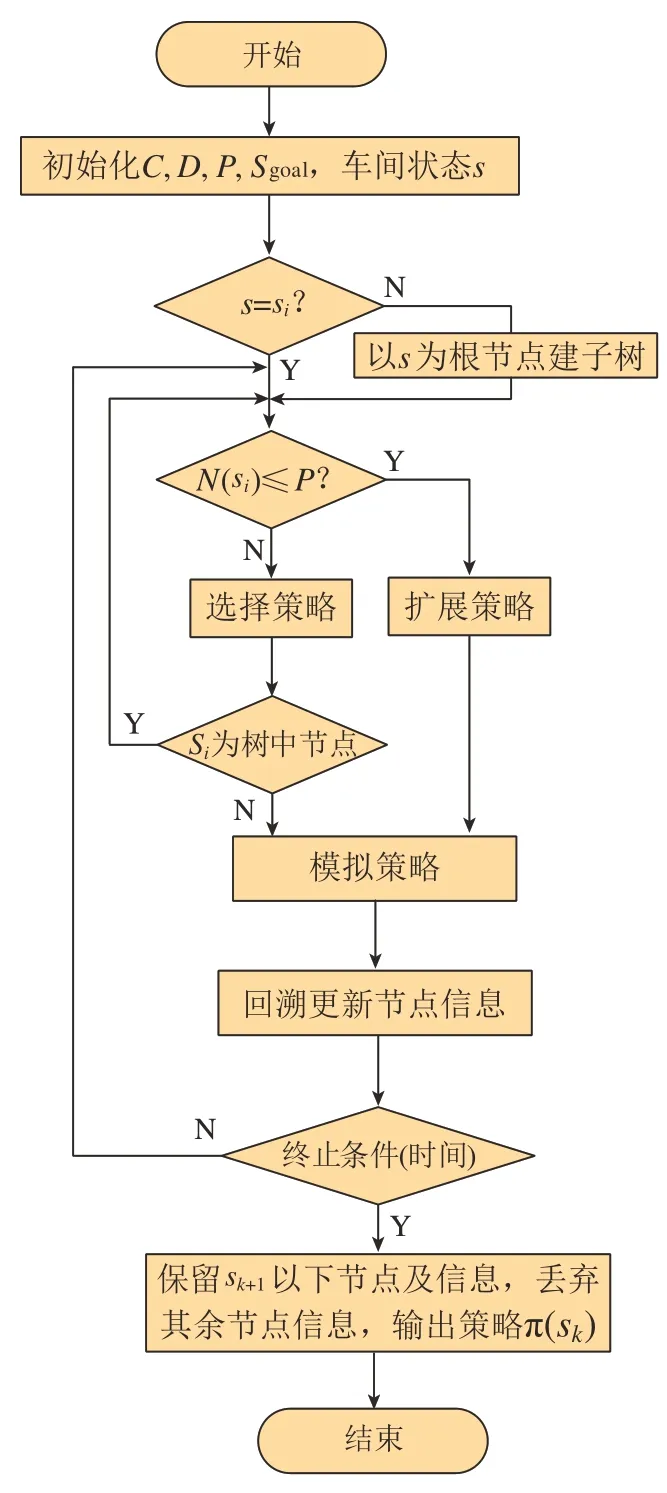
图7 混流车间多机器人自适应调度流程Fig.7 Multi-robot scheduling process with SP-MCTS

（1）总的加工任务数为500,进线缓冲工位有20个工位，根据紧迫度确定工件的进线次序，如果存在紧迫度相同的产品，则按交货期由早到晚排序[23]。从而将500个任务分成25组，依次送入进线缓冲工位。

（2）工件在每个工序的加工时间服从(10,50)的均匀分布。

（3）为使问题简单化，文中在机器人运输过程中不考虑最优路径和机器人碰撞冲突问题，同时工件运输时间服从(0.5,1)均匀分布。

（4）参数(C,D)设置为(0.5,10000)[25]，P=3，b1=0.5，b2=2。

（5）计算机模拟环境为i7–6700 CPU@3.40GHz,16G RAM。

依据上述参数取一组车间加工参数，应用SP–MCTS算法对模拟车间中物料进行实时调度。如图10所示，以第一组进线任务的路径节点与最大收益值为例，可以看出在前期搜索中随着节点经验信息依次累加，收益数值快速提高，后期搜索中随着状态空间不断缩小，树节点越深其收益数值变化越趋平缓，且数据波动越趋收窄。因而说明应用SP–MCTS在实时优化中能够快速准确地选择最优策略进行物料调度。

表3 算法1: 基于SP-MCTS算法的优化主程序Table 3 Algorithm 1：Optimized main procedure based on SP-MCTS

图8 混流车间多机器人调度模拟环境Fig.8 Simulation of multi-robot scheduling on shop floor environment

图9 混流车间多机器人调度系统Fig.9 Implementation of the SP-MCTS based multi-robot scheduling system

4 结果分析

在此引入RLVNS[18]、AHP[15]、SPT、LPT和SLACK与本文所提方法进行对比，在相同的环境下处理随机生成的500个任务，通过完工时间和延迟率进行综合比较。

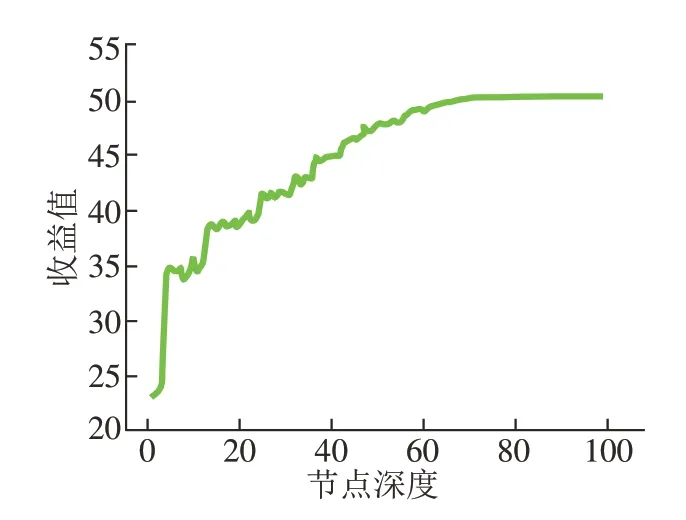
图10 子树内节点深度与收益值关系Fig.10 Relationship between node depth and revenue value in subtree

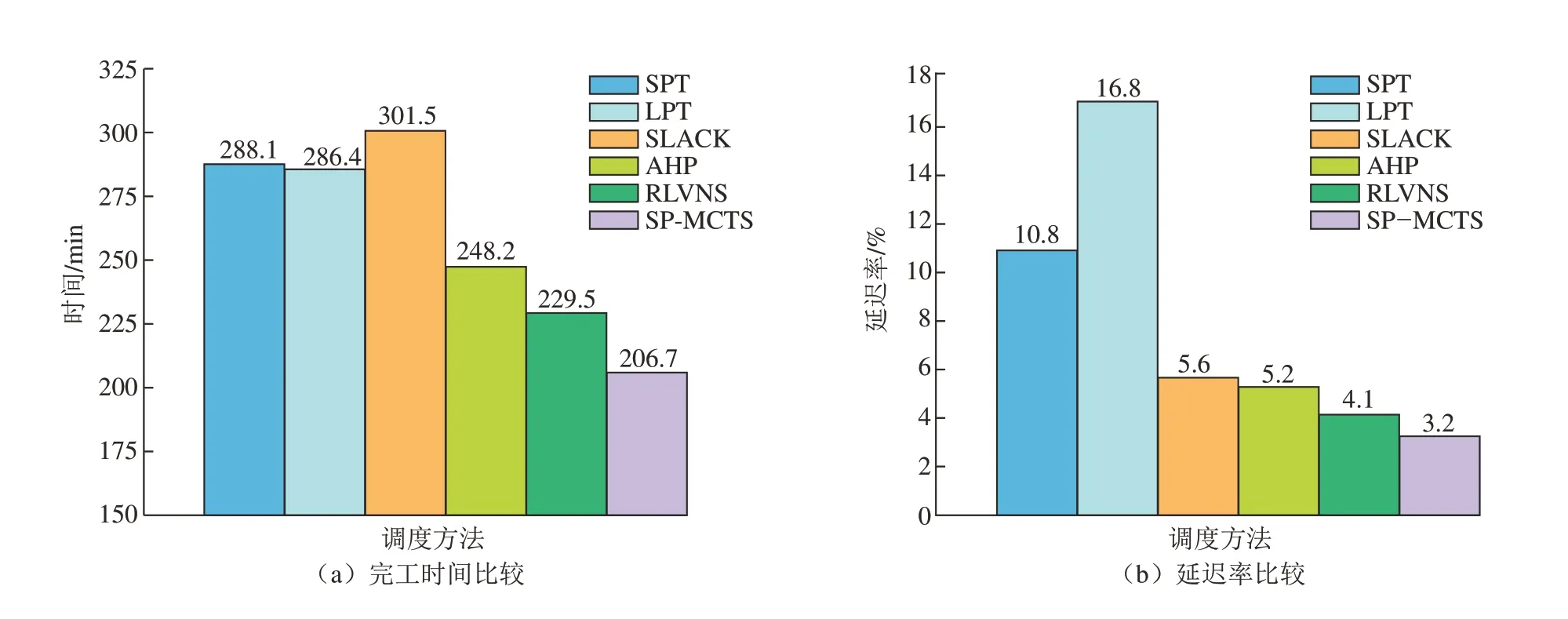
图11 各方法比较结果示意图Fig.11 Diagram of comparison results of scheduling methods

随机产生10组案例车间参数应用各方法分别优化，然后取平均值进行比较，如图9所示。多机器人调度方法比较示意图见图11，可以直观看出5种方法在完工时间和延迟率两个指标下的比较结果。与SPT、LPT和SLACK规则相比，SP–MCTS算法调度所得完工时间分别降低了28.3%、27.8%和31.4%，同时延迟率分别降低了70.4%、81%和42.9%；而相比于AHP和RLVNS方法，完工时间分别降低了16.7%和9.9%，延迟率分别降低了38.5%和22%。由此看出，单一的SPT、LPT和SLACK规则调度，虽然能快速响应，但其适应性差且调度质量难以保证，而应用SP–MCTS算法搜索寻优后建立信息网络，其结合现场状况在多种规则中选择适应当前状态的最优调度策略，从而得到更好的求解质量。

基于SP–MCTS解的质量优于多规则组合AHP方法和强化学习RLVNS方法，可知，与多规则组合AHP方法相比，SP–MCTS算法的适应性更强；而RLVNS方法只考虑第一工序的邻域搜索学习，不能够分辨工序之间工件调度时的信息差异，存在明显的局限性。因此，该模拟结果验证了在工业物联网下应用SP–MCTS对混流车间进行多机器人调度的有效性和优越性。

结论

为最小化工业物联网混流车间中多机器人调度的完工时间和延迟率，本文提出基于SP–MCTS算法的自适应调度方法。由于工件分组进入缓冲工位，因而采用分层子树搜索机制，应用SP–MCTS以实时状态为节点进行搜索和信息积累，然后根据现场情况快速选择合适的规则和物料机器人，从而达到了自适应调度目的。主要结论如下：

（1）分层子树优化，使得各组工件从一个完整的根节点出发同时兼顾相邻子树，简化了模型难度。

（2）状态依次作为根节点搜索，能够根据累积的节点信息，精确快速定位动作分支，提高了搜索效率。

（3）在模拟实验中与AHP方法和调度规则比较，验证了SP–MCTS方法的适应性；同时SP–MCT求解的完工时间和延迟率均优于RLVNS方法，验证了SP–MCTS方法在求解混流车间调度问题时的搜索理念的优越性。

本文调度方法架构简明，易于实现，为进一步解决工业物联网下车间实时调度问题提供了参考。下一步，将结合深度学习方法建立各规则的概率网络和价值网络，从而使调度系统成为一种有意识的智慧大脑。