基于遗传算法的机器人负载重力补偿优化算法研究*

李 根，李鹏程，吴 超，沈 烨

（南京航空航天大学机电学院，南京 210016）

随着新型航空装配对装配精度以及研制周期的要求越来越高，工业机器人应用在航天装备自动化装配的场合越来越多[1–2]。在利用机器人进行装配任务时，有很多场合是机器人与人在共享的工作空间中协作完成复杂的任务，即人机协作，而外力感知是实现人机协作的关键技术之一[3]。

在现阶段，对于机器人装配，通常是在负载与工业机器人末端法兰之间安装六维力传感器（下文简称为力传感器），以实现机器人的力反馈控制。力传感器的主要功能是感知作用在其敏感端的力及力矩并使之三维正交化[4]，机器人在静止状态下时，力传感器的测量数值由3部分组成：负载重力、力传感器零点和施加外力。负载的存在会干扰对外力的感知，对于人机协作而言，从测量数据中得到精准外力信息格外重要，因此需要对安装在力传感器上的负载进行重力补偿。

在机器人末端负载重力补偿方面，Stavros[5]从力传感器测量值的组成出发，通过将机器人末端移动到特定位置来标定力传感器的质心和重量；Kim等[6]提出了在重力补偿之前对六维力传感器进行回零处理，从而消除零点漂移误差；Kubela等[7]提出了利用机器人姿态来计算负载重力作用在六维力传感器各方向的分力，并通过KUKA公司的RSI通讯进行了实时负载重力补偿；张光辉等[8]在机器人运动学的基础上，将力传感器信息和负载信息转换至基坐标系求解；缪新等[9]将力传感器坐标系和法兰坐标系分开考虑，通过最优解的方式，利用多组机器人姿态测量数据，计算出力传感器偏角；高强等[10]先在机器人原点测量负载重力，然后在机器人运动时，利用基坐标与力传感器的旋转矩阵，将负载重力转换至力传感器坐标系进行求解，从而抵消负载重力；张立建等[11]通过最小二乘法，利用不少于3个随机机器人姿态的力传感器数值，分别计算出传感器零点、负载重力重心、机器人安装倾角。

其中，文献[5–10]都是假设世界坐标系与机器人基坐标系重合，即重力方向为机器人的Z轴，但在实际情况下，例如安装在AGV上的机器人，其基坐标系并不一定与世界坐标系平行。而且，文献[7–10]未考虑力传感器的零点漂移，默认力传感器的初始值为0，这与事实不符。虽然文献[5–6]考虑了零点漂移问题，但它们未考虑在每次安装负载后，力传感器零点都会改变，如果每次都按照文献中的方法进行标定，标定时间过长。文献[11]默认力传感器坐标系与法兰坐标系平行，这对连接件的制造精度有非常高的要求，但如果遇到如文献[9]中力传感器与法兰安装误差角度过大的情况，则会出现很大误差。

综上所述，在现有的关于负载重力补偿的研究中，大多默认机器人基坐标系Z轴与重力方向相同，但在实际情况中，往往需要考虑基坐标系与世界坐标系的关系。在进行补偿时，应该综合考虑力负载重力、传感器零点漂移、机器人安装倾角、力传感器安装偏角。对于航空航天装配系统而言，由于大多都是大负载，为了使机器人得到更加精准的外力感知能力，应该尽可能使补偿效果达到最好。

本文研究一种工业机器人末端负载重力补偿优化方法，通过分析机器人系统各部分之间的位置关系，建立重力补偿模型，考虑力传感器安装偏角对补偿结果的影响，以误差平方和最小为目标建立最优解模型，利用遗传算法进行求解，同时在测量时设置了特定姿态来减少系统误差，最终可以在不使用测量仪器的情况下，估计力传感器安装偏角，从而提高重力补偿精度。

重力补偿计算模型建立

本文的重力补偿模型一部分参考了文献[11]。

1 坐标系关系建立

机器人系统由机器人本体、力传感器、负载组成。设世界坐标系为Ow–XwYwZw，机器人坐标系为Or–XrYrZr，法兰坐标系为Of–XfYfZf，力传感器坐标系为Os–XsYsZs，它们之间关系如图1所示。

假设世界坐标系的Zw方向与重力方向平行且反向。

规定以下转换关系：

（1）Os–XsYsZs相对于Of–XfYfZf的姿态转换矩阵为RZ（γ）。

（2）Of–XfYfZf相对于Or–XrYrZr的姿态转换矩阵为RZ（C）。

（3）Or–XrYrZr相对于Ow–XwYwZw的姿态转换矩阵为RY（ω）。

其中，R为3×3的旋转矩阵。的设置是为了表示机器人安装平面与地面的安装倾角，一般只存在于Ow–XwYwZw的XwZw平面和YwZw平面，因此不考虑Os–XsYsZs相对于Ow–XwYwZw的Zw轴旋转。

2 力传感器与负载关系

首先假设无外力，以力传感器坐标系为基准分解负载重力，如图2所示。

从图2中可以得到：

图1 坐标系关系Fig.1 Coordinate system relationship

图2 力传感器坐标系与负载关系Fig.2 Relationship between force sensor coordinate system and load

将式（2）代入式（1）并整理成矩阵形式可得式（3）。

其中，d1=Tx0+Fy0×z–Fz0×y，d2=Ty0+Fz0×x–Fx0×z，d3=Tz0+Fx0×y–Fy0×x。

可简写为：

通过改变N次不共面的机器人姿态（N≥3），在机器人稳定后，读取力传感器数值，得到N组力传感器测量数据,整理可得：

式（5）两边同时左乘ΦT可得：

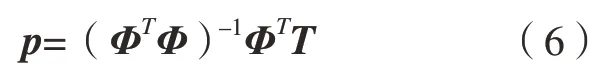
由此可以算出负载在力传感器坐标系下的坐标（x,y,z）以及d1,d2,d3。

3 力传感器与机器人本体关系

重力在世界坐标系Ow–XwYwZw中的方向向量为gw=[0 0–1]T,则重力在力传感器坐标系Os–XsYsZs中可以表示为：

其中，k1=Gcosθsinω,k2=–Gsinθ,k3=–Gcosθcosω。

由式（2）可得：

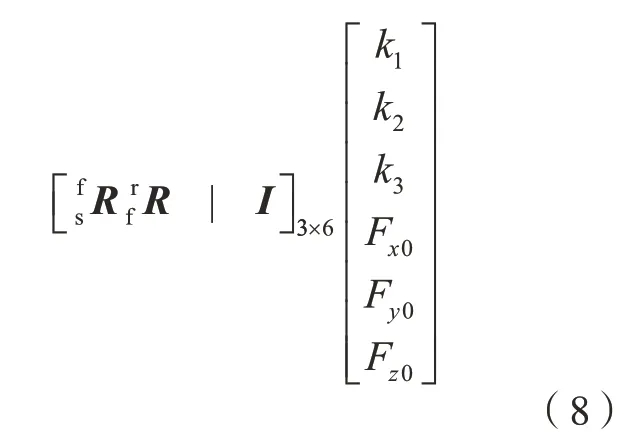
可简写为:

其中，K=[k1k2k3Fx0Fy0Fz0]T。根据前文得到的N组测量数据，整合可得：

式（10）两边同时左乘RT得：

由此可以算出k1、k2、k3、Fx0、Fy0、Fz0。

进而可得

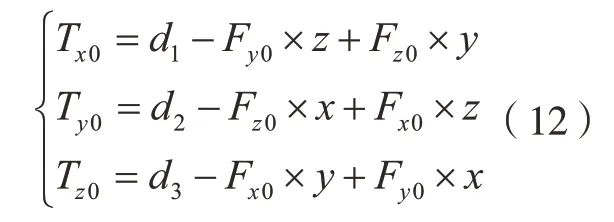
至此，若力传感器安装偏角α、β、γ已知，可将负载在力传感器坐标系下的坐标（x，y，z），力传感器零点[Fx0Fy0Fz0Tx0Ty0Tz0]T，负载重量，机器人底座倾角θ=arcsin（–ky/G），ω=arctan（–kx/kz）全部得出。

4 力传感器与法兰的关系

连接件与法兰、力传感器连接处一般通过定位销定位，用螺栓连接，只要连接件的机械加工精度达到要求，一般认为法兰坐标系Of–XfYfZf和力传感器坐标系Os–XsYsZs平行，即α=β=γ=0。但有时由于加工误差、安装误差等因素，往往会出现或大或小的传感器安装偏角，而这些角度很难测得。因此，为了获取更加准确的传感器安装偏角并使重力补偿效果提升，对重力补偿算法进行了优化。

重力补偿优化算法研究

1 重力补偿误差分析

本文的重力补偿算法是建立在最小二乘法的基础之上的，而最小二乘法的目的是使所求数据与实际数据之间的误差平方和最小[12]，因此误差平方和是判定所求数据是否更贴近于实际的指标。当无外力时，对于第i个（1≤i≤N）测量姿态有

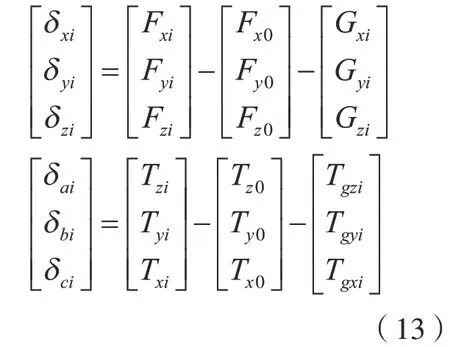
其中，δxi、δyi、δzi、δai、δbi、δci、为第i个测量姿态下的重力补偿误差，Fxi、Fyi、Fzi、Txi、Tyi、Tzi为第i个测量姿态下的实际测量值（即力传感器数值），Gxi、Gyi、Gzi、和Tgxi、Tgyi、Tgzi可分别由式（7）和式（1）得到。从前文的重力补偿模型可以看出，重力补偿误差与负载重量G有密切的关系，而负载重量G与六维力传感器的测量力值相关。因此本文的优化模型只考虑测量力值。

令

其中，S为测量误差的平方和，根据所述算法可以发现，它是一个关于α、β、γ的函数，若α、β、γ已知，误差平方和S便可以求出。

2 优化模型建立

通过仿真发现，α、β、γ越接近实际转角，误差的平方和会越小，且重力补偿效果会越好。因此，可以利用寻找最优解的方法，找出误差的平方和最小时的α、β、γ值，将其设为预测值，步骤如下。

α、β、γ的值由两部分组成，可以表示为：

其中，α0、β0、γ0为传感器偏角的初始预估值，Δα、Δβ、Δγ为传感器偏角的优化值。

如果连接件的加工误差不大，Of–XfYfZf和Os–XsYsZs的XY平面几乎重合，因此β0、γ0一般设置为0°。α0可以通过安装传感器时法兰X正方向与传感器X正方向的关系设置，如果同向，α0可以设置为0°；如果反向，α0可以设置为±180°，以此类推。

给Δα、Δβ、Δγ设置一个范围，即

其中，lα、lβ、lγ分别为Δα、Δβ、Δγ的下界，uα、uβ、uγ分别为Δα、Δβ、Δγ的上界。范围的选取与初始预估值的准确度有关，如果初始预估值较为准确（例如法兰X正方向与传感器X正方向几乎重合），可以选取在一个较小的范围；相反，如果初始预估值无法准确预估（例如传感器与法兰之间随机安装），可以选取一个较大的范围。Δα、Δβ、Δγ的范围影响遗传算法的计算效率及准确度。

那么优化问题可以描述为：

本文采用遗传算法对优化问题进行求解。

由于求解的是目标函数最小值的优化问题，所以应对原始的目标函数进行变换：

其中，Cmax为参考系数，根据试验经验，一般取10左右；0为遗传算法中的个体。

个体编码采用浮点数编码方法。假设lα=lβ=lγ= –1，uα=uβ=uγ=1，由于染色体X的初始值是随机的，则

其中，xα，xβ，xγ∈[–1.000，1.000]，精确到小数点后3位，比如，X的表现型可以是[–0.061，0.123，–0.950]T。

使用乘幂尺度变换的方法进行适应度评价，即

其中，F′表示变换后的适应度，k为调整参数，F是步骤(1)中的变换目标函数。

选择算子采用比例选择方法，变异算子采用均匀变异的方法，交叉算子选择每个基因的相连处。群体大小M、交叉概率pc（0.4～0.99)、变异概率pm（0.0001～0.1）、终止代数T（100～1000）根据Δα、Δβ、Δγ的取值范围具体调整，其中群体大小M可以选取较大的数。由于篇幅原因，在此不进行具体描述。

通过遗传算法算出最优解，设选取的值为Δαc、Δβc、Δγc（用下标c表示其已知），使α=α0+Δαc，β=β0+Δβc，γ=γ0+Δγc，得到预估的传感器安装偏角。

试验验证

1 试验条件

试验采用KUKA公司的KR210–2700机器人，其主要参数见表1。六维力传感器采用ATI公司的Gamma IP60型传感器，其测量范围及精度参数见表2。

试验用的力传感器负载重约12kg，试验实物如图3所示。

2 试验过程及结果

图3 重力补偿试验平台Fig.3 Gravity compensation experiment platform

表1 KR210–2700机器人技术参数Table 1 KR210–2700 robot technical parameters

表2 Gamma IP60 F/T力传感器技术参数Table 2 Gamma IP60 F/T force sensor technical parameters

表3 机器人测量姿态Table 3 Robot measuring attitude

由于最小二乘法对于个体数据的误差比较敏感，理论上是测量数据越多，优化结果越好，而获取过多的测量数据会花费较多的时间。因此为了提高优化效果，并避免测量时间冗长，选取对称机器人姿态作为测量姿态，如表3所示。这样设置的好处在于，不仅可以充分利用到每个轴的数据，还可以避免一些不必要的误差。例如，由于传感器的分辨率，当在测量姿态1状态下时，可能Z轴测得的负载重量会多一个或少一个分辨率单位的误差，这就会导致计算结果偏大或者是偏小；而在测量姿态14状态下，Z轴测得的数据会反方向多一个或少一个分辨率单位的误差，根据最小二乘法原理，可使计算结果更加准确。

因为本文的重点在于验证预估力传感器安装偏角的有效性，对于不同负载的重力补偿效果在此不进行赘述。考虑两种情况：

（1）力传感器安装失误（力传感器X正方向与法兰X正方向反向）；

（2）力传感器安装正确（力传感器X正方向与法兰X正方向几乎重合）。

为了更好说明本文方法的有效性，两种情况均不使用定位销，从而使传感器安装偏角存在随机性。下文简称这两种情况为情况（1）和情况（2）。

分别进行试验，每次试验依次调整机器人到表3所列的14个姿态，每个姿态下，连续采集1000组传感器数据，求其平均值作为计算参考数据，表4和表5为试验数据。

在情况（1）时，设置传感器安装偏角初始预估值为[180°，0°，0°]；在情况（2）时，设置传感器安装偏角初始预估值为[0°，°0，°0]。首先分别通过优化前的重力补偿算法得到安装后的负载重力、负载重心、传感器零点、机器人安装偏角。之后利用遗传算法，求解最优解，并将最优解代入算法算出补偿后的重力补偿数据，得到优化前后的数据，如表6所示。

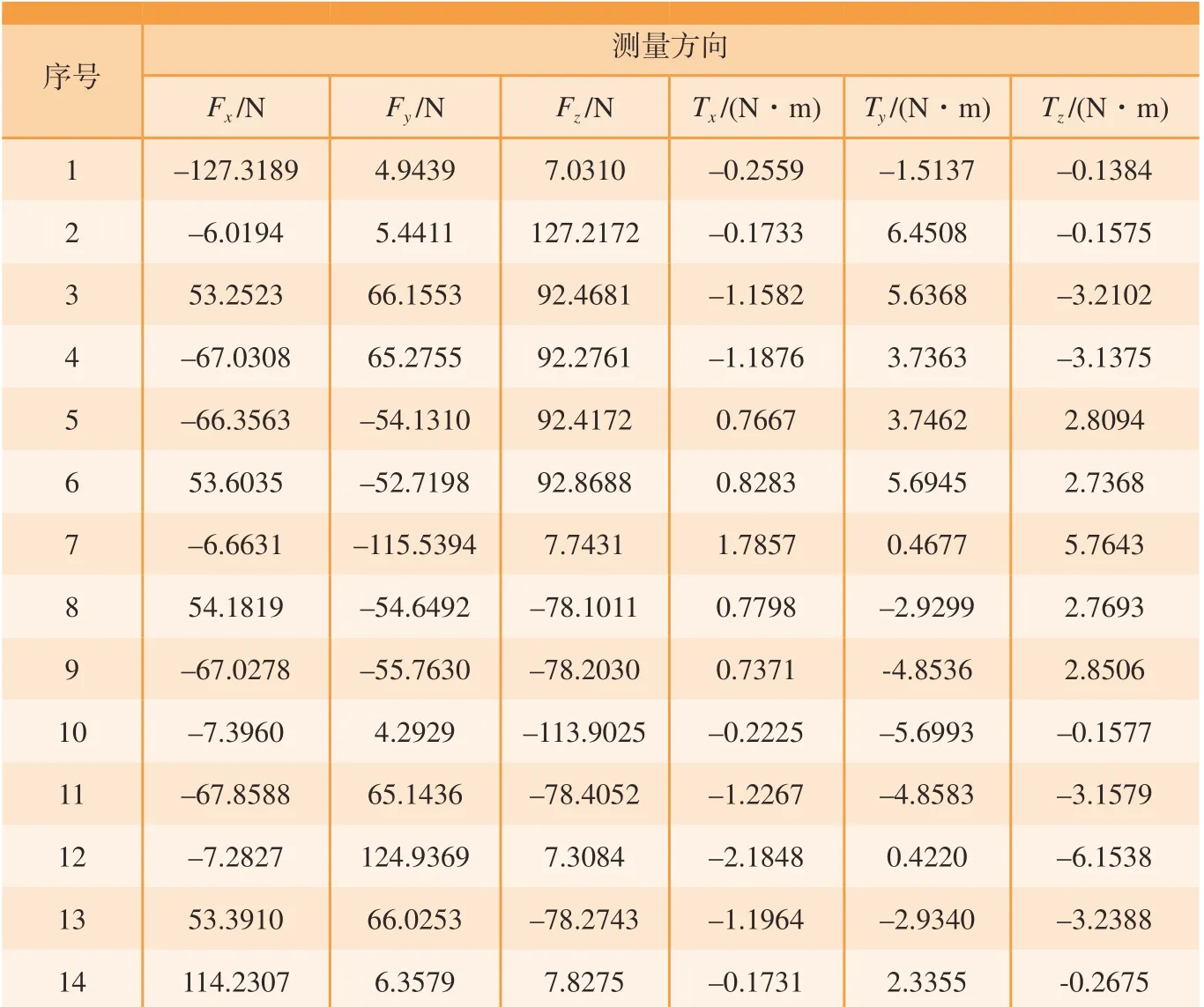
表4 安装失误时力传感器测量数据Table 4 Force sensor measurement data when installed incorrectly

可以看出，无论力传感器安装是否正确，本文的优化算法都可以进行有效预估传感器安装偏角。其中，在情况（1）时，如果不考虑传感器安装偏角，重力补偿结果异常，误差平方和也非常大，而经过优化后，重力补偿结果正常（主要从负载重量项看出），误差平方和大幅度减小。

随后在情况（2）下，任意调整机器人姿态并采集传感器数据，验证姿态如表7所示的，比较补偿传感器安装偏角前后的重力补偿误差，如图4和图5所示。

从图4可以看出，在补偿传感器安装偏角后，各方向的最大重力补偿误差、平均重力补偿误差都明显减小。图5中的合力误差为，合力矩误差为，从中可以看出，与优化前相比，优化后的合力最大重力补偿误差降低（1–0.9095/1.5298）=40.55%，合力平均重力补偿误差降低（1–0.4027/0.7063）=42.98%，合力矩最大重力补偿误差降低（1–0.2602/0.2751）=5.42%，合力矩平均重力补偿误差降低（1–0.2353/0.2507）=6.14%。因此，证明补偿的传感器安装偏角有效。

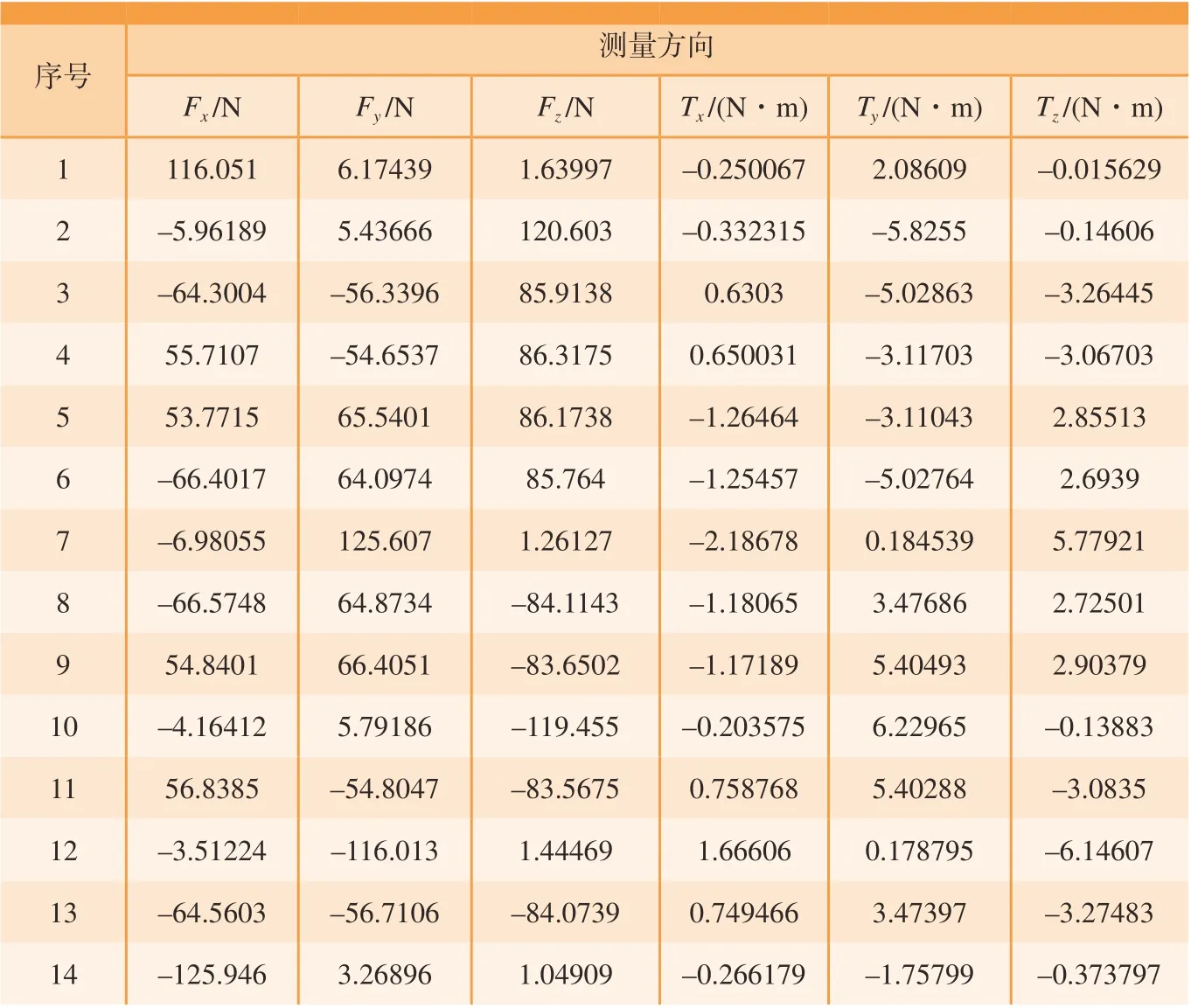
表5 安装正确时力传感器测量数据Table 5 Force sensor measurement data when installed correctly

之后，对负载重力进行测量。根据表5的结果，优化前的负载重力测量值为120.5394N。优化后和负载重力测量值为120.5392N。将负载拆下，和连接用的螺栓一起利用标准仪器称重，测得12.057kg，重量为12.057×9.805=118.218885N。由于力传感器敏感端也有重量，它也被计算在负载重力之内，所以在没有负载的时候，再次移动到表5所示的姿态并测量，对得到的力传感器数值进行求解，得敏感端重量为1.6515N，则测量负载共119.870385N，测量误差在0.558%之内，证明重力补偿结果有效。

如文献[11]所述，姿态误差和采样数据随机误差会影响重力补偿结果，这不仅会影响负载重量的计算，也会进一步导致有些位姿下的优化效果不佳，这就解释了图4和图5中为何会出现优化后误差不降反增的情况，但从总体看来，优化效果良好。

结论

本文面向工业机器人在柔顺控制、人机协作等应用中的外力感知需求，在已有的重力补偿算法上进行了优化。

此方法在最小二乘法的基础上，通过分析力传感器偏角对补偿结果的影响，以误差平方和最小为目标建立最优解模型，利用遗传算法，补偿力传感器安装偏角。试验中通过采集指定姿态下的力传感器数值来减少系统误差，利用遗传算法优化后，任意调整机器人姿态，验证优化效果。试验结果表明，优化后的各方向最大重力补偿误差、平均重力补偿误差均有所减少。

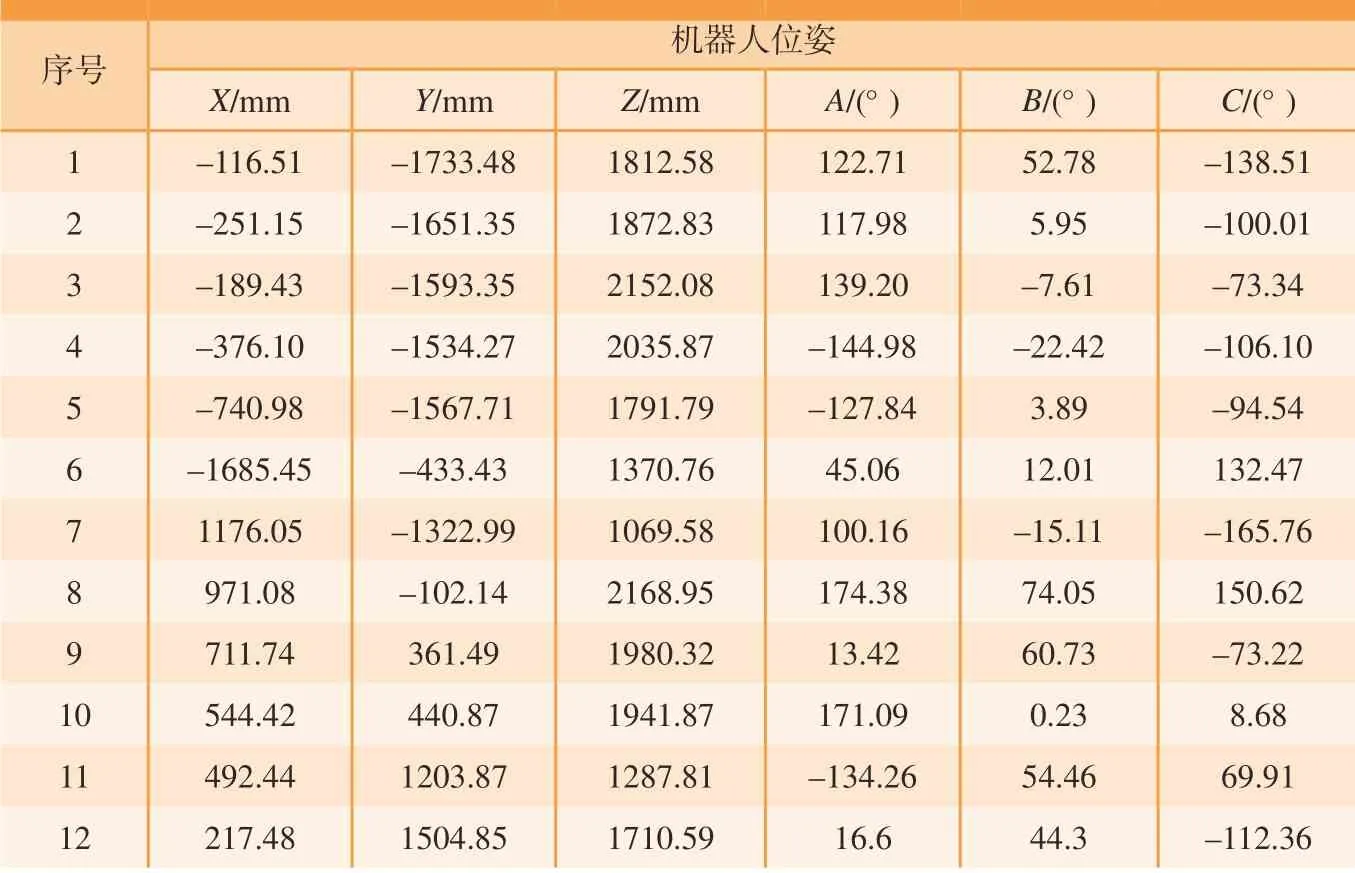
表7 机器人验证姿态Table 7 Robot verification posture

与现有方法相比，本文方法的优势在于可以在不使用外部测量仪器的情况下，估计出力传感器安装偏角。此方法可以补偿由于连接件加工精度不足或者安装失误导致的误差。而已有方法是通过精密的机械结构保证力传感器坐标系与法兰坐标系平行，或者是通过单独调姿过程对力传感器安装偏角、力传感器零点进行标定，这样会增加成本或者增加标定时间。利用本文方法不仅会使效率高、成本降低而且鲁棒性得到提升。

图4 优化前后各方向重力补偿误差Fig.4 Gravity compensation error of all direction before and after optimization

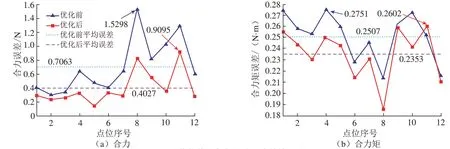
图5 优化前后合力 （矩）重力补偿误差Fig.5 Gravity compensation error of resultant force (torque) before and after optimization