一种基于星型正交幅度调制的SCMA 码本的优化

曾慧，李旭东

（西华大学理学院，成都610039）

0 引言

随着无线通信技术的飞速发展，无处不在的移动服务出现了爆炸式的增长，由于传统的正交多址接入（OMA）已经不能满足海量用户接入的需求[1]，为了满足巨大的流量增长，实现移动无线通信系统在性能和规模上跨越式发展，一种新型的非正交多址接入技术（NOMA）被提出[2]，稀疏码分多址（SCMA）是一种基于码域的新型非正交多址接入技术，其将调制与稀疏扩频结合在一起，成倍提高接入的用户数，有效提高了系统的频谱效率[3]。在SCMA 上行链路研究文献[4]中，在提出非正交多址系统能量分析的框架的基础上，分析了上行链路SCMA 的能量效率，当SCMA 和进阶长期演进（Long Term Evolution- Advanced，LTE-A）系统接入的用户数目相等时，由于LTE-A 系统是正交传输机制，所以平均下来，总体能量效率较高，而SCMA 可以支持接入更多的用户数量，并通过发射端功率控制来提高能量效率。另外，在SCMA 下行链路研究文献[5]中，提出了一种多用户多输入多输出（Multi-User Multi⁃ple Input Multiple Output，MU-MIMO）技术，是为了提高下行系统的容量，并分析了用户配对、功率分配、速率调整及相应的调度算法，表明当SCMA 与多用户多输入多输出技术结合[6]时，可以获得更高的下行系统吞吐量增益，这与4G 长期演进（Long Term Evolution，LTE）相比，采用SCMA 技术可以使下行系统的传输速率和用户的传输速率分别得到提升。SCMA 技术通过多用户接入与开环协作多点（Coordinated Multi-Point，Co MP）结合，为功率域和码域的接入用户的传输提供了优势，使数据流更具有鲁棒性[7]，可以整体性地提高平均小区吞吐量，降低获取信道状态信息，由此，SCMA码本的设计设计尤为重要。

目前，关于SCMA 码本设计仍然是一个复杂且具有挑战性的问题，研究内容的主要思路是根据最大化最小欧氏距离与不同的酉旋转来设计高维母星座图[8]，然后通过映射矩阵和星座矩阵运算得到不同用户的码本。在此基础上，文献[9]提出了一种基于正交振幅调制（Quadrature Amplitude Modulation，QAM）星座的SC⁃MA 码本设计方法，该码本设计的母码本基于星形QAM 星座，与其他用户码本的获得方式大体相同，与现有的码本和低密度签名（Low Density Signature，LDS）相比，基于正交振幅调制星座的SCMA 码本的设计方法在不增加检测复杂度的前提下，可以大幅度提高误比特率性能。设计的大体思路首先是通过一个二维格栅子集来获得母星座的第一维度，第二维度由第一维度的旋转来获得，再通格林映射一对一地将母星座点映射成母码本的码字，最后，对码字的偶数维度进行交织操作生成码本，该码本具有较低的峰均功率比，并且能够对信道衰落具有更好地抵抗能力。另外，也有文献还给出了一种球形码本设计[10]以及基于容量及互信息提出码本设计[11]方法。但这些码本设计方案有的复杂度高且操作性不强，基于此，本文提出了一种基于星型正交幅度调制的SCMA 码本的优化设计方法。

本文提出的SCMA 码本的优化方法是在母星座和扩频矩阵的基础上，讨论其中存在的带优化参数，取不同的参数值来设计算法进行仿真，并对母星座不同的维度的旋转角度进行算法优化，使得资源块上星座上的星座点之间尽可能分离开，以达到设计目的，让系统整体误码率性能都有明显改善。

1 SCMA的系统及码本设计

1.1 SCMA系统

可以考虑一个下行链路的SCMA 系统[12]，其中基站与共享K个资源元素的J个用户通信。每个用户的信号分布在K个资源元素上，且在正交场景下（J≤K），以确保每个用户可以享受正交资源元素，而在非正交的情况下（J＞K），过载率为，SCMA编码器包括星座函数fj和映射矩阵Vj两部分，对于星座映射函数fj将用户j发送的比特数据bj映射为N 维复星座点，大小为M；再通过扩频矩阵Vj将N 维星座点映射到码本Yj中的K 维复稀疏码字xj，最后用户j的码字可以表示为：Yj=Vj fj(bj)，则J个用户在K个正交资源块上传输信息的下行SCMA 通信系统具体如图1 所示。

图1 下行链路的SCMA通信系统

观察图1 可以看出，SCMA 编码器是从log2(M)位到大小为M的K维复码本Yj，且Yj=[x1j,x2j,…,xKj]T，M=|Yj|表示为码本的大小，且Yj具有N(N＜K)个非零元素的稀疏向量[13]，由图1 也可以看出，是六个用户在四个资源块上传输，则对应的因子矩阵F为：

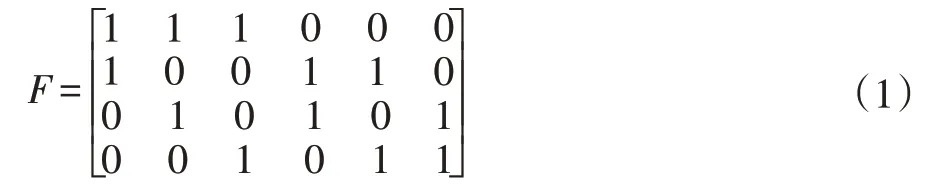
矩阵也可以用包含资源节点与用户节点的因子图表示，如图2 所示。

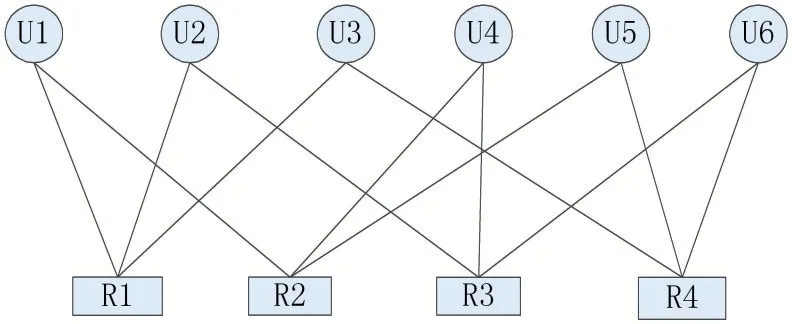
图2 SCMA码本因子图（矩形方块表示资源块）

图2 SCMA码本因子图（矩形方块表示资源块）

对于资源块上n的信号，经过信道传输后的接收信号y=(y1,y2,…,yk)可以表示为：

1.2 码本设计

高斯信道下简易SCMA 码本设计分为四个部分，包括构造映射矩阵，设计各用户星座图，设计星座矩阵和生成码本[14]，其中设计星座矩阵是至关重要的一步，它是通过各资源块上的有效用户星座再结合映射矩阵F产生，星座矩阵可以CMn,k表示为N×M的形式，对于经典的SCMA 码本设计，给定结构ζ(V,G;J,M,N,K)，其中，m是给定的设计准则，SCMA 码本设计问题[15]可以定义为：

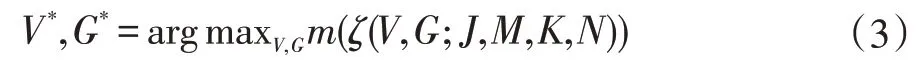
但这里的m没有具体的定义，所以上述问题不易得到最优解，不过可以通过多层最优方式来获得一个次优解，将映射矩阵V和星座函数集G分开设计，本文将码本优化重点放在星座函数集的设计上。

在SCMA 系统中，每个用户都有独一无二的码本，这意味着在设计码本时，会生成J个不同的星座，由于此过程较为繁琐，研究者一般先设计一个母星座，然后通过对母星座进行特定的运算，从而生成每个用户独特的码本，常见的设计准则包括最大化最小欧氏距离和最大化最小乘积距离，在用户数较少的情况下，能有较好的性能，当接入用户数较多时，通过引入不同维度间的相关性，以便恢复干扰的码字，码字间的功率差异也可以增加各资源块复用层上的远近效应，由于传统旋转交织码本的母码本在不同维度上并不存在功率差异，所以为了在该母码本上引入功率差异这一条件，经过码本研究者进一步研究，提出了星型正交幅度调制码本（StarQAM）[16]。

2 星型正交幅度调制码本优化设计

2.1 星型正交幅度调制码本简介

星型正交幅度调制码本（StarQAM）的母星座为：

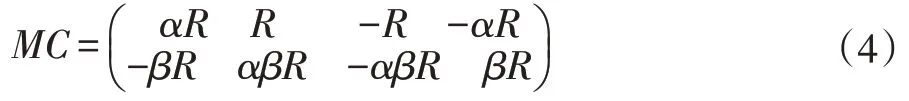
其中α以 及β是母星座的参数，且

另外，关于星型正交幅度调制码本的扩频矩阵为：

在扩频矩阵V中，其中e1,e2,e3表示母星座的第一维度、第二维度以及第三维度，所以e1jθ1表示母星座第一维度顺时针旋转θ1角度，表示母星座第二维度顺时针旋转θ2角度，e2jθ3表示母星座第二维度顺时针旋转θ3角度。这里的旋转角度θ1,θ2,θ3待优化的参数，注意我们的设计目标就是使得资源块星座上的星座点之间尽可能分离开来，已达到优化的目的。

所以，星型正交幅度调制码本的具体结构如下：

其中j表示第j个用户或者层j=1,2…,J，Vj以及CBj分别表示第j个用户的扩频矩阵和码本。

2.2 星型正交幅度调制码本初始分析

（1）理论分析

从星型正交幅度调制码本的结构可以观察出，其中参数α以及β是影响母星座性能的重要因素，其直接影响着母星座的最小欧氏距离以及功率差异，其母星座标准化最小欧氏距离：

另外，关于母星座存在的功率差异，可表示为：

观察上述公式可以看出，随着β的上升，标准化最小欧氏距离K在不断减小，而母星座功率差异在不断上升，因此两者之间的权衡在于β的选取，即β是影响两者的关键因素，所以在仿真不同β下，星型正交幅度调制码本的误码率也会存在差异。由于标准化最小距离为：

则当1 ＜β＜2 时，即β-1 ＜3-β，有：

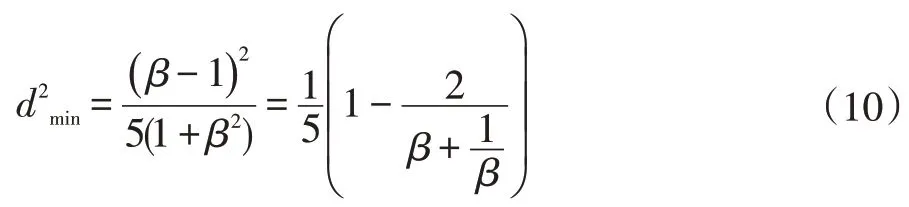
由上式可知，当β逐渐上升时，在不断上升，β=2 时，

当β＞2 时，有β-1 ＞3-β，有：

通过对上式求导我们可以发现，d2min在(2,3)上递减，在(3,∞)上递增。

所以综上所述，d2min在β=2 时取得最大值，即

（2）数值计算

将星型正交幅度调制码本（StarQAM）的母星座展平可得：

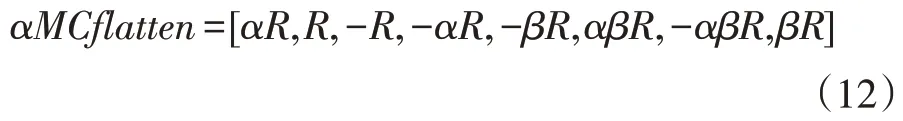
根据母星座展平式，对其中参数α和β设计算法如下：

Algorithm1:StarQAM mother constellation parameters [α]and[β]design algorithm

1:input MCflatten

1:initialization:α=1,β=1,global_dmin=0

2:whileβ≤uβdo

3:β=β+δβ

4: whileβ≤α≤uα

5:α=α+δα

6: calculate dmin for MCflatten

7: if dmin＞global_dmin

8: global_dmin=dmin

9: opt_para=[α,β]

10: endif

11: endwhile

12:endwhile

13:output global_dmin,opt_para

Note:uα=uβ=5 andδα=δβ=0.1for this simulation

算法1：StarQAM 母星座参数α和β设计算法

通过算法1 的求解，当α=3，β=2 时母星座8 个点最小距离最大，数值计算结果符合预期。

2.3 星型正交幅度调制码本中旋转参数优化

为了进一步提高性能，需要对旋转参数进行优化，对码字元素用一种方式来叠加，以最大限度地提高所得到的星座点的距离，由于每个资源块在解码过程中都有一定的贡献，因此也是决定性能的因素之一，基于每个资源块最小正则化距离之和的平均值，则生成的码本统一度量为：

其中的K表示资源块，这里的表示最低限度，由于i 表示资源块数目，则有：

由星型正交幅度调制码本的扩频矩阵（5）可以发现，其中待优化的参数包括θ1,θ2,θ3，而旋转参数的设计目标是使得各资源块上点尽可能分散（合成之后的星座点），具体算法如下：

Algorithm 2:RE constellation parametersα和βdesign al⁃gorithm

1:input MC,V

2:initialization:θ1=θ2=θ3=0,global_dmin=0

3:whileθ1≤1

4:θ1=θ1+δ

5: whileθ1≤θ2≤1

6:θ2=θ2+δ

7: whileθ2≤θ3≤1

8:θ3=θ3+δ

9: calculatedmin,i.e.,,其中表示第k 个资源块的第i 个合成的星座点，表示第k 个资源块第i 个合成星座点与其他星座点之间的距离平方之和，表示第k 个资源块所有星座点距离平方和中的最小值，，dmin表示所有资源块最小距离的平均值。

10: ifdmin＞global_dmin

11: global_dmin=dmin

12: opt_para=[θ1,θ2,θ3]

13: endif

14: endwhile

15: endwhile

16:endwhile

17:output global_dmin,opt_para

Note:δ=0.1

算法2 RE 星座参数设计算法

通过算法2 的计算，当θ1=0，θ2=θ3=0.5 时各资源块星座点（合成后）分布最分散。

3 数值和模拟结果

在本节中，将通过仿真结果和分析结果来说明基于星型正交幅度调制的SCMA 码本优化，首先，仿真不同β下，SQ 码本的误码率：

β=1.2 时BER = [0.2671 0.2132 0.1450 0.0743 0.0251 0.0050 5.28e-4 1.75e-5 0];

β=1.59 时，BER = [0.2713,0.2162,0.1483,0.0769,0.0253,0.0045,3.71e-4,2e-5,0];

β=2 时，BER = [0.2735,0.2179,0.1511,0.0802,0.0271,0.0048,3.64e-4,8.33e-6,0];

β=2.6 时，BER = [0.2747 0.2189 0.1533 0.0844 0.0307 0.0061 5.22e-4 1e-5 0];

得出不同β下仿真的误码率曲线如图3。

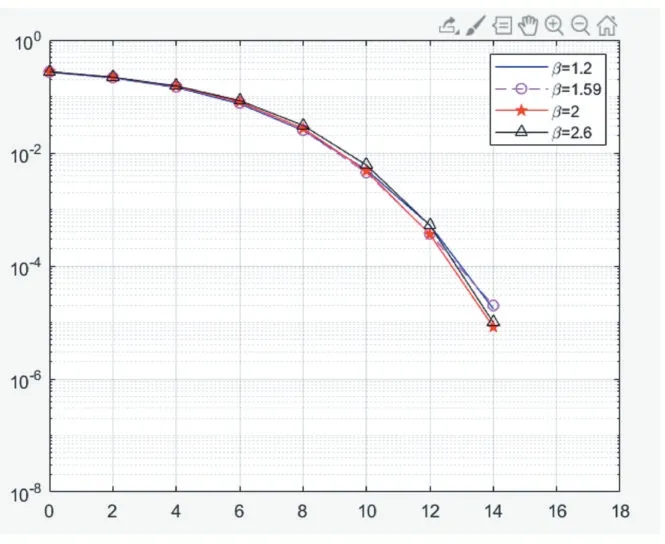
图3 不同β 下误码率比较

从图3 中可以看出，随着β的上升，误码率在不断下降，当β=2 时误码率性能最优，在高信噪比下显著优于文献[15]提出的β=1.59。当β超出2 时，随着β的上升，误码率在不断上升。另外值得注意的是，虽然β=2.6 在低中信噪比下均表现较差，但是在高信噪比下出现明显改善。

从上节分析可以看出，不同β下SQ 码本资源块星座图（未叠加之前），RE2、RE3 资源块上x 轴上分布着母星座8 个点，第二维的最小点与第一维最小点距离随着β的变化而变化，因此需要讨论不同的β值来确定一个中间值，使得第二维的最小点与第一维最小点以及最大点之间的距离都足够大，具体的仿真结果如图4 所示。

图4 β=1.59

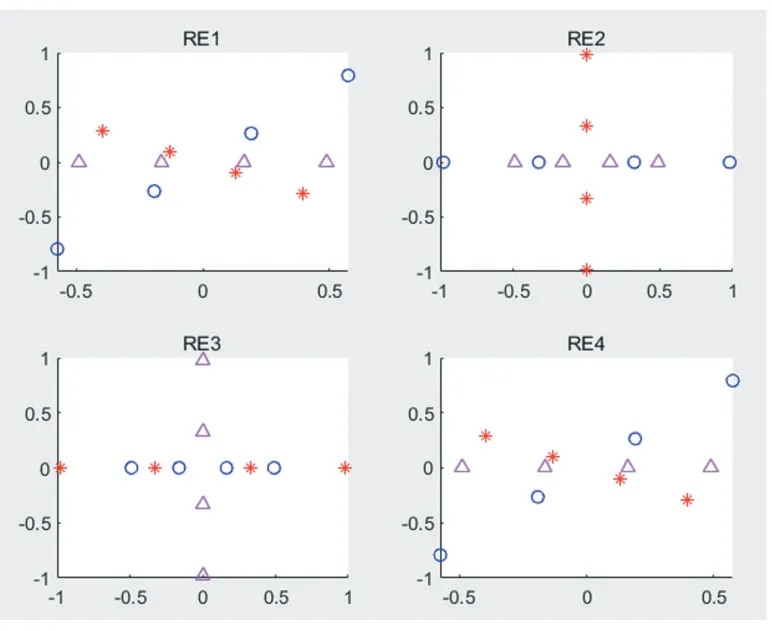
图5 β=2

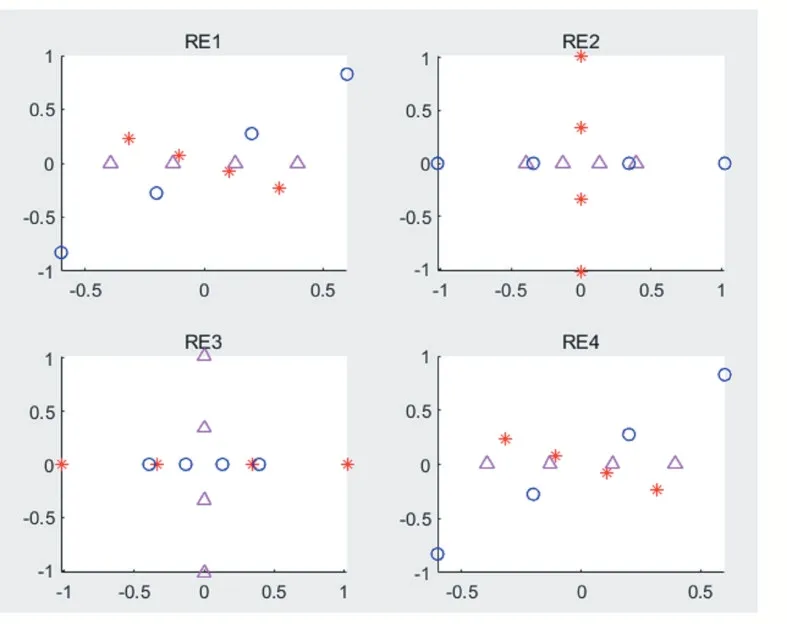
图6 β=2.6

比较图6、图7 和图8 可以看出，随着β的上升，第二维的最小点与第一维最小点距离在逐渐增大，但是当β超出一定值时，β变大使得母星座第二维的最小点与第一维的最大点间的距离在逐渐减小，也应证了算法1，当α=3，β=2 时母星座8 个点最小距离最大。

按照上述介绍的原则，我们对本文提出的优化旋转角度进行了误码率仿真，具体结果如图7。

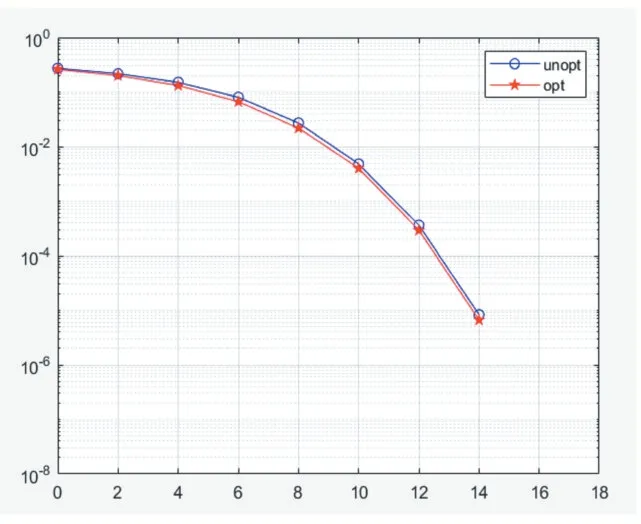
图7 旋转角度优化前后误码率比较

从图7 中可以看出，优化后的旋转角度，使得各个资源块上的星座点尽可能分散，可以使得误码率进一步下降。

4 结语

本文基于星型正交幅度调制提出了一种新的优化码本设计，通过对母星座展平式来对其中的参数α和β进行算法设计，从而得到当α=3，β=2 时母星座8个点最小距离最大，并通过优化旋转参数，使得各资源块上点尽可能分散（合成之后的星座点），讨论了不同的β值确定了一个中间值，使得第二维的最小点与第一维最小点以及最大点之间的距离都足够大，以达到降低系统误码率的目的，本文设计的优化码本方法在高信噪比下表现优良，研究使得误码率在不断下降，得到当β=2 时误码率性能以达到最优。