环形肋片导热问题的数值模拟
袁炳志,石文,任书衡
(华北电力大学能源动力与机械工程学院,保定071000)
0 引言
数值模拟是计算机技术在工程上最为广泛的应用之一,其依靠电子计算机,结合有限元的概念,通过数值计算和图像显示的方法,对工程问题和物理问题的研究与求解。在换热设备中,通常使用肋片增大传热面积、降低热阻,从而提高传热效率。环形肋片可以布置在圆管上,有着优良的导热性能,但在分析求解中,由于环肋与普通直肋的区别,不能直接进行理论计算,需要借助数值模拟求解[1]。
本文基于显式和隐式两种离散方式对传热方程进行离散,利用MATLAB 通过高斯-赛德尔迭代和雅各比迭代两种迭代方式计算了环肋的稳态传热和瞬态传热的问题。通过比较肋效率、传热量和温度场,对离散方式和迭代方式进行比较和分析。
1 稳态问题数值求解
1.1 数学模型的建立
1.1.1 问题分析
已知肋根处的温度t0高于肋片附近的流体温度tf,热量由肋根处向肋端处导热,同时肋片表面和周围空气存在对流换热。
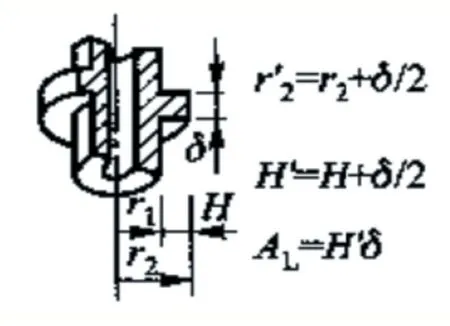
图1 环肋的物理模型
严格来说,肋片的导热问题为圆柱坐标系下三维非稳态导热问题,肋片内部的温度场为三维的温度场t=f(r,ϕ,z,τ),则其一般形式的导热微分方程为[2]:

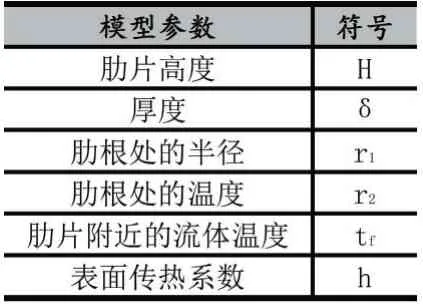
表1 符号说明
要分析一般情况下环肋的导热问题,需要对该式进行简化:
(4)由于通过肋端的散热量很小,肋端可看作绝热。但是为了减少计算带来的误差,对肋高进行修正。修正后肋高
(5)肋片表面的热量传递不能忽略,把表面传递的热量折合成虚拟内热源Φ̇:
导热微分方程中的内热源项由微元段表面的对流传热量折算得到[3]。沿肋高方向任取dr 作为研究对象,则该微元段表面总散热量可以表示为:
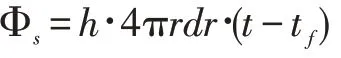
可得虚拟内热源强度为:
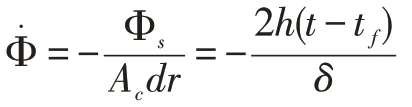
在工程应用中,Bi<0.1 则认为肋片的温度分布符合一维假设。计算可得Bi=0.0005 满足所需条件。
通过以上的假设分析,可以把导热微分方程简化为圆柱坐标系下一维有内热源的稳态导热问题。则其导热微分方程为:

边界条件为:
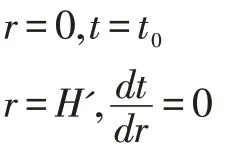

1.1.2 离散方程的建立
所研究问题的导热微分方程是一个二阶非齐次常微分方程,为转化成齐次方程便于求解,引入无量纲过余温度和无量纲半径;为便于采用特征方程求解,令。导热微分方程可进一步化简为:
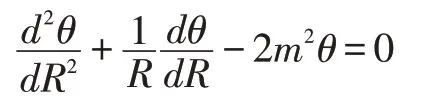
对环肋进行空间区域离散化,取空间步长Δr,在半径r 方向上取N 个节点,节点编号为n=1,2,3,…,N-1,N。离散化过程中采用二阶精度泰勒展开的中心差分格式,建立离散化方程:
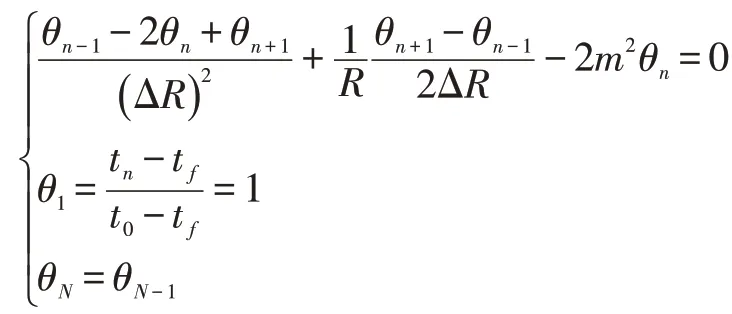
也可以推知肋效率表达式:
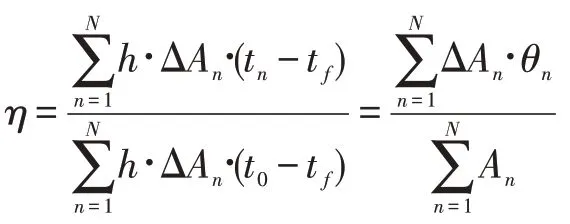
1.1.3 求解方法
将离散方程简化整理,可得:
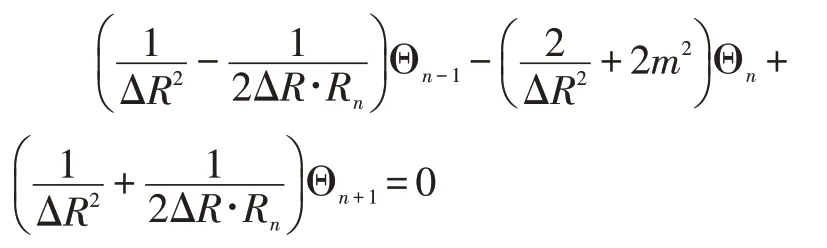
为方便编程求解,将化简后的离散方程式表示为Aθ=b的形式,其中A 为N×N的系数矩阵,θ是列向量,表示无量纲过余温度。在MATLAB 里定义系数矩阵后,对特殊元素进行赋值,使其满足离散化方程。并调用Gauss-Seidel 迭代函数进行数值计算,求得无量纲过余温度场,最终得到温度场。

1.1.4 网格无关性验证
根据MATLAB 模拟的程序,在控制r2'/r1以及m 不变的情况下,任意输入节点数N,可以得到不同的肋效率η的值。下表列出了在r2'/r1=2 且m=1.5 的情况下,节点数N 分别取20、30、45、60、100、150、200 时肋效率的值:

表2 肋效率的值
由表2 可知,在不同的节点数N 的情况下,肋效率的前两位小数可以控制不变,但是当N 取到150 及以上时,肋效率的前四位小数可以控制不变。这时可以认为数值计算的结果基本与网格数无关,即实现了网格无关性验证。
1.2 模型的求解与分析
1.2.1 求解代码
输入:r2'/r1、m、节点数N
输出:温度场矩阵t、肋效率efficiency、传热量fi1
k=input('请输入r2/r1 的值.');
disp(['r2/r1=',num2str(k)]);
N=input('请输入节点数N 的值.');
disp(['节点数N=',num2str(N)]);
m=input('请输入参数m 的值.');
disp(['参数m=',num2str(m)]);
dR=1/(N-1);%定义无量纲半径的步长
R=zeros(N,1);%无量纲半径矩阵
for i=1:1:N
R(i)=1/(k-1)+(i-1)/(N-1);%为无量纲半径赋值
end
b=zeros(N,1);%定义一个N 行1 列的零矩阵,作为迭代求解时等式右边的矩阵。
b(1)=1;%边界条件1:Θ1=1。
theta0=ones(N,1);%设置无量纲过余温度场Θ的迭代初值。
A=zeros(N,N);%定义系数矩阵A。接下来对特殊元素赋值。
A(1,1)=1;%同样是为了满足边界条件1:Θ1=1。
for i=2:1:N-1
A(i,i-1)=(1/(dR^2))-(1/(2*dR*R(i)));
A(i,i)=-(2/(dR^2))-2*m^2;
A(i,i+1)=(1/(dR^2))+(1/(2*dR*R(i)));
end%此循环为系数矩阵A 赋值。
A(N,N-1)=-1;
A(N,N)=1;%以上两个赋值是为了满足边界条件2:ΘN-ΘN-1=0。(即顶端绝热条件)
theta=gaussseidel(A,b,theta0);%调用高斯—塞德尔迭代函数。
%以下开始计算肋效率
a1=0;
a2=0;
for i=2:1:N-1
a1=a1+R(i)*theta(i);
a2=a2+R(i);
end
a1=a1+R(1)/2*theta(1)+R(N)/2*theta(N);
a2=a2+R(1)/2+R(N)/2;
efficiency=a1/a2;%肋效率
disp(['以下为计算结果:'])
disp(['肋效率为:',num2str(efficiency)]);
%以下为计算传热量和温度场
h=50;
r1=0.01;
r2=0.04;
t0=100;
tf=20;
fi1=a1*2*pi*(r2-r1)^2*dR*(t0-tf)*h;
t=theta*(t0-tf)+tf+273.15;
1.2.2 求解结果

表3 具体参数
(1)温度分布和传热量
在MATLAB 中利用高斯赛德尔迭代法进行计算,在r2'/r1=4.1 以及m=0.49015,节点数N 取150 的情况下对各点处的温度进行求解,得到肋片传热量为15.135W,同时对比Fluent 各点处的温度分布如表4。
将MATLAB 中获得温度场导出为dat 文件,导入Tecplot 里分别绘制出MATLAB 以及Fluent 的温度分布图像如图2a、图2b 所示。

表4 温度在不同节点位置的分布情况
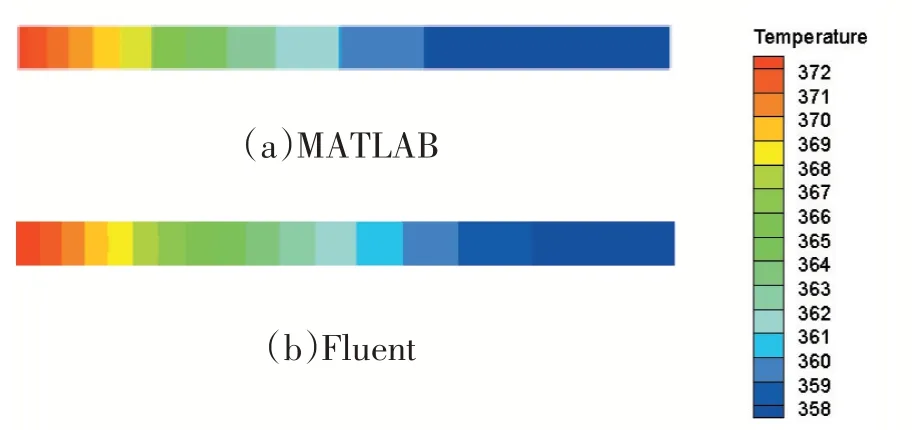
图2
得到整体的温度分布曲线为图3。
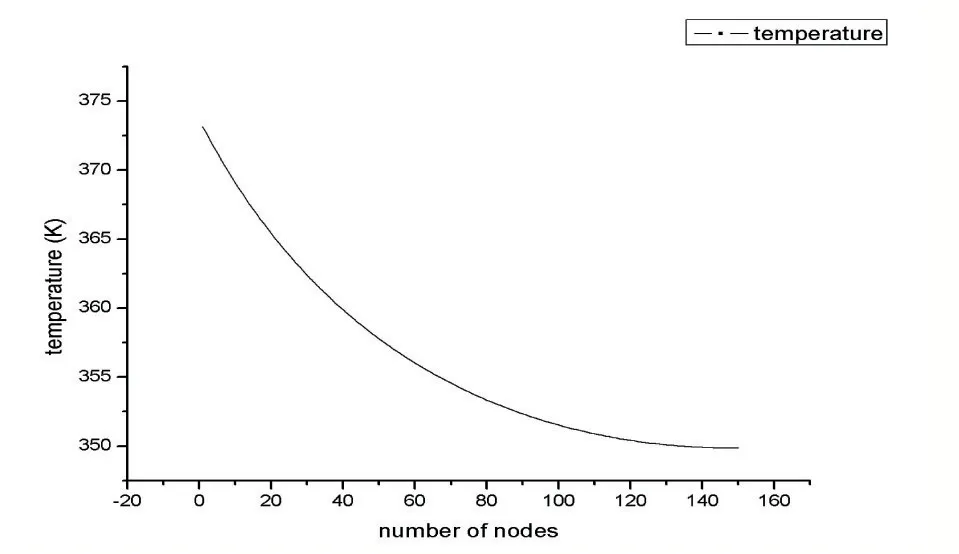
图3 温度分布曲线
由上述图表可以看出:
随节点坐标的增加,越靠近肋端处温度越低,并且在传热过程中温度变化的斜率逐渐减小,说明温差降低使传热速率降低,传热量逐渐减少,与定性分析的结果相符。因此推测:在一定范围内,增加肋片高度可以使肋端温度进一步降低,增加肋片的传热量,但同时肋效率也降低。
MATLAB 和Fluent 得到的温度分布情况十分接近。两种方式获得的肋端处温度分别下降到了350.0562K 和357.1077K,相对误差约为2%,误差较小,结果较为精确,与定性分析的结果相符。进一步证明了MATLAB 模拟结果的可信度与精确度。
(2)肋效率
根据网格无关性的验证结果,取N=150 分别计算了当r2'/r1为2、3、4.1、5,m 为0.1、0.5、1、1.5、2、2.5 时肋效率的值:
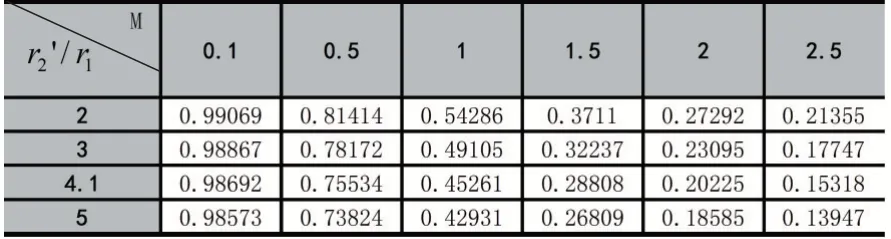
表5 不同r2'/r1 和m 情况下肋效率的值
①根据表中数据,绘制r2'/r1=2 的图线与教材中给出的图线做对比。

图4 r2'/r1=2 时的η-m 曲线图
曲线actual(教材中的图线)与simulated(模拟的曲线)高度拟合,说明上述编译的解决方案精确度很高,可以用来求解所述案例。
②根据表中数据绘制r2'/r1=4.1 时的η-m曲线图。
肋效率的物理意义为实际散热量与假设整个肋表面处于肋基温度下的散热量之比。根据r2'/r1=4.1的图线可得:m 越小即肋高越小,肋片表面的平均温度越接近肋基温度,肋效率就会越大。对比所有的曲线可得:r2'/r1的值越小,在m 相同的情况下肋效率的值越大。所以,适当减小。r2'/r1和m 可以增大肋效率,但会减小散热量。
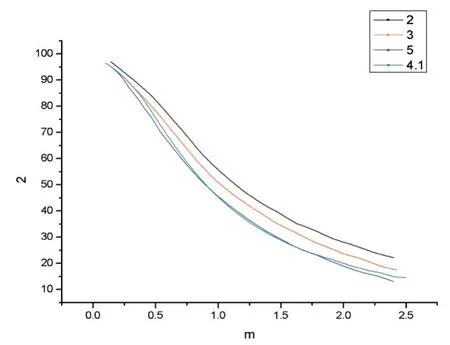
图5 不同r2'/r1 时的η-m 曲线图
2 非稳态问题数值求解
2.1 数学模型的建立与求解方法
由于对于稳态问题的求解,采取泰勒级数展开法进行离散化,为了与稳态的结果相印证对比,并比较两种离散方式的差异,采用控制容积热平衡法来对非稳态问题进行离散化处理。该方法是根据每个节点所代表的控制容积的能量守恒关系,得到该节点与相邻节点温度间的关系式。在离散方程中,空间步长为Δr,时间步长为Δτ。为满足稳定性条件,时间步长取0.0005s。
(1)采用显式格式离散方程得:
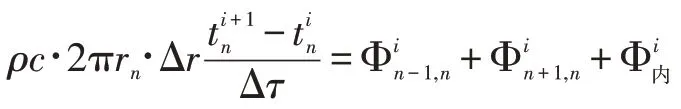
其中:

化简得:
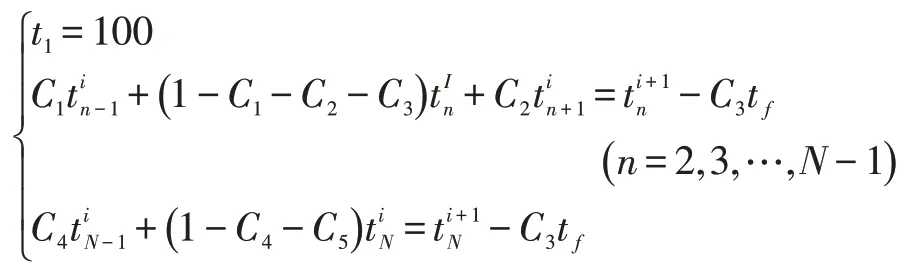
其中:

至此得到非稳态问题的显式离散方程和相应边界条件。采用高斯—赛德尔方法对方程进行迭代处理,可以求得非稳态问题的温度场变化。
(2)同理可求得隐式格式离散方程

为方便MATLAB 求解,将方程组转化为如下形式:
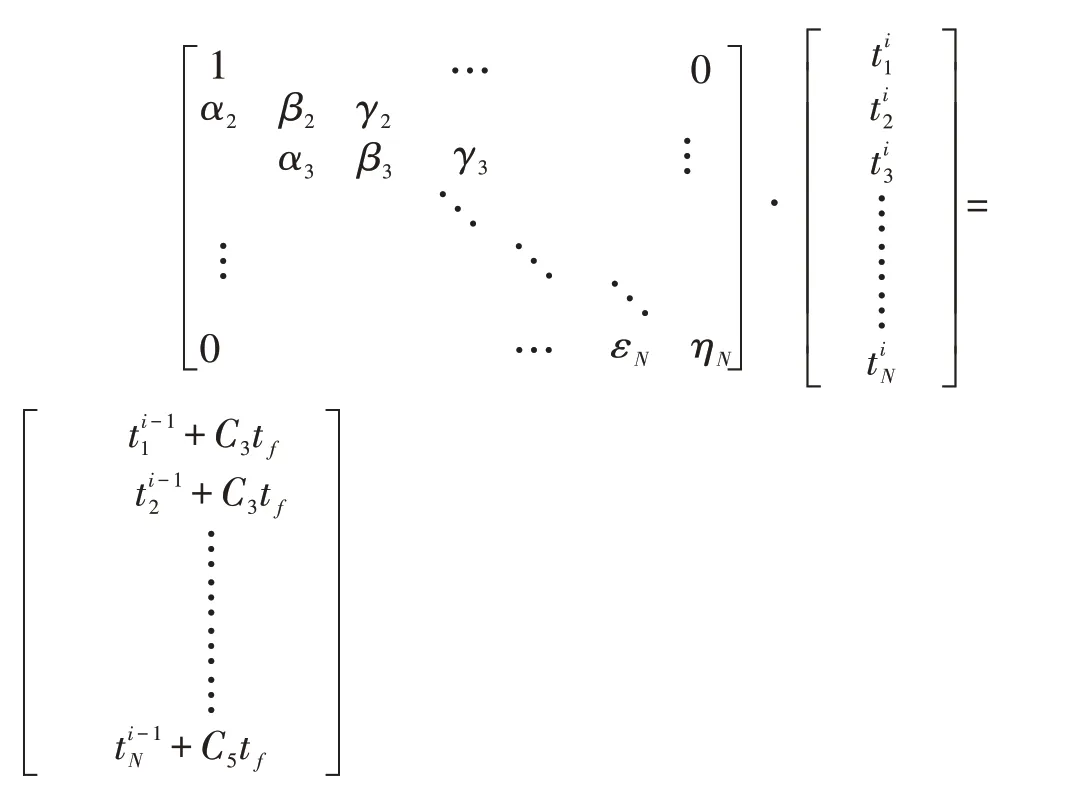
即:
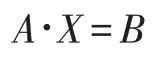
这样一来,就把求解温度分布的问题转化为求解X 列向量的问题,便于编程计算。在稳态问题的求解中,运用高斯赛德尔迭代,运用两种迭代方法求解方程,并比较温度场的差异。对于高斯赛德尔迭代,利用先前构造的高斯赛德尔迭代函数即可求解。
对于雅各比迭代,由于初始温度已知,则可求出等式右边列向量B,利用X=A/B 可以求得下一时层中X的值,将其赋值给B,形成迭代计算,最终求得温度场。
%参数设定
h=50;
a=0.00004115;
N=10;
r1=0.01;
r2=0.041;
tf=20;
delta=0.002;
%定义空间步长,并通过迭代得出半径矩阵
dr=0.031/(N-1);
r=zeros(N,1);
for i=1:1:N
r(i)=r1+(i-1)*dr;
end
dtime=1/20;%定义时间步长
tt=20*ones(N,1);%初始温度
tt(1)=100;%边界条件
t=ones(N,1);
counter=0;
while counter<=1000000
t(1)=100;
counter=counter+1;
for i=2:1:N-1
t(i)=(a*(r(i)-dr/2)*dtime/(r(i)*dr*dr))*t(i-1)+(1-(a*(r(i)-dr/2)*...
dtime/(r(i)*dr*dr))-(a*(r(i)+dr/2)*dtime/(r(i)*dr*dr))-(2*h*dtime/(0.002*270...0*900)))*tt(i)+(a*(r(i)+dr/2)*dtime/(r(i)*dr*dr))*tt(i+1)+((2*h*dtime/(0.002...*2700*900))*tf);
end
t(N)=(a*(r2-dr/2)*dtime/(dr*r2*(dr/2)))*t(N-1)+(1-(a*(r2-dr/2)*dtime/...
(dr*r2*(dr/2)))-(2*h*r2*dtime/(0.002*2700*900)))*tt(N)+(2*h*r2*dtime/(0.002*...2700*900))*tf;
tt=t;
end
t=t+273.15;
2.2 结果分析
2.2.1 温度随时间变化
在MATLAB 中显式格式采用高斯—赛德尔迭代法进行计算,在r2'/r1=4.1,节点数N 取100 的情况下对各点处的温度进行求解,同时对比Fluent 各点处的温度分布可得温度随时间的变化图像(图6)。
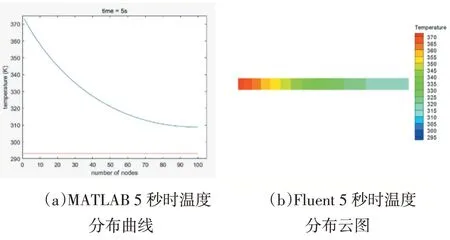
图6
从温度曲线可以看出靠近肋基的地方温度下降的较快,靠近肋端的地方温度变化较为平缓,越靠近肋端温度越低,说明在温差大的情况下,传热的效果强。
显式格式与Fluent 对比如图7,以5s,25s,50s 时刻为例,温度场的相对误差均在1%以下,误差较小,并且随着时间的推移,各个节点的温度不断升高,直到50s左右温度分布基本不变,非稳态过程趋于稳定,此时温度分布情况与稳态的温度分布情况近乎一致,肋端处的温度都约为350℃。

图7 不同时刻MATLAB与Fluent温度分布曲线
2.2.2 显式差分、隐式差分比较
在求解显式差分格式的问题中,从MATLAB 中导出温度分布随时间变化的视频,可以看出温度上升的过程先快后慢。这是由于最一开始温差较大,传热量大,温度变化大,后来随着温度逐渐升高,温差越来越小,传热量减少,温度场的变化也越来越慢。到50s 以后温度变化很小,温度场几乎不变,此时稳态和非稳态的温度场分布几乎一致,相对误差小于1%。
温度分布在肋基处温度最高,越靠近肋端处温度越低,并且在显隐式情况下求解得到的结果十分接近。而显式与隐式的差别就是对时间的向前向后差分,所以对同一问题所得结果极为接近,这说明了上述模型符合预期,能达到模拟该案例的水平。
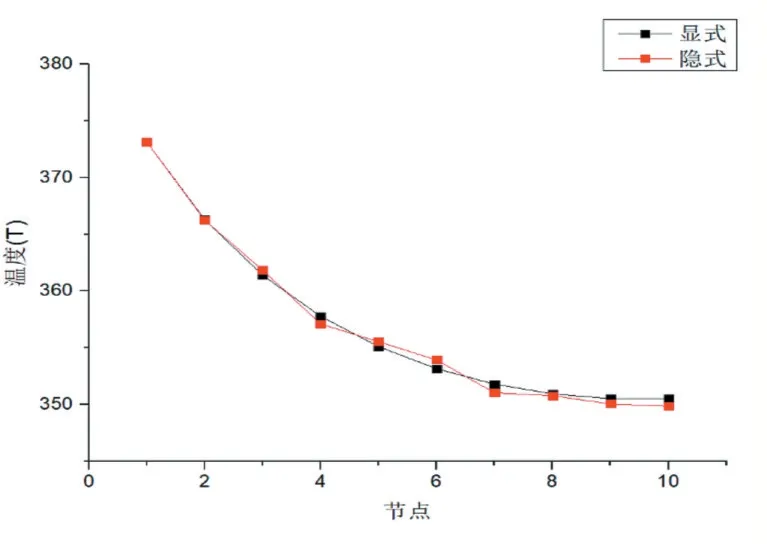
图8 50秒时,显式和隐式差分温度分布对比图
2.2.3 雅各比迭代和高斯赛德尔迭代比较
为比较两种迭代方法,取10s 时的温度场进行对比,如图9 所示。可以看出采用两种迭代方法对该问题的影响很小。
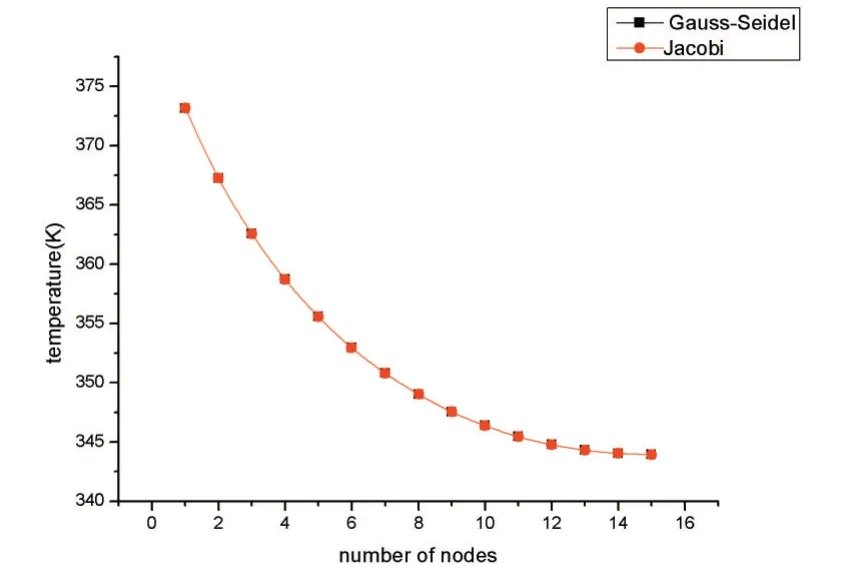
图9 10秒时,雅各比迭代和高斯赛德尔迭代温度分布对比图
2.2.4 传热量随时间变化
图9 为MATLAB 中传热量随时间变化的曲线,从图中可看出开始阶段温差大,导致热流量变化大,之后温差逐渐减小,传热量趋于平缓。为对比验证,做一条传热量为15.135W 的直线,50 秒以后非稳态的传热量与稳态的传热量完全重合,相对误差为0.2%。
在50s 之前传热量不断增加,起初传热量变化较大,之后逐渐平稳,趋近于一个稳定值,可以认为近乎达到了稳态。通过观察温度变化曲线可知,初始时刻温度变化较大,50s 后温度几乎不变,可以看做稳态情况下的温度分布。温度分布情况与稳态时求解结果相近,肋端处温度均为350℃左右。同时在非稳态传热过程中,由于肋基温度不变,热量逐渐从肋基传到肋端,并散失到外界,离肋基越远,温度越低,温差越小,温度分布曲线趋于平缓,符合理论分析。
3 结果分析与总结
对于稳态问题,通过简化和合理假设,先推导出了环肋一维有内热源的导热微分方程,进一步进行无量纲化并采用泰勒级数展开法中心差分格式进行离散,利用MATLAB 求解温度场和传热量,并计算相应的肋效率。对于非稳态问题,利用控制容积热平衡法进行空间区域离散,并分别运用显式差分和隐式差分对时间区域离散,对于隐式差分分别采用高斯—赛德尔迭代和雅各比两种迭代方式进行计算和比较。结果总结如下:
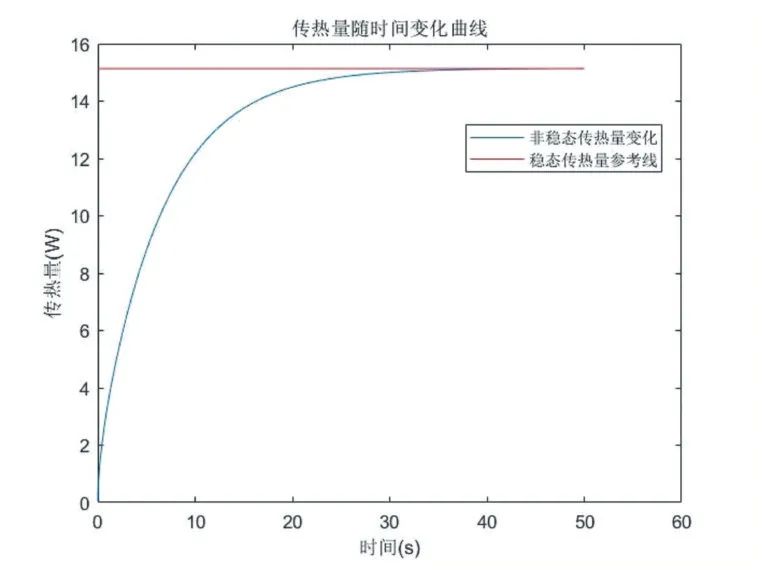
图10 MATLAB传热量变化曲线
●MATLAB、Fluent 模拟所得温度场分布一致,肋端温度在350K 左右,相对误差不超过2%。靠近肋基处温度下降较快,靠近肋端处温度变化较为平缓,越靠近肋端温度越低。增大肋高会增大散热量,降低肋效率。
●非稳态状况,MATLAB 所得显式与隐式结果一致,不同节点在5s,25s,50s 的温度数值与Fluent 模拟结果相对误差不超过1%。取10s 时温度场对比,雅各比迭代和高斯赛德尔迭代结果也无差别。
●非稳态下传热量随时间增加,增长速率逐渐降低,50s 左右后与稳态散热量保持一致,相对误差为0.2%。

