K频段斐波那契网格稀疏阵列分析与设计*

温 剑，阳 昆，姚亚利，侯禄平

(中国西南电子技术研究所，成都 610036)

0 引 言

在国内外近年来蓬勃发展的K/Ka频段(大约20～30 GHz，非严格定义)低轨卫星通信网络有源相控阵天线领域，由于卫星轨道高度较低(1 000 km左右)，要求采用高增益波束宽角扫描(≥±60°)形成对地球覆盖。采用均匀网格排布(矩形、正方形、三角形)的常规阵列受到栅瓣条件的严格限制，其阵间距接近半波长。而目前国内受射频芯片技术的限制，在高成本高可靠性的卫星平台上仍主要采用具有高输出功率、低噪声系数、抗辐照特性的砷化镓(GaAs)芯片，但GaAs工艺集成度不高，射频芯片尺寸与阵间距相当。另外卫星平台资源紧缺，对K/Ka频段相控阵天线提出多波束、多功能化的要求，常规阵列难以在5～8 mm的间距下排布多波束芯片及合成网络。K/Ka频段常规阵列电路布局设计和加工制造带来非常大的困难，严重制约了K/Ka频段卫星通信有源相控阵天线向多波束、低剖面、数字化、低成本化发展，工程中对阵列大间距稀疏设计提出了迫切的需求。

K/Ka频段有源相控阵高密度的电路、芯片集成，也要求稀疏阵列网格具有宏观上的均匀性，便于阵元与芯片位置匹配。K/Ka频段通信大瞬时带宽要求各射频通道长度差异小，尽量减少高成本高损耗的延时器的使用。在稀疏阵布局设计时应全局考虑以上通信用有源相控阵的特殊要求。

满阵的副瓣和栅瓣是由于阵元的周期排布形成的。稀疏阵设计的核心，就是采用密度加权(规则网格点随机采样)、位置随机等手段破坏周期性，达到降低副瓣峰值、抑制栅瓣的效果，同时保证增益等核心指标达到门限值。工程中常采用遗传算法、粒子群算法等全局优化算法寻找的最佳的随机阵列分布，由于没有明显的数学物理对应关系，导致在设计阵元数超过几百的大规模阵列时，未知量大、计算量大、收敛慢[1-4]。为了减少计算未知量常常对阵列做简化，如子阵块随机布阵[5],但子阵化也会造成附加的周期性，使栅瓣和旁瓣恶化。

圆环阵是另一种常用的稀疏阵列设计方案[6]。圆环阵在极坐标中以一定的规律排布，所以优化调整参数较少，设计较为方便快捷，易于形成在直角坐标中无序的排列，达到栅瓣抑制效果，但是平均副瓣电平较高。环形稀疏阵的优化参数有圆环半径递增量、单圈圆环上等角分布的单元数量、每圈单元起始位置角度等。对于小规模圆环阵，可使用遗传算法优化对上述参数进行搜索寻优。由于在每一步优化过程中要对多个指向的方向图积分再计算代价函数，其计算量巨大，优化效率仍相对较低。如要获得更低的副瓣则半径递增量较大[7]，导致阵元密度不均匀，不适合K/Ka频段宽带通信相控阵天线的要求。

如能跳出全局优化算法的框架，利用数学、物理、仿生学等理论，寻找稀疏阵列辐射特性与阵列布局的映射关系，将大幅提高稀疏阵列的设计效率。这种思想在电磁场及微波学科已有多种成功案例，比如螺旋天线的非频变超宽带效应[8]，分形几何的自相似性赋予天线的超宽带特性[9]。文献[10]介绍了一种斐波那契网格稀疏阵列设计方案，用于实现大间距阵列的栅瓣抑制。这种布阵方案由解析公式给出，无需使用如遗传算法这类大规模的数值计算，所以非常高效，在工程中可以大幅简化阵因子设计流程，直接跨入三维电磁场仿真。该文献在标准的斐波那契网格上叠加径向扩展因子构成密度加权阵，对旁瓣电平进行控制。

本文从积分变换和数论等数学原理上对斐波那契网格稀疏阵列的栅瓣抑制特性进行分析和解释。相比现有文献，增加了斐波那契网格的均匀性和无序性的理论分析，解释了斐波那契网格用于相控阵工程中天然具有栅瓣抑制特性的机理。另外，利用轻微的幅度加权进一步抑制旁瓣的分析，这和现有文献采用的密度加权稀疏化抑制旁瓣的方式相比有创新，也更匹配宽带K/Ka频段通信相控阵天线的需求。本文设计出的斐波那契网格稀疏阵列具有大间距、网格均匀、低副瓣、无栅瓣、宽角高增益的特性，在K/Ka频段有源相控阵工程中应用前景广阔。

1 基于斐波那契网格的稀疏圆阵设计

以上列举的卫星通信K/Ka频段相控阵天线稀疏化栅瓣抑制布局要求可总结为阵列网格无序、宏观均匀，在数学中被称为Tammes问题，即二维三维的装箱问题(Packing Problem)。用数学语言描述为：将点在平面或曲面上均匀铺开以达到各点的最小距离最大化[11]。六边形网格是平面Tammes问题的最优解，但网格有序，应用在大间距平面相控阵中时会出现栅瓣。

1.1 斐波那契网格定义

斐波那契网格是使用黄金分割比为角度增长系数的密绕螺旋，可以在球面或圆平面上生成无序且宏观均匀分布的点云[11-13]。

斐波那契网格具有简单的表达式[11]，以平面阵为例：

(1)

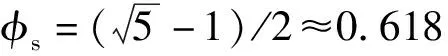
1.2 斐波那契网格均匀性解释

圆可以用极坐标和直角坐标表示[13]，其变换式为

(2)

直角坐标和极坐标进行积分变换的雅可比行列式为

(3)

则积分元为

(4)

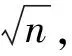
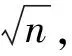
(5)

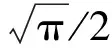
1.3 斐波那契网格无序性解释

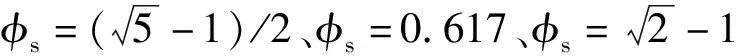
可以用数论的连分式展开理论[12，14]解释以上图形的周期性螺旋条纹。

任意一个实数a都可以展开为连分式：

(6)

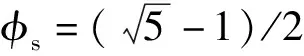
图1 斐波那契网格详图

把a的连分式在某一项截断，得到a的有理逼近，称为丢番图逼近(Diophantine Approximation)。如果截断到ak，化简后得到的最简分数为pk/qk。pk和qk可以有以下递推公式求得

pk=akpk-1+pk-2,

(7)

qk=akqk-1+qk-2。

(8)

式中：p0=a0，q0=1，p-1=1，q-1=0。定义逼近误差k=|qka-pk|。

φs=0.617的连分式为[0;1,1,1,1,1,1,3,21]，各阶丢番图逼近项与误差如表1所示。

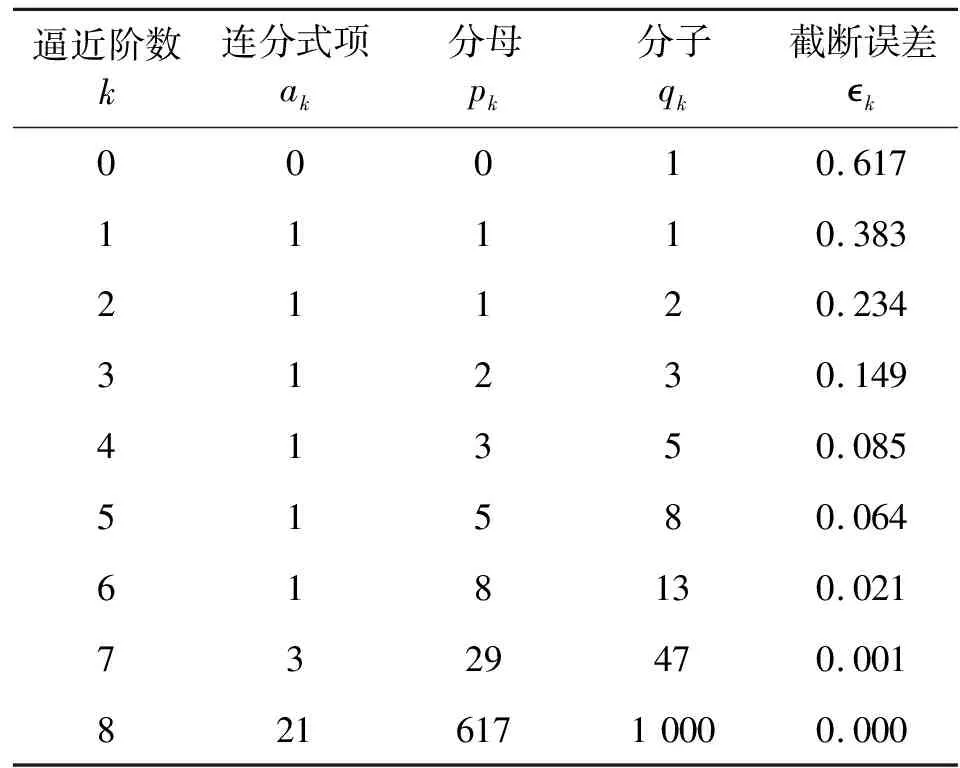
表1 0.617的各阶丢番图逼近项与误差

图2画出了φs=0.617时1～400点图形，可以看出，在原点附近点云形成较明显的13条螺旋臂，而在外围点云呈47条射线状，13和47是丢番图逼近的分母。将螺旋臂和射线的这种显著的排列称为模式，本图中的模式编号为8/13模式和29/47模式。

图2 φs=0.617的密绕螺旋详图

利用丢番图逼近，将无理数连分式截断，如产生截断项ai的激增，点云图中就会出现十分显著的模式。

黄金分割比的连分式项全为1，非常稳定，模式切换频繁但没有较大的突变，这种特性正是形成无序但宏观均匀分布点云的原因：均匀是因为在任何半径处各模式的差异非常小，不会出现大的间距；无序是因为每种模式都不会持续很久。

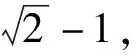
图的密绕螺旋详图

1.4 576元阵列数值算例

基于以上分析，斐波那契网格完美解决了平面点的均匀且无序地排列问题。根据阵列天线的栅瓣产生的机理[2]，我们认为采用斐波那契网格能对大间距阵列的栅瓣进行有效抑制。以下进行数值仿真，分析斐波那契网格及另外几种具有类似几何特性的网格对阵列的栅瓣、副瓣等指标的影响，找到其关键设计参数。

首先对工作在20 GHz的576元阵进行数值仿真[15]，分析其阵因子方向图。取不同的φs，并调整缩放比例使576元分布在半径0.3 m的口径中，等效间距DE≈1.48λ。阵列数值仿真结果如图4～6所示，采用天线工程中的uv空间投影方向图形式，便于观察整个上半空间的副瓣，其中心为法向，径向为俯仰角，周向为方位角，幅度采用归一化增益值，单位为dB。由于阵列规模较大，可以看出能实现相当于圆口径等副加权的-17 dB副瓣电平。

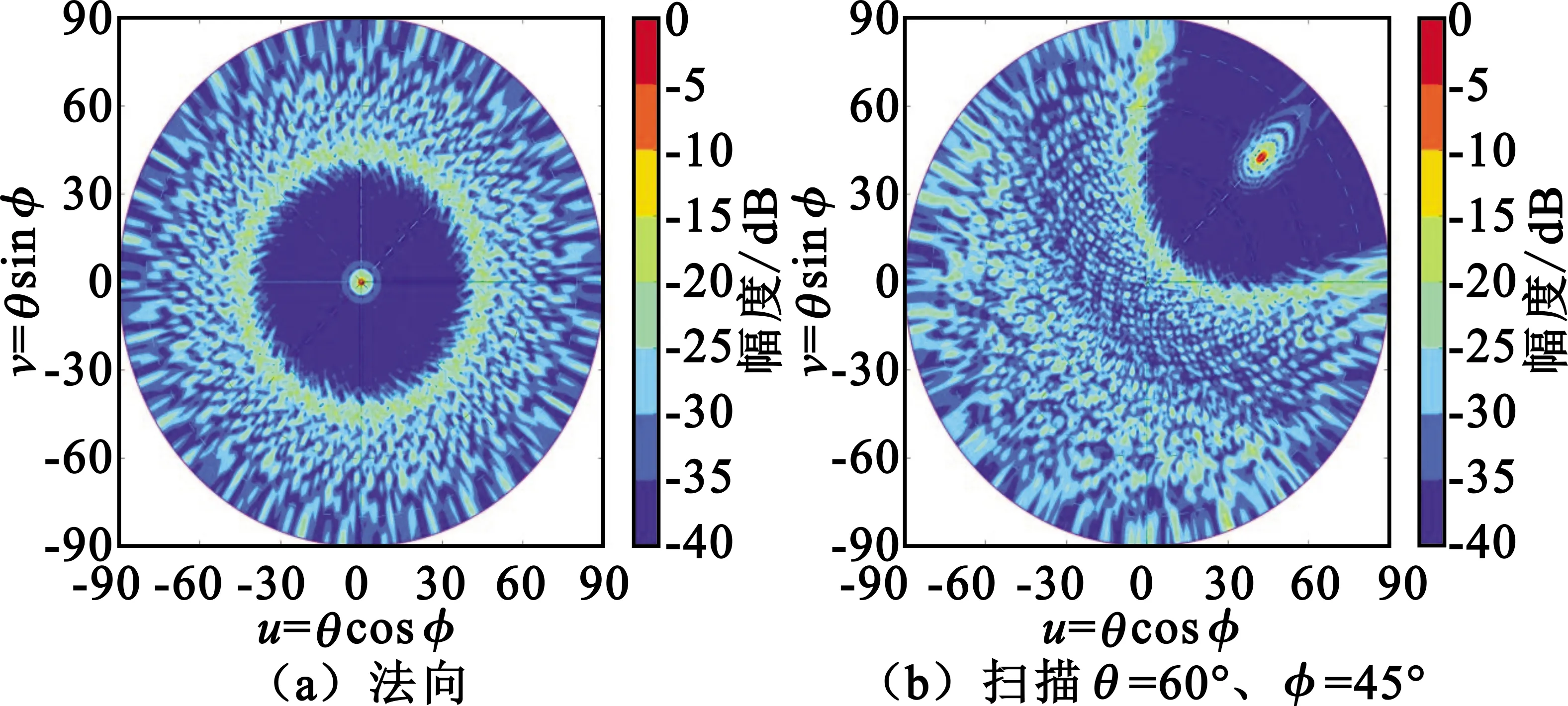
图阵列uv空间归一化方向图

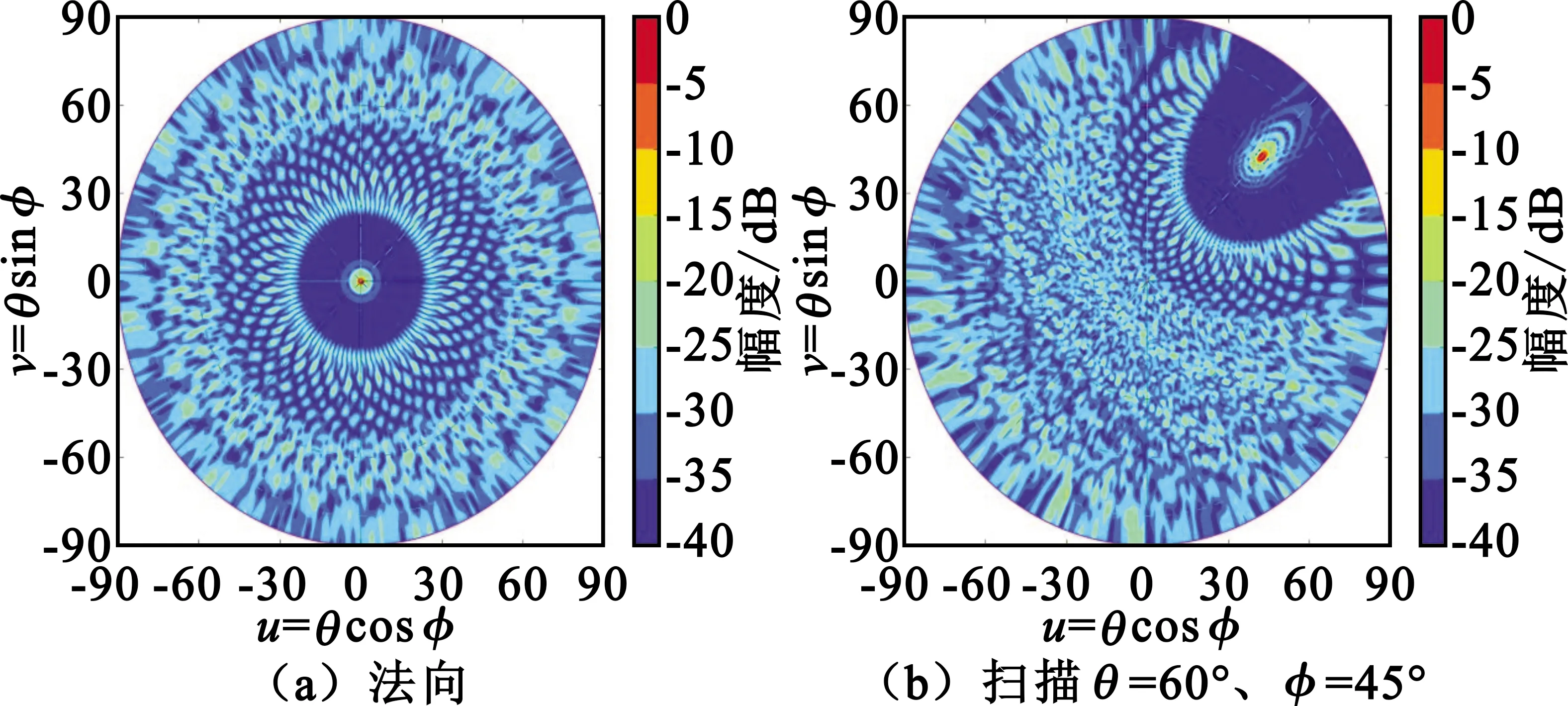
图5 φs=0.617阵列uv空间归一化方向图

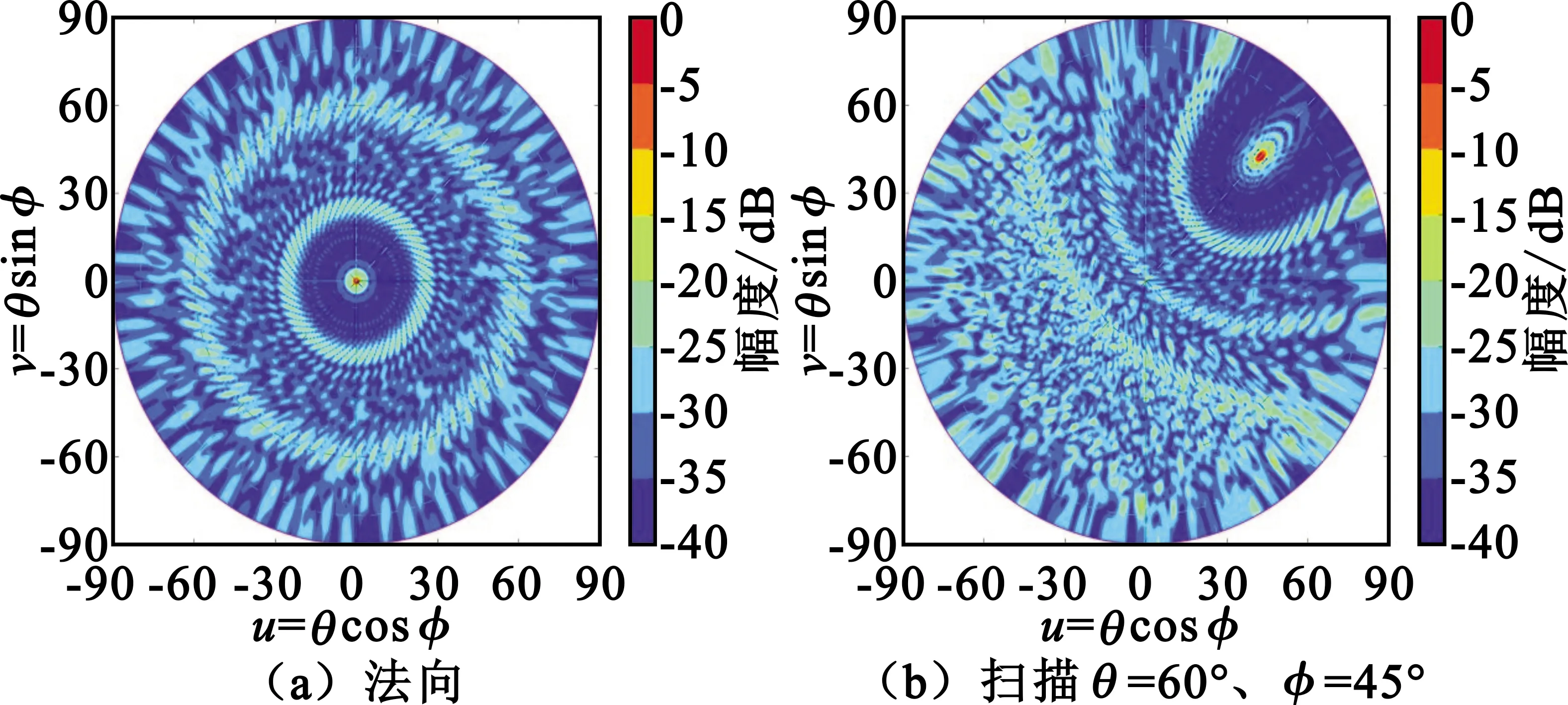
图阵列uv空间归一化方向图

从前面三组方向图可见，副瓣区域能量分配很均匀、无序。三个参数得到的副瓣电平相当，φs=0.617最好。但根据图形特性，黄金分割点云分布最为均匀、紧凑，可以任意等比缩放，较适合于分析相控阵不同间距(即宽频带)的特性。

表2给出了576单元按不同缩放比例的形成阵列的副瓣电平计算结果。阵列半径相差2倍以上，副瓣电平无明显差异，均能达到-16 dB以上，可见这种阵列具有稳定的宽带副瓣特性。

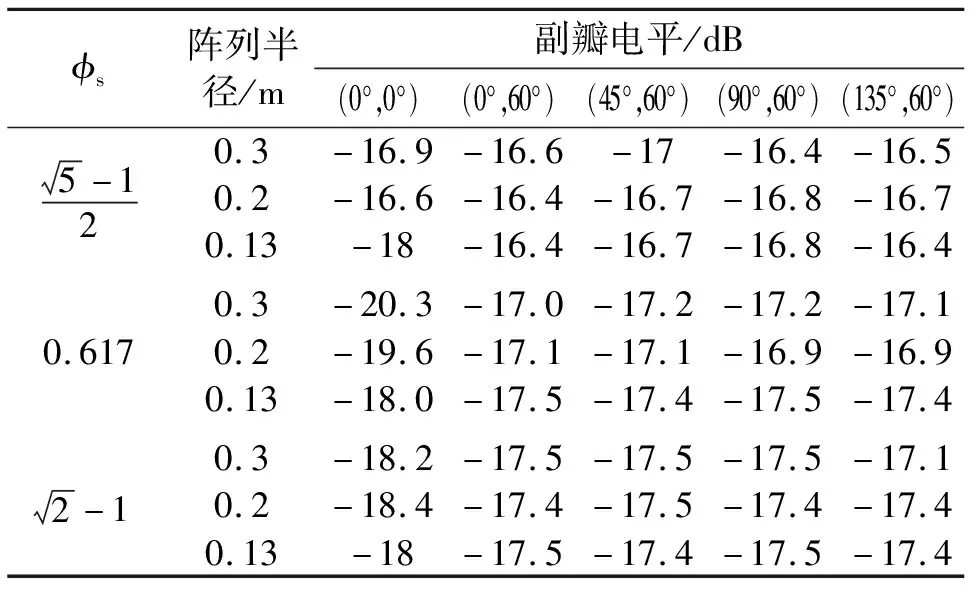
表2 不同φs和半径的网格阵因子副瓣

下面详细分析斐波那契网格阵列的副瓣特性。图7列出了576元阵列在不同方位面的方向图，可看出，最高副瓣为第一副瓣，其电平值约为-17.3 dB，接近等功率分布的圆口径副瓣理论值。而远副瓣分布较为平均，指向为法向时远副瓣电平达到-25 dB，指向大角度(扫描θ=60°、φ=45°)时，远副瓣抬高至约-20 dB。实际远副瓣电平与阵元数量和单元方向图有很大的关系，结合下文的156元阵列分析和电磁场仿真可得出结论，斐波那契网格稀疏阵列的副瓣电平随单元数的增加而改善，天线单元因子及结构件也能显著抑制副瓣。

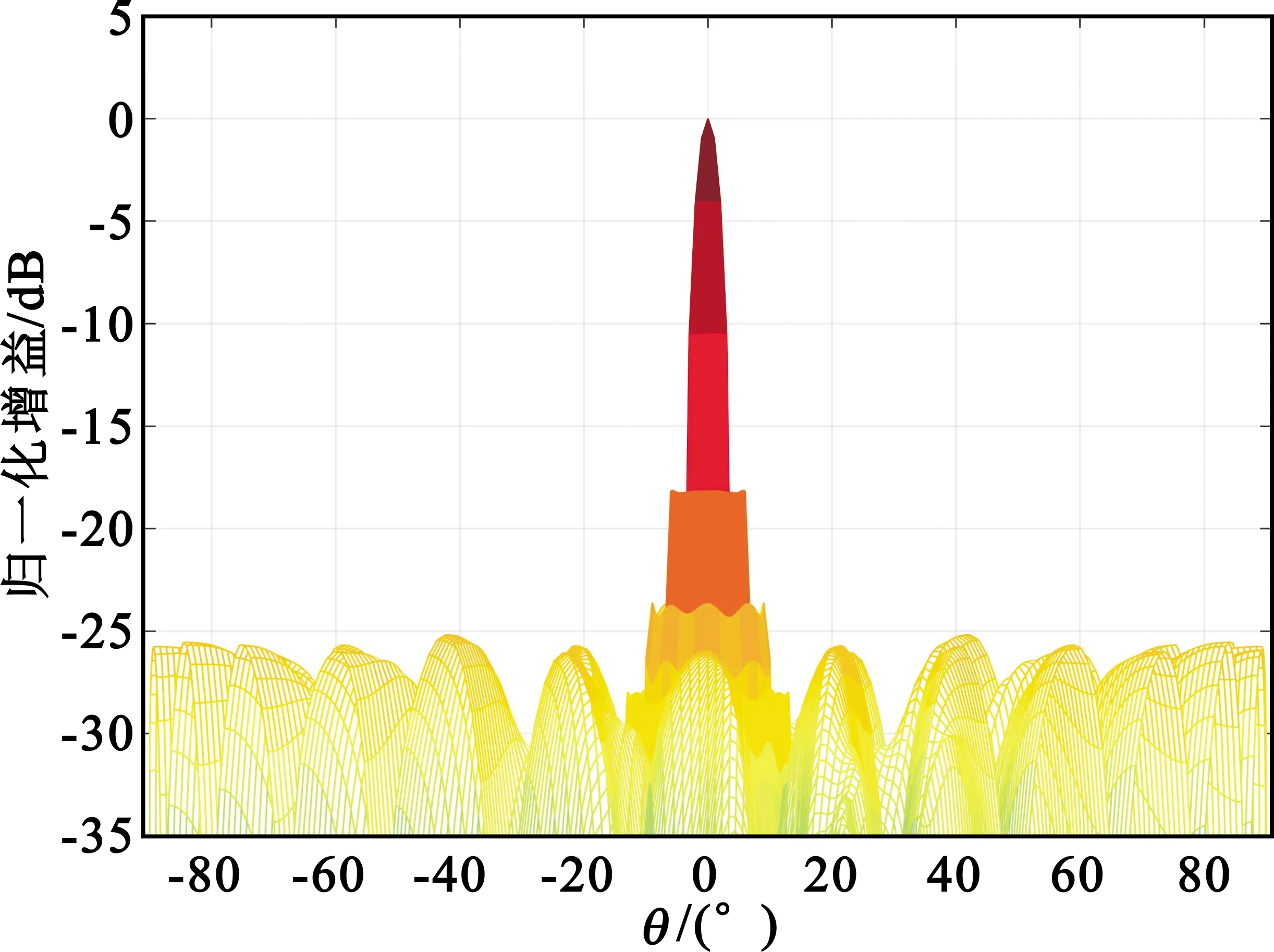
(a)法向

在K/Ka频段通信中，考虑到功放芯片的效率较低并简化控制芯片的设计，一般情况下-20 dB的副瓣电平已完全满足系统需求，所以未对有源相控阵天线的副瓣做进一步的抑制。文献[8]采用密度加权方式进行副瓣抑制，这样造成阵元间距沿径向逐渐扩展，阵列网格不均匀，TR组件芯片与阵元位置及各射频通道的时延难以匹配。

近来低轨卫星宽带网络提出了相控阵天线多波束复用的要求，各波束间需满足频域和空域的隔离度，所以副瓣电平在天线指标体系中的重要性逐步提升。为了克服密度加权方式在K/Ka频段有源相控阵中的不足，本文采用幅度加权抑制副瓣技术。

图8算例中，幅度加权采取从1～576元逐渐衰减地渐变加权，电压幅度归一化加权系数wn=n-0.15，中心和边缘功率加权相差约8 dB，第一副瓣电平可以抑制到-23 dB。当电压幅度归一化加权系数wn=n-0.05，中心和边缘功率加权相差约3 dB，第一副瓣电平可以抑制到-18.5 dB。

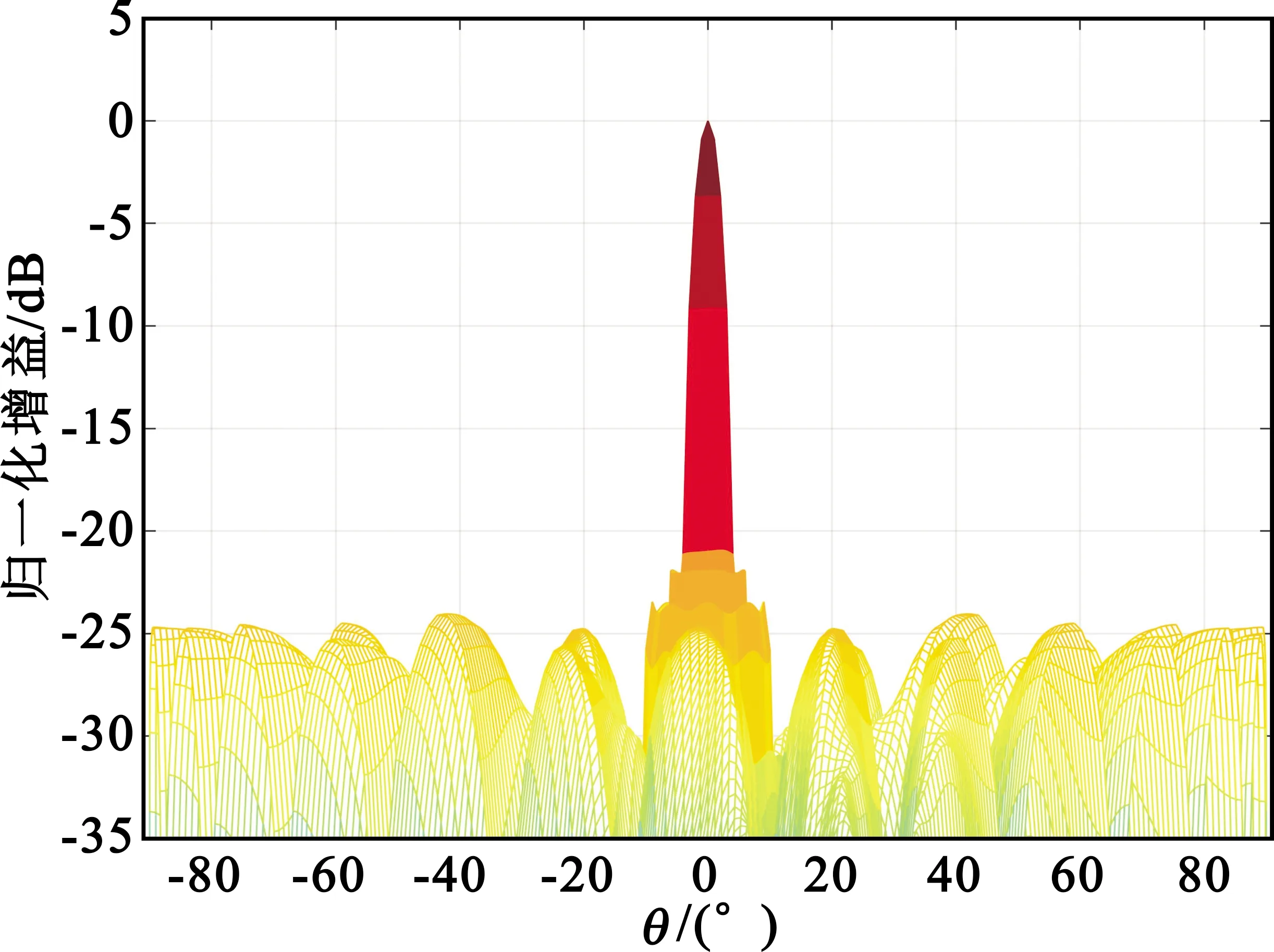
(a)法向

图9算例中，幅度加权采取1～576元1、0.707两档位衰减的阶梯量化加权，电压幅度归一化加权系数wn=1,n∈(1,288),wn=0.707,n∈(289,576)，副瓣电平可以抑制到-19.5 dB。

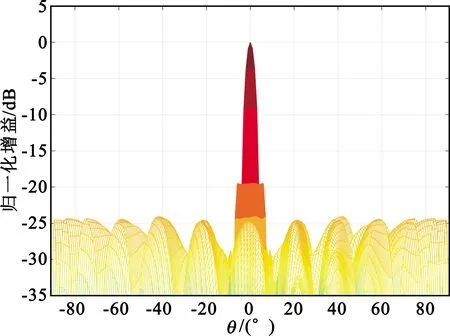
(a)法向

从以上几个算例可看出，采用轻微的幅度加权，即可将第一副瓣电平抑制。工程中，K/Ka频段相控阵控制芯片中配置有高精度数控移相器和衰减器，幅度加权易于实现。

采用幅度加权后，阵列口径增益损失LGain由下式得到：

(9)

式中：N为阵元数。以上几种轻微幅度加权，对天线的增益影响不超过0.2 dB，所以对接收天线品质因数(增益噪声比，G/T值)不会产生明显影响，只是对于发射天线来说要维持等效全向辐射功率(Equivalent Isotropic Radiation Power，EIRP)不变，总的有源功率输出应为等功率加权的N/∑wn2倍。

1.5 156元阵列数值算例

对工作在20 GHz的156元阵进行计算，取不同的φs，并调整缩放比例使156元分布在半径0.15 m的口径中，实现约1.48λ的等效间距；或使其分布在半径0.075 m的口径中，实现约0.7λ的等效间距。

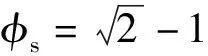
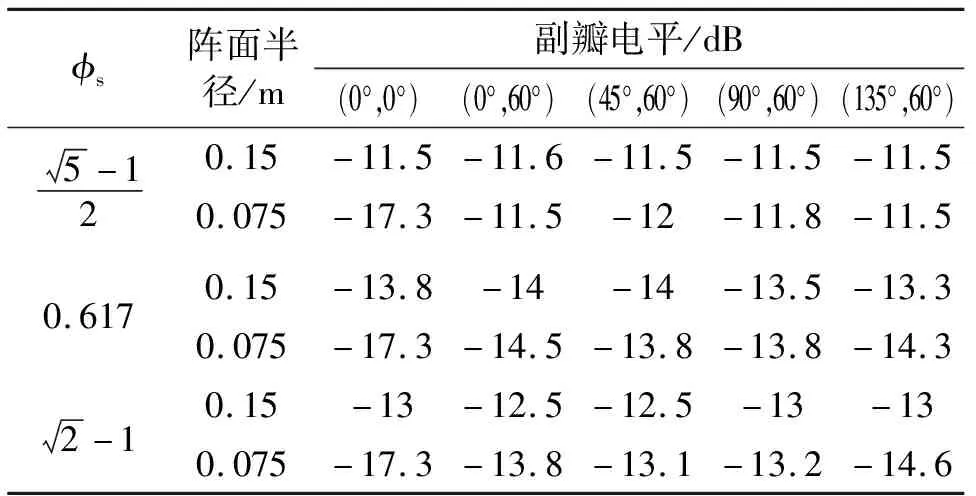
表3 156元阵阵因子副瓣

2 阵面三维电磁场仿真设计

2.1 阵面仿真

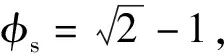
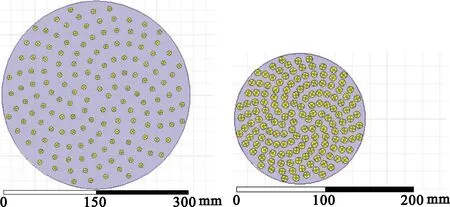
图10 阵面的HFSS仿真模型图

由于阵列的宏观均匀性，各扫描角度均没有显著的副瓣，所以只列出0°方位切面的方向图，见图11、图12、表4、图13、图14和图15所示。

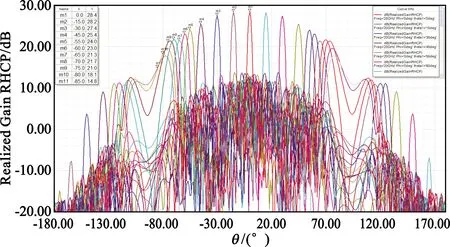
图11 半径0.15 m阵列HFSS仿真方向图(0°方位切面扫描)

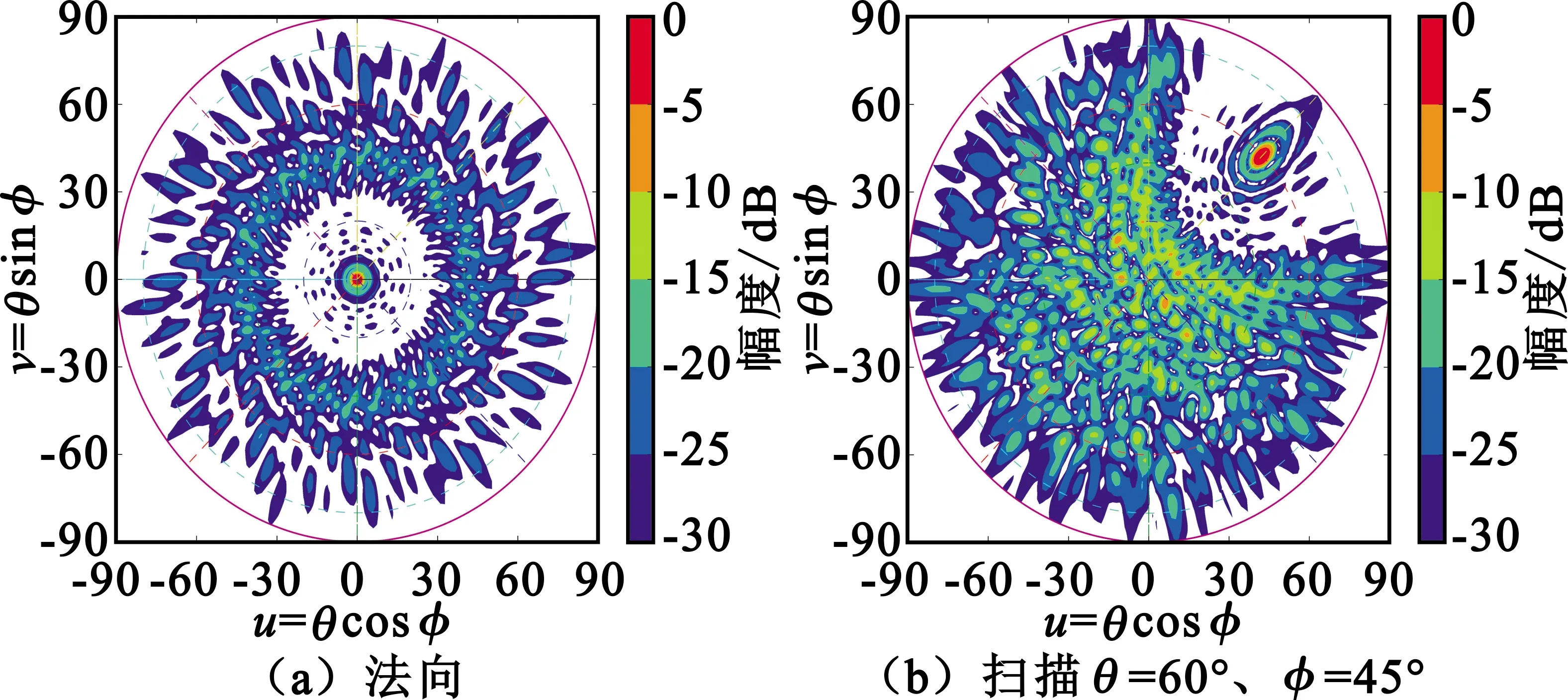
图12 半径0.15 m阵列HFSS仿真uv空间归一化方向图

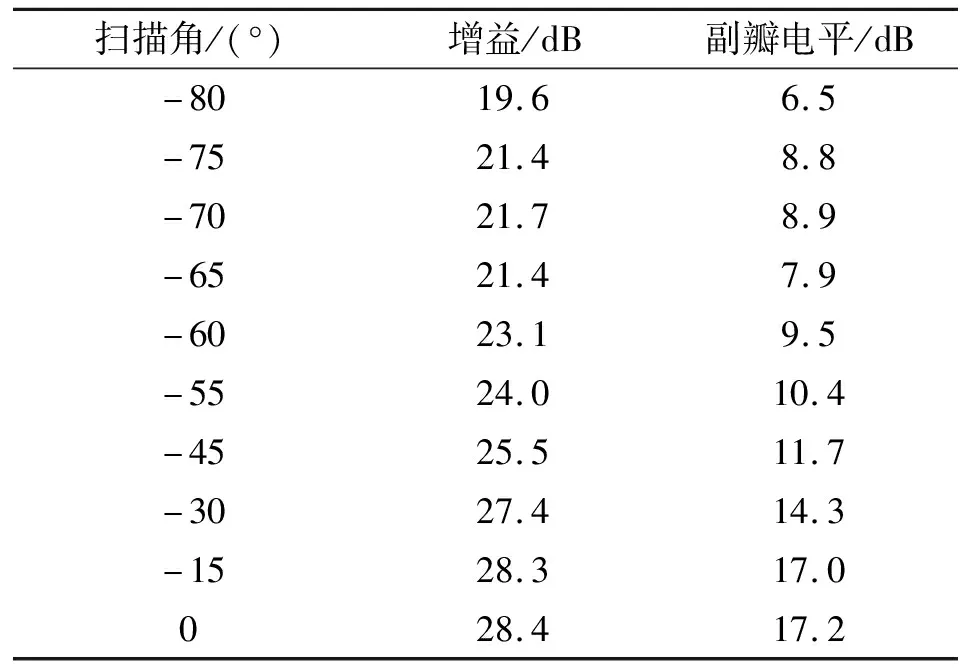
表4 半径0.15 m阵列HFSS仿真结果

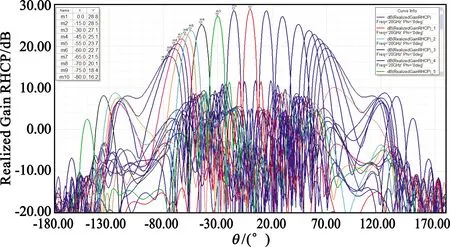
图13 半径0.075 m阵列HFSS仿真方向图(0°方位切面扫描)

图14 半径0.075 m阵列HFSS仿真uv空间归一化方向图

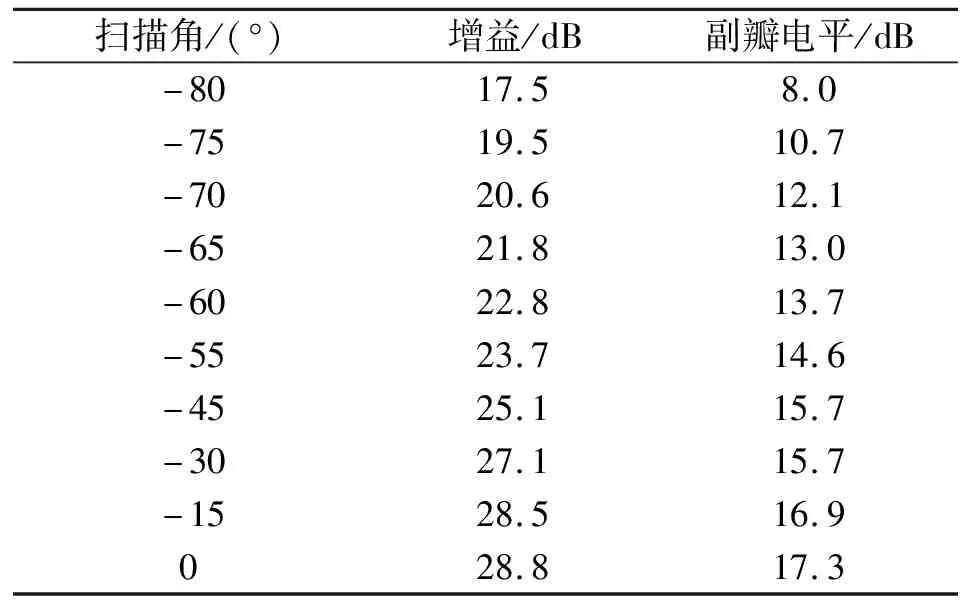
表5 半径0.075 m阵列HFSS仿真结果

根据以上仿真结果可看出，在不同的阵列元间距条件下，扫描方向图呈现不同的特性。半径0.15 m阵列扫描至75°增益可达21.4 dB，而扫描角大于60°时副瓣电平抬高；半径0.075 m阵列扫描至65°增益可达21.8 dB，扫描至75°时副瓣电平仍维持在10.7 dB的水平。进一步分析可知，扫描角超过40°的情况下，最大副瓣均出现在90°以外，属于相控阵扫描特有的后瓣，实际中由于天线安装在面积远大于辐射口径的金属平台中，这种副瓣能被有效抑制。可继续深入优化阵列半径，寻求副瓣的最优结果。

下面分析斐波那契网格大间距稀疏阵列的宽角扫描特性机理。相控阵天线口径增益可表示为

(10)

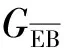
2.2 阵面与TR组件互连设计

针对工作在20 GHz半径为0.15 m的156元阵，按照工程化的要求，对阵元和均匀排布的TR组件进行了接口匹配设计，如图15所示。图中正方形边长为0.5λ，代表一般的谐振式阵列单元占据的面积；将所有单元分成4个象限，用四种颜色区分，是工程中为了避免电路面积过大造成加工成本高、焊接变形等问题的手段；2×2一组的红点表示TR芯片输出至天线单元的接口，间距为20 mm，则集成化的2×2通道TR芯片可利用面积为40 mm×40 mm，给工程化实现提供了相当大的自由度。阵元与邻近的TR通道一一配对形成链表，就可以使用布板软件进行转接层图纸自动化设计。

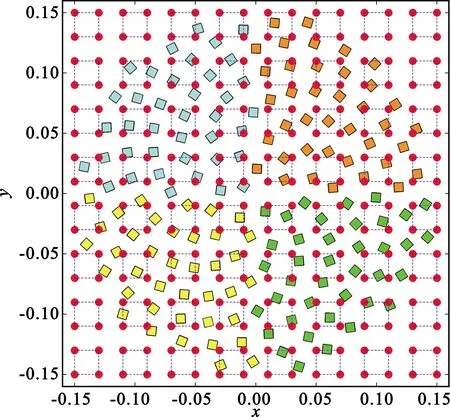
图15 稀疏阵列单元与TR组件接口示意图

3 结束语