一种5G NR系统PSS叠加分段的定时同步算法*

江 航，曹龙汉，张治中，胡昊南

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆通信学院 控制工程重点实验室，重庆 400065)

0 引 言

5G新空口(New Radio，NR)系统是第三代合作伙伴计划(The 3rd Generation Partnership Project，3GPP)组织制定的第五代移动通信技术标准，2019年至今，全球多个国家与地区已经推出了自己的5G服务，5G已经成为主流的移动通信标准[1]。小区搜索是用户端接入网络的第一步，而小区搜索的第一步是实现主同步信号(Primary Synchronization Signal,PSS)的检测与接收，精确检测的性能直接影响到通信链路的建立，5G NR系统对频率偏移有着更为严格的要求[2-3]。因此，对高精度、低复杂度的定时同步算法研究有着极其重要的意义。

长期演进(Long Term Evolution，LTE)系统中典型的定时同步算法有基于PSS信号的自相关算法、基于PSS信号的互相关算法以及基于循环前缀(Cyclic Prefix，CP)的最大似然(Maximum Likelihood，ML)算法[4-6]。5G NR系统相对于LTE系统存在较多的差异，虽然可以直接利用LTE系统中算法，但是由于5G NR系统的特性，导致算法性能不佳。本文针对5G NR系统的特性，对现有定时同步算法进行改进，使其满足5G NR系统的抗频偏和复杂度要求。

针对5G NR系统对频率偏移有着极高的要求，文献[7]提出了一种基于PSS信号的分段互相关算法。该算法通过对接收信号和本地信号进行分段来提高抗频偏性能，但在信噪比相同的情况下，分段数的增加会影响同步性能,分段算法仍然存在计算量大的缺点。本文利用分段互相关算法的抗频偏优势，提出了一种基于分段互相关算法的改进算法，对本地信号进行对应叠加成一组本地信号，再与接收信号做分段互相关运算，检测峰值，获得粗同步点和子载波配置参数μ，最后取粗同步点降采样前后若干点组成序列与本地信号做互相关，获取精同步点与小区组内ID。该算法可提升定时同步检测的抗频偏性能，且有效降低实现复杂度。

1 主同步信号

5G NR系统中的物理小区ID数与LTE存在差异，由504个增加到1 008个，分为336组，每组3个。

(1)

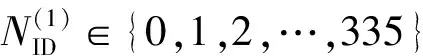
主同步信号没有继续采用LTE中Zadoff-Chu序列，改用了长度为127的二进制相移键控(Binary Phase Shift Keying，BPSK)调制的M序列，该序列具有良好的自相关特性和较好的互相关特性。

主同步信号生成方式如下：

(2)

式中：x(6)=1，x(5)=1，x(4)=1，x(3)=0，x(2)=1，x(1)=1，x(0)=0。

相对于LTE系统，5G NR系统中的PSS、辅同步信号(Secondary Synchronization Signal，SSS)、物理广播信道(Physical Broadcast Channel，PBCH)以及解调参考信号(Demodulated Reference Signal,DM-RS)映射到一个SSB(SS/PBCH)块，映射关系如图1所示。SSB由频域中的20个物理资源块(Physical Resource Blocks，PRB)和时域中的4个正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)符号组成，如图1所示，PSS位于符号0的56～182子载波；PBCH位于符号1、3以及符号2，其中符号1、3上占用所有子载波，符号2上占用0～47、192～239子载波；SSS位于符号2的中间56～182子载波；DM-RS位于符号1、2以及符号3，以步长为4间隔放置，每个符号上60个。

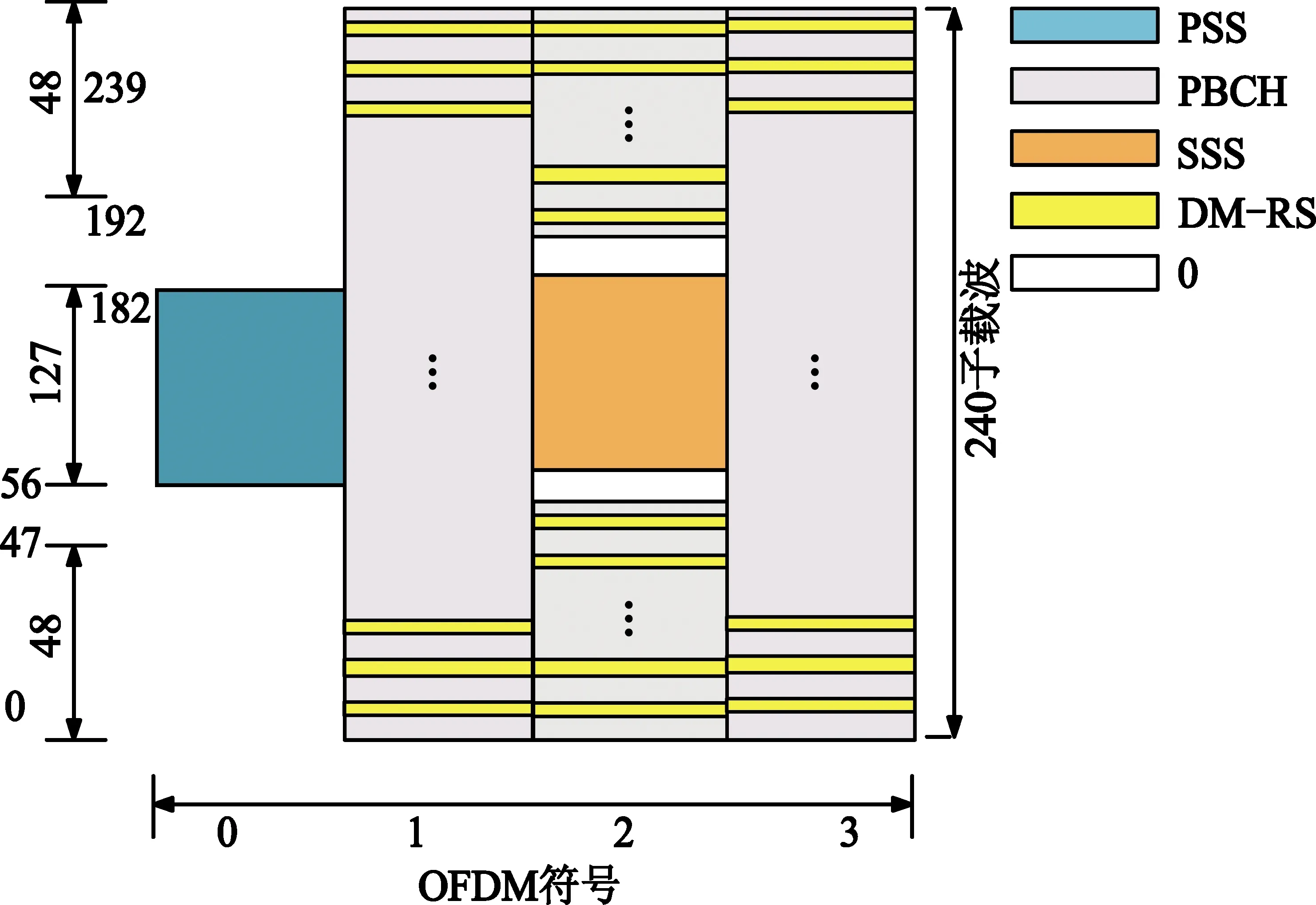
图1 SSB块映射关系

5G帧结构包含10个子帧，相对于LTE，5G定义了灵活的时隙架构，每个子帧有包含干个时隙，如表1所示,每个子帧时隙数、子载波间隔与子载波配置参数μ值密切相关。本文取μ=0，则子载波间隔为15 kHz，每个子帧包含1个时隙，每个时隙包含14个OFDM符号，此时SSB块在无线帧的位置如图2所示。

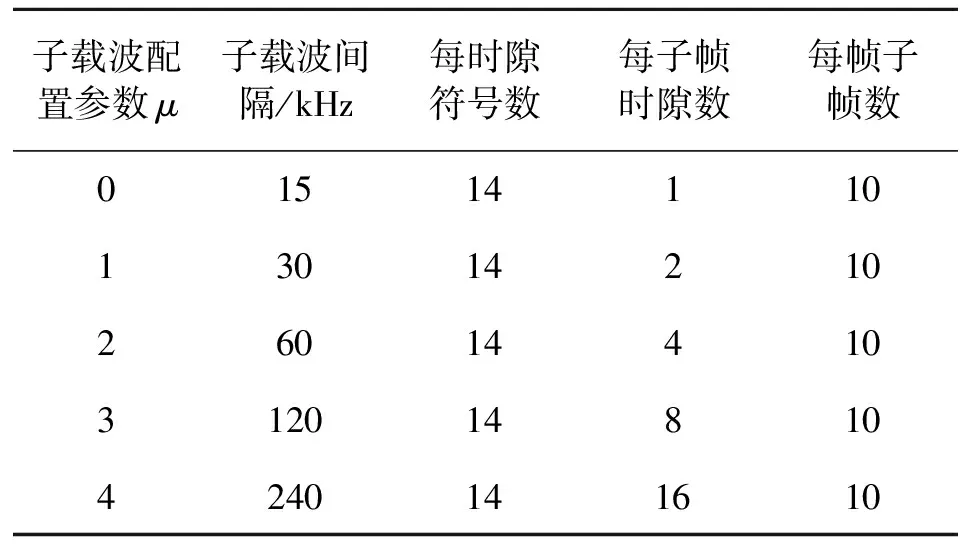
表1 子载波配置参数μ与各变量之间的关系

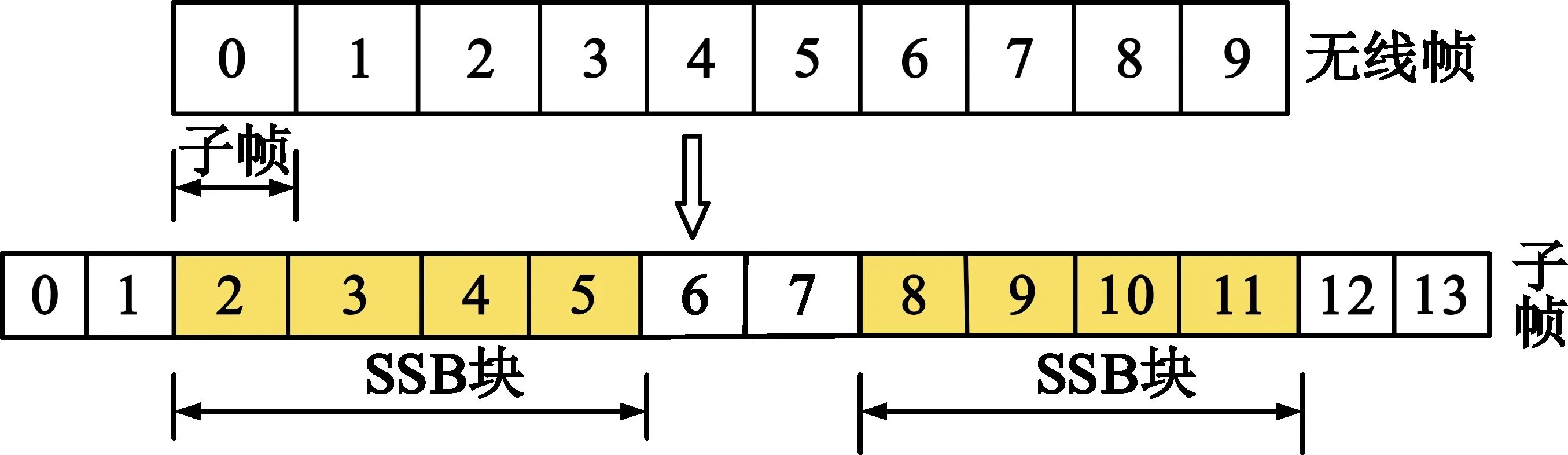
图2 SSB在无线帧中的时域位置

2 PSS同步算法分析与改进

2.1 传统互相关同步算法

PSS具有良好的互相关特性，通过接收信号直接与本地PSS信号直接互相关实现定时同步[7-8]，检测相关峰值，其度量函数为

(3)

式中：q={0,1,2}，PSS(q,μ)(i)为本地生成的子载波控制参数为μ时第q组PSS信号，r(n)为接收信号。

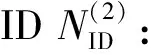
(4)

2.2 分段相关同步算法

在5G NR系统中不可避免地会产生载波偏差等问题，传统互相关算法不能有效解决频率偏移问题。为此，文献[9]提出了一种将PSS信号分段相关的同步算法。该算法通过分段，缩短了相关运算长度，减小了频偏的累计，增强了算法的抗频偏的性能。其度量函数为

(5)

式中：μ={0,1,2,3,4}，M为分段数，L为各段长度。

2.3 定时同步算法的改进与分析

为了降低本地互相关算法的复杂度，提高算法的抗频偏性能，本文针对分段算法进行改进，提出了本地PSS序列对应叠加与分段相关相结合的算法。定时同步改进算法的整体设计流程如图3所示。

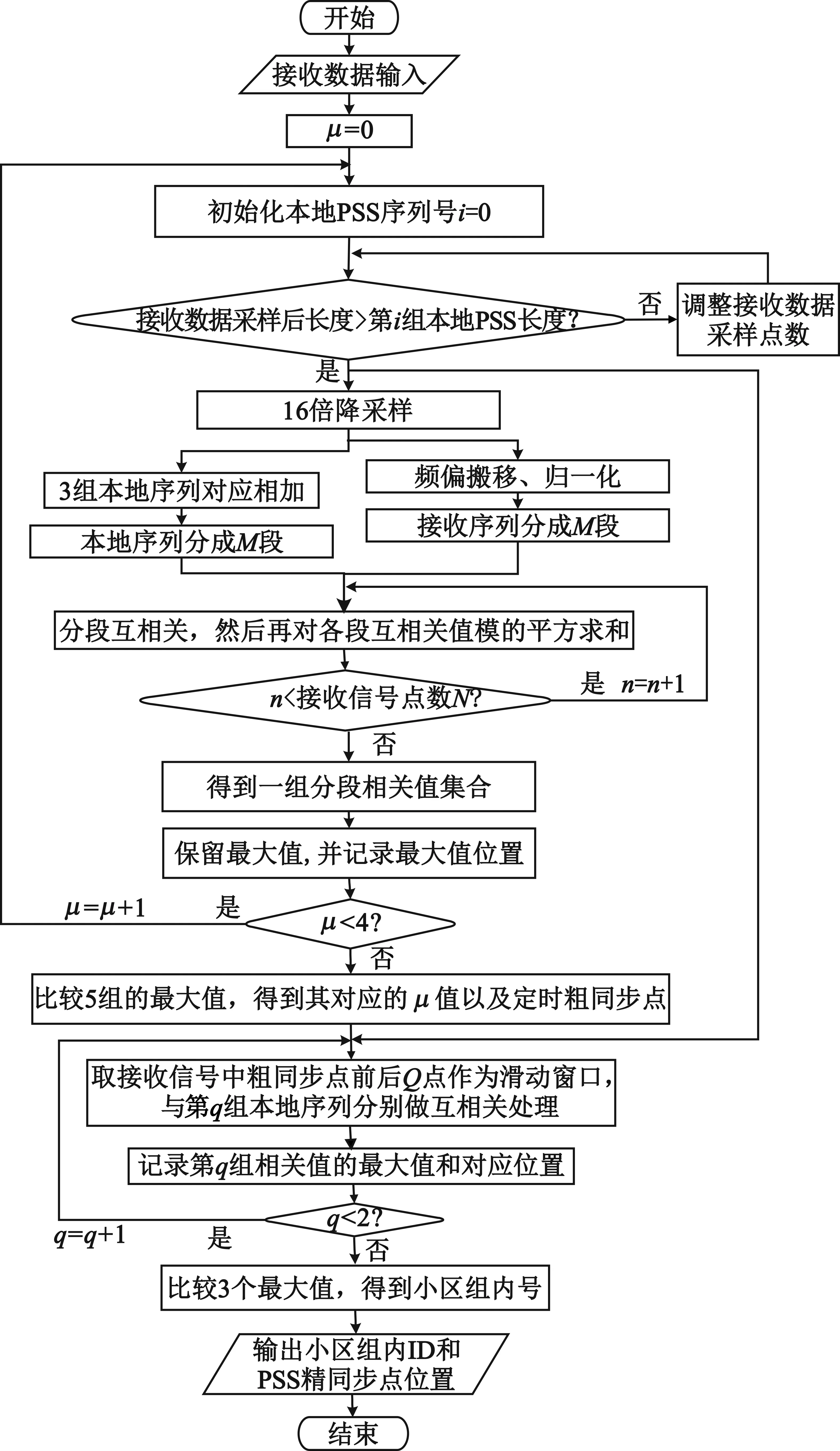
图3 定时同步改进算法设计流程图

首先，以16倍的采样率对接收信号与本地PSS信号进行降采样，以减少运算点数，降低运算量。根据互相关运算性质，A与(B+C)做互相关运算的值等于A与B、A与C做互相关运算的值之和[10]：

A×(B+C)=A×B+A×C。

(6)

M序列具有良好的自相关和互相关性，利用互相关特性，将本地三组PSS信号对应叠加，然后与接收到的PSS信号进行互相关运算。如图4所示，检测到的峰值点坐标为1 125，传统互相关算法得到峰值点坐标为1 125，峰值点坐标完全一致，只需要进行一次互相关运算，极大地减少了计算量。

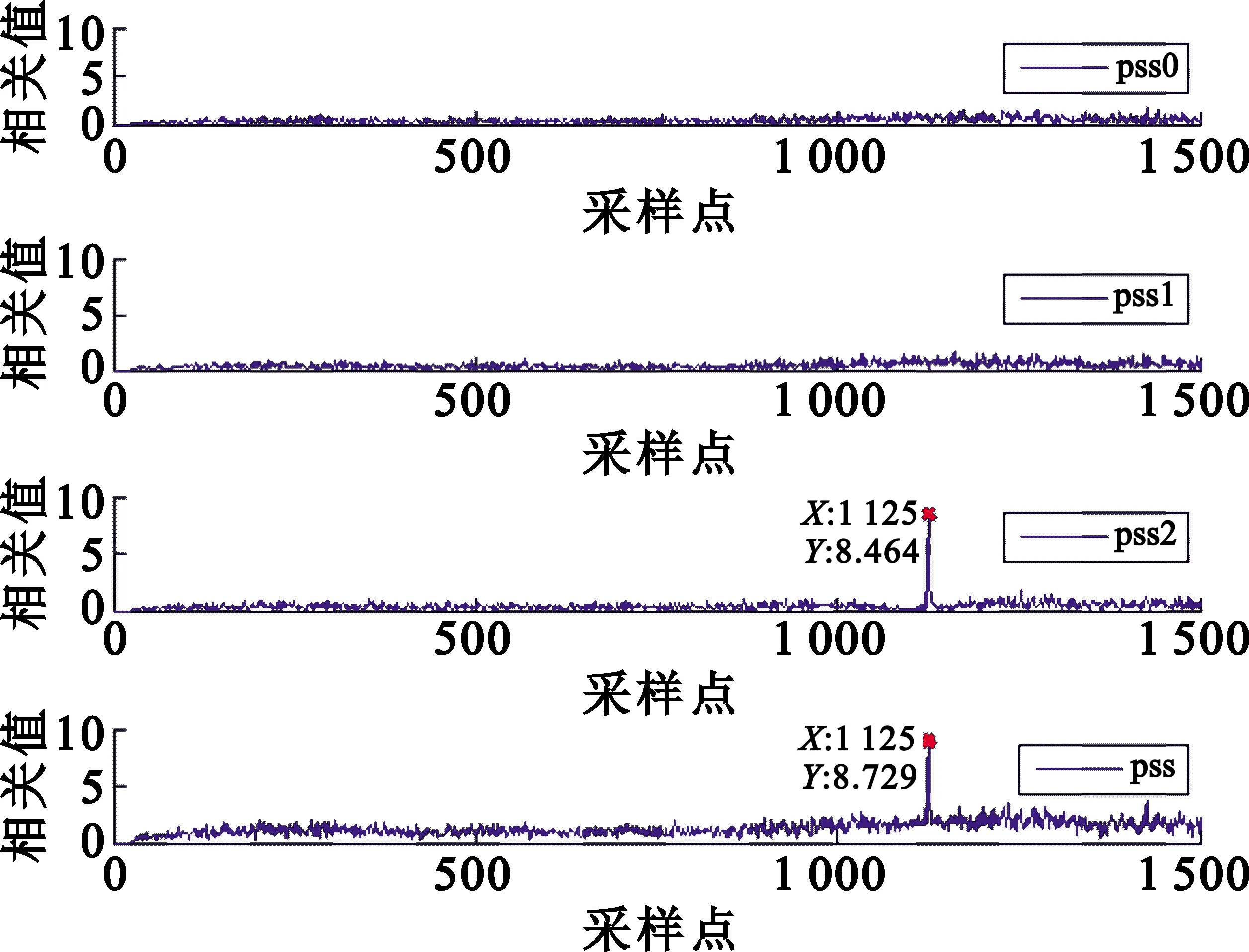
图4 接收信号与本地PSS信号的相关性

降采样后的三组本地PSS信号分别用PSS(0,μ)(i)、PSS(1,μ)(i)和PSS(2,μ)(i)表示。对三组本地PSS信号进行对应叠加处理，公式如下：

PSSμ(i)=PSS(0,μ)(i)+PSS(1,μ)(i)+PSS(2,μ)(i)。

(7)

对本地PSS信号完成对应叠加后，将对应叠加后的本地信号PSSμ(i)与接收信号r(n)均分成M段进行互相关，然后再对各段互相关值求模的平方和。将三组本地PSS信号相加为一组做滑动相关，算法表达式如下：

(8)

式中：M为分段数，且L为每段长度。

对各段滑动窗内的信号能量进行归一化，使得判决函数不受接收信号强弱的影响。表达式如下：

(9)

(10)

5G NR系统中μ={0,1,2,3,4}，因此需要进行5次互相关，得到5个最大峰值集合，进而比较可确定最大值对应的μ值和粗同步点。表达式如下：

(d,μ)=argmax{|Cμ(n)|}。

(11)

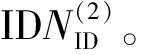
(12)

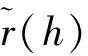
(13)

3 仿真与分析

为了验证算法的性能，将本文提出的算法与传统互相关算法、分段互相关算法作比较，在不同影响条件下利用Matlab软件进行仿真，仿真参数如表2所示。

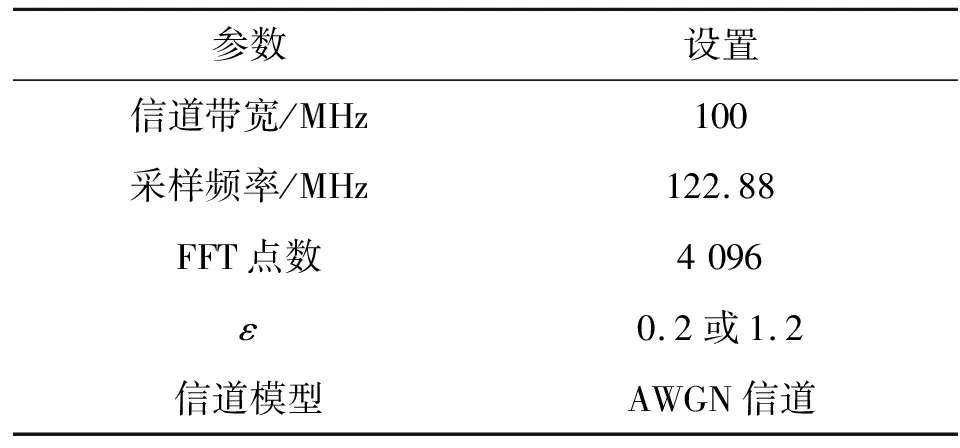
表2 仿真参数表

在理想无噪声的加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下，ε=Δf/fsc为归一化频偏，Δf为发送和接收之间频偏值，fsc为子载波间隔，本文取子载波控制参数μ=1，则此时子载波间隔fsc=30 kHz。图5和图6分别是ε=0.2和ε=1.2时传统互相关算法的相关峰值图，图7为M=4且ε=1.2时本文改进算法的相关峰值图。由图5和图6可知，传统算法在小频偏时检测性能较为优秀，峰值明显，但在大频偏时峰值不明显，性能较差。对比图6和图7可以看出改进算法在大频偏时依然具有明显的峰值。

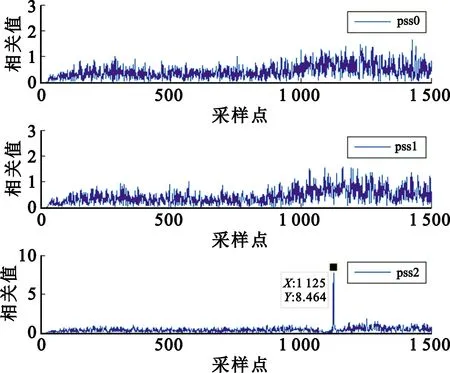
图5 ε=0.2时传统互相关算法峰值图

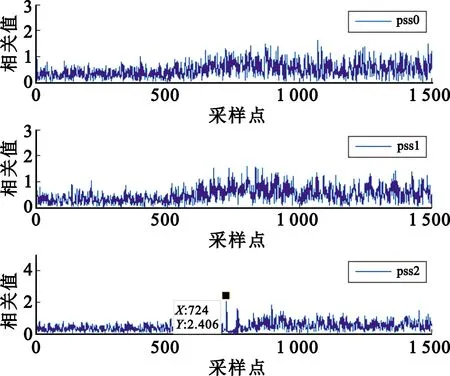
图6 ε=1.2时传统互相关算法峰值图

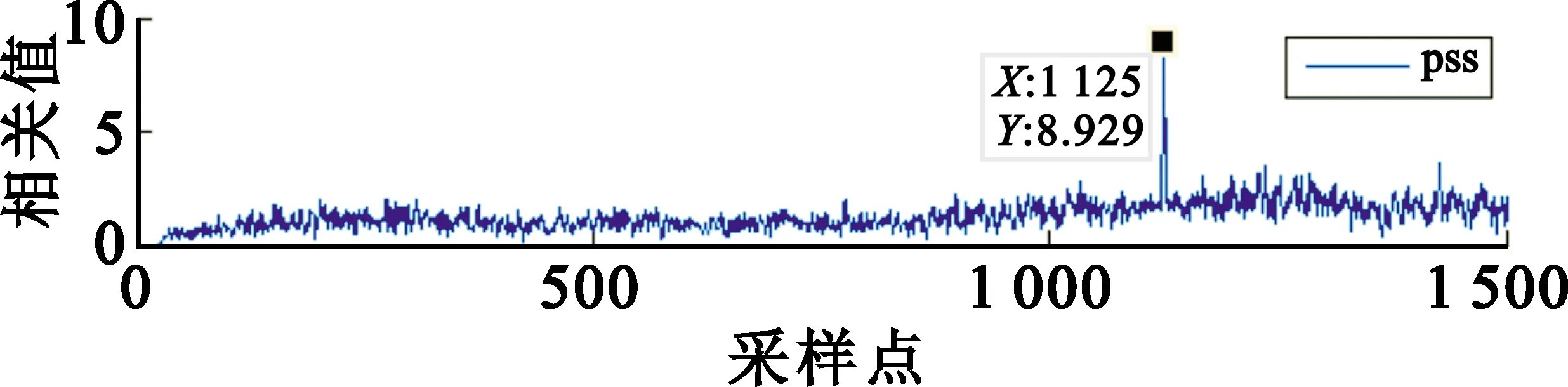
图7 ε=1.2时改进算法峰值图

经过上述计算得到粗同步点的位置为1 125，对应于降采样前的位置为17 985，在此截取前后共Q点长度，由图8得知，当Q=64时检测正确率即可达到1。

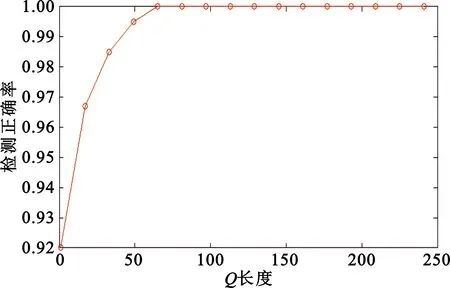
图8 不同Q值主同步信号的精同步点检测正确率

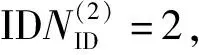
图9 精同步点定时位置

图10(a)和图10(b)分别表示ε=0.2和时ε=1.2不同算法的检测概率。由图可知，无论在ε=0.2还是ε=1.2，本文改进算法性能最为优秀。分段数也会影响检测概率，当分段数M=4时，在低信噪比下的检测性能高于分段数M=8时，故本文改进算法选用M=4时，用于计算粗同步点与精同步点。图10(b)表示出三种算法在高频偏值的情况下，低信噪比时算法性能极为糟糕，随着信噪比的增加，检测性能均得到有效改善，其中本文改进算法性能表现最为优秀。

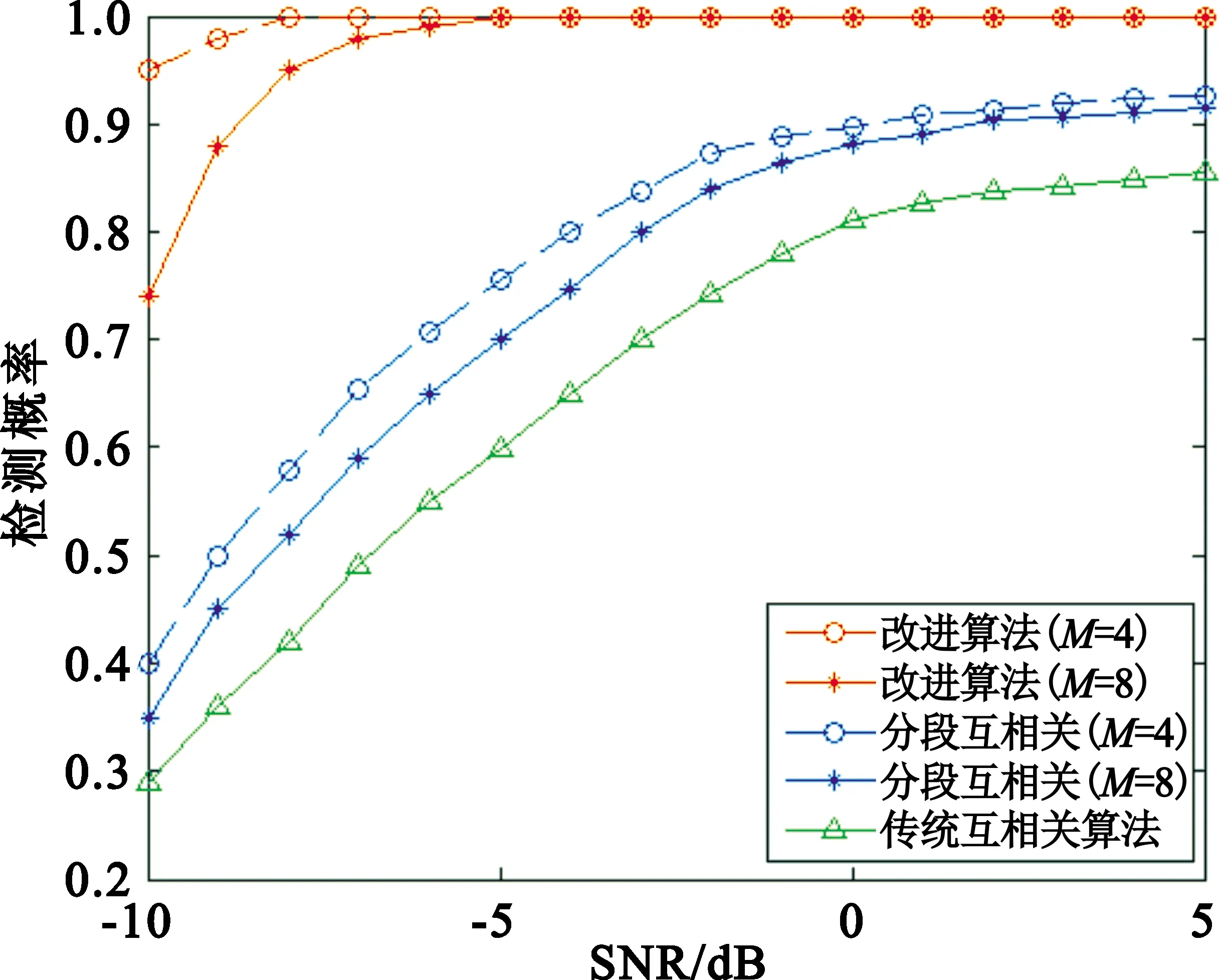
(a)ε=0.2

本文通过对比15组相关序列的峰值大小，从而确定μ值、小区组内ID和定时同步点。在同步过程中，以μ=1、子载波间隔30 kHz、采样频率122.88 MHz为例分析比对不同算法的计算复杂度。选取降采样后半帧38 400点长度的数据进行对比分析。传统互相关算法的复数乘法和复数加法运算量分别为38 400×256×3+4 096×64=2 9753 344和38 400×255×3+4 096×63=29 634 048；分段互相关算法(M=4)的复数乘法和复数加法运算量分别为29 753 344和22 030 848；本文改进算法(M=4)复数乘法和复数加法运算量分别为38 400×64×4+64×4 096×3=10 092 544和38 400×63×3+4 096×63×3+38 400×3=8 146 944。详细的运算复杂度数据如表2所示。由表可知，改进方案复数乘法和复数加法的运算量比传统互相关算法减少了66.08%和72.5%。从整体的运算量可得出，本文算法相比较分段互相关算法，运算量减少了64.78%。

表3 运算复杂度分析比对

4 结 论

传统PSS同步算法性能难以满足5G NR系统的要求，本文根据PSS序列的特性，对PSS定时同步算法进行改进，提出分段相关与对应叠加的联合检测算法，并设计了详细的定时同步检测方案。其中，改进算法的计算复杂度相对传统互相关算法减少了大约66%。仿真结果表明，在AWGN信道中，相同信噪比情况下，改进算法抗频偏性能始终优于传统同步算法；低信噪比情况下，改进算法相比较传统互相关算法检测概率提升明显，且计算量小，抗频偏性能强，易于实现。目前该算法已应用于重庆市创新重大主题专项项目“5G路测仪表”，取得了良好的测试效果。