基于角度重构和差分飞行时间的室外多站定位*

罗 斌，蒋 青，吴啟弘，余箭飞，陈 希

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

目前，室外非视距(Non-line of Sight,NLOS)定位技术主要可以分为基于散射体相关信息的非直达波定位方法和基于不等式约束和统计模型的非直达波定位方法。基于散射体相关信息的非直达波定位方法又可以分为两类[1]。一类是基于散射传播模型的室外NLOS定位方式，通过对散射体模型的研究从而获得各种场景下的参数统计分布来完成对移动台的定位[2]。在散射体传播模型中通常假设散射体按照某种特定的方式分布，例如在移动台周围均匀分布或者随机分布、在移动台与基站之间按某种方式分布等。例如文献[3]利用了多路径散射模型来考虑NLOS传播对定位的影响，利用模型推导出到达时间(Time of Arrive,TOA)的概率密度分布函数(Probability Distribution Function,PDF)，将最大似然期望极大化并且将贝叶斯估计应用于每个基站(Base Station,BS)处的多路径TOA测量中，从而估计移动台(Mobile Station,MS)与BS之间的直视(Line of Sight,LOS)距离。但其统计误差较大，定位精度不高。文献[4]提出了一种应用于蜂窝网的椭圆散射体模型，该模型中散射体均匀分布在以基站和移动台为焦点的椭圆上。但此方法对模型依赖特别大，与实际环境有很大差别。另一类是基于散射体几何位置关系的室外NLOS定位方式，其原理是将定位误差转化为测量因素，当测量因素较准确时，定位性能也大幅度提高。如文献[5]提出几何建模将无线传播信道中发射机、散射体和接收机之间的空间几何关系理想化得到各种信道衰落指标的封闭公式，然后进行定位，但理想化后的几何模型与实际定位环境有一定的差别。文献[6]提出了一种改进的加权定位算法，该算法利用了单元布局的几何特征和三个基站的TOA距离测量值，但其方法过于理想。

基于不等式约束和统计的非直达波定位方法主要使用在没有LOS参考点或没有NLOS误差先验知识的状态下，将目标或者散射体等限制在一定的区域，再根据约束关系得到相应的表达式，即转化为一种数学规划问题，然后结合其他信息进行目标位置求解，如约束最小二乘定位算法，其他约束方法还包括半正定规划法、线性规划法、内点法等[7]。文献[8]中提到的方法则是将Chan的两次加权最小二乘算法(Twice Weighted Least Squares, TWLS)应用到TOA定位中，并对其第一步改进，引入了一些正性约束。基于约束优化的方法由于要进行大量搜索，对搜索算法的收敛速度要求较高。此类算法运算量相对较大，而且约束区间和约束条件的选择也会影响定位精度。

本文提出了一种基于到达角(Angle of Arrival,AOA)重构和差分飞行时间(Time of Flight,TOF)的室外NLOS环境下多站定位方法，其探测信号反射的电磁波，利用多径信号的差分TOF，减轻收发不同步带来的相位误差影响；多站联合估计，使定位精度更高。该方法主要在基站侧对散射体的到达角进行重构从而构建出目标的到达角，再根据几何位置关系和差分TOF建立定位方程。将模型中散射体的分布特性应用到定位当中，增加了信息量。然后将定位问题转化为最小二乘问题进行求解，再利用列文伯格-马奈尔特法(Levenberg-Marquardt,LM)算法初步求出目标与各基站之间的距离。最后用泰勒级数展开法并联合多个基站进行多边定位得到最终的定位结果。本文方法利用NLOS多径信号定位，越过了传统的NLOS抑制方式进行定位，收敛速度快，定位精度较高。

1 定位模型描述与定位方程构建

1.1 定位模型

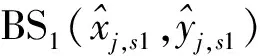
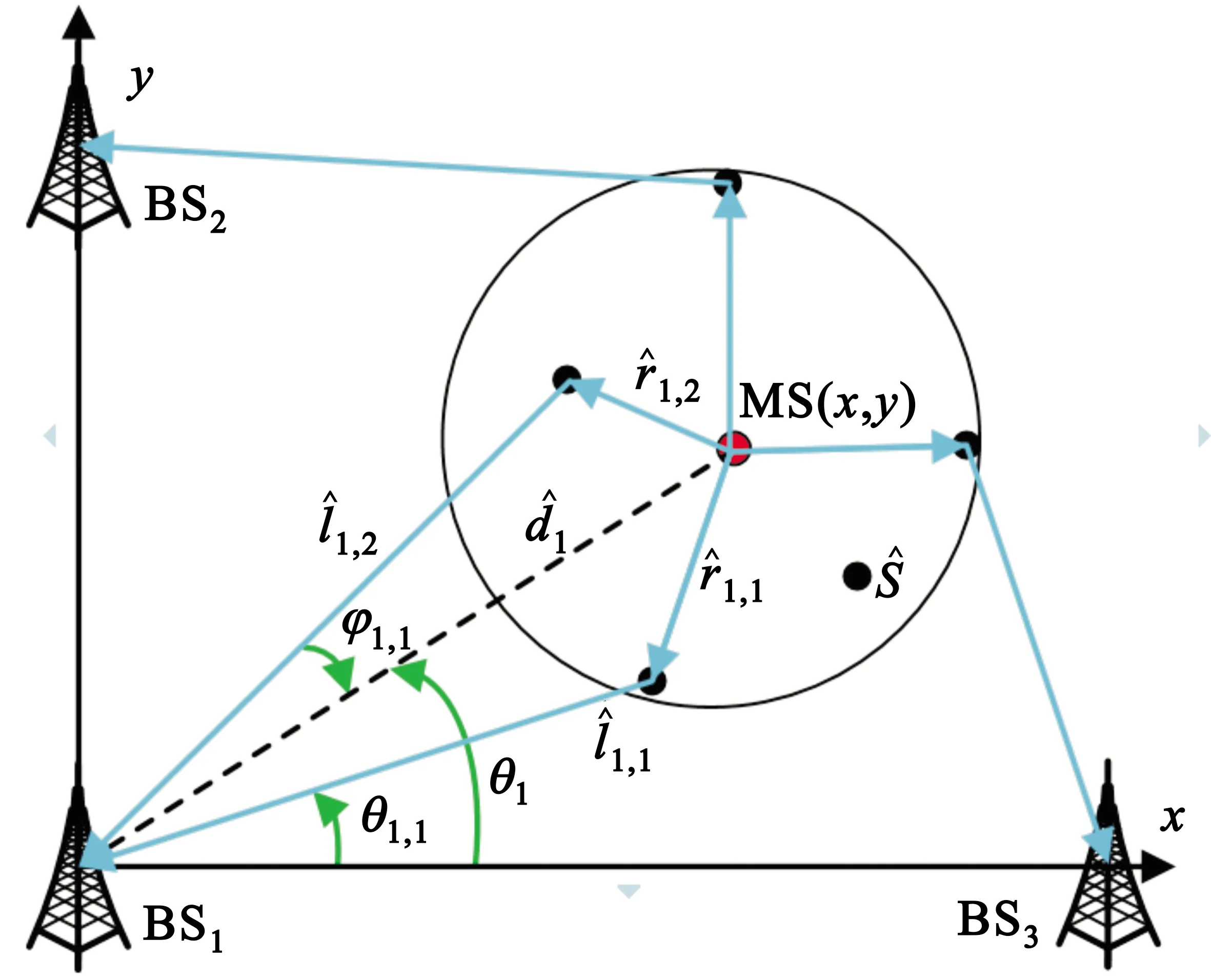
图1 多基站NLOS环境下散射体模型

1.2 角度重构与几何推导

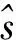
(1)

(2)

由于散射体在DOS和ROS模型中都服从均匀分布，所以散射体出现在MS两侧的概率是相等的，但在实际情况中会出现散射体分布不均匀甚至散射体只分布在MS一侧的情况，此时用单个基站进行角度重构可能会出现重构的角度误差很大的情况。由于所有基站都同时出现单边反射的概率非常低，因此本文提出多个基站参与定位，每次使用重构角度有效的基站进行定位。所以多个基站参与定位且当散射体数量足够时，由角度均值重构法可以得到MS的AOA，如以下方程所示:

(3)

式中：θj,i为散射体到BS的AOA。从图1可以看出，对每个BS来说第i条多径信号有

φj,i=|θj-θj,i|。

(4)

式中：φj,i为BS到MS方向与BS到散射体方向的夹角。根据余弦定理有

(5)

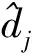
1.3 定位方程构建

由于室外数据采集时，让各基站保持同步非常困难，因此本文使用了CSI信道仿真来模拟室外各个场景的信号传播特性，其中包含了距离、散射、衰落等对信号的影响，并生成包含角度、时延、相位等特性的NLOS信号数据。信道频率响应(Channel Frequency Response,CFR)记为[11]

(6)

式中：A和t分别为反射路径信号的幅度和TOF，基站能接收到的多径信号数量为n，f表示载波频率。假设BS使用N个阵元的线性阵列接收信号，如2行8列加上双极化组成的32个天线。采用正交频分复用调制方式，子载波数为M，则所有天线的子载波CFR矩阵为

Z=[h1,1,…,h1,M,…hN,1,…hN,M]。

(7)

(8)

式中：c为电磁波在真空中的传播速度，τi为估计误差，t(φCFO)为相位误差引起的公共误差。基准路径的TOF可以表示为

(9)

则第i条路径与基准路径的差分TOF可由式(8)和式(9)作差得到:

(10)

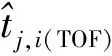
(11)

联立式(5)和式(11)得到

(12)

式中：对于每个BS，未知量有n+3个，总的方程数有2n-1个，方程组为超定方程。由于在NLOS环境中，AOA和TOF测量存在误差，因此可以将方程组求解转化为最优问题求解：

(13)

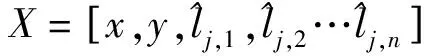
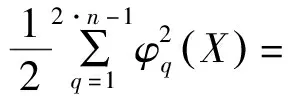
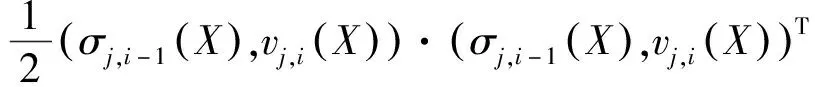
(14)

2 可行域分析和目标位置求解

2.1 目标可行域分析

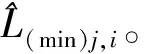
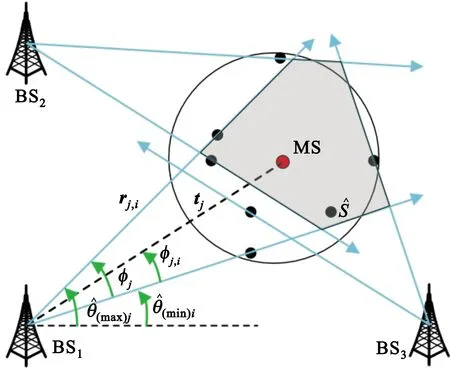
图2 目标可行域

(15)

tj与rj,1和rj,n形成的夹角分别记为φj,1和φj,n，则有

(16)

(17)

目标可行域的数学表达式记为g(X),则

(18)

结合目标可行域可以将定位问题转化为最小二乘问题：

(19)

2.2 目标初始位置估计和多站联合定位

高斯牛顿法、LM算法[13]是求解最小二乘问题的经典优化算法，然而高斯牛顿法存在收敛困难的问题，因此本文选择用LM算法进行MS位置初始求解。LM算法利用迭代可求出最优解：

Xk+1=Xk+λkδk。

(20)

式中：λk为第k次搜索步长，δk为目标函数的下降方向，可以表示为

δ=-(JTJ+εI)-1JTρ。

(21)

(22)

结合先验知识将式(22)简化,使其只具有一个正确的解，以消除可行域中位置模糊度，即

(23)

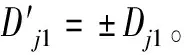
(24)

假定(x0,y0)的初值为(x00,y00)，通过Taylor级数展开可以将式(24)线性化得

(25)

式中：

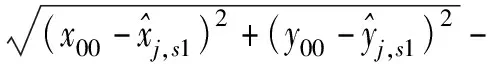
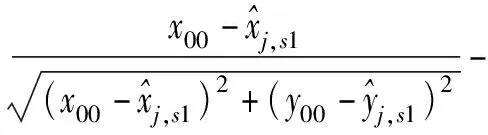
δx=x0-x00，

δy=y0-y00。

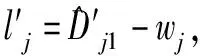
(26)

式中：

则式(26)可写成

(27)

剩余误差平方和为VTV，构造误差函数：

(28)

当VTV最小时，可以得到估计量的最优解。因此对式(28)求导并令其值为零得

(29)

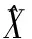
(30)

式中：(ATA)-1是辅助因子。则目标位置估计为

(31)

这样可以求出两个估计量δx、δy。当A为方阵时，式(30)可以写成

(32)

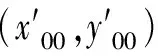
3 仿真实验结果

为了分析所提方法的可行性，对其进行了仿真验证。以图1为例设置室外城镇环境的大小为300 m×300 m，3个基站参与定位，各基站的位置分别设为(0,0)m、(0,300)m、(300,0)m。AOA、TOF的误差均服从均值为零、标准差为σAOA=4°和σTOF=30 m的高斯白噪声，散射模型圆半径设为50 m，散射体反射路径数量为10条。每个实验分别进行1 000次独立仿真以增加结果可信度。

3.1 模型之间参数比较

3.1.1 半径和散射路径数

为了分析在ROS、DOS模型中半径大小和散射路径数量对本文所提方法定位性能的影响，设置两种模型的半径变化范围为30～70 m，散射体路径数量变化范围为6～14条。ROS模型下和DOS模型下的仿真结果分别如图3(a)和(b)所示。

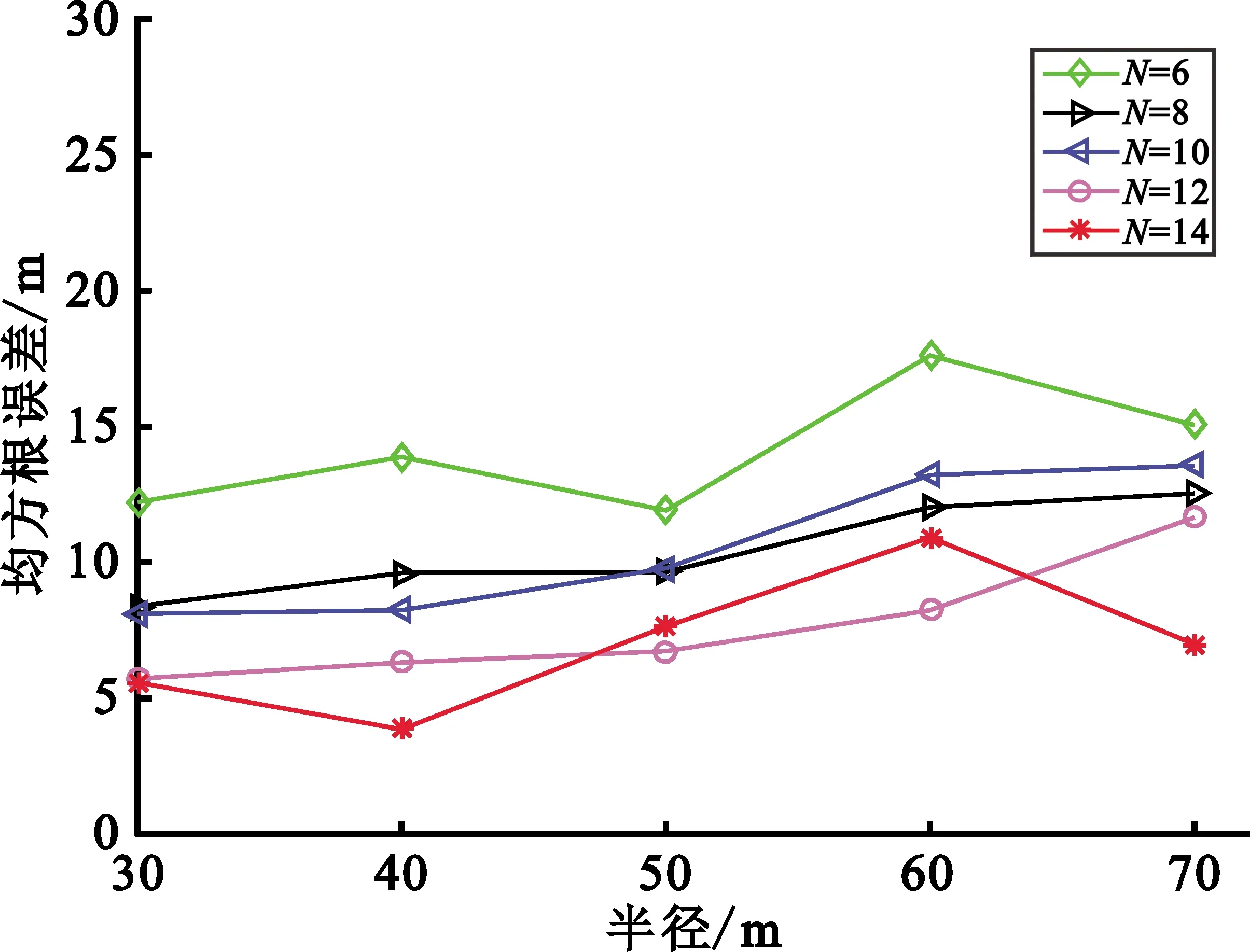
(a)ROS模型

从图3中可以看出，随着模型半径的增大，ROS模型中定位精度略微下降而DOS模型中定位精度较稳定；在半径和散射体数量相同的情况下，DOS模型的定位精度比ROS模型要高。由于约束区间是根据散射体AOA和路径长度设置的，DOS模型中散射体在圆盘区域均匀分布，散射体AOA较小，能使约束区间更小，且不受圆盘半径大小的影响，所以其定位结果较稳定精度也较高。而ROS模型中的散射体则分布在圆环上，因此半径增大时约束区间会相应增大，目标搜索区域会相应增大，导致LM算法解算时收敛效果有所下降，从而定位精度略微降低。同时，可以看出ROS和DOS模型中本文方法定位精度都随着散射体数目增加而提高。

3.1.2 AOA误差和TOF误差

图4(a)与(b)为ROS和DOS模型中没有根据散射体AOA和测得的路径长度添加约束区间的定位情况。模型半径为50 m，散射体数量n为10条，定位精度随AOA误差和TOF误差变化而变化的情况。从结果可以看出，AOA误差和TOF误差对定位精度影响较大，随着AOA误差和TOF误差增大，其定位误差精度也大幅度降低。而本文方法根据散射体AOA和测得的路径长度添加约束区间后的定位结果如图4(c)与(d)所示。

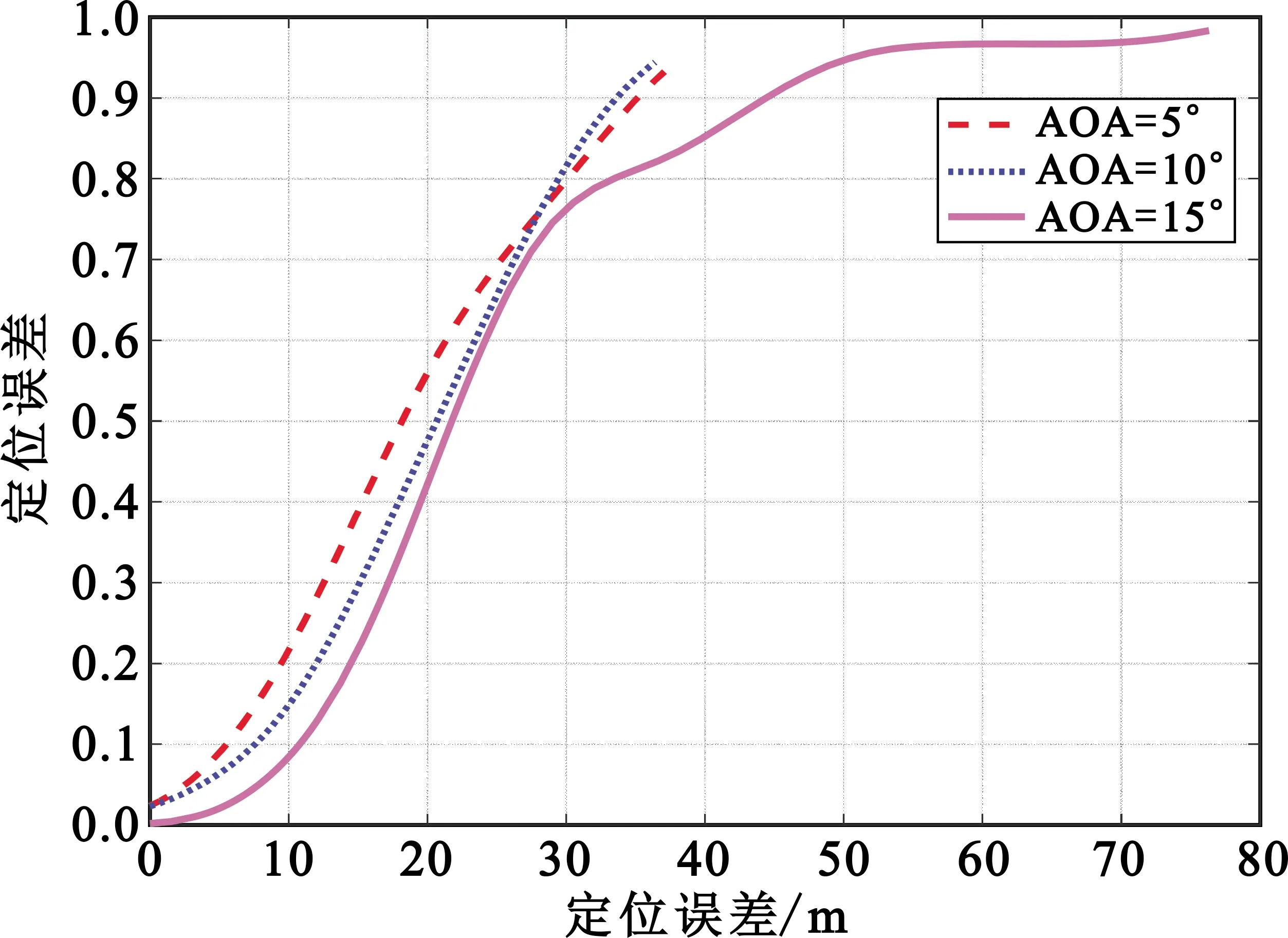
(a)AOA误差对定位性能的影响

由图4(c)～(d)可知，随着AOA误差和TOF误差增大，定位误差在很小的范围内波动，定位精度较稳定。这是因为添加约束区间后，会滤除掉误差较大的路径再寻找符合条件的观测值进行解算，这样会将精度控制在一定范围内；而误差较小时的路径在约束区间造成的定位误差小于约束区间内目标搜索模糊带来的误差，所以随着误差变化整个定位结果会在一定范围内波动。通过对比是否添加约束区间两种情况，本文提出的定位方法定位性能更加稳定可靠。

3.2 方法性能比较

图5为本文方法与传统AOA/TOA定位方法在ROS模型和DOS模型中得到的误差累计分布图。从图中可以看出，本文提出的定位方法能使定位误差迅速收敛，在ROS模型中有68%的概率使定位精度达到16 m，在DOS模型中有68%概率使定位精度达到8 m，而传统方法定位精度只能分别达到39 m和29 m，可见本文所提方法的解算结果非常接近最优解且能保证较高的定位精度。

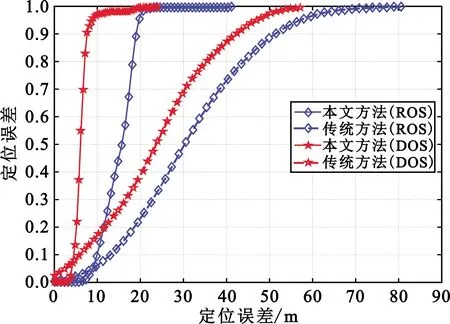
图5 本文方法与传统方法定位性能对比

图6为本文方法与传统方法在AOA误差和TOF误差变化时的定位误差变化情况。从图中可以看出，当AOA误差和TOF误差变化时，传统方法定位均方根误差都在22.76 m以上，而本文所提方法定位均方根误差都在15.12 m以内，而且本文均方根误差波动较传统方法要小。由于本文充分利用了散射体分布信息和基站、散射体、目标的几何位置关系，大幅度降低了信号NLOS传播误差对定位性能的影响，具有较高的定位精度和稳定性并且对NLOS误差敏感度较低。

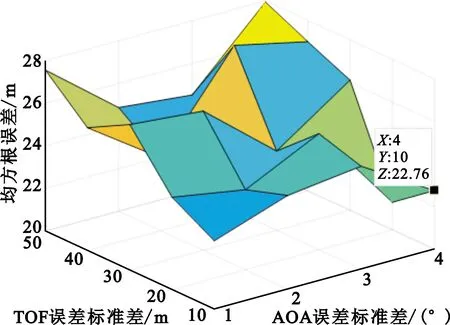
(a)传统方法

4 结束语

本文提出了一种基于角度重构和差分TOF的室外NLOS环境下多站定位方法，介绍了其基本原理并进行了仿真对比。区别于现有室外NLOS多站定位方法，本文利用差分TOF较大程度上解决了室外NLOS环境下定位信号收发不同步导致不易定位的问题，较好地利用了多径信息，避免使用复杂度较大的 NLOS 抑制算法进行定位，多基站联合定位也使定位精度大幅度提高。仿真结果表明，本文定位方法具有容错性好、稳定性强、收敛速度快等特点。

由于室外测试环境搭建困难，目前还未进行实际测试，所以下一步研究重点在于取得实测数据进行方案验证，并改进定位方案。