一种低轨双星窄带信号定位方法*

张宇阳，巢捷频

(中国西南电子技术研究所，成都 610036)

0 引 言

低轨双星系统由于构型稳定、系统代价小等优势，越来越受到无线电监测领域相关研究的关注[1-6]。系统最重要的一项功能是针对通信、雷达等辐射源信号，利用无源定位方法实现目标或干扰源位置的获取。当前低轨双星系统主要采用时差、频差联合定位体制，可实现多类型辐射源信号的快速高精度定位。

在轨道高度、星间距确定的条件下，时频差定位体制的精度主要受辐射源信号时差、频差测量精度影响。当前相关研究主要讨论信号带宽较宽的辐射源定位[5-8]，时差和频差测量精度都比较好，但缺少对窄带辐射源的定位讨论。在某些应用场景下，目标对象为低码速率通信信号、单音干扰等，这类信号可以获得很高的频差测量精度，但由于时差测量精度非常差，采用时频差定位体制难以获得高精度定位结果。本文针对该问题，提出一种基于多次频差观测量的高精度定位算法，实现低轨双星系统对窄带通信、单音干扰源等窄带信号的高精度定位。

1 定位原理

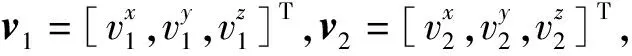
(1)

式中：c为光速。

一个频差方程可以表征地球球面上一条曲线描述的范围，即目标可能位置范围，理论上通过两组频差方程、两组曲线相交即可进行目标交点计算实现辐射源定位。两组曲线相交通常会有两个交点，一个为真实位置，一个为模糊点，实际应用中可通过左右比幅解模糊。图1表示了频差为-700 Hz和-1 200 Hz两条曲线相交的情况。

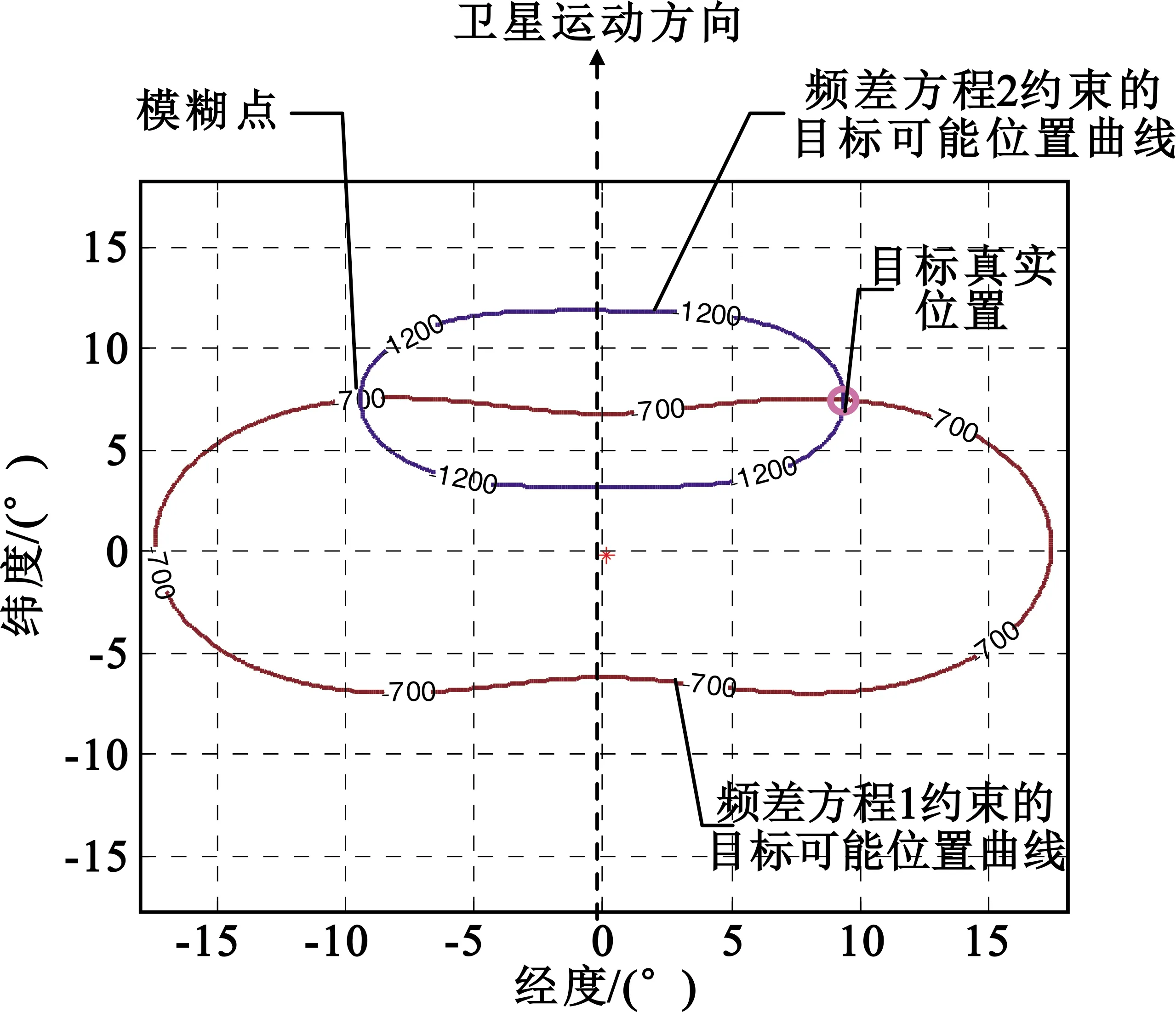
图1 双星频差定位原理

2 算法描述

基于双星频差定位原理，为了充分利用观测过程中获取到的辐射源频差信息，采用多次频差测量结果联合计算辐射源位置代价函数的方法进行定位，通过积累处理的方式提高定位精度。

设低轨双星系统在N个时刻对辐射源进行观测，且测量的频差可以表示为

(2)

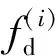
(3)

其中：

(4)

是位置为u的辐射源频差算子,c为光速。求解下式，即可获取目标位置：

(5)

通过上述分析，基于N次频差测量的辐射源定位处理步骤如下：

Step1 设定辐射源初始经纬度[α0,β0]，辐射源搜索范围γ。

Step2 以辐射源初始经纬度为中心，在搜索范围内，以分辨率λ，将搜索范围均匀划分成J×K二维网格，形成一系列的网格点e(0,0),e(0,1),…,e(0,J-1),e(1,0),…,e(J-1,K-1)。

Step3 对于每一个二维网格点e(j,k)，将地理坐标转换为地固坐标，表达为u(j,k)，其中j、k分别表示坐标序号。

Step4 计算N个时刻u(j,k)对应的频差值gi(u(j,k))，i=0,1,…，N-1。

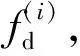
Step6 重复Step 3～5，直到所有J×K二维网格点完成计算，形成代价值集合P={p(j,k)}。

Step7 搜索P中最小值对应网格点，即为辐射源位置估计值。

辐射源位置估计精度与分辨率λ相关，而计算复杂度与搜索范围γ和分辨率λ相关，λ越小，计算复杂度越高。辐射源的搜索范围可由辐射源位置的粗测结果确定的可能区域范围或低轨双星系统的覆盖范围确定。为了平衡计算复杂度和精度，本文在搜索到最小位置对应的网格点后，采用插值的方法提高定位精度。

3 性能仿真

3.1 仿真分析参数

采用低轨圆轨道同轨双星系统为窄带信号定位性能分析场景，卫星初始时刻位置、速度参数如表1所示。

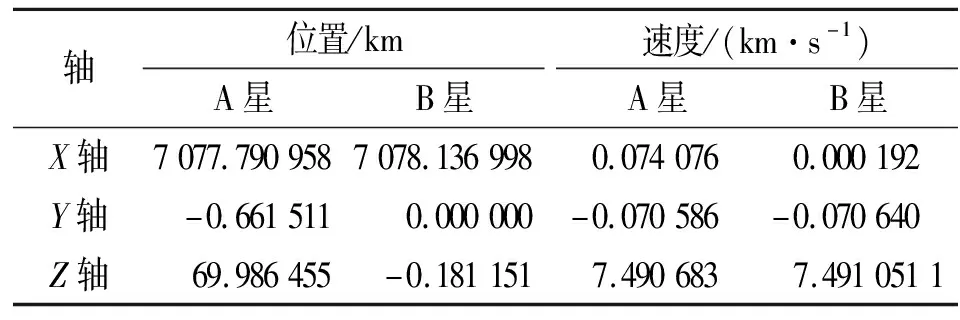
表1 仿真用的卫星初始时刻数据

仿真分析中，根据工程应用需求和可达到的能力，信号频率选择为200 MHz、1 GHz、2 GHz，频差测量精度设置0.1 Hz、0.2 Hz、0.5 Hz等。

3.2 与时频差定位方法对比分析

假设辐射源信号具备N次观测条件，采用时频差定位方法[7,10]可进行N次时频差测量，获得N个定位值，平均后输出1个值作为定位结果，即N次时频差测量结果累积获得1次定位结果。本算法基于N次频差测量值获得1个定位结果，观测条件完全一样。在信号频率1 GHz、信号带宽5 kHz时，距离卫星星下点1 000 km处目标，频差测量精度0.1 Hz，每秒观测1次，总共观测次数N=30，Monte-Carlo仿真1 000次时，时频差定位方法和本文算法的定位分布如图2所示，其中红点为目标真实位置，归一化到经纬度为(0°，0°)，可以发现本文算法优于传统算法。

(a)时频差定位算法

对不同带宽信号，时长相同，频差精度均取0.1 Hz，本文算法精度和时频差定位精度对比见表2。

表2 不同信号带宽定位精度对比

从仿真结果可以看出，对于相同时长但不同带宽信号，频差测量精度一样，但时差测量精度随带宽变小而降低；对于带宽大于25 kHz信号，采用时频差定位方法精度优于本文算法；对于带宽小于10 kHz及以下的窄带信号，由于时差测量精度逐步恶化，时频差定位结果变差；对于带宽1 kHz及以下信号，时频差定位方法基本不可用。本文算法由于频差精度随信号带宽不变，定位精度明显优于时频差定位方法，说明本文算法在针对带宽10 kHz以下信号时具有很强的实际应用价值。

3.3 算法性能分析

频差定位中，定位精度还与信号载频、频差测量精度、观测时长等因素相关。为了进一步评估算法适应能力，本文进行了不同条件下算法性能评估。

针对0.2 GHz、0.4 GHz、1 GHz、2 GHz等不同频点信号，累积观测时间20 s时，频差测量精度δfd为0.1～0.6 Hz条件下的CEP0.5定位性能如图3所示。

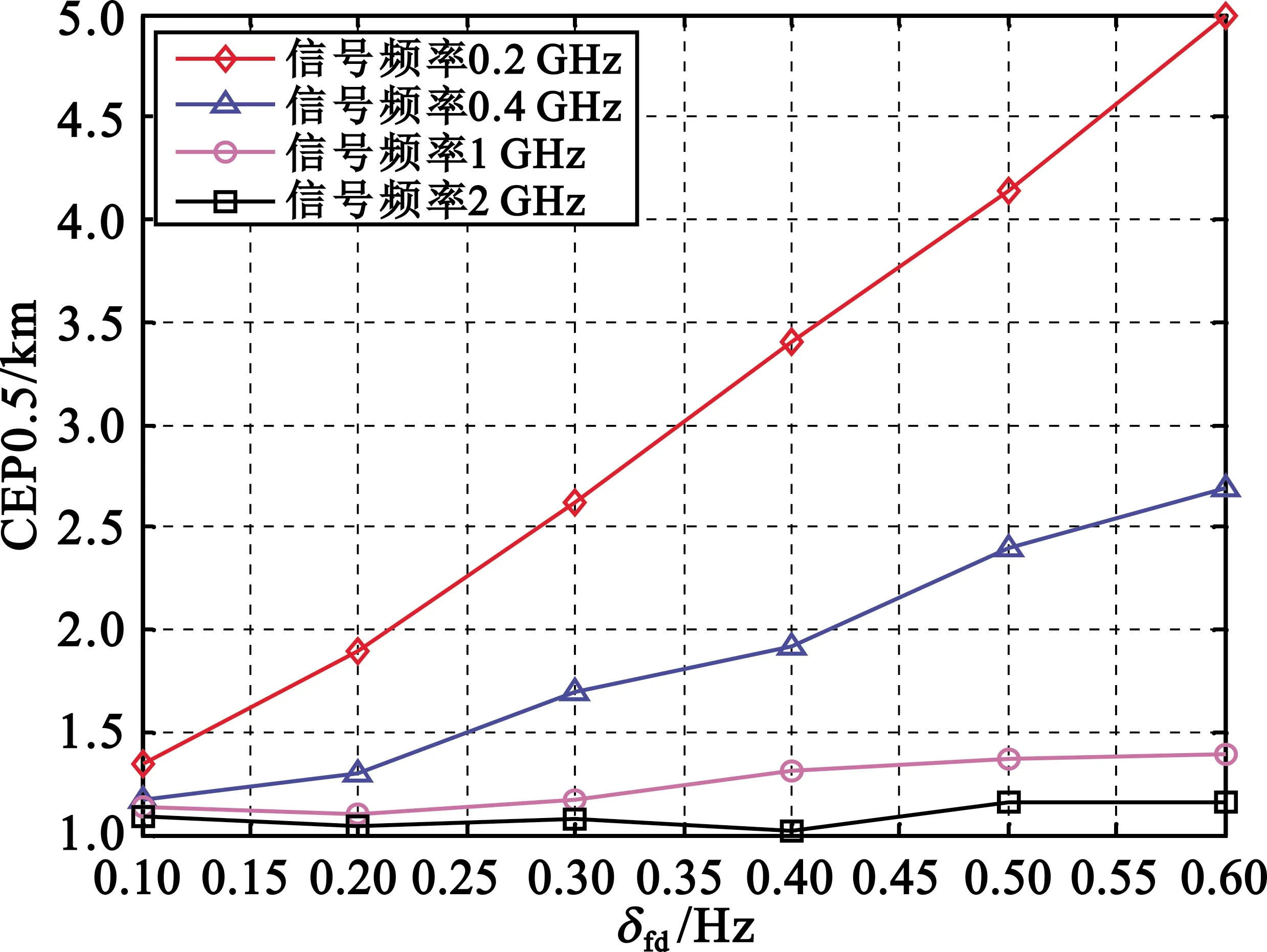
图3 频差测量误差对定位精度影响

从仿真结果可以看出，信号频差测量精度越高，定位精度越高；信号载频越小，频差测量误差对定位精度的影响越大。对于1 GHz以上信号，频差测量精度优于0.6 Hz，定位精度可达1.5 km；对于0.2 GHz以上信号，频差测量精度优于0.6 Hz，定位精度可达5 km。

另外一个影响定位精度的重要因素就是累积观测时间。针对0.2 GHz、0.4 GHz、1 GHz、2 GHz等不同频点信号，在频差测量精度0.1 Hz时，观测时间T为5～30 s条件下的CEP0.5定位性能如图4所示。

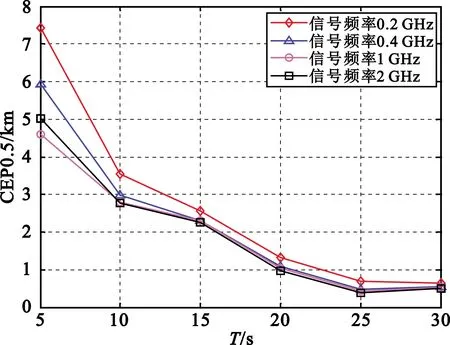
图4 观测时间对定位精度影响

从仿真结果可以看出，累积观测时间越长，定位精度越高，在信号累积时间小于15 s时，累积时间对不同频率信号定位精度影响较明显；累积观测时间优于20 s，对于0.2 GHz以上信号，定位精度可达1.5 km。算法仿真采用的条件与真实场景相同，仿真次数不影响该结论。

4 结束语

针对低轨双星系统对窄带辐射源的位置获取问题，本文利用多次频差测量联合处理实现对窄带辐射源信号的高精度定位，相比时频差定位平均的方法，定位精度更高，对窄带信号的适应能力更好，且能适应传统方法不能适应的单频信号，具有较强的工程应用价值。文中给出的仿真实例证明了该方法的有效性。后续将进一步研究计算量和精度之间的平衡关系，在保证精度的同时降低处理计算量。