激励力幅值对非线性能量阱系统全局分岔特性的影响研究
李 爽,楼京俊,柴 凯,刘树勇
(海军工程大学a.动力工程学院;b.舰船与海洋学院,武汉430033)
0 引 言
线性吸振器具有吸振频率固定且带宽极窄的特点,对于潜艇液压泵、辅冷泵这一类激励特性随直流幅压电机蓄电池电压变化的机械设备而言,线性吸振器吸振效果有所退化,往往达不到工程要求[1]。在线性吸振器中加入非线性因素理论上能够拓宽吸振频带[2],从而解决潜艇机械设备激励特性变化时的振动控制难题。非线性能量阱(Nonlinear Energy Sink,NES)正是一种引入本质非线性刚度的动力吸振装置[3],其能够通过共振俘获等非线性动力学行为在宽频范围内靶向吸收和耗散主结构的振动能量,从而达到抑制主结构瞬态或稳态振动的目的。正是由于这一特质,非线性能量阱技术近年来引起了国内外学者的广泛关注[4-8]。
最初,有关NES的研究工作主要集中于对瞬态振动的抑制,在此类系统中,关于靶能量传递、瞬态共振俘获等原理研究已经比较透彻。直至Starosvetsky、Gendelman 等[9-10]发现在耦合NES 子系统的稳态振动系统中,同样存在一种类似于靶能量传递的响应形式,并将其称为强调制响应(strongly modu⁃lated response,SMR),国外学者Gourc[11]、Kerschen 等[12],以及国内学者孔宪仁等[13]、Zhang 等[14]也相继开展了该领域的研究工作。强调制响应本质上属于非线性松弛振荡运动[15-17](relaxation-type motion),系统响应存在快慢变化过程,同时与系统初始能量存在密切的关系。研究该响应需要首先研究清楚系统平衡点类型,而折奇点这一类型平衡点通过局部分岔分析是观察不到的[18]。这对研究NES 这一类高维非线性系统造成了很大的难度。
国内刘良坤等[19]开展了NES 吸振系统受基底简谐激励时产生SMR 的充要条件研究,本文在此基础上着重分析主系统受简谐激励力作用时,激励力幅值对NES吸振系统全局分岔特性的影响,并用相轨迹法验证了周期吸引子与折奇点随激励力幅值的演变过程,不仅是对文献[19]的拓展与创新,更是对后续研究NES吸振系统的全局性态奠定了一定的理论基础。
1 系统模型
本文所研究系统模型如图1 所示。其中单自由度线性主系统受外界简谐激励作用,下端安装在刚性基座上,上端与单自由度非线性能量阱耦合相连,且非线性能量阱满足本质非线性刚度特性。
根据牛顿第二定律,系统运动学方程为

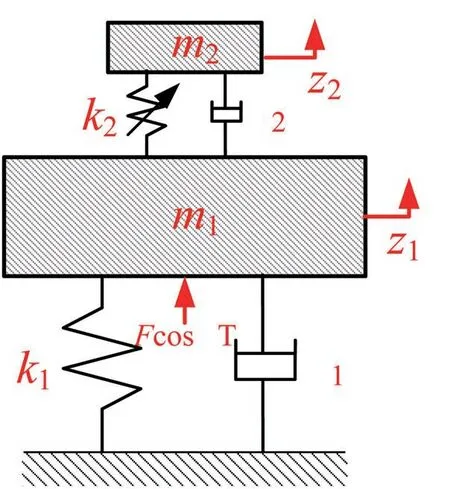
图1 非线性能量阱吸振系统动力学模型Fig.1 Dynamic model of the coupled NES absorption system
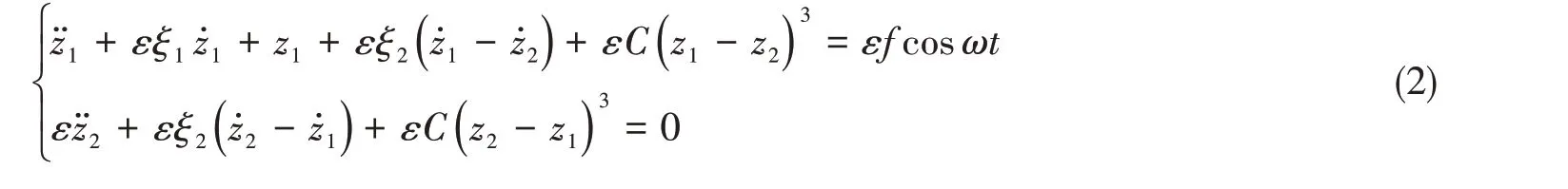
主要考虑激励频率接近主系统固有频率时的1:1:1主共振情形,令ω = 1 + εσ,这里σ为激励频率失调参数。作坐标变换u = z1+ εz2、v= z1- z2,并对系统进行降维,引入复变量参数

式中j 为虚数单位,ψi是关于变量u、v 的慢变调制幅值,i=1,2。在不考虑主系统阻尼情况下,将式(3)代入式(2)中,通过平均化过程消除快变响应部分,可得方程

2 系统全局分岔特性分析
引入新的时间尺度τk= εkt,k = 0,1,…,并令φ2= φ2( τ0,τ0,…),采用多尺度法展开
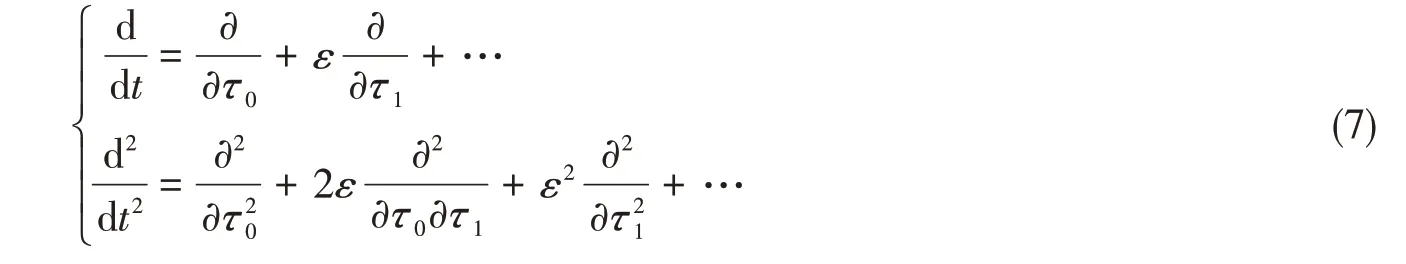
将式(7)代入到式(6)中,忽略高阶项,可得到关于ε的不同阶次方程
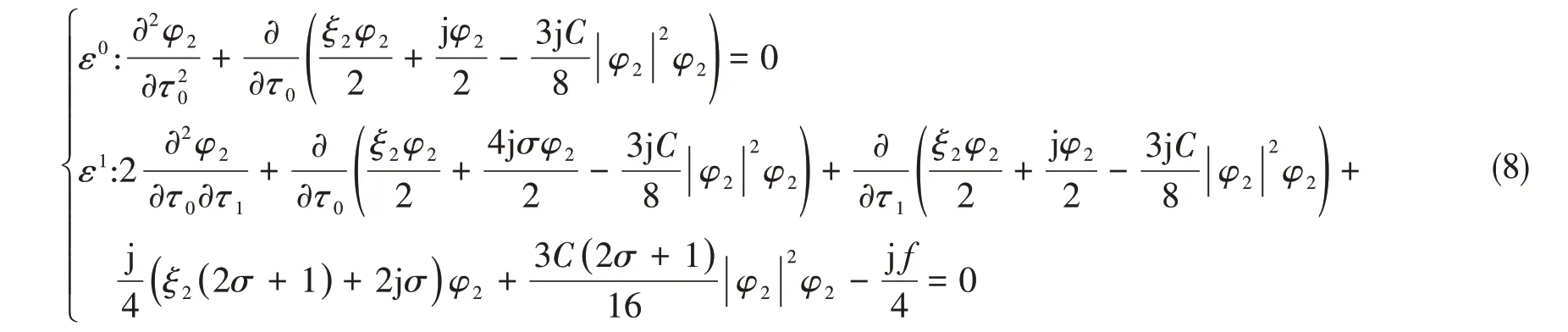
首先考虑φ2在慢变时间τ1上的近似解,φ2关于快变时间τ0积分可得第一个积分方程
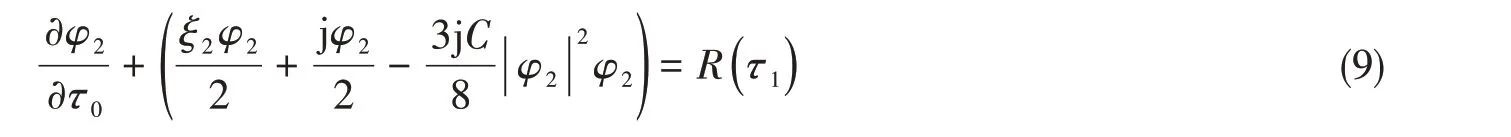
式中,R 是关于τ1的任意函数。令∂φ2/∂τ0= 0,由式(9)可知,系统平衡点Φ( τ1)只与慢变时间τ1有关,满足方程

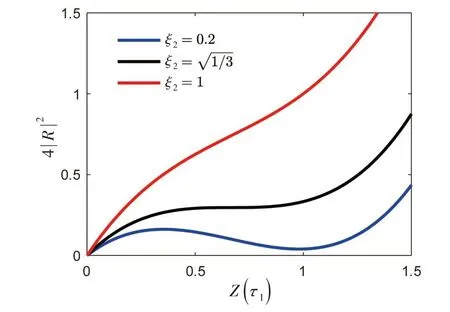
图2 不同阻尼系数下f ( Z )曲线Fig.2 Curves of f ( Z )under different damping ratios

图3 系统慢不变流形Fig.3 Slow invariant manifold of the system

将式(16)写成函数形式

由数学知识易知,式(17)具有两类平衡点,第一类是普通吸引子,对应系统周期解;第二类是折奇点。其中普通吸引子满足条件

而折奇点满足条件
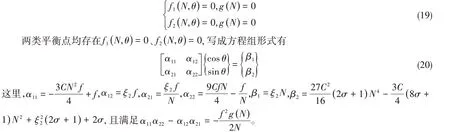
对于第一类平衡点,由于g( N )≠0,可得α11α22- α12α21≠0,系数矩阵为满秩矩阵,因此式(20)具有唯一解,且满足如下表达式

由于N1≤N2,可得f1c≤f2c。由上述分析可知,当激励力幅值f ≤f1c,无折奇点出现;当f1c≤f ≤f2c,仅有下折奇点出现;当f ≥f2c上下奇点才能同时出现。
3 激励力幅值对全局分岔特性的影响
参考文献[19],选取系统参数C = 4/3,ξ2= 0.2,σ = 0,系统周期吸引子分岔情况如图4所示。从图中可知,激励力幅值增加时,系统只存在一个周期解,其中黑色实线为稳定周期解,黑色虚线为不稳定周期解,不稳定解区域位于折叠线N1、N2之间。另外,通过式(21)可求得折叠线N1、N2对应的分岔点激励力大小分别为fb1= 0.241 9,fb2= 0.989 2。
三维平面( N,θ,f )以及二维平面( N,θ )内系统全局分岔图如图5 所示。图中‘rp’代表周期吸引子,‘fs1’、‘fs2’分别代表上、下折奇点,‘bp1’、‘bp2’为周期吸引子分岔点,此外,通过式(23)可求得折奇点对应的分岔点为fc1= 0.176 0、fc2= 0.984 4,因此有fc1<fb1<fc2<fb2。从图中可知,当激励幅值f <fc1时,系统只存在一个稳定的周期吸引子;当f = fc1,系统平衡点出现亚临界分岔,在折叠线N1处产生一对不稳定的下折奇点,在fc1<f <fb1范围内,系统存在一对不稳定的下折奇点以及一个稳定的周期吸引子;进一步增大f,当f = fb1时,周期吸引子由稳定解退化为不稳定解,同时下折奇点由不稳定解变为稳定解,在fb1<f <fc2范围内,此时系统存在一对稳定的下折奇点和一个不稳定的周期吸引子;当f = fc2时,系统平衡点再次出现亚临界分岔,此时系统演变出一对稳定的上折奇点,在fc2<f <fb2范围内,此时系统存在一对稳定的下折奇点、一对稳定的上折奇点以及一个不稳定的周期吸引子;当f = fb2时,上折奇点由稳定解退化为不稳定解,同时周期吸引子再次发生Hopf分岔,由不稳定解变为稳定解,在f >fb2范围内,此时系统存在一对稳定的下折奇点,一个稳定的周期吸引子以及一对不稳定的上折奇点。
从上述分析可知,激励力幅值对所述系统平衡点个数以及吸引子类型影响都比较显著,随着激励幅值的变化,在fc1、fb1、fc2、fb2等分岔点处,系统平衡点会出现亚临界分岔、Hopf分岔等复杂的非线性动力学现象。需要说明的是,文中有关平衡点稳定性判断可参考文献[20],这里不再赘述。

图4 周期吸引子分岔情况Fig.4 Bifurcation diagram of the system periodic attractor
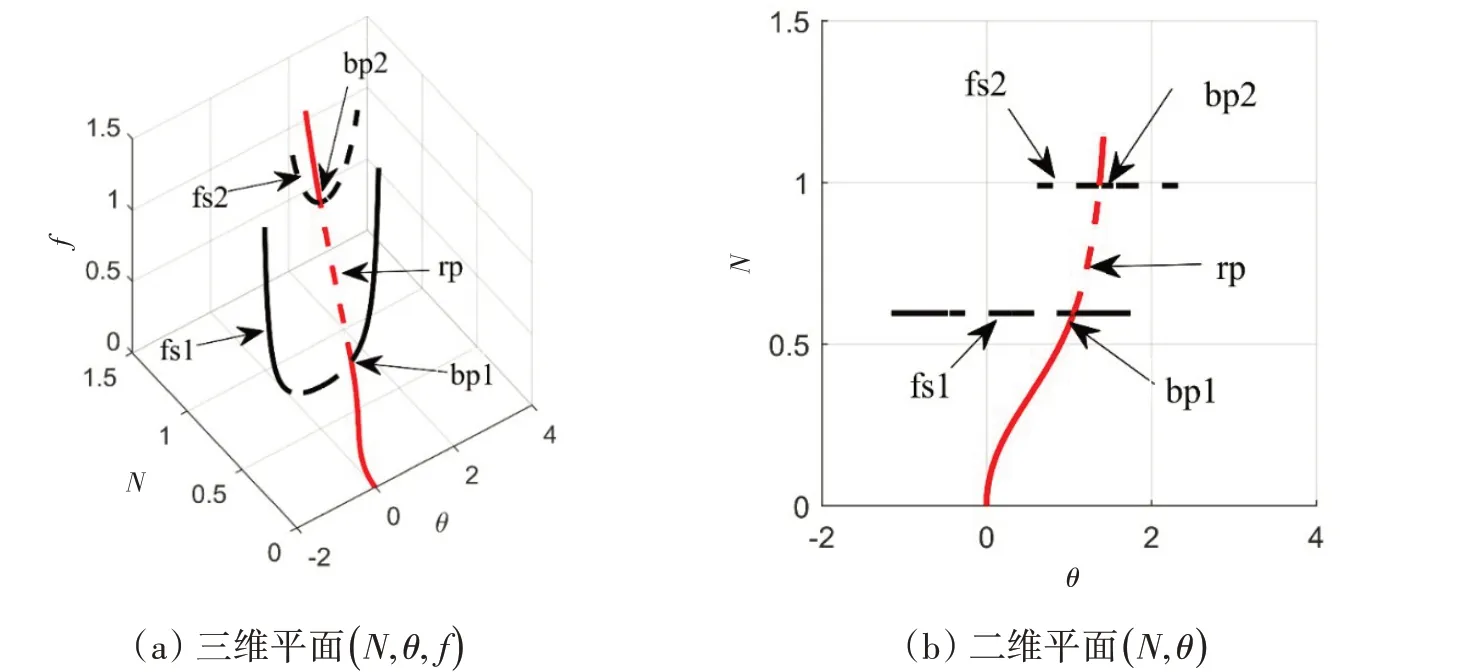
图5 系统全局分岔图Fig.5 The global bifurcation diagram of the system
4 相轨迹分析
保持参数C=4/3,ξ2= 0.2,σ = 0 不变,结合ode45 数值法与Matlab streamline 流形函数绘制不同激励力幅值下系统响应的相轨迹,如图6 所示。图中纵坐标为响应幅值N,横坐标为相位θ,θ ⊂( 0,2π ),蓝色曲线为慢不变流形相轨迹,红色曲线对应折叠线N1和N2,N1~N2之间为系统响应的不稳定区域,另外系统普通吸引子在图中用红色“□”标注,折奇点用红色“·”标注。
从图6(a)中可知,当f=0 时,从折叠线N2上方出发的相轨迹都可以回到N2,然而从N1出发的相轨迹不能返回至N1。这意味着相轨迹从上稳定分支出发时能跳跃至下稳定分支,而从下稳定分支出发的相轨迹不能跳跃至上稳定分支。这与实际系统也是相符合的,因为不存在外界激励时,由于阻尼的存在,系统能量会逐渐被耗散,直至趋于稳定。
从图6(b)中可知,当f=0.1 时,对应f <fc1,此时系统只存在一个稳定的周期吸引点,不存在折奇点,所有的相轨迹最终都流入至该吸引子。
从图6(c)中可知,当f=0.18时,对应f略大于fc1,此时存在一个周期吸引子与一对下折奇点。另外通过相轨迹特性可知,左侧下折奇点为结点,右侧下折奇点为鞍点,从鞍点右边出发的相轨迹都被吸引至周期吸引子,结点左边以及折叠线N1右边部分相轨迹吸引至结点,而结点与鞍点之间的相轨迹则有可能返回至折叠线N1。
从图6(d)中可知,当f=0.5 时,对应fb1<f <fc2,系统性态发生了非常显著的变化。首先,和f=0.18相比,周期吸引子消失,同时鞍点与结点沿着下折叠线往两侧移动,其中结点往左移动,而鞍点往右侧移动,导致两者之间距离扩大,最终能够回到N1的相轨迹区域也在增大。值得注意的是,在绘制相轨迹过程中,只取了一个周期(0,2π),当结点运动超过最左侧时,又重新在右端出现。另外,从相轨迹特征可知,折奇点性质已经由鞍结点通过碰撞演化成了稳定的焦点。
从图6(e)中可知,当f=0.987 时,对应fc2<f <fb2,此时在上折叠线N2上出现一对鞍结点,而下折叠线N1上的一对稳定焦点依然存在。进一步增大激励幅值,当f=1时,对应f >fb2,如图6(f)所示,折叠线N2上鞍结点演化成了一对不稳定的鞍点,同时在折叠线N2上部分出现了稳定的周期吸引子。
总结可得,激励力幅值对系统全局分岔特性的影响规律如表1所示。

图6 不同激励力幅值下系统响应相轨迹Fig.6 Phase trajectory of the system response under different excitation force amplitudes

表1 系统分岔点及分岔现象Tab.1 Bifurcation points and phenomenon of the system
5 结 语
在质量比ε为小参数条件下,本文结合复变量平均法、多尺度法以及相轨迹法研究了激励力幅值对单自由度非线性能量阱吸振系统的全局分岔特性的影响。由分析结果可知:激励力幅值对所研究系统平衡点个数以及吸引子类型影响都比较显著,除周期吸引子外,系统还可能存在折奇点这一类通过局部分岔观察不到的平衡点类型;另外,随着激励力幅值的增加,系统将呈现亚临界分岔、Hopf分岔等非常复杂的演变行为,系统相轨迹也会发生明显的改变。这为后续全面研究非线性能量阱吸振系统的全局性态打下了理论基础。

