深吃水半潜生产平台涡激运动特性研究及其参数化分析
胡晓峰,张新曙,李聪洲,尤云祥
(上海交通大学海洋工程国家重点实验室高新船舶与深海开发装备协同创新中心,上海200240)
0 引 言
近年来,国际海洋油气的勘探开发不断由浅海转向深海,因此深吃水半潜平台得以迅速发展。传统半潜平台在波浪中的垂向运动响应较大,而深吃水半潜平台在波浪中的垂向运动性能则有了明显提高。但是,由于平台吃水的增加,也大幅提升了平台所受的流向阻力和横向升力。较大的横向升力导致平台产生显著的涡激运动(Vortex Induced Motions,VIM),深吃水半潜平台的涡激运动会严重影响平台立管系统和系泊系统的疲劳寿命[1-2]。
与单柱式平台不同,深吃水半潜平台由于多柱之间流场的相互干扰,其涡激运动的特性更加复杂。目前研究涡激运动的方法主要有:模型实验、计算流体力学(Computational Fluid Dynamics,CFD)数值模拟和实地监测。已有许多学者针对深吃水半潜平台涡激运动特性进行了相关模型实验研究以及CFD 数值模拟研究。Waals 等[3]通过模型实验对比分析了双浮箱与四浮箱深吃水半潜平台和传统半潜平台的涡激运动。Hong 等[4]进行了深吃水半潜平台的耐波性实验,发现半潜平台涡激运动的运动幅值不仅与流速有关,还与波浪有关。Gonçalves 等[5]通过模型实验研究了入射角及附体对深吃水半潜平台涡激运动的影响。谷家扬等[6]通过模型实验和数值模拟方法研究了不同流向角下深吃水张力腿平台的涡激特性和水动力性能。Lee等[7]对深吃水半潜平台涡激运动进行了实尺度及模型尺度数值模拟研究。
分离涡(Detached-Eddy Simulation,DES)[8]方法(也称为DES97 方法)是一种结合了雷诺平均方法(Reynolds-Averaged Navier-Stokes,RANS)与大涡模拟(Large Eddy Simulation,LES)方法的混合方法,已被证实是一种有效的数值方法。DES方法在近壁面使用RANS方法进行模拟,而在远离壁面的分离区使用LES方法模拟来捕捉大尺度分离流动。
本文采用改进的延迟分离涡方法(Improved Delayed Detached-Eddy Simulation,IDDES)[9]对一深吃水半潜平台的涡激运动进行数值模拟研究,对比分析不同流向角及约化速度下平台的涡激运动响应,并探讨立柱倒角以及吃水对半潜平台涡激运动的影响。
1 数值方法
1.1 改进的延迟分离涡方法(IDDES)
IDDES是在DES基础上提出的一种改进方法。它结合了两类RANS/LES方法,一类是延迟的脱体涡方法(DDES),另一类为使用壁面模型的大涡模拟(WMLES),其目的是消除早期DES 方法中对网格划分的依赖性,同时进一步提高近壁面附近流场的求解精度。

式中,d为离壁面的最短距离,Δ = max( )Δx,Δy,Δz 是三个方向上局部网格尺寸的最大值,Cdes为0.65。
从式(1)可以看出DES97 方法中,RANS 到LES 的转换完全取决于网格尺度大小。在某些情况下会导致RANS提前转换到LES,出现模型应力耗散(Modeled Stress Depletion,MSD)现象,从而导致网格诱导分离(Grid-Induced Separation, GID)。同时,DES97 方法还存在对数层不匹配(Log-Layer Mis⁃match, LLM)的问题[9]。在此基础上,Spalart 等[10]提出延迟分离涡(Delayed Detached-Eddy Simulation,DDES)方法来解决GID问题。DDES方法对长度尺度的定义做了修改,具体如下:

式中,fd为延迟过渡函数,fd能避免LES在边界层内进行求解,从而解决了GID问题。而DDES依然无法解决在边界层内部的对数层不匹配的问题,因此进一步发展了IDEES 方法,其将DDES 方法与WM⁃LES(Wall-Modelling LES)方法相结合。同时,lDDES中亚格子尺度Δ 的定义对有界流中不同的流动区域,无法给出一个普适的亚格子模型常数,从而导致不准确的流场求解。因此,IDDES 重新定义了长度尺度lIDDES,其表达式如下:

式中,下标d和e分别为与延迟函数和上升函数相关的符号[9],
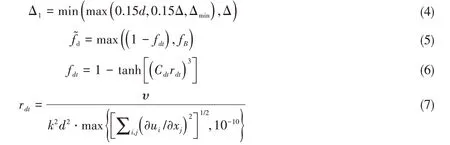
其中,Δmin为网格中心到相邻网格的最小距离,ψ 为低雷诺数修正函数,υ为运动粘性系数,∂ui/∂xj为速度梯度,fB为混合函数,Cdt为模型常量,Cdes取0.65,fe为转换函数,具体的参数定义参见文献[9]。
IDDES 方法通过入流条件中湍流信息的判定,即当rdt≪1 时,fdt≈1,͂退化为WMLES 的长度形式:
右胸前导联R波增高,R/S>1除了有侧壁心肌梗死的原因,还有其他多种原因,应注意鉴别,① 右室肥厚:有右室高压伴电轴右偏,肺型P波,T波通常低平或倒置,V7~V9导联无梗死图形。② 右束支阻滞:可出现高而宽的R波,可有钝挫,并继以ST段下移和T波倒置,SV5~V6变钝。③ A型预激综合征:各导联均有预激波,PR间期<0.12 s。④ 右位心:V1~V6导联R波进行性降低,QRS电轴出现特征性右偏,后背导联无梗死图形,肢体导联心电图也出现相应的变化。少数人为正常变异,可由逆钟向转位所致,但ST-T段正常。

否则,fe=͂退化为DDES的长度形式:

IDDES有效解决了DES类方法在处理大分离流动中所产生的模型应力耗散和对数层不匹配的问题,从而提高了高雷诺数下大分离流动的数值求解精度。
1.2 数值模型
本文以水池模型实验[11]的半潜平台作为计算模型,忽略了附体等因素的影响,其主要尺度参数如图1和表1所示,采用的缩尺比为1:100。

表1 平台的主尺度参数Tab.1 The main dimensions of the prototype
由于深吃水半潜平台的涡激运动主要发生在纵向、横向以及艏摇三个水平方向上,因此采用4根水平线性弹簧来等效系泊系统,从而模拟实际平台的水平运动的刚度,弹簧布置方式及流向角的定义如图2所示。其中xoy坐标系为大地坐标系,x'oy'坐标系为随体坐标系,θ为流向角。本文计算的流向角θ包括0°、22.5°和45°。

图1 平台的主尺度定义Fig.1 Main dimensions of the semi-submersible platform

图2 流向角定义与弹簧布置方式Fig.2 Definitions of current incidence angles and spring system
1.3 计算域与网格划分
计算域及边界条件的选取如图3 所示,入口边界距离平台中心为20D,两侧边界距离平台中心均为15D,计算域高度为6D。其中,入口边界条件设为速度入口,出口边界条件设为压力出口,计算域两侧边界均设为速度入口,平台表面和计算域底部设为无滑移壁面。由于计算工况中,傅汝德数Fr均很小,自由面的兴波成分较少,因此在研究涡激运动时暂不考虑自由液面对涡激运动的影响,将计算域上边界设为对称面边界条件。

图3 计算域和边界条件Fig.3 Computational domain and boundary conditions
在进行网格划分时,将计算域划分为三个区域,分别为近壁面区、尾流区以及远场区。网格划分的示意图如图4 所示。对不同区域的网格尺寸进行单独加密,近壁面区、尾流区以及远场区的网格尺寸大小分别为0.035D,0.07D 和0.28D。边界层网格数量为20层,y+值取小于1,边界层网格的增长率为1.2。为了减小网格差异导致的数值耗散,各区域之间的网格进行平滑过渡。

图4 网格划分示意图Fig.4 Grid distribution
2 数值结果
本文计算了半潜平台纵向、横向以及艏摇方向上的涡激运动响应,并采用Hilbert-Huang 变换(HHT)对计算结果进行处理,取HHT 处理后得到的运动幅值的前10%最大幅值的平均值来定义三个方向上的特征响应幅值[11],分别用Ax/D、Ay/D 和Ayaw表示纵向、横向以及艏摇方向上涡激运动响应的特征幅值。
约化速度Vr是与平台涡激运动特性相关的重要参数,其定义如下:

式中,T0为静水中横向运动的固有周期,U为来流速度,Dc为立柱的特征长度,其定义为

2.1 网格收敛性分析
本文选取三套不同网格尺度的网格进行收敛分析,具体网格尺寸如表2所示,其中D为立柱宽度。对流向角为45°、约化速度Vr= 6.76的工况进行计算,横向运动响应的计算结果如图5所示,其中无量纲时间步长t = ΔtU/D,Δt为时间步长。

表2 网格收敛性分析Tab.2 Sensitivity of the results to different grids

图5 流向角为45°,约化速度Vr = 6.76时的网格收敛性分析计算结果Fig.5 Sensitivity of computational charac⁃teristic amplitudes for transverse motions to different grids and time step sizes for 45°current incidence at Vr = 6.76
对比三套网格的计算结果可知:标准网格(G2)与精细网格(G3)的计算结果比较接近,而粗糙网格(G1)的计算结果则比其他两套网格的计算结果要小;无量纲时间步长t=0.02 时计算结果与t=0.01 的计算结果差别不大,而t=0.04 时计算结果则与前两者差距较大。综合计算成本和效率,本文选取G2 这套网格以及t=0.02来进行数值模拟。
2.2 自由衰减实验
为了校核数值计算中线性弹簧系统的刚度,首先对0°和45°流向角进行了自由衰减实验,并将平台运动的固有周期与模型实验结果进行比较。对于横向运动的衰减实验,给定初始位移为y/D=0.5;对于艏摇衰减实验,给定的初始转角为1°。

图6 0°和45°流向角下的横向衰减曲线Fig.6 Free decay tests of transverse motions for 0°and 45°current incidences
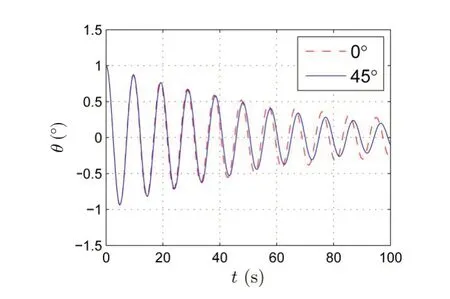
图7 0°和45°流向角下的艏摇衰减曲线Fig.7 Free decay tests of yaw motions for 0°and 45°current incidences
图6和图7分别给出了0°和45°流向角下横向及艏摇方向自由衰减运动的时间历程曲线。将衰减曲线进行快速傅里叶分析,从而得到平台的运动固有周期。表3 为计算所得固有周期与模型实验所得固有周期的比较结果,从表中可以看出,数值模拟的固有周期与模型实验结果吻合较好,最大的误差在2.7%左右,证明了数值计算中等效系泊系统的有效性。

表3 运动固有周期的比较Tab.3 Comparison of natural periods
2.3 涡激运动响应
图8 为0°、22.5°和45°流向角下纵向涡激运动响应的计算结果,其中模型实验结果参见文献[3]。从图中可以看出,数值模拟结果与模型实验结果吻合良好。不同流向角下纵向运动响应随约化速度的变化规律不同。当约化速度在7.0 附近时,22.5°流向角下的纵向运动存在最大峰值点,其运动响应幅值明显大于0°和45°流向角下的运动响应幅值。当3.0<Vr<13.0 时,45°流向角下的纵向运动响应随约化速度呈线性增加,未出现最大峰值点;而0°流向角下的纵向运动响应幅值则是先增大后减小,之后稳定在0.06附近。不同流向角下纵向运动特性的差异可能归结于不同流向角下的流向阻力差异。

图8 纵向运动响应幅值Fig.8 Characteristic amplitudes of in-line motions

图9 横向运动响应幅值Fig.9 Characteristic amplitudes of transverse motions
横向涡激运动响应的计算结果如图9所示,可以看出横向运动响应幅值明显大于纵向运动响应幅值。由图可知,0°和45°流向角下的计算结果随约化速度的变化趋势与模型实验结果基本一致,45°流向角峰值点处的计算结果略小于实验值。22.5°和45°流向角下,横向涡激运动响应存在显著的共振区,发生频率锁定现象,使得横向运动的运动幅值大幅增加,锁定区域为6.0<Vr<8.0。对于0°流向角,锁定区域相对滞后,发生在9.0<Vr<11.0,这可能是由于不同流向角下各立柱间流场的干扰特性不同所致。此外,22.5°流向角下的最大横向运动响应幅值明显大于0°和45°流向角下的最大横向运动响应幅值。
图10 给出了不同约化速度下平台的艏摇运动响应。从图中可知,计算结果与实验值基本吻合。对比于纵向和横向涡激运动,艏摇涡激运动响应在0°、22.5°和45°三种流向角下均未出现明显的共振区和最大峰值点。艏摇运动响应随约化速度Vr的增加而不断增大,未出现自制现象,因而推测艏摇涡激运动更可能与驰振相关。

图10 艏摇运动响应幅值Fig.10 Characteristic amplitudes of yaw motions
2.4 平台立柱倒角对涡激运动的影响
由于平台涡激运动的起因是立柱尾部的周期性漩涡脱落,因而其立柱尾部的流动分离形式会对涡激运动产生重要的影响。方柱的分离点通常发生在柱体倒角边缘处,因而不同大小的倒角可能影响到其流动分离的形式。本文研究了不同立柱倒角对深吃水半潜平台涡激运动的影响,同时选择了两种不同的倒角方式,如图11所示。其中,方法A 只改变立柱的某一边的倒角,方法B为立柱四个边的倒角均发生改变。选取45°流向角下,Vr=6.76的工况进行数值模拟计算,计算的倒角半径R 包括0.09D、0.21D 和0.33D三种。
图12 和图13 分别为45°流向角,Vr=6.76 时,不同倒角下的横向运动响应和艏摇运动响应。由图12和图13可知,对于A类型倒角,倒角半径尺寸对横向运动响应和艏摇运动响应的影响很小,而对于B类型倒角,横向运动响应和艏摇运动响应均随倒角半径增加而变大。

图11 立柱横剖面上的倒角示意图Fig.11 Details of the corner geometries for the cross section

图12 不同倒角半径下的横向运动响应Fig.12 Characteristic amplitudes of transverse motions with different column corner radii

图13 不同倒角半径下的艏摇运动响应Fig.13 Yaw characteristic amplitudes with different column corner radii
2.5 半潜平台吃水对涡激运动的影响
在前文基础上,本节进一步研究了五种不同吃水(H/D=0.23、H/D=0.7、H/D=0.9、H/D=1.14 和H/D=1.5)状态下半潜平台的涡激运动,图14和图15分别为45°流向角时,不同吃水状态下半潜平台的横向运动响应和艏摇运动响应。由图14和图15可知,随着吃水的增加,半潜平台的横向运动响应和艏摇运动响应均相应增大。当H/D=1.14和H/D=1.5时,横向运动有明显的频率锁定现象,而吃水较小(H/D≤0.9)时,半潜平台的横向运动则无明显频率锁定现象。

图14 45°流向角下不同吃水时的横向运动响应Fig.14 Characteristic amplitudes of transverse motions for 45°incidence with different draft conditions

图15 45°流向角下不同吃水时的艏摇运动响应Fig.15 Yaw characteristic amplitudes for 45°incidence with different draft conditions
3 结 论
本文基于改进的延迟分离涡方法(IDDES)实现了深吃水半潜平台涡激运动的三维数值模拟,对不同流向角下的涡激运动特性进行了研究,并探讨了立柱倒角半径以及立柱吃水对半潜平台涡激运动特性的影响规律,主要结论如下:
(1)通过对比实验结果发现,数值模拟的纵向运动、横向运动及艏摇运动幅值与实验值吻合良好,有效验证了本文所采用数值方法的合理性。
(2)半潜平台横向运动幅值明显大于纵向运动幅值,且横向运动出现明显的频率锁定现象,22.5°和45°流向角下横向运动的锁定区域为6.0<Vr<8.0,而0°流向角下横向运动的锁定区域则滞后于22.5°和45°流向角,这可能是因为不同流向角下各立柱间流场的干扰特性不同。此外,在3.0<Vr<13.0 区间内,半潜平台各流向角的艏摇运动响应随Vr增加均呈线性递增的变化趋势。
(3)当只改变平台立柱单边的倒角半径时,倒角半径尺寸对半潜平台横向运动响应和艏摇运动响应的影响很小,而同时改变立柱四边倒角时,随着立柱倒角半径的增加,半潜平台的涡激运动幅值更加显著。
(4)半潜平台的横向运动响应和艏摇运动幅值随平台的吃水增加而增大,而当吃水H/D≤0.9 时,半潜平台在不同约化速度下的横向运动幅值均很小,且无明显的频率锁定现象。

