基于严格等式约束的推力分配算法研究

赵 伟，刘焕卫

（烟台大学海洋学院，山东烟台264005）

0 引 言

为了满足作业要求，半潜式海洋平台需要装备能够控制其位置或航行轨迹的定位装置，常见的有锚泊定位、动力定位以及锚泊辅助动力定位。随着海洋石油开采不断朝着深水领域发展，锚泊定位因为自重过大等原因不再适用，而动力定位系统具有定位精度高、操作性灵活和不受水深限制等优点使其具有广泛的应用前景。动力定位系统能够抵抗外部环境的干扰，控制平台在横荡、纵荡以及艏摇三个自由度的慢漂移运动，使其在一定的范围内正常作业。作为动力定位系统的执行装置，推进器良好的推力分配结果不仅关系到平台的定位能力，而且对节约成本特别是燃油消耗具有很重要的意义。为了满足海洋钻井平台作业时的定位精度及可靠性，一般装备有动力定位的船舶配有比常规船舶更多种类和数量的推进器，从而在硬件冗余上提高系统的可靠性，但这也给推力分配的优化带来了新的课题。

动力定位系统主要控制海洋钻井平台在3 个自由度上的运动，而推进器种类和数量的增多使得输入的维度要多于所需控制的自由度，这属于过驱动问题。针对实时控制系统，过驱动推力分配要在采样间隔内迅速寻找一个最优推力角和推力的组合来满足控制器输出的需求控制力和力矩，因此可以用最优化的方法解决过驱动系统的推力分配问题[1]。目前针对推力优化问题的解决主要分为线性二次无约束分配、线性二次约束分配以及非线性约束分配三类。序列二次规划法是最常用的优化方法，另外也有学者将拉格朗日法、遗传算法及模拟退火算法应用于推力分配的优化，并在优化中通过目标函数及约束条件限制每个推进器的最大推力、推力变化及推进器方向角的变化[2-7]。动力定位系统中包含多个推进器，推力分配过程中，相邻推进器尾流相互干扰造成的推力损失可达45%以上，严重影响系统的定位性能和运行的经济性[8]。为了解决这个问题，文献[9-12]通过在推力禁区内设置推力衰减系数、在推力禁区内设置推力为零、使下游推进器的推力角始终位于推力禁区之外、设置动态推力可行域等方法，降低相邻推进器之间的水动力干涉，但这些方法会使推力可行域变为非凸集，无法直接使用序列二次规划法。

本文以某半潜式海洋钻井平台的动力定位系统为研究对象，使用基于严格等式约束的遗传算法将控制器的需求控制力和力矩分配给8 个全回转推进器，并依据环境扰动力方向的变化对目标函数进行简化。之后通过改进遗传算法，提高系统的运行速度及精度，并使用在推力禁区内设置推力减额系数的方法减低桨-桨干涉问题，最后通过仿真结果分析确定推力角的权值矩阵，并验证了所提方法的有效性。

1 动力定位的推力分配

动力定位系统配有8个全回转推进器，控制器通过比较平台当前状态与期望位置之间的差异，输出需求控制力及力矩，来抵消作用于平台的风、浪、流等环境载荷，而推力分配算法将控制力及力矩分配给8 个推进器，最后推进器通过控制转速达到期望推力，实现动力定位的功能，系统的具体工作流程如图1所示。

为了使所有推进器产生的合力及合力矩满足控制器的需求控制力和力矩，推进器的推力角和推力应满足

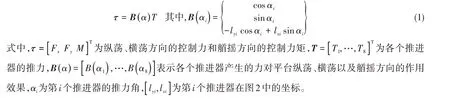
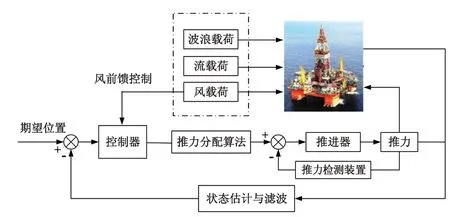
图1 动力定位系统的工作流程Fig.1 Workflow diagram of the dynamic positioning system

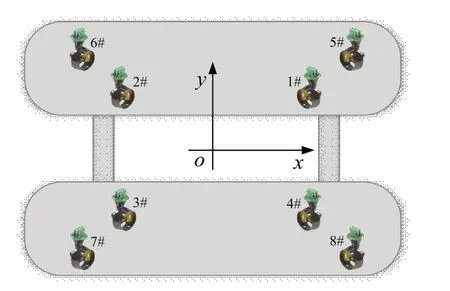
图2 推进器布置图Fig.2 Layout diagram of the thrusters

推力分配在满足控制器输出的需求控制力和力矩的同时，应该降低系统的燃油消耗，提高运行的经济性，系统的能耗功率可表示为

式中，KQ和KT分别为推进器的扭矩系数和推力系数，D为推进器直径，ρ为海水密度。

1.1 建立优化模型

通过8个全回转推进器来控制海洋钻井平台的3个自由度，属于过驱动控制问题。当控制器输出对横荡、纵荡方向上的合力及艏摇方向上的需求控制力矩时，需要对8 个推进器进行协同控制，在多种推力分配的结果中选取能耗最低、推进器磨损最小的一组。同时还要约束推进器所能提供的最大推力，全回转推进器推力角的变化速率、推进器之间水动力干涉以及避免系统奇异性等问题。因此得出推力分配的多目标优化函数为

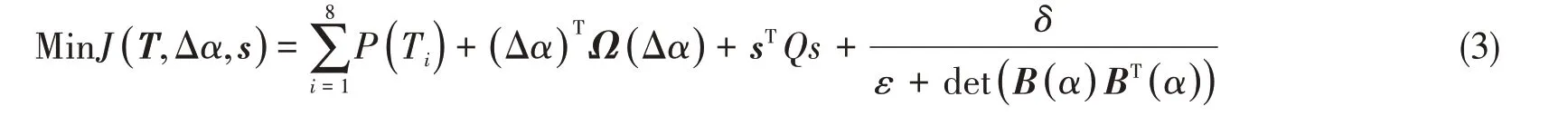
约束条件为

1.2 严格等式约束

式（3）中的目标函数通过对等式约束进行松弛，来解决等式约束的优化问题，但是松弛法会导致拓扑空间发生变化，使等式无法严格满足。本文采用文献[13]提出的基于降维和排序的约束遗传算法，来解决拥有等式约束的推力分配问题。经过降维处理的优化问题可以使等式约束严格满足，进而将约束条件全部转化为不等式约束。因为待优化的变量之间并不是独立的，假设待优化的变量有n个，而等式约束有m个，相当于有n-m个变量是相互独立的，另外m个变量可以通过解线性方程组，由剩余n-m个变量表达，进而在保证等式成立的前提下降低了变量数目。使用文献[12]中的需求控制力和力矩作为本文推力分配的输入，如图3所示。

从图3中横荡和纵荡需求控制力可以得出，需求控制力的方向变化缓慢，说明环境载荷的方向在一定角度内缓慢变化，因此系统发生奇异时并不会影响动力定位系统的操纵性及定位能力。

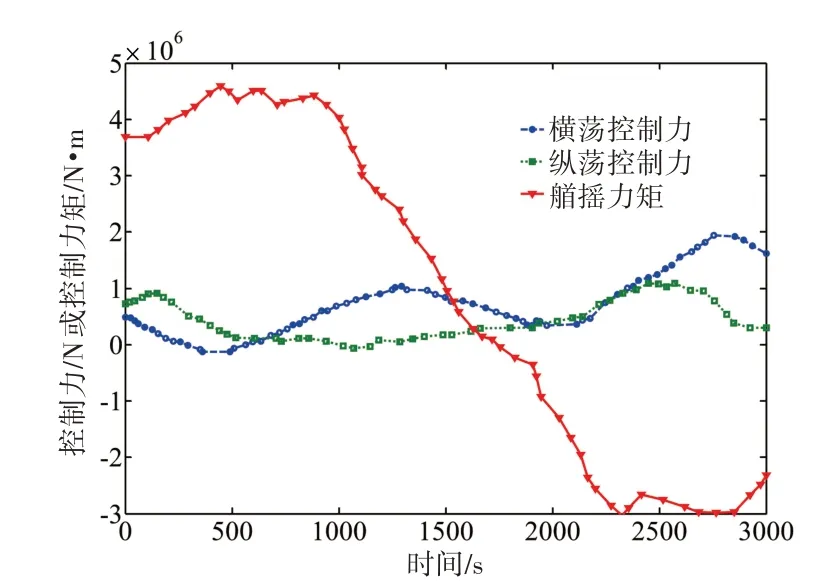
图3 需求控制力和力矩时程Fig.3 Time-history of control force and moment

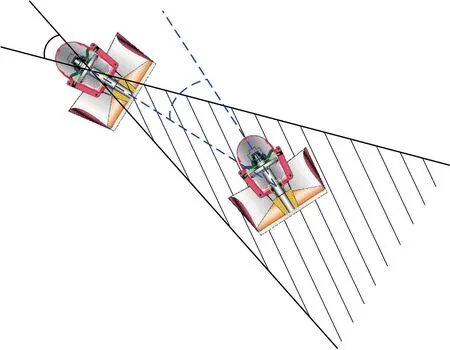
图4 桨-桨干涉示意图Fig.4 Sketch of thruster-thruster interference

综上所述，可将目标函数简化为

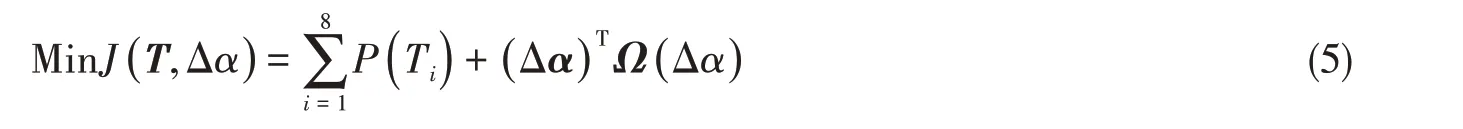
约束条件为

1.3 设置推力减额系数

位于上游的全回转推进器尾流会对处在同一直线上的下游推进器产生水动力干扰，使下游推进器的水流速度增大，导致推力减小，如图4所示。在推力分配的优化中，通常采用设置推力禁区、推力衰减、在推力禁区内限制最大推力等方法来避免或减小全回转推进器的水动力干扰问题。但设置推力禁区或者在推力禁区内限制前一个推进器的最大推力可能会降低优化效果，因此采用在推力禁区内设置推力减额系数的方法。推力减额系数与推进器的推力大小以及方向有关，前一个推进器的推力越大，则后一个推进器受水动力干扰的影响就越大，两个推进器在x轴方向上的重叠角度越大，则影响越大。Dang等[14]研究了推进器间距和推力夹角对推力损失的影响，并总结得出了关于桨-桨干涉导致推力损失的经验公式。推进器前后布置，推进器间距变化时推力减额系数的表达式为

式中，t 为推力减额系数，Tu为下游推进器的推力，T0为敞水系柱下推进器的推力，x 为推进器的间距。当推进器的间距固定，推进器夹角变化时导致的推力损失可表示为

式中，Φ为两推进器之间的推力夹角，t为x/D=定值、Φ = 0时的推力减额系数。

2 改进遗传算法

遗传算法具有很强的全局搜索能力及很好的鲁棒性能，适用于求解推力分配这种超静定约束的优化问题。但是标准遗传算法的局部搜索能力较弱，并且后期由于个体间的高相似度会导致种群停止进化。本章以满足严格等式约束的算法为基础，从两个方面对标准遗传算法进行改进来提高其优化速度及精度：一是采用基于上一时刻精英个体的均匀分布种群生成方法（改进遗传算法1）；二是在标准遗传算法中结合自适应算法（改进遗传算法2）。

2.1 初始种群的生成方法

遗传算法的时效性很大一部分取决于初始种群的精英程度。一般来讲，初始种群如果拥有较高的精度和多样性时，遗传算法的搜索效率及收敛速度能够得到很大的提升。但标准遗传算法的初始种群是随机生成的，无法保证其精英程度及多样性。在推力分配的目标函数中，存在着对推进器推力及推力角的约束，这就导致下一时刻的推力及推力角的取值范围必须在上一刻推力及推力角最优值的附近。本文采用遗传算法的种群数目设为p，将上一时刻适应度最高的q（q＜p）个个体作为下一时刻初始种群的一部分，每个个体由n个变量组成。设Ui是初始种群的第i个个体，uij是Ui的第j个变量，则

另外p-q个初始种群个体采用随机分布的方法生成，其变量可表示为

式中，ζ表示在[0,1]内的随机数，aj和bj分别是变量uij的下限和上限，i=q+1,q+2,…,p，j=1,2,…,n。

2.2 自适应局部搜索算法

遗传算法的性能好坏很大程度上取决于交叉算子和变异算子。交叉算子的作用是生成新的个体，对遗传算法的全局搜索能力具有很大影响；而变异算子只是用来辅助生成新个体，但它能改变个体编码串的结构，维持种群的多样性，防止早熟现象的出现，并对遗传算法的局部搜索具有很大影响。标准遗传算法随着进化代数的增加，种群的个体相似度会越来越大，交叉算子很难产生新的个体，这时应该动态调整交叉和变异算子，增大变异概率，减小交叉概率。所以本文使用结合自适应调整交叉和变异算子的算法来提高遗传算法的局部搜索能力，进而提高推力分配的优化精度。

在进化中，以适应度的变化来改变交叉和变异的概率。设群体的最佳适应值为gmax，当代最佳的适应值为fmax，当代的平均适应值为favg；设定两个交叉概率和两个变异概率，分别为Pcmax、Pcmin和Pmmax、Pmmin。则具体的算法为

if g＞k

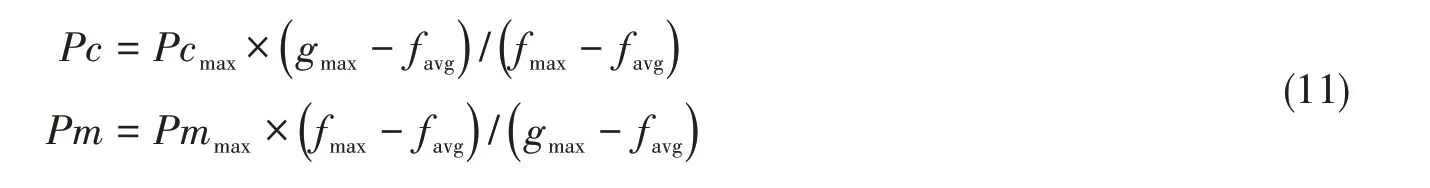
otherwise

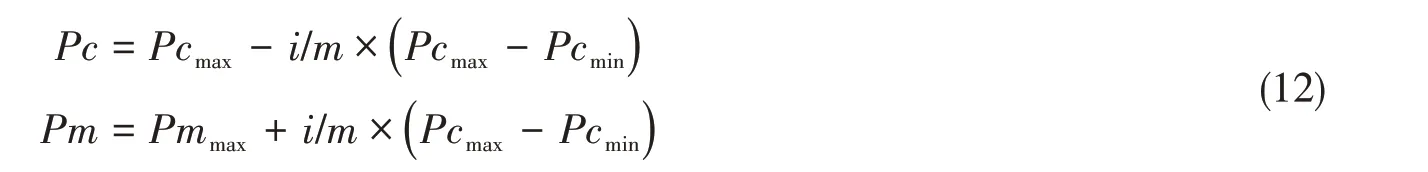
式中，g是fmax与gmax的比值，k是设定的阈值，i是进化代数，m是总的进化代数。

3 仿真结果及分析

以某半潜式海洋钻井平台为研究对象，其参数如表1所示。推进器选用文献[15]给出的W-B4-70型导管螺旋桨，其推进功率为4 600 kW，系柱状态下推力系数KT=0.445，扭矩系数KQ=0.06，直径D=4 m，Tmax=540 kN，Tmin=0 kN，螺旋桨转速变化率为±0.2 s-2，则推力变化率范围为ΔT=±4.67 kN/s，转角变化率范围为Δα=±1°/s。为增大相邻推进器的间距，降低水动力干涉问题，将每组推进器进行错位安置，如图2所示。当推进器在系柱状态下距离上游推进器3倍直径时，其尾流速度分布为沿轴线向两侧逐渐减小，尾流的影响范围约为推进器的2倍直径[16]。因此本文取θ=36°，所有推进器的位置坐标及推力衰减界限如表2所示。

海洋钻井平台的动力定位系统配备有8台全回转推进器，目标函数的自变量有16个，但经过降维处理，6～8号推进器的推力可由其他变量表示，所以目标函数的最终自变量为13个。遗传算法的最大进化代数为200，种群数量为100，将上一时刻最优的20个个体作为下一时刻初始种群的一部分。k为0.9，Pcmax为0.8，Pcmin为0.6，Pmmax为0.04，Pmmin为0.02，自变量离散精度eps为0.1。

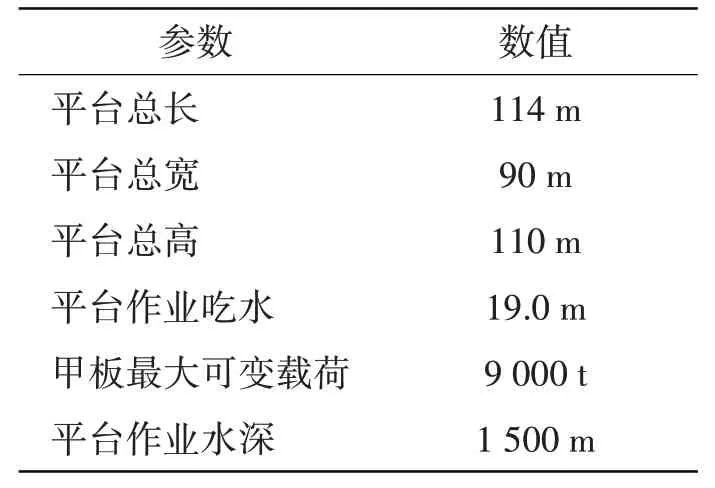
表1 某海洋钻井平台参数Tab.1 Parameter of an offshore drilling platform

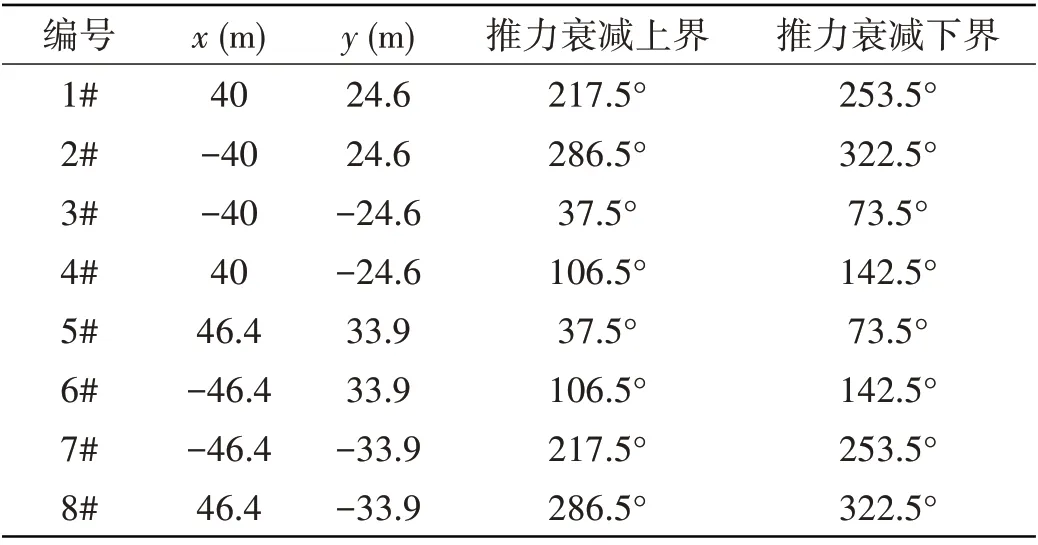
表2 推进器参数Tab.2 Thruster parameters

3.1 权值矩阵的确定

因为简化后的目标函数共有两项，即动力定位系统既要降低能源消耗，提高运行的经济性，又要减小推进器的磨损。设推力角的权值矩阵Ω =K×I8×8，比较单位采样时间内，不同K值下推进器的平均转动夹角和总功率消耗之间的差异，分别如图5和图6所示。

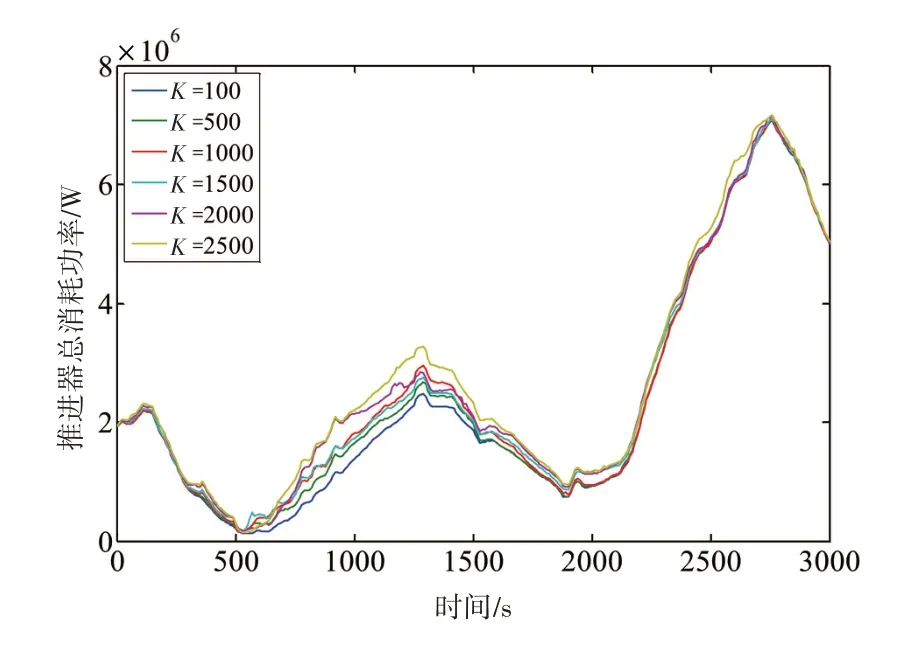
图5 权值矩阵对推进器能耗的影响Fig.5 Influence of weight matrix on thruster energy consumption

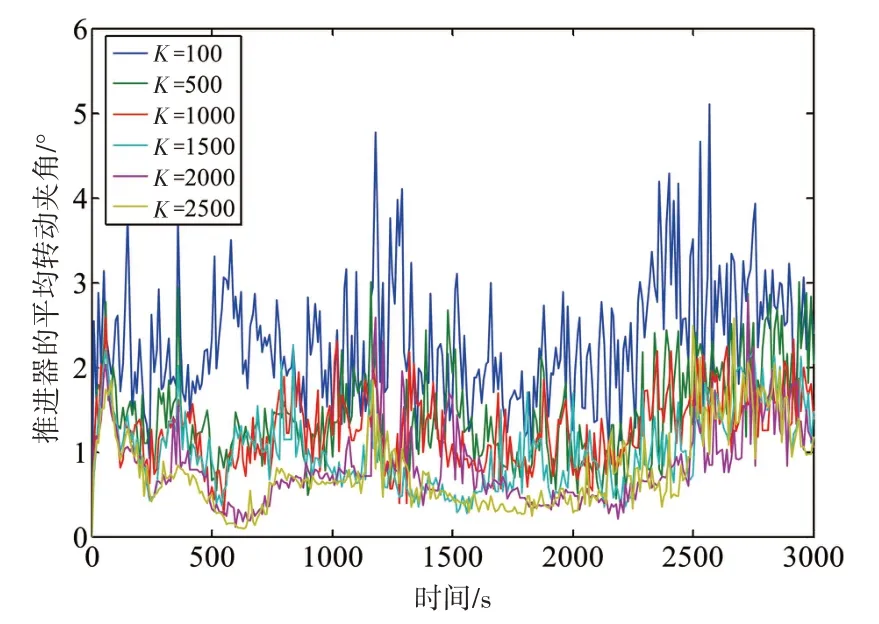
图6 权值矩阵对推进器磨损的影响Fig.6 Influence of weight matrix on thruster abrasion

表3 K值对推进器能耗和磨损的影响Tab.3 Effect of K-value on propeller energy consumption and abrasion

从图5 和图6 中可以看出，随着K 值的增大，动力定位系统的能耗增加，而推进器的磨损减小，因此两者存在一定的冲突关系，需要选择一个折中方案，确定权值矩阵的大小。计算得出不同K值下推进器能耗和磨损在整个时域内的平均值，如表3所示。

基于此，本文选取K=1 500，即Ω =1 500×I8×8。

3.2 改进遗传算法的效果

为了验证改进遗传算法的有效性，取图3 第20 s 时的需求控制力及力矩作为输入，比较改进遗传算法和标准遗传算法在优化进程方面的差异，如图7所示。之后将图3在整个时程内的需求控制力及力矩作为输入，继续研究改进遗传算法对优化结果的影响，优化结果如图8 所示。其中图7 和图8 中的数据为多次仿真实验的平均值。

从图7中可以看出，改进遗传算法1的初始种群精英程度明显高于改进遗传算法2和标准遗传算法，且前期收敛速度快；而改进遗传算法2 的最终收敛精度高于改进遗传算法1 和标准遗传算法。另外从图7 中可以得出，改进遗传算法2 的优化效果最好，通过统计三种算法在整个时程内目标函数的平均值，发现改进遗传算法1 的优化结果比标准遗传算法高0.81%，改进遗传算法2 的优化结果比标准遗传算法高3.09%。

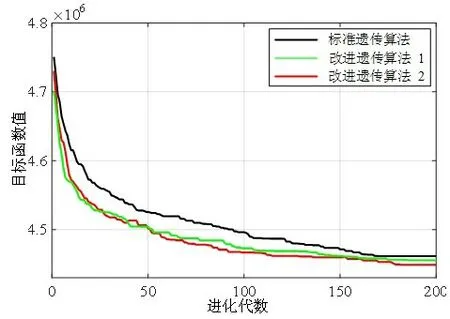
图7 改进遗传算法对优化进程的影响Fig.7 Influence of improved GA on the optimization process

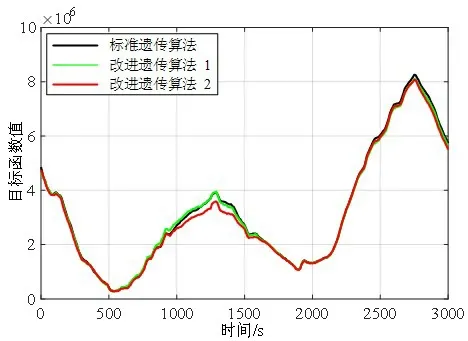
图8 改进遗传算法对优化结果的影响Fig.8 Influence of improved GA on the optimization results

3.3 推进器推力角和推力的时程变化

定义#1～#4 推进器的初始推力角分别为30°、150°、210°、330°，#5～#8 推进器的初始推力角分别为60°、120°、240°、300°。将建立的推力分配模型导入改进的遗传算法中，得出推力角和推力的分配结果如图9所示，单位采样时间内推力角和推力的变化如图10所示。其中，图9中阴影部分为上游推进器对下游推进器造成推力损失的区域。

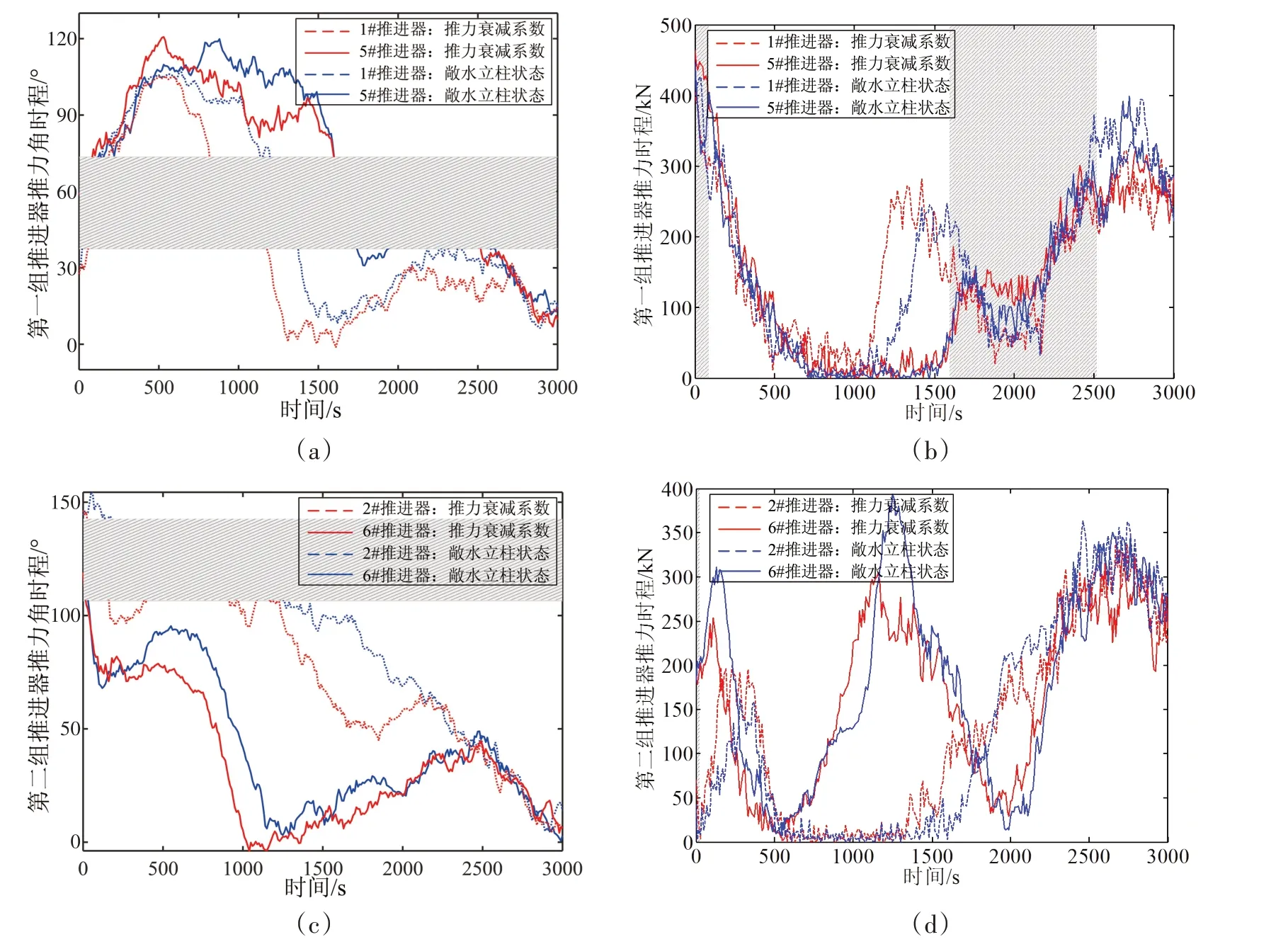
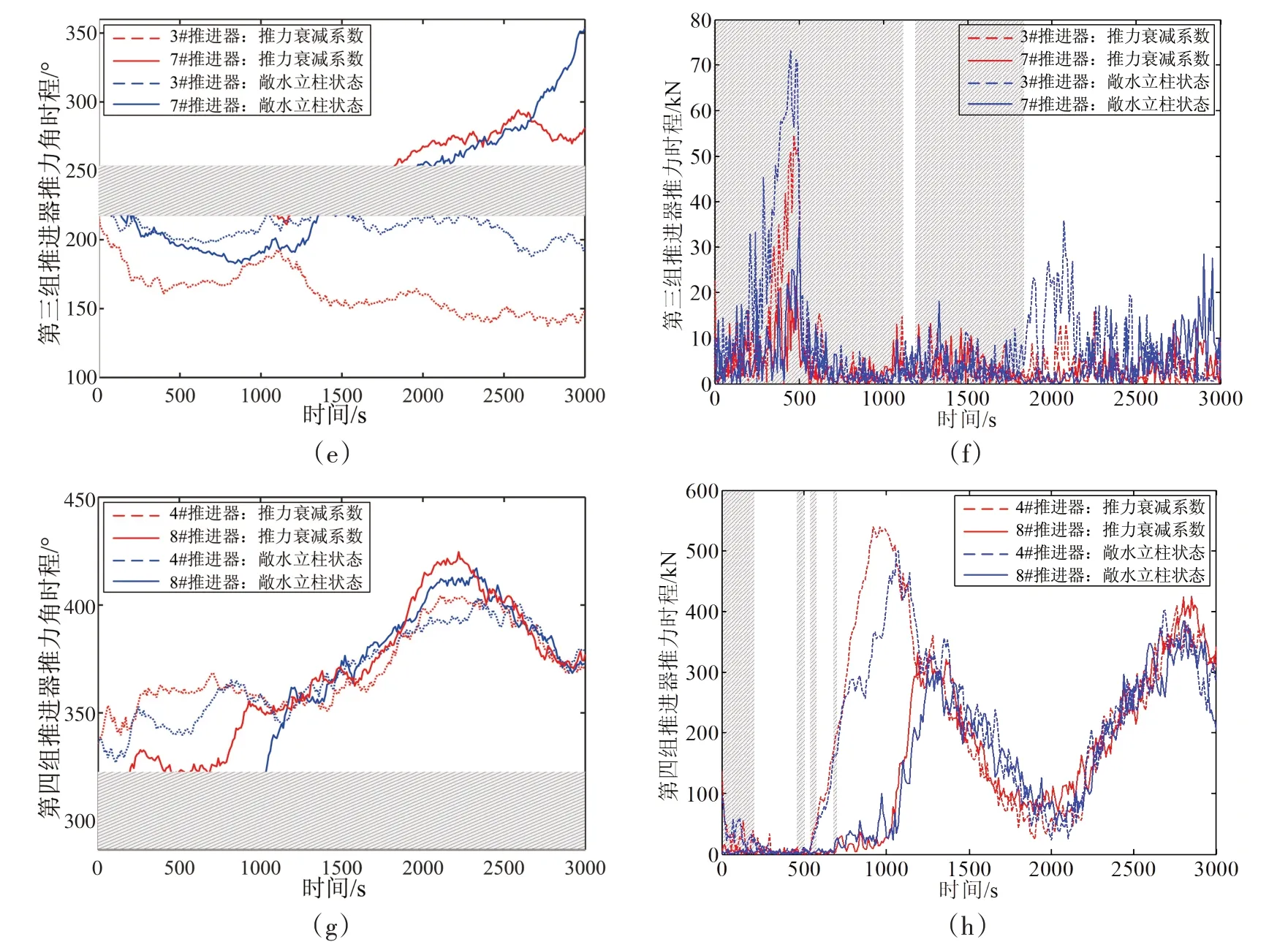
图9 推进器推力和推力角的时程变化Fig.9 Time-history variation of the thrust and thrust angle

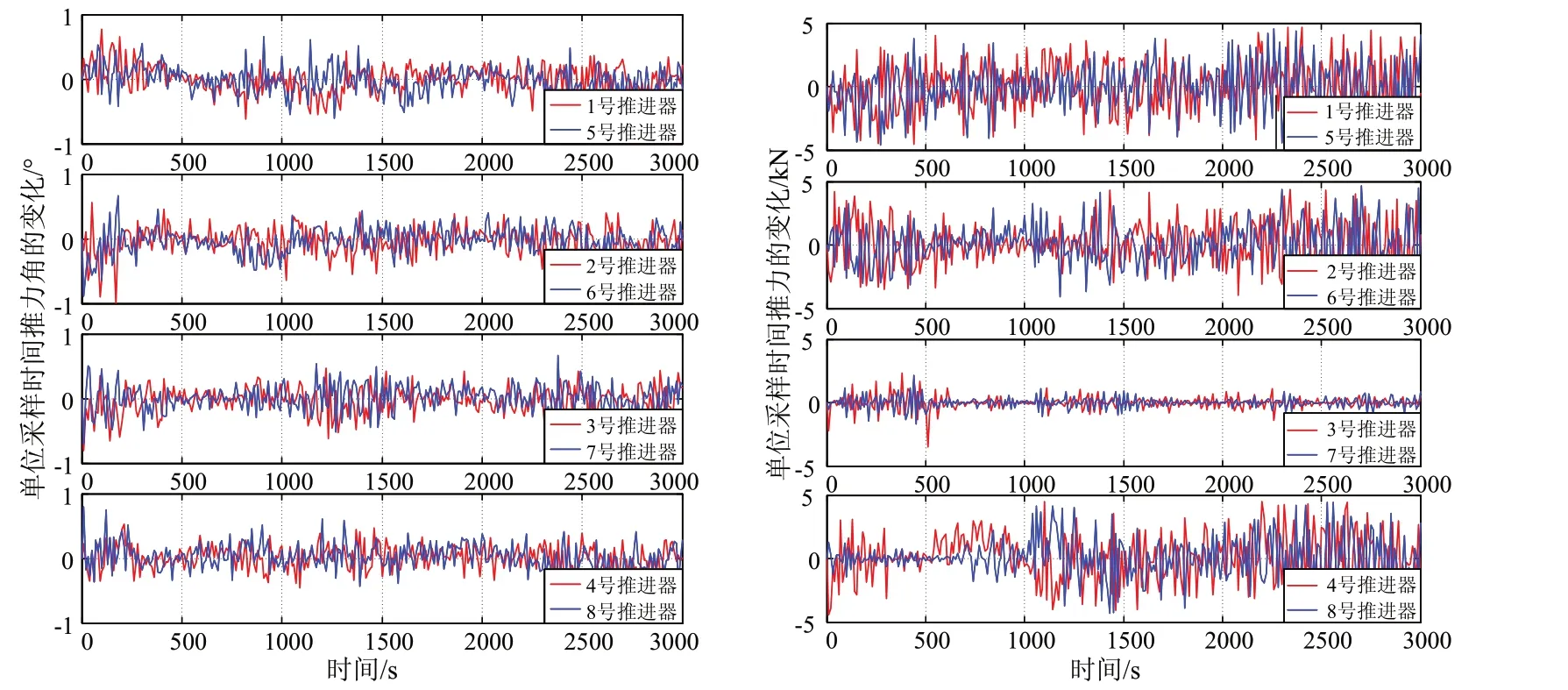
图10 单位采样时间推力角和推力的变化Fig.10 Thrust angle and thrust change during each unit sampling time

图9（a）和图9（b）分别表示第一组推进器推力角和推力的时程变化，当#5推进器推力角位于阴影区域作为上游推进器对#1 推进器造成水动力干涉时，相比于敞水立柱状态，#1 和#5 推进器之间的推力夹角Φ 会增大，且#1 推进器的推力会减小，从而降低推力损失。图9（c）和图9（d）分别表示第二组推进器推力角和推力的时程变化，#6推进器作为上游推进器仅仅在开始的极短时间内位于阴影区域，并没有对#2推进器造成水动力影响。图9（e）和图9（f）分别表示第三组推进器推力角和推力的时程变化，与第一组推进器类似，相比于敞水立柱状态，#7 推进器推力角位于阴影部分时会使两推进器之间的推力夹角Φ 增大，且#3推进器的推力减小，从而降低推力损失，另外#3和#7推进器的推力在整个时程内都很小，说明这组推进器的推力角与环境扰动方向大致相同。图9（g）和图9（h）分别表示第四组推进器推力角和推力的时程变化，当#8 推进器推力角位于阴影部分时，#4 和#8 推进器之间的推力夹角Φ并没有增大，这是因为此时#8推进器作为上游推进器的推力非常小，基本不会对下游推进器造成推力损失。

从图10中可以看出，单位采样时间内，推进器的转动夹角较小，说明推力角的权值矩阵选取得当，推进器的磨损较小。另外，单位采样时间内推力变化未超过±4.67 kN/s，转动夹角变化未超过±1°/s，符合式（6）给出的推力及推力角的约束条件。

4 结 论

本文提出了一种基于严格等式约束的改进遗传算法对海洋平台进行推力分配的优化。该方法解决了优化算法对等式约束的求解问题，并具有较高的优化速度及收敛精度。在简化目标函数的基础上建立了最优推力分配模型，并通过仿真得出一些结论：

（1）在标准遗传算法的基础上，采用继承上一时刻精英个体的初始种群生成方法，能够提高初始种群的精英程度和算法的收敛速度；自适应交叉和变异算子能够提高优化结果。

（2）随着推力角权值矩阵的增大，动力定位系统的能耗会增加，而推进器的磨损会减小，因此两者存在一定的冲突关系，需要选择一个折中方案，确定权值矩阵的大小。

（3）针对设置推力减额系数的方法，当下游推进器位于上游推进器的推力衰减区域时，相比于敞水立柱状态，两推进器的推力夹角会增大，且下游推进器的推力会降低，说明该方法能在一定程度上避免推力衰减，提高系统运行的经济性。通过对比结果表明，该方法在解决推力分配的优化问题上是有效的。