转捩模型在螺旋桨数值计算中的应用
洪方文,张志荣,刘登成,郑巢生,翟树成
(1.中国船舶科学研究中心,江苏无锡214082;2.船舶振动噪声重点实验室,江苏无锡214082)
0 引 言
自计算机诞生以来,数值计算成为科学研究的一种主要手段。在流体力学领域中,经过七十年的发展,计算流体力学(CFD)已经成为船舶流动分析的主要工具。船舶螺旋桨CFD 已经被广泛应用于推进器设计中,使得设计目标实现的确定性大为提高。通过广泛使用发现,大部分情况下螺旋桨敞水性能CFD预报的精度误差都能达到不超过3%的水平,满足螺旋桨设计的工程需要。不过同样也会出现预报精度很差的情况,甚至误差会达到20%的状况,这说明螺旋桨设计中CFD的应用还存在一定的技术风险,进一步完善船舶CFD技术,提高其计算精度是一项重要的工作。
数值求解螺旋桨流动问题始于20 世纪80 年代,最初针对非湍流控制方程、有势流方程[1]和Euler方程[2]、低马赫数可以压缩流动N-S 方程[3-5]及不可压缩层流N-S 方程[6-7]进行求解。90 年代初期开始出现了求解不可压缩RANS方程的螺旋桨湍流流场CFD计算[8-10],使得计算精度有了很大的提高。在90 年代中期螺旋桨的定常流计算已相当广泛,并应用到螺旋桨水动力性能的预报中[11-13]。到90 年代末期,螺旋桨CFD 已经比较成熟,可以较好地预报螺旋桨敞水性能。1998 年,第22 届ITTC 推进技术委员会在法国Grenoble 专门举行了RANS/面元法螺旋桨性能比较计算研讨会[14-16],研讨会的主要结论是RANS 和面元法都可精确地预报螺旋桨的敞水性能,能够用于螺旋桨设计阶段的性能预报。进入本世纪后,CFD 已经广泛应用到螺旋桨的精细流动模拟和性能分析上[17-20]。现在求解RANS的CFD 虽然已被广泛用于螺旋桨水动力性能计算和流动模拟,但总是存在一些不足的地方。水动力计算中在重负荷的情况下误差变大,虽然雷诺数增加计算误差有减小的趋势[21-23],但仍会出现不可接受的水平。在梢涡和毂涡的计算中,涡心尺寸和速度耗散总是偏大[24-27]。
出现这些现象,主要是由于螺旋桨叶片的流动状态没有得到正确的模拟。RANS方法一般把流动作为全湍流进行模拟,然而对于模型螺旋桨流动,由于雷诺数在105量级,在桨叶上还存在较大面积的层流状态[28],需要使用具有转捩能力的湍流模型进行模拟[23,29-31]。在本研究中将利用具有转捩能力的湍流模型计算螺旋桨模型流动,分析其计算螺旋桨水动力特性的精度。
1 数值方法
1.1 控制方程
控制方程使用旋转坐标系下不可压缩流体雷诺平均质量和动量守恒方程:

1.2 数值求解
流动的数值求解使用商用软件FLUENT,该软件对控制方程的离散使用有限体积法。动量守恒方程和湍流方程中的对流项离散使用二阶迎风格式,扩散项使用二阶中心差分格式,流场中物理量梯度计算使用基于单元的Green-Gauss 方法。离散方程求解利用SIMPLE 方法和Gauss-Seidel 迭代,同时求解过程中使用多重网格技术加速迭代的收敛。压力计算松驰因子取0.3,速度计算松驰因子取0.7,湍流计算松驰因子取0.8。计算中各方程的收敛条件为10-4,但整个计算过程的收敛通过螺旋桨的推力系数变化来判断,当螺旋桨推力系数变化小于10-3时,可认为计算过程收敛,结束计算。
1.3 初始边界条件
在旋转坐标系下,假设流动具有与螺旋桨叶片数相同的周期性,计算区域取一个流道的扇形区域。进口在螺旋桨前方6D处,出口在螺旋桨后方10D处,区域半径为6D,D是螺旋桨的直径。为了划分高质量的网格,把计算区域划分为6块子区域,子区域形式显示在辐射面内,如图1所示。
计算区域边界包含进口边界、出口边界、顶部圆周边界、螺旋桨叶片、桨毂、前轴、后轴和周期边界。进口边界和顶部圆周边界施加速度进口边界条件,设定进口速度和湍流相关参数;出口边界施加压力边界条件,给定出口压力;螺旋桨叶片和桨毂使用不可滑移物面边界条件;前轴和后轴使用滑移物面边界条件;周期边界施加周期边界条件;计算的速度初始条件使用绝对坐标下的来流均匀速度。
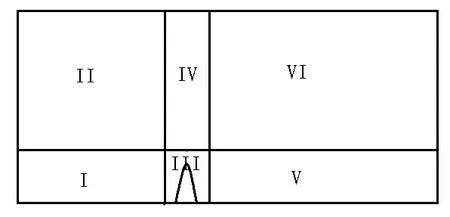
图1 计算区域划分形式示意Fig.1 Division of computing domains
2 对象和网格
研究对象选为28 000 DWT多用途船的螺旋桨模型,其主参数如表1所示。
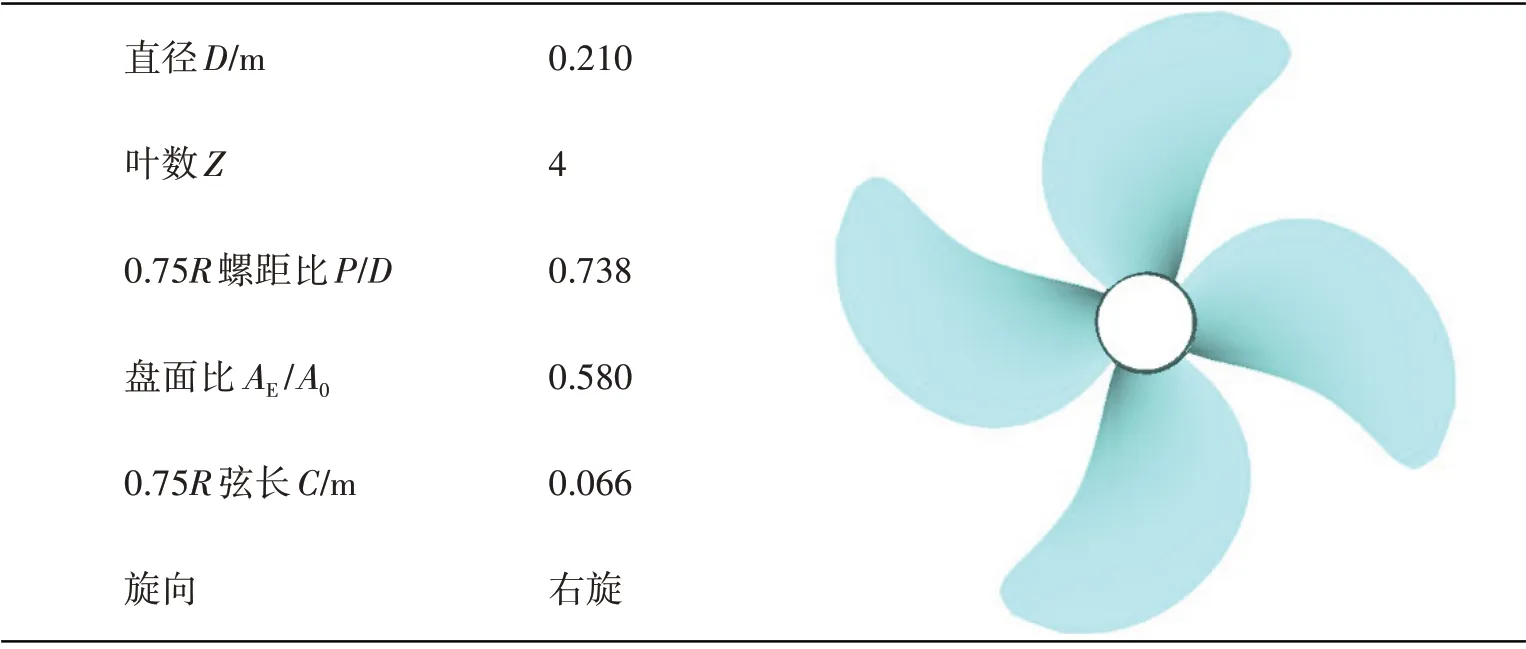
表1 螺旋桨模型主参数Tab.1 Main parameters of propeller model
在计算域内,包含螺旋桨的区域使用非结构化网格,其他区域使用结构化网格。螺旋桨叶片导随边网格加密,导随边网格尺度以1%D 为基础变化,叶片上的网格形式如图2所示。叶片附近网格以螺旋桨叶片上的网格尺寸为基础,向外以1.1的比例增长;在螺旋桨的进口区域,轴向布置15 个网格,进口处尺寸为1.0D,与螺旋桨区域交接处网格尺寸为6%D;在螺旋桨的出口区域,轴向布置20个网格,出口处尺寸为1.0D,与螺旋桨区域交接处为6%D,径向使用15个网格;在顶面处尺寸为1.0D,与螺旋桨区域交接处网格尺寸为12%D,周向均匀布置39 个网格;螺旋桨的前后区域使用桶型平推网格。在研究中将以这里描述的网格为基础进行加密和稀疏。

图2 螺旋桨叶片上的网格形式Fig.2 Meshes on the propeller blade
3 结果和分析
计算中进口速度V=1.782 45 m/s,螺旋桨转速N=17 r/s,螺旋桨进速系数J=0.5,计算中参考压力为一个大气压,出口相对压力设为0.0。分别利用SST k-ω湍流模型和γ - R͂eθ转捩模型,以及4套网格进行计算,计算结果如表2和表3所示。KT和10KQ的试验结果为0.149 1和0.192 0。从表中可以看出,对于SST k-ω 模型,KQ的计算误差很小,并且不同的网格数得到的计算结果很稳定,但KT的计算误差较大,随网格数的增加,呈增大和发散趋势。γ - R͂eθ模式计算得到的误差,KT和KQ都在一个较好的水平,并且随网格数的变化稳定性较好。
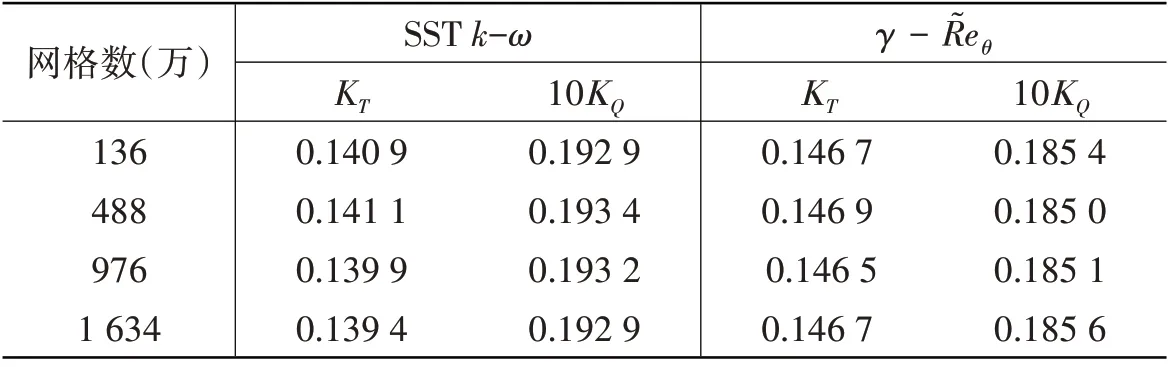
表2 KT和KQ计算结果Tab.2 Calculating results of KT and KQ
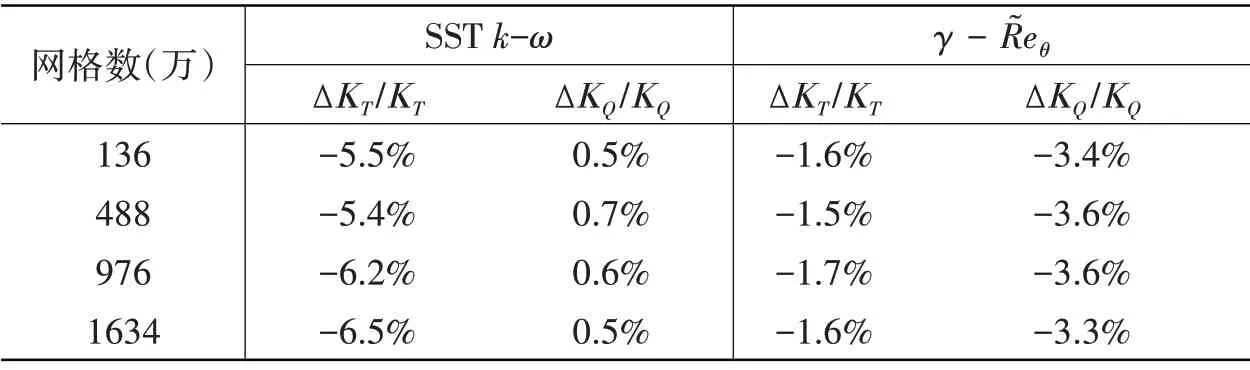
表3 KT和KQ计算误差Tab.3 Calculating error of KT and KQ
计算显示,使用带有转捩的湍流模型计算结果与试验更为吻合,这说明桨叶表面有很大的区域保持着层流状态。在RANS 方法中,默认物体表面流动全处于湍流状态,而实际中物体表面起始流动总是处于层流状态,湍流是随着层流的发展转捩后形成的。在流动雷诺数很高时,物面开始的层流区域较小,绝大部分区域都处于湍流状态,对于RANS 方法中默认引起的误差是很小的。在流动雷诺数较小的情况,层流区域占有物面相当的比例,如果全部当作湍流处理,可能会引起较大的误差。本文计算对象在17 r/s 的转速下0.7R 处的流动雷诺数为3.4×105。一般情况下,对于物面的临界雷诺数为2.0×105-6.0×105。这样看来,桨叶表面可能还有50%的区域处于层流状态。图3给出了两种湍流模式计算的桨叶表面流态,同时给出了另一螺旋桨的试验结果。从流态看非转捩模型计算的结果,压力面分离区较小,且吸力面和压力面沿半径方向的流动更明显,呈现湍流的流动特性。转捩模型计算的结果与试验结果更相似,在吸力面有较大的分离区,吸力面和压力面径向流动更明显,呈现层流的流动特性,这与试验结果一致。在数值模拟时,如果使用全湍流模式将对计算结果有较大的影响。
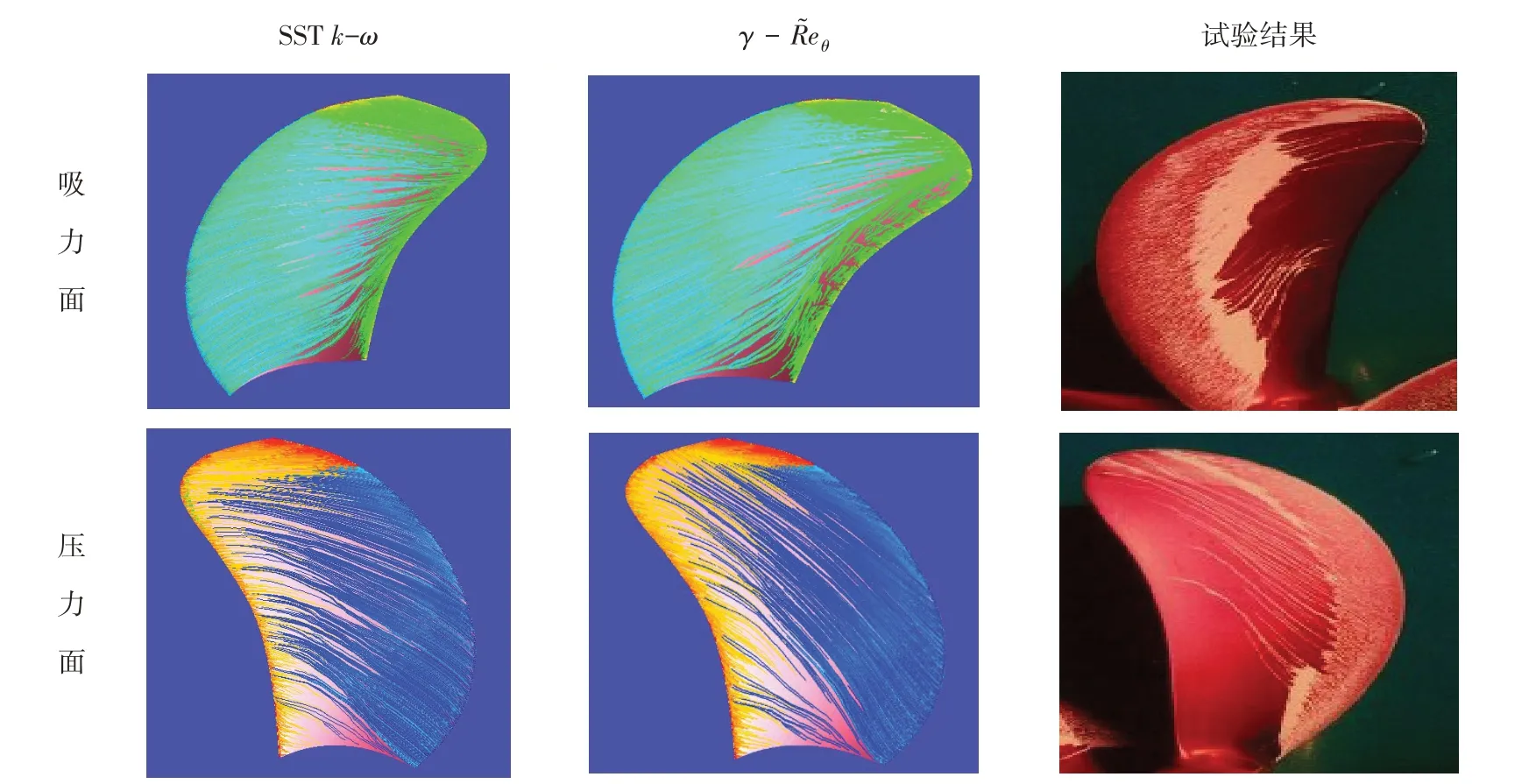
图3 桨叶表面流动状态Fig.3 Flow traces on blade surface
转捩湍流模型应有更宽的适用范围,它既可以处理层流占比大的问题,也可以处理层流占比小的流动问题,也就预示着在高雷诺数时,转捩湍流模型计算结果将与非转捩湍流模型一致,以及在低雷诺数时,对于不同的对象,其计算结果的精度都将得到改善。表4 列出了雷诺数提高10倍的计算结果,可以看出在高雷诺数的情况下两种湍流模式计算的螺旋桨水动力系数相差很小,在0.1%以内。表5 给出了另外4 个算例的计算误差,从表中可以看出,使用转捩湍流模型计算结果的精度都得到了不同程度的改善,说明转捩湍流模型具有更宽的适用范围。
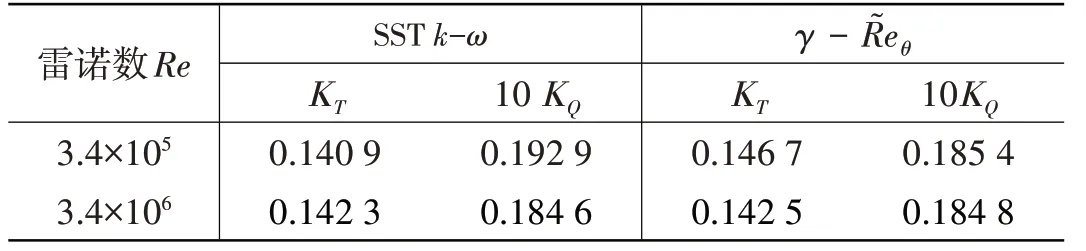
表4 不同雷诺数计算结果Tab.4 Calculating results of KT and KQ at different Re numbers
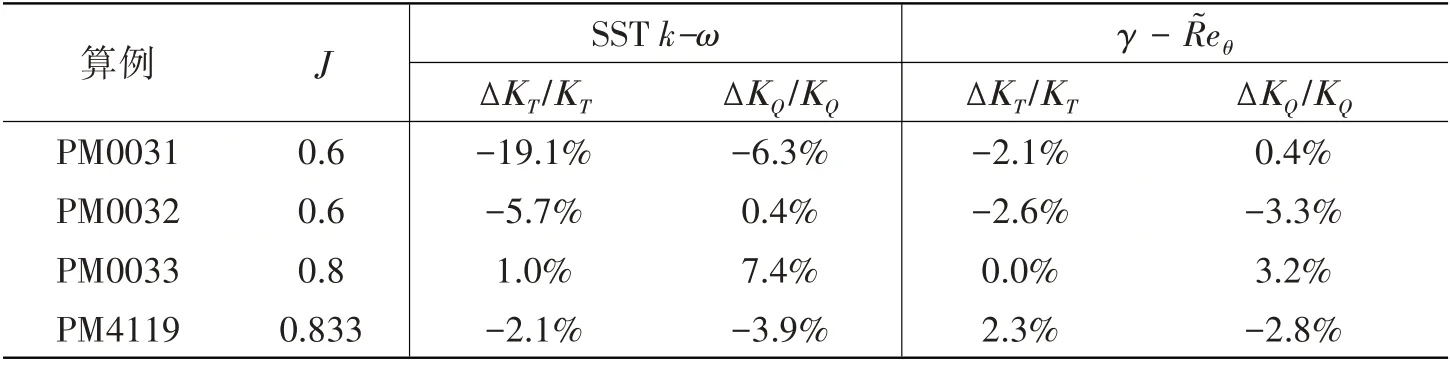
表5 系列算例的计算结果误差Tab.5 Calculating errors of KT and KQ for a few propellers
4 结 语
在模型试验中,螺旋桨叶片流动雷诺数Re=5.0×105左右,虽然已经大于相关试验规程中要求的临界雷诺数,但螺旋桨叶片表面仍然有相当区域的流动为层流状态。一般情况下,螺旋桨模型敞水的流动计算都使用基于雷诺平均方程的湍流模式,即把螺旋桨叶片表面的流动全部作为湍流处理。但作为全湍流处理,并不符合实际的流动情况,所以计算结果有时会出现较大的偏差,必须使用带转捩的湍流模式进行螺旋桨模型的敞水流动计算,才能保证计算精度。

