移动机器人路径规划的改进蚁群算法

张 仪 赵苗慧 杨 兵 张 彤

（陕西省可控中子源工程技术研究中心，西京学院理学院，陕西 西安710123）

近年来，由于人工智能的飞速发展，移动机器人的发展也成为人们讨论的热点，同时路径规划是移动机器人主要讨论的焦点。路径规划是指移动机器人在有障碍的环境中寻找一条无碰撞的路径[1]。路径规划的智能优化算法主要有：遗传算法、模拟退火算法、粒子群算法、免疫算法等。这些算法在移动机器人路径规划时能取得很好的结果，但面对复杂环境时依然存在一定的缺陷[2]。

本文将改进的蚁群算法是一种启发式的随机搜索算法。蚁群算法来源于自然界蚂蚁寻找食物的过程。该算法主要模拟蚂蚁群体觅食的过程，蚂蚁在寻找食物的过程中，会在所经过的路径上留下信息素，而在找到食物，且路程较短的路径上留下较多的信息素，这也给后来寻找食物的蚂蚁提供了强有力的方向指引，更多的蚂蚁会往信息素浓度高的路径上走[3]。但传统的蚁群算法存在收敛速度慢、容易陷入局部最优解等问题[4]。本文将根据传统蚁群算法所存在的问题提出一种改进蚁群算法。

1 障碍物模型建立

本文将利用栅格法来模拟障碍物环境，黑格表示障碍物，在矩阵中由1 表示，白格表示可行空间，在矩阵中由0 表示。栅格点标号依据从左到右，从上到下的顺序依次标号。每个标号代表一个栅格点。每个栅格长度定义为1。坐标原点定义为左上点。并建立XOY 坐标系。坐标点（X,Y）和栅格标号G 对应的关系为式（1）和式（2）所示：

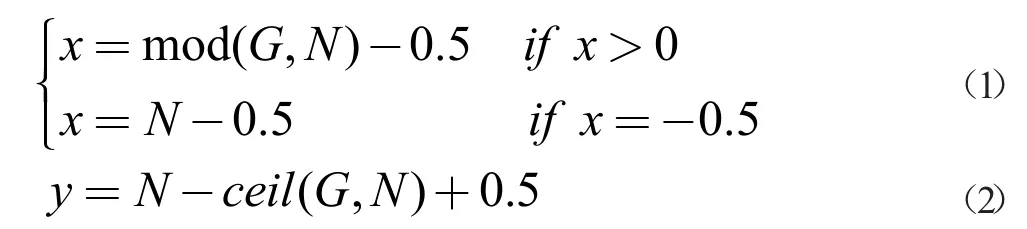
式中，G 是栅格点标号，N 是矩阵的行列数，mod 是进行取余数操作，ceil 是进行朝正向元素方向取整操作。对移动机器人在栅格中的移动规定以下准则:（1）移动机器人只能在白格中移动，并将移动机器人作为质点。（2）移动机器人每次从每个栅格的中心出发，每次只能向周围八个中心移动，每次移动的距离为1 或1.414。向上下左右移动时的距离为1，向左上、左下、右上、右下移动时距离为1.414。

2 蚁群算法

2.1 传统蚁群算法

2.2 传统蚁群算法的不足

2.2.1 迭代次数多。传统蚁群算法在前期迭代时，每条路径上的信息素浓度差别不大，就加大了蚂蚁寻找最优路径的范围，需要更多的时间去搜索路径，直到找到最优路径。

2.2.2 易陷入局部最优解。传统蚁群算法寻找到较优路径时，就会往这条路径上释放更多的信息素，从而引来更多的蚂蚁在这条路径上留下信息素，通过正反馈，令较优解成为了最佳路径。

2.2.3 参数的大小选择影响算法寻优能力。参数的选择直接影响算法的寻优能力，参数选择不当直接影响算法的可行性。

2.3 改进蚁群算法

通过上述分析的不足，对蚁群算法提出以下改进：

2.3.1 解决陷入U 型陷阱问题。当蚂蚁陷入U 型陷阱时，蚂蚁只能选择回退，但上一个节点已经无法回退，此蚂蚁就陷入了锁死状态。文献[5]就提出将锁死的蚂蚁丢弃。但此方法并未将蚂蚁陷入锁死时的节点加入禁忌表，没有为后来出发的蚂蚁留下有效信息。本文提出一种新的解决方案，当蚂蚁陷入锁死时，将此节点加入禁忌表中，并将此蚂蚁之前路径上的信息素清零，再令此蚂蚁从起始点重新出发。

2.3.2 设计自适应信息素挥发因子ρ。信息素挥发因子ρ 的大小影响着蚁群算法的收敛速度，也影响算法能否找到最优路径。当ρ 过大时，容易导致信息素挥发过快，减少了较优路径上的信息素含量，从而导致最优路径可能被排除。当ρ 过小时，会使各路径上信息素含量差别不大，从而导致最优路径不容易被选择，影响算法的收敛性。本文设计了一种自适应信息素挥发因子。本设计引入Sigmoid 函数作为信息素挥发因子前面的系数。本设计只引入Sigmoid 函数大于0 的部分。改进如式（3）所示。

式中，ρ 和N 为程序初始化设定的参数，信息素挥发因子和迭代次数，Nn为进行到第n 次的迭代。

若取N 为100，则ρ 前面的系数值与迭代次数N 的曲线关系如图1 所示。

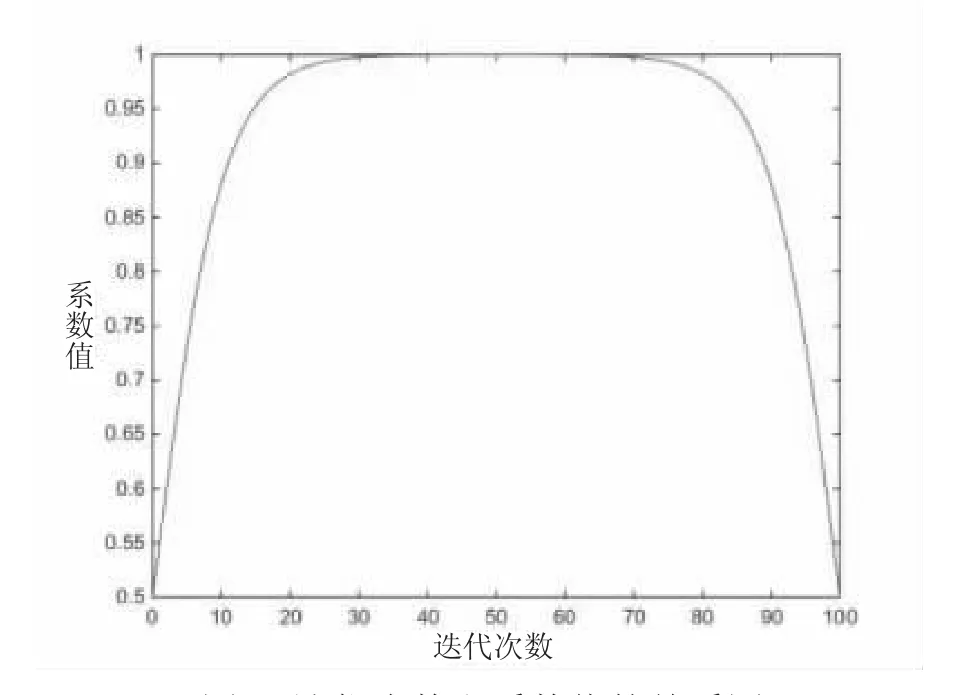
图1 迭代次数和系数值的关系图

由图1 可知该式实现了ρ 的大小随迭代次数变化而变化的效果。在迭代初期和末期，ρ 的取值最小，初期时，取值越小有利于蚂蚁更容易找见最优路劲，末期时，取值越小有利于增快收敛性。当中期取值较大时，能增大信息素的挥发，若陷入局部最优解，就更容易找到更优的解，使蚂蚁避免陷入局部最优解。

3 实验结果与分析

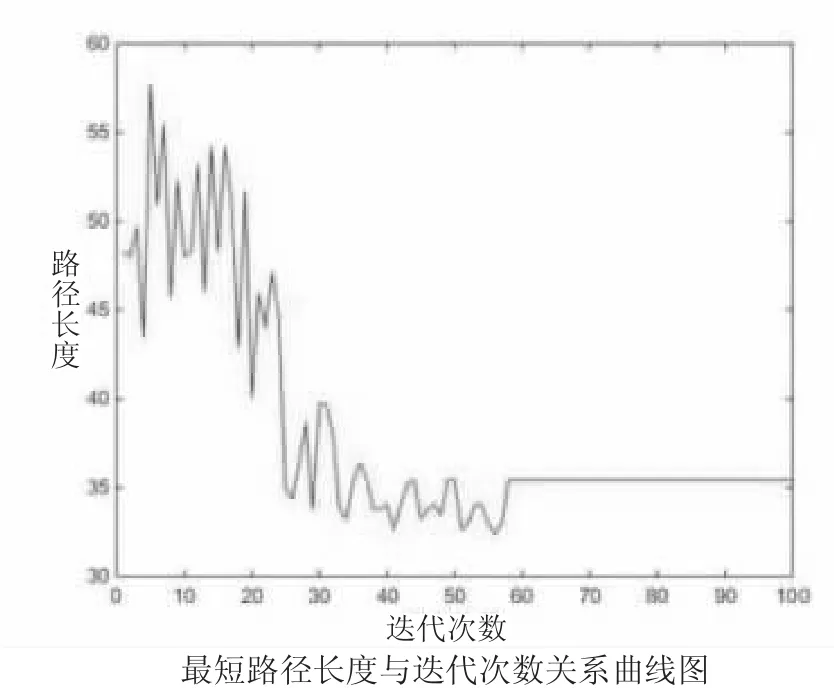
图2 传统蚁群算法路径规划图

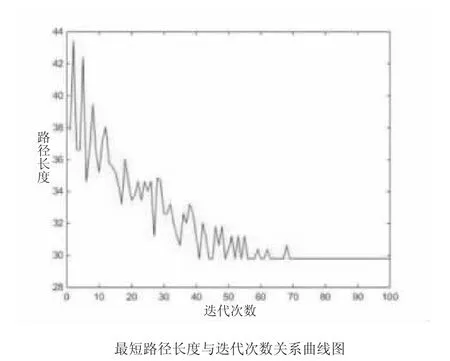
图3 改进蚁群算法路径规划图

由图2 和图3 对比可知，很直观地就能看出改进的蚁群算法是有效果的，改进的蚁群算法明显比传统蚁群算法少走了许多冤枉路，拐弯次数也少了好多次。再由图2 和图3 对比可知，改进蚁群算法所找到的解比传统蚁群算法所找到的解要更优，所找到的最短路径长度比传统的要短11.2%。所用的迭代次数也比传统蚁群算法要少。传统蚁群算法与改进蚁群算法对比数据如表1 所示。

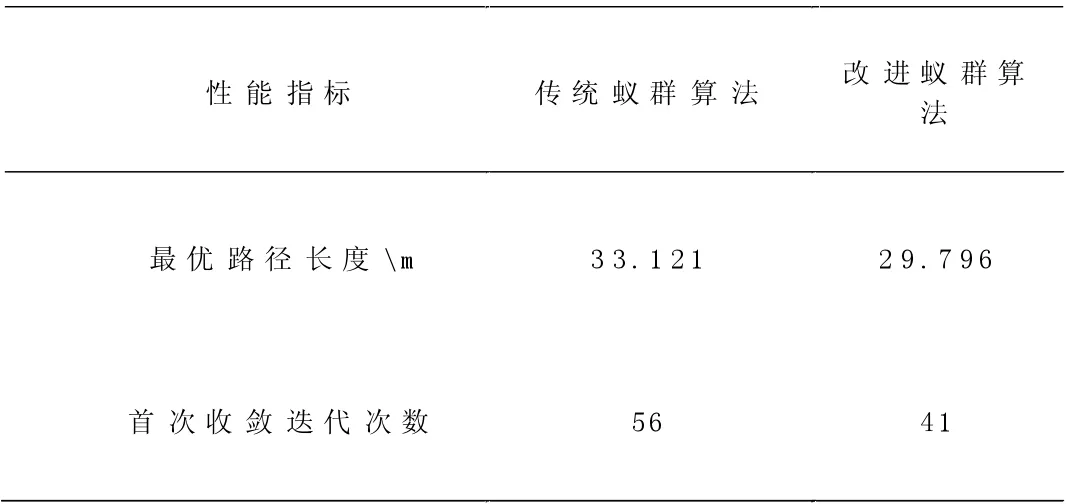
表1 传统蚁群算法与改进蚁群算法性能指标数据对比

4 结论

传统蚁群算法确实存在容易陷入局部最优解、无法找到最优路径的问题，基于此问题，设计了一种自适应信息素挥发因子与舍弃锁死蚂蚁路径信息素但不舍弃蚂蚁的方法处理陷入U型障碍锁死的问题。通过仿真证明改进蚁群算法可以很好地使蚁群避免陷入局部最优解而且能减少迭代次数，提高算法的效率，效果优于传统蚁群算法。