基于ESO的小型飞行器增量动态逆控制律设计

高少婷

(中国飞行试验研究院，西安 710089)

0 引言

随着低成本、轻便型微处理器和惯性测量元件广泛使用，小型飞行器也越来越受到欢迎。

对于小型飞行器来说，由于传感器的约束，获取准确的模型要付出很大的代价、甚至是不可能的，并且往往具有较强的非线性特性。所以，小型飞行器的控制系统必须在提供强鲁棒性的同时能够解决它的非线性问题。文献[1]通过将神经网络与动态逆方法相结合，从而克服动态逆方法对精确模型的依赖性。文献[2]在采用动态逆方法的基础上，利用自适应方法对建模误差进行补偿。但是这些方法多是将动态逆方法与智能控制理论或自适应控制理论相结合，设计过程复杂。文献[3]提出了基于角加速度反馈的动态逆控制方法，该方法将飞行器的控制方程写成增量的形式，以角加速度作为控制反馈，舵面偏转增量作为控制量，降低了控制器对系统模型的依赖性。文献[4]提出了带有跟踪微分器的增量动态逆控制律设计方法，通过跟踪微分器得到状态速率信息。文献[5]通过在控制器中引入预测滤波器，实现对角加速度的滤波和预测。

文中首先建立了小型飞行器的纵向平面的非线性模型，然后设计增量动态逆姿态控制器，引入扩张状态观测器得到控制器所需的状态速率，解决了状态速率难以测量的问题。最后通过MATLAB/Simulink仿真验证控制器的性能。

1 模型描述

采用某小型飞行器模型进行仿真计算，姿态动力学方程如式(1)所示。

(1)

姿态运动学方程如式(2)所示。

(2)

其中，ϑ,ψ,γ为飞行器在空间飞行时的俯仰角、偏航角和滚转角。

2 增量动态逆控制

为了方便描述增量动态逆控制，考虑如下仿射非线性系统:

(3)

式中:x为n维状态向量;控制输入u和系统输出y皆为m维向量;f和h分别为n阶和m阶矩阵;g为一个n×m的控制矩阵。

在(x0，u0)的某个领域内对上述系统进行一阶泰勒展开，即

(4)

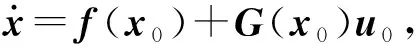
(5)

当控制器采样频率很高，控制计算的周期足够小时，假设控制输入u的变化速率快于状态变量x。考虑到这项因素，最终可化简为:

(6)

则系统输出的动态方程可写为:

(7)

(8)

在实际应用中，采用式(9)。

v=K(yc-y)

(9)

其中yc为系统的期望输出;y为系统的实际输出;K为待设计的系统带宽。

3 小型飞行器增量动态逆控制算法设计

3.1 姿态回路增量动态逆控制

依据动力学模型，基于增量动态逆控制算法对小型飞行器的姿态回路设计控制器，将式(1)写成状态方程的形式：

(10)

其中，将飞行器所受合外力矩分解为两个部分：1)由飞行器的空气动力系数和飞行状态所产生的力矩Ma；2)由执行机构舵面所产生的控制力矩Mc。将系统的姿态控制方程(10)写成如式(3)所示的形式，即

(11)

由式(11)求得姿态回路的控制输入增量形式为:

(12)

v=K2(ωc-ω)

(13)

式中，K2为角速度控制回路带宽。

小型飞行器角回路采用线性控制器，表达式为:

ωc=K1(φc-φ)

(14)

具体的姿态控制回路的结构如图1所示。

图1 小型飞行器姿态控制结构图

3.2 鲁棒性分析及控制参数设计

由于小型飞行器动力学模型存在不确定性和未建模动态，所以需要分析所设计控制器的鲁棒性。

(15)

依据前文所述，系统方程可简化为:

(16)

将增量动态逆控制律代入式(16)，可得

(17)

对于小型飞行器姿态角速度回路来说，式(17)可写为:

(18)

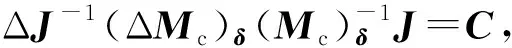
(19)

由此可以得到角速度控制回路的闭环系统结构如图2所示，通过计算得到角速度回路的相应闭环传递函数如式(20)，从中可以看出，系统中的不确定性被消除。

图2 小型飞行器角速度闭环结构框图

(20)

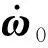
（1984年1月6日讲座，全文略有删节。吴培华教授提供讲座录音，史悠整理，刘祥安教授审阅，在此特申谢忱！）

以俯仰角控制为例，研究控制参数的设计。由式(21)可知俯仰角速度回路闭环传函为k2/(k2+s)，因此简化后的俯仰角控制回路的闭环系统结构图如图3所示。

图3 小型飞行器俯仰姿态闭环结构框图

在此基础上，对于俯仰角控制系统的整个闭环回路传递函数可表示为：

(21)

标准的二阶系统传递函数形式为:

(22)

因此，可以得到下面的表达式:

(23)

为使系统具有较好的闭环特性，取ξ=1，ωn=20，由此计算得到:

k1=10,k2=40

(24)

3.3 角加速度的获取

通过陀螺仪测量可以得到飞行器的角速度，若是通过微分的方式得到角加速度，则获得的角加速度信息噪声过大，所以文中提出了一种通过扩张状态观测器估计角加速度信息的方法。具体形式为：

(25)

式中:z1为对角速度的估计值;z2为对角加速度的估计值;βi为观测器的控制系数。其中非线性函数fal表达式为：

(26)

4 仿真结果与分析

由文中所设计的增量式动态逆控制器和小型飞行器纵向动力学模型，在MATLAB仿真环境验证所设计的控制系统的性能。要求飞行器作无侧滑无倾斜的运动。初始状态为：俯仰角ϑ=0°，速度V=25 m/s。对控制参数进行设计，增量动态逆控制器的设计参数为：k1=10,k2=40；扩张状态观测器控制参数为λ=0.5，α=0.5，β1=200，β2=300；输入指令周期为4 s，0°～5°为跳变的俯仰角指令，仿真结果如图4所示。

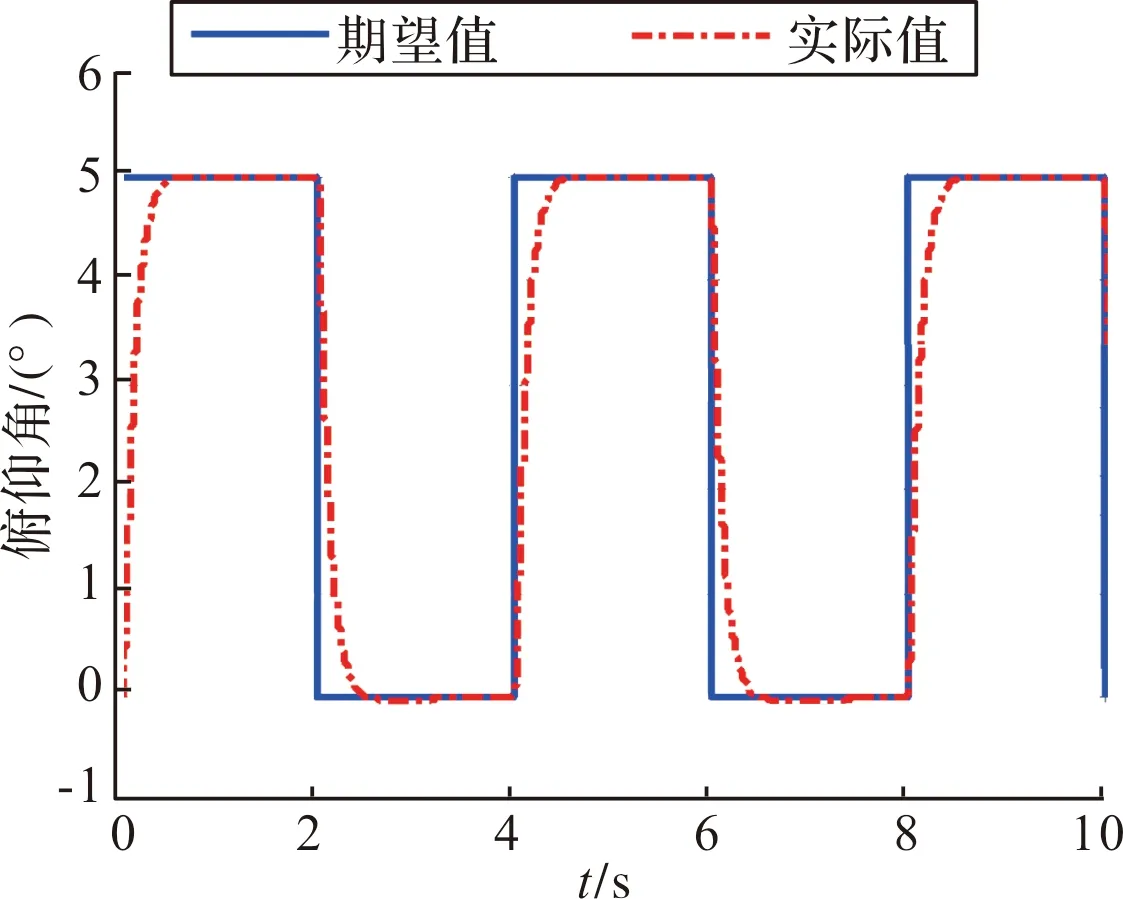
图4 俯仰角跟踪曲线

从以上仿真结果可以看出，在无摄动无干扰的情况下，系统的响应时间约为0.4 s，响应较快，具有很好的快速性，几乎无超调，具有良好的控制效果，证明所设计的的增量动态逆控制能够实现小型飞行器的姿态控制，且动态性能良好。

因为小型飞行器的气动参数具有不确定性，为验证所设计控制器的鲁棒性，在仿真中将气动参数拉偏30%，观察参数摄动影响下控制器的性能效果。

图5 气动参数拉偏30%俯仰角跟踪曲线

由图5可知，在加入气动参数摄动之后控制器仍能实现小型飞行器的姿态稳定跟踪，并且具有良好的快速性，从而验证了控制系统的鲁棒性。

5 结论

针对小型飞行器气动参数不确定性的问题，设计了基于扩张状态观测器的增量动态逆控制方法。通过角加速度的引入降低了控制系统对飞行器气动参数不确定性的敏感度。通过扩张状态观测器实时估计角加速度信息，解决了角加速度无法直接测量的困难。仿真结果表明，当飞行器精确模型难以建立，存在参数摄动时，所设计的方法具有较好的鲁棒性。